二次ベジエ曲線の長さを求める。
quadraticCurveLength
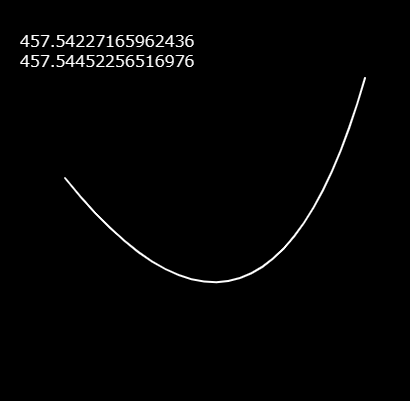
まず、二次ベジエ曲線とは3つのコントロールポイント:
(a_0, b_0, c_0),~~(a_1, b_1, c_1),~~(a_2, b_2, c_2)
により、次のように表される曲線である:
\begin{align*} x &= a_0(1-t)^2 + 2a_1 t(1-t) + a_2t^2, \\[5pt] y &= b_0(1-t)^2 + 2b_1 t(1-t) + b_2t^2, \\[5pt] z &= c_0(1-t)^2 + 2c_1 t(1-t) + c_2t^2. \end{align*}
ただし~t_0\leq t \leq t_1~とする。曲線の長さを与える式を求める。
はじめに、
u_0 = a_0 - a_1,~~~v_0 = b_0-b_1,~~~w_0 = c_0-c_1
とおく。さらに、
u_1 = a_0-2a_1+a_2,~~v_1=b_0-2b_1+b_2,~~w_1=c_0-2c_1+c_2
とおく。そして、
A={u_1}^2 + {v_1}^2 + {w_1}^2,
B=u_1u_0 + v_1v_0 + w_1w_0,
C={u_0}^2 + {v_0}^2 + {w_0}^2,
とおく。シュワルツの不等式より、~D\geq0~がわかる。
このとき、求める曲線の長さは次のようになる。まず補助関数を用意する。
g(x) = \log(x + \sqrt{x^2+1}) + x\sqrt{x^2 + 1}.
曲線の長さ~L~は、まず~A>0~かつ~D>0~のとき、
L = \frac{D}{A\sqrt{A}} \left( g\left( \frac{At_1-B}{\sqrt{D}} \right) - g\left( \frac{At_0-B}{\sqrt{D}} \right) \right).
次に~A>0~かつ~D=0~の場合は、
L = \frac{1}{A\sqrt{A}} \left( (At_1-B)|At_1-B| - (At_0-B)|At_0-B| \right).
最後に~A=0~の場合、~B~も~D~も0になるので、
となる。
以上です。


Discussion