Google CTF Tiramisu write up
概要
このソースコードはprotobufで通信をしています
大まかに、secp224r1で公開鍵を作成→ECDHで鍵交換→AES-CTRで通信といった形になっています。結構真面目な実装で、きちんと鍵交換をしたあとにはhkdfという鍵導出関数が用いられていました。図示するとこんな感じ
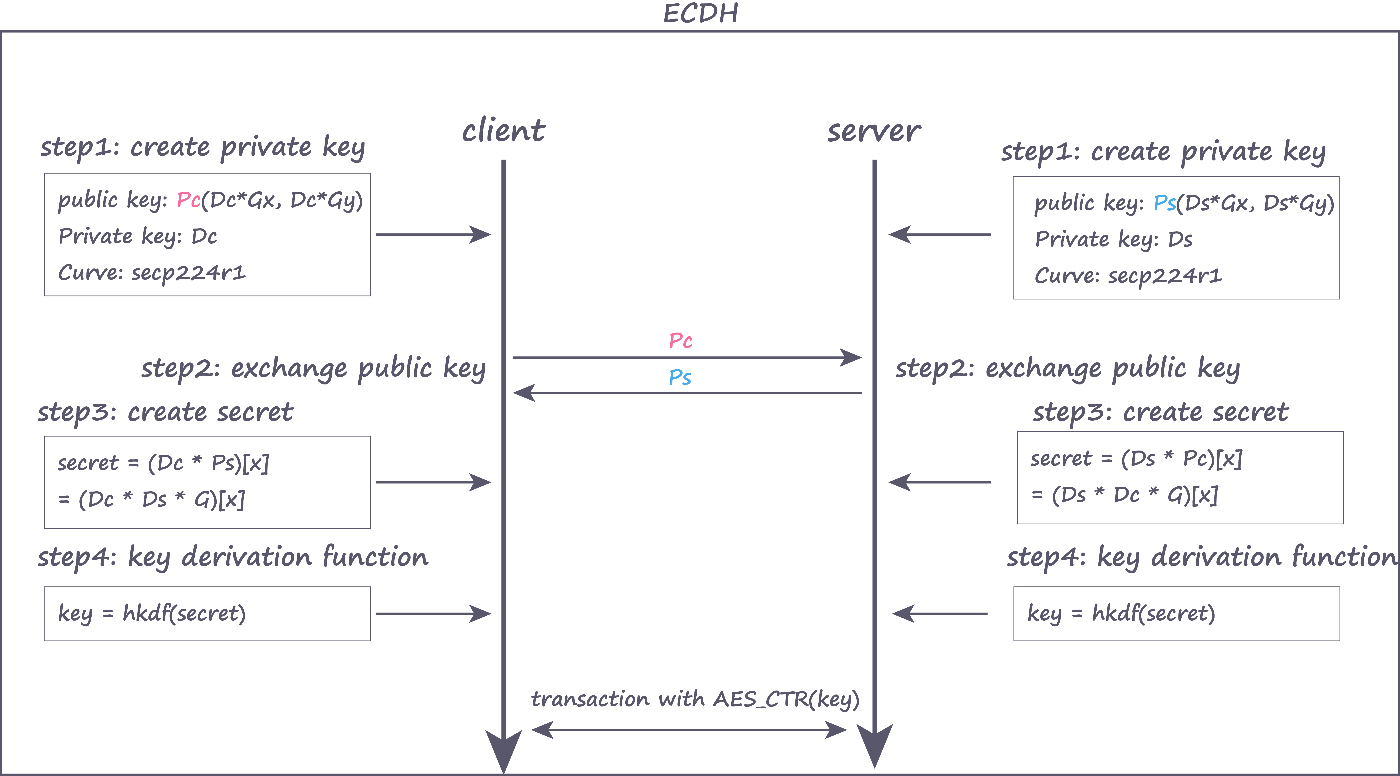
そしてサーバーサイドの秘密鍵 Ds を特定すると、フラグが獲得できるという問題でした。
脆弱性: Invalid Curve Attack
ソースコードを見ていると、一箇所怪しい場所を見つけました。
ここはさっきの図のstep3のお互いの公開鍵を交換する場所です。
peer はクライアントから渡された鍵を表しているのですが、 peer.Curve.IsOnCurve(peer.X, peer.Y) からわかるように、クライアントから渡された曲線の上に乗っているかどうかの確認はしているのですが、どうやらサーバーサイドで生成した曲線の上に乗っているかどうか確認していないようです。つまりクライアントから secp224r1 ではない 曲線の点を与えて、サーバーサイドでその点を使って計算させることができる可能性があるということです。このサーバーでは、 secp224r1 と secp256r1 のみ使用することができるので、最終的にこっちから送る値は secp256r1 になります。
// Key sanity checks.
if !peer.Curve.IsOnCurve(peer.X, peer.Y) {
return fmt.Errorf("point (%X, %X) not on curve", peer.X, peer.Y)
}
fmt.Printf("Curve: %v\n", peer.Curve.Params().P)
// Compute shared secret.
P := server.key.Params().P
D := server.key.D.Bytes()
sharedX, _ := server.key.ScalarMult(new(big.Int).Mod(peer.X, P), new(big.Int).Mod(peer.Y, P), D)
曲線の上に乗っていない点で計算させると、Invalid Curve Attack という攻撃手法に繋がる可能性があります。(https://elliptic-shiho.hatenablog.com/entry/2016/07/20/084509 , https://furutsuki.hatenablog.com/entry/2020/05/05/112207)
この脆弱性を要約すると、 ある特定の点を与えると、位数が激下がりしてしまうといったものです。
実際にsecp224r1で位数が激下がりする点を見てみましょう。
以下のファイルで、与えた座標を1倍,2倍,と増やしていくと、何が起きるのか観察してみましょう
package main
import (
"crypto/elliptic"
"fmt"
"math/big"
)
func main() {
e224 := elliptic.P224()
P := e224.Params().P
x, _ := new(big.Int).SetString("8825082724693141710766634404968356130117611599944641380068285935075", 10)
y, _ := new(big.Int).SetString("1539798741935464936044776598857897570091336976431935576877461275012", 10)
e256 := elliptic.P256()
fmt.Printf("%v\n", e256.IsOnCurve(x, y))
for i := int64(0); i < 20000; i++ {
mody := new(big.Int).Mod(y, P)
D := big.NewInt(i)
sharedX, sharedY := e224.ScalarMult(x, mody, D.Bytes())
fmt.Printf("%v, %v\n", sharedX, sharedY)
}
}
実行結果
false
0, 0
8825082724693141710766634404968356130117611599944641380068285935075, 1539798741935464936044776598857897570091336976431935576877461275012
8825082724693141710766634404968356130117611599944641380068285935075, 25420147925215174858622238488161733103466579283594372566632605023869
0, 0
8825082724693141710766634404968356130117611599944641380068285935075, 1539798741935464936044776598857897570091336976431935576877461275012
8825082724693141710766634404968356130117611599944641380068285935075, 25420147925215174858622238488161733103466579283594372566632605023869
先頭のfalseは secp256r1 の曲線に乗っていないよということを表しています。今回の攻撃条件の制約上、こちらは載せなければならないのでここは最終的に true にする必要があります。 しかし、今の段階でも位数は確実に下がっています。3回で一巡してしまっています。
なので、サーバー側でこの点とDを掛け算してしまうと、3通りの値しか計算結果が出ないということになります。
なぜこのようになってしまうのでしょうか? それは楕円曲線暗号の式を見ればヒントがあります。https://ja.wikipedia.org/wiki/楕円曲線暗号 加算、2倍の計算の式を見てもらえるとわかると思うのですが、これらの式に b が出てこないのです。bが出てこないので、実は b は 点 で与えられる情報であって、それ以降は関係ないんですね。つまり、 b をずらした曲線の点を与えると、ずーっと b がずれたままになっちゃいます。 b がずれるとどうなるかというと、位数が低い素因数を持つ可能性があります。例えば位数が2で割り切れたとしましょう。この場合、位数が 2*X の形で表せられるようになると思うのですが、このときにベースポイントをGとして、 (XG) という点をこの曲線に与えると、2*(XG) = 0 -> 3*(GX) = XG というふうに二回ずつでループしてしまいます。これが位数が低くなるメカニズムです。小さな素因数を持つ曲線の生成方法としては、パラメータの
このX座標を使って、鍵導出を行うので、サーバー側のXの値が予測できたときのみ、うまく通信ができる(つまり暗号化や復号が成立し、まともな通信ができる)ということになります。しかし見ての通り、実はyの値は違っていてもの値が同じになってしまうケースが必ず2つずつ存在します。これは楕円曲線暗号のN倍の計算の都合上、かならずyがひっくり返った値があるからですね。
逆に、「うまく通信ができたときは予測が成功したときだ」。ということにもなるので、この事実を使って情報を集めていくことになります。結果、D mod N[i] でいろんな情報を集めることができるので、中国剰余定理でDを復元できるというメカニズムです。
しかし、
- xの値の候補が1回あたりの試行で必ず2つずつ出てきてしまうという問題
- secp256r1上に乗せなければならない
という2つの問題は未だ顕在です。
xの値の候補が1回あたりの試行で必ず2つずつ出てきてしまうという問題
これはどうあがいても避けられません。ここで、Dのbit数を確認してみましょう。
secp224r1は https://neuromancer.sk/std/secg/secp224r1/ こちらの値を引用すると、
n = 0xffffffffffffffffffffffffffff16a2e0b8f03e13dd29455c5c2a3d
となっています。こちら 224bit になっているので、中国剰余定理で復元するためには mod N[i] の N[i] の積が224bit以上にならなければなりません。 N[i] が1000程度の素数であれば、22個程度の情報が集まれば復元可能になります。一個あたり2つの候補があったとしても、これらを総当りするには 2^22 = 10^6程度 試せば良いので、こちらは十分総当り可能です。なのでこちらの問題はクリアできました。ちなみに1回あたりのリクエストが1秒程度なので、 mod 1000 の情報 を得るためには500秒程度の情報が必要です(ひとつあたりの候補が2つ出てくるので、実質半分です)。それが22個必要なので500*22=11000秒 = 183分 = 3時間程度かかります。この間に他の作業ができる人はいいですが、急ぎの人は並列で回して高速化したほうが良いでしょう。22並列だと500秒程度=5分以内で終わります。
secp256r1に載せないといけない問題。
こちらのほうが問題です。 secp224r1 の位数が低くなる点であり、さらに secp256r1 の点でなければなりません。こちらは少し式変形して考えてみます。 secp256r1 で満たさなければならない式が以下だったとします。(各パラメータはsecp256r1に準拠します。)
位数が低い点がこの曲線に乗ってなければならないということは、この式が渡したい(位数が低くなる)点で成立していなければならないということです。ここで、 mod p に注目すると、
そして mod の sqrt は Tonelli-Shanks algorithm というアルゴリズムで計算可能です。よって、計算結果を
となります。そして、 secp224r1 の p とすると
これは中国剰余定理などで求めればよいでしょう。自分は思いつかなかったので雑に拡張ユークリッドの互除法で求めています。
from sage.all import *
import sys
A = 0xfffffffffffffffffffffffffffffffefffffffffffffffffffffffe
B = 0xb4050a850c04b3abf54132565044b0b7d7bfd8ba270b39432355ffb4
P = 0xffffffffffffffffffffffffffffffff000000000000000000000001
F = GF(P)
size = EllipticCurve(F, [A, B]).order()
def make_xy(xy):
# Finite field prime
p256 = 0xFFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFF
# Curve parameters for the curve equation: y^2 = x^3 + a256*x +b256
a256 = p256 - 3
b256 = 0x5AC635D8AA3A93E7B3EBBD55769886BC651D06B0CC53B0F63BCE3C3E27D2604B
# Base point (x, y)
gx = 0x6B17D1F2E12C4247F8BCE6E563A440F277037D812DEB33A0F4A13945D898C296
gy = 0x4FE342E2FE1A7F9B8EE7EB4A7C0F9E162BCE33576B315ECECBB6406837BF51F5
# Curve order
qq = 0xFFFFFFFF00000000FFFFFFFFFFFFFFFFBCE6FAADA7179E84F3B9CAC2FC632551
FF = GF(p256)
# Define a curve over that field with specified Weierstrass a and b parameters
EC = EllipticCurve([FF(a256), FF(b256)])
# Since we know P-256's order we can skip computing it and set it explicitly
EC.set_order(qq)
# Create a variable for the base point
G = EC(FF(gx), FF(gy))
p224 = 0xffffffffffffffffffffffffffffffff000000000000000000000001
a224 = 0xfffffffffffffffffffffffffffffffefffffffffffffffffffffffe
x = xy[0]
y = xy[1]
yy = ZZ(mod(x^3 + a256 * x + b256, p256).sqrt() % p256)
d,u,v = xgcd(p224, p256)
assert p224 * u + p256 * v == d
u = u * (yy-y)
v = -v * (yy-y)
ans = yy + p256 * v
if ans < 0:
ans += (-ans // p256*p224) * p256*p224*2
return x, ans
nums = set()
primes = set()
for i in range(2,100):
if i in Primes():
primes.add(i)
cur = 1
b = 2
while cur < size:
b += 1
EC = EllipticCurve(F, [A, b])
order = EC.order()
suborder = -1
for i in primes:
if order % i == 0 and not i in nums:
suborder = i
if suborder == -1:
continue
g = EC.gen(0) * int(order // suborder)
print(g.xy())
try:
x, y = make_xy((ZZ(g.xy()[0]), ZZ(g.xy()[1])))
except:
continue
xs = []
for i in range(suborder+1):
try:
num = (i * g).xy()
xs.append(num[0])
except:
xs.append(0)
try:
print({
"x": x,
"y": y,
"order": suborder,
"b": b,
"xs": xs
}, ",")
except:
continue
nums.add(suborder)
cur *= suborder
print((cur/size).n(), file=sys.stderr, flush=True)
フラグ獲得まで
さあこれで準備は整いました。あとはこの点をサーバーに渡して、複合してもらうだけです。
modの情報を集めるソースコード
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# Copyright 2020 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import argparse
import pwnlib
import pwnlib.tubes
from pwnlib.util.packing import signed
import challenge_pb2
import struct
import sys
from Crypto.Util.number import long_to_bytes
from candidate_list import candidate_list
import time
from cryptography.hazmat.primitives import hashes, hmac
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from cryptography.hazmat.primitives.asymmetric import ec
CHANNEL_CIPHER_KDF_INFO = b"Channel Cipher v1.0"
CHANNEL_MAC_KDF_INFO = b"Channel MAC v1.0"
secrets = []
IV = b'\x00\x11\x22\x33\x44\x55\x66\x77\x88\x99\xaa\xbb\xcc\xdd\xee\xff'
class AuthCipher(object):
def __init__(self, secret, cipher_info, mac_info):
self.cipher_key = self.derive_key(secret, cipher_info)
self.mac_key = self.derive_key(secret, mac_info)
def derive_key(self, secret, info):
hkdf = HKDF(
algorithm=hashes.SHA256(),
length=16,
salt=None,
info=info,
)
return hkdf.derive(secret)
def encrypt(self, iv, plaintext):
cipher = Cipher(algorithms.AES(self.cipher_key), modes.CTR(iv))
encryptor = cipher.encryptor()
ct = encryptor.update(plaintext) + encryptor.finalize()
h = hmac.HMAC(self.mac_key, hashes.SHA256())
h.update(iv)
h.update(ct)
mac = h.finalize()
out = challenge_pb2.Ciphertext()
out.iv = iv
out.data = ct
out.mac = mac
return out
def decrypt(self, iv, plaintext):
cipher = Cipher(algorithms.AES(self.cipher_key), modes.CTR(iv))
decryptor = cipher.decryptor()
ct = decryptor.update(plaintext)
return ct == b'hello'
def handle_pow(tube):
raise NotImplemented()
def read_message(tube, typ):
n = struct.unpack('<L', tube.recvnb(4))[0]
buf = tube.recvnb(n)
msg = typ()
msg.ParseFromString(buf)
return msg
def write_message(tube, msg):
buf = msg.SerializeToString()
tube.send(struct.pack('<L', len(buf)))
tube.send(buf)
def curve2proto(c):
assert(c.name == 'secp224r1')
return challenge_pb2.EcdhKey.CurveID.SECP224R1
def key2proto(key):
assert(isinstance(key, ec.EllipticCurvePublicKey))
out = challenge_pb2.EcdhKey()
out.curve = curve2proto(key.curve)
x, y = key.public_numbers().x, key.public_numbers().y
out.public.x = x.to_bytes((x.bit_length() + 7) // 8, 'big')
out.public.y = y.to_bytes((y.bit_length() + 7) // 8, 'big')
return out
def proto2key(key):
assert(isinstance(key, challenge_pb2.EcdhKey))
assert(key.curve == challenge_pb2.EcdhKey.CurveID.SECP224R1)
curve = ec.SECP224R1()
x = int.from_bytes(key.public.x, 'big')
y = int.from_bytes(key.public.y, 'big')
public = ec.EllipticCurvePublicNumbers(x, y, curve)
return ec.EllipticCurvePublicKey.from_encoded_point(curve, public.encode_point())
def run_session(port, key_index, local, index):
secrets = list(map(lambda x: long_to_bytes(x), candidate_list[index]["xs"]))
if local:
tube = pwnlib.tubes.remote.remote('127.0.0.1', port)
else:
tube = pwnlib.tubes.remote.remote('tiramisu.2021.ctfcompetition.com', port)
# TODO: onにする
print(tube.recvuntil('== proof-of-work: '), file=sys.stderr)
if tube.recvline().startswith(b'enabled'):
handle_pow()
server_hello = read_message(tube, challenge_pb2.ServerHello)
server_key = proto2key(server_hello.key)
# print("=== server_hello ===")
# print(server_hello)
private_key = ec.generate_private_key(ec.SECP224R1())
client_hello = challenge_pb2.ClientHello()
client_hello.key.CopyFrom(key2proto(private_key.public_key()))
client_hello.key.curve = challenge_pb2.EcdhKey.CurveID.SECP256R1
client_hello.key.public.x = long_to_bytes(candidate_list[index]['x'])
client_hello.key.public.y = long_to_bytes(candidate_list[index]['y'])
# print("=== client_hello ===")
# print(client_hello)
write_message(tube, client_hello)
shared_key = private_key.exchange(ec.ECDH(), server_key)
shared_key = secrets[key_index]
# print("=== shared_key ===")
# print(shared_key)
channel = AuthCipher(shared_key, CHANNEL_CIPHER_KDF_INFO, CHANNEL_MAC_KDF_INFO)
msg = challenge_pb2.SessionMessage()
msg.encrypted_data.CopyFrom(channel.encrypt(IV, b'hello'))
write_message(tube, msg)
# print('msg:', msg)
reply = read_message(tube, challenge_pb2.SessionMessage)
tube.close()
# print('reply:', reply)
try:
return channel.decrypt(reply.encrypted_data.iv, reply.encrypted_data.data)
except:
return False
def main():
parser = argparse.ArgumentParser()
parser.add_argument('--port', metavar='P', type=int, default=1337, help='challenge #port')
parser.add_argument('--local', metavar='L', type=bool, default=False, help='secret number')
parser.add_argument('--index', metavar='I', type=int, default=False, help='secret number')
args = parser.parse_args()
index = args.index
for i in range(candidate_list[index]['order']):
print("log:", index, "/", len(candidate_list) , ":", i, "/", candidate_list[index]['order'], file=sys.stderr)
while True:
try:
if run_session(args.port, i, args.local, index):
num = []
for j in range(len(candidate_list[index]['xs'])):
if candidate_list[index]['xs'][j] == candidate_list[index]['xs'][i]:
num.append(j)
return {"mod": candidate_list[index]['order'], "values": num}
break
except pwnlib.exception.PwnlibException:
continue
return 0
if __name__ == '__main__':
print(main())
総当りで中国剰余定理で復号するコード
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# Copyright 2020 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import pwnlib.tubes
from Crypto.Util.number import bytes_to_long
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from sage.misc.prandom import expovariate
import sys
class AuthCipher(object):
def __init__(self, secret, cipher_info, mac_info):
self.cipher_key = self.derive_key(secret, cipher_info)
self.mac_key = self.derive_key(secret, mac_info)
def derive_key(self, secret, info):
hkdf = HKDF(
algorithm=hashes.SHA256(),
length=16,
salt=None,
info=info,
)
return hkdf.derive(secret)
def decrypt(self, iv, plaintext):
cipher = Cipher(algorithms.AES(self.cipher_key), modes.CTR(iv))
decryptor = cipher.decryptor()
ct = decryptor.update(plaintext)
return ct
nums = [
{'mod': 1697, 'values': [20, 1677]},
{'mod': 1579, 'values': [10, 1569]},
{'mod': 2659, 'values': [51, 2608]},
{'mod': 1361, 'values': [262, 1099]},
{'mod': 2593, 'values': [269, 2324]},
{'mod': 1213, 'values': [505, 708]},
{'mod': 3019, 'values': [21, 2998]},
{'mod': 1069, 'values': [309, 760]},
{'mod': 8513, 'values': [2921, 5592]},
{'mod': 1699, 'values': [185, 1514]},
{'mod': 9631, 'values': [4614, 5017]},
{'mod': 1193, 'values': [547, 646]},
{'mod': 1283, 'values': [497, 786]},
{'mod': 2029, 'values': [477, 1552]},
{'mod': 1277, 'values': [131, 1146]},
{'mod': 1103, 'values': [421, 682]},
{'mod': 5807, 'values': [1148, 4659]},
{'mod': 6691, 'values': [1545, 5146]},
{'mod': 1459, 'values': [528, 931]},
{'mod': 2473, 'values': [350, 2123]},
{'mod': 4483, 'values': [1130, 3353]},
]
for i in range(1 << len(nums)):
print(i, "/", 1<<len(nums), file=sys.stderr)
values = []
mods = []
for j in range(len(nums)):
values.append(nums[j]['values'][(i >> j)&1])
mods.append(nums[j]['mod'])
try:
shared_key = int(crt(values, mods)).to_bytes(224//8, byteorder='big')
except:
continue
iv = b"s@v\325g\340\t*\274\341\t\025\202UC}"
data = b">}\"B\352\"WgA\234*\014p\326b\\O6\374\250\217K\343\334U\374\252~\267\026\325\212J\3178M\354{q\231\201\310\351yyj`3_\224^\313\204P\200\323\233="
flagCipherKdfInfo = b"Flag Cipher v1.0"
flagMacKdfInfo = b"Flag MAC v1.0"
channel = AuthCipher(shared_key, flagCipherKdfInfo, flagMacKdfInfo)
print(channel.decrypt(iv, data))
CTFでgrepするとフラグが見つかります🧙
感想
Invalid Curve Attackを知らなかったので、とてもいい勉強になりました。ググっていると、たしかにn倍するときにb出てこないね!!!!となりました。すごい!えらい!
この問題、ほとんどできていたのですが当日体力がなくなってしまい、とけずじまいでした。重そうな問題ははじめから真面目なコードで書くべきですね。
また機会があれば動画にしようと思いますそれではまた!
追記
二乗にして、あとからsqrtする手段を教えてもらいました。天才です。

Discussion