Pythonデータ分析・可視化ことはじめ
ここのところずっと
- pandas
- Streamlit
- Plotly
あたりをずっと触ってるけど、記録残してなくてどんどん進めちゃって後で困りそうなので、ちゃんと記録を残していく
回帰分析
回帰分析とは?
- 求めたい結果(「目的変数」という)
- 結果に対して何らかの影響を与える要素(「説明変数」という)
- 求めたい結果に対して、何らかの要素が、どの程度影響を与えるかを分析する手法
回帰分析の種類
- 単回帰分析
- 要素が1つ
- 重回帰分析
- 要素が複数
例
- 店舗の売上に対して、席数がどのように影響を与えるか?
- 店舗の売上に対して、駅との距離がどのように影響を与えるか?
- 店舗の売上に対して、気温がどのように影響を与えるか?
みたいな切り口が1つの場合。
Googleスプレッドシートを使った単回帰分析
まずはスプレッドシートを使った単回帰分析から。
参考)https://data-viz-lab.com/regression-analysis
- 以下のようなシートを作る
- 説明変数を左、目的変数を右にすると良いらしい
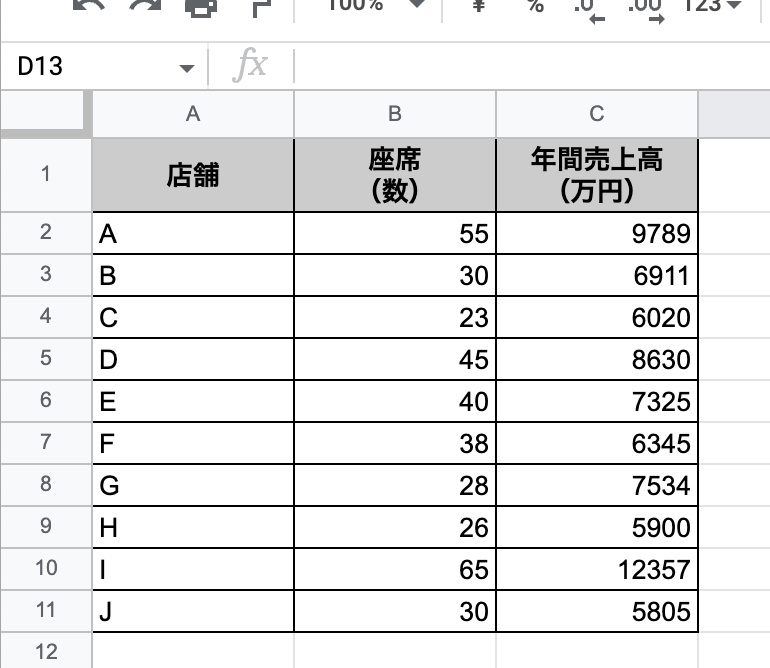
- 説明変数と目的変数の列を選択する

- グラフを作成する
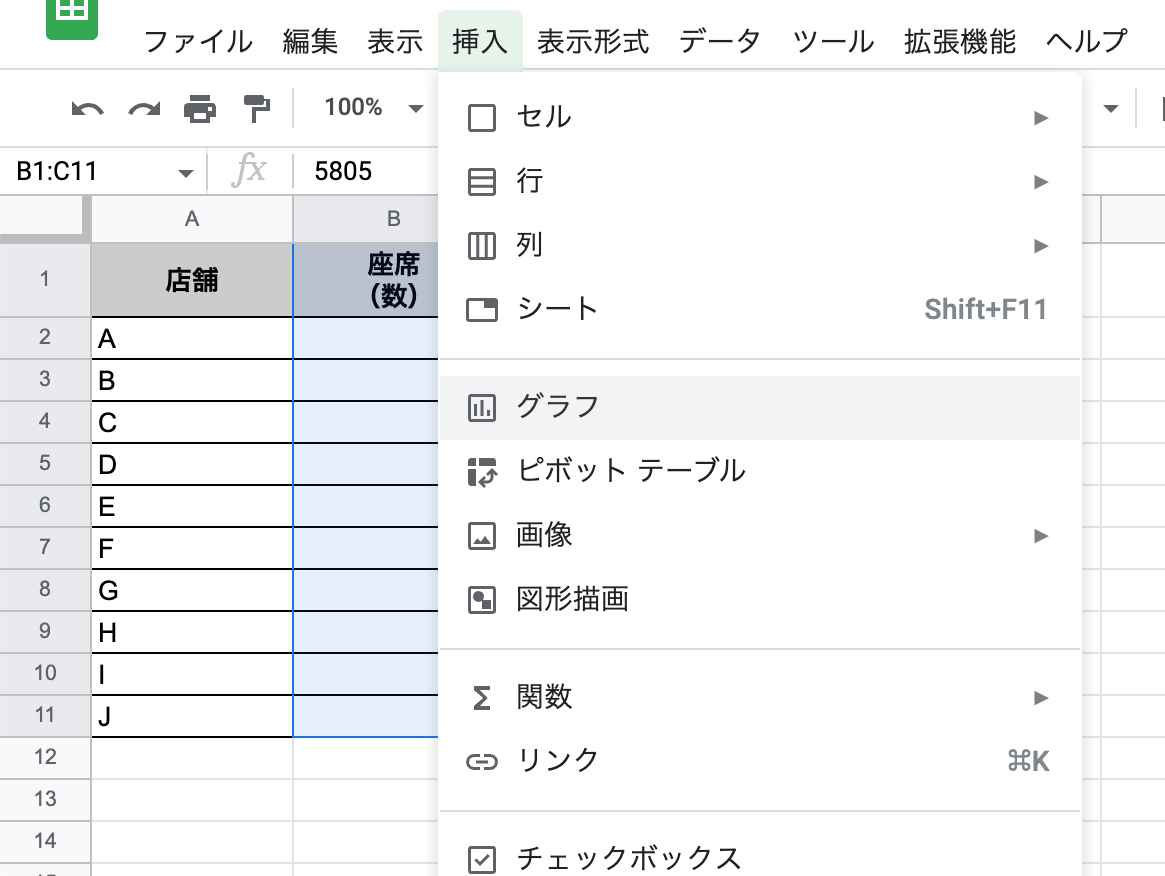
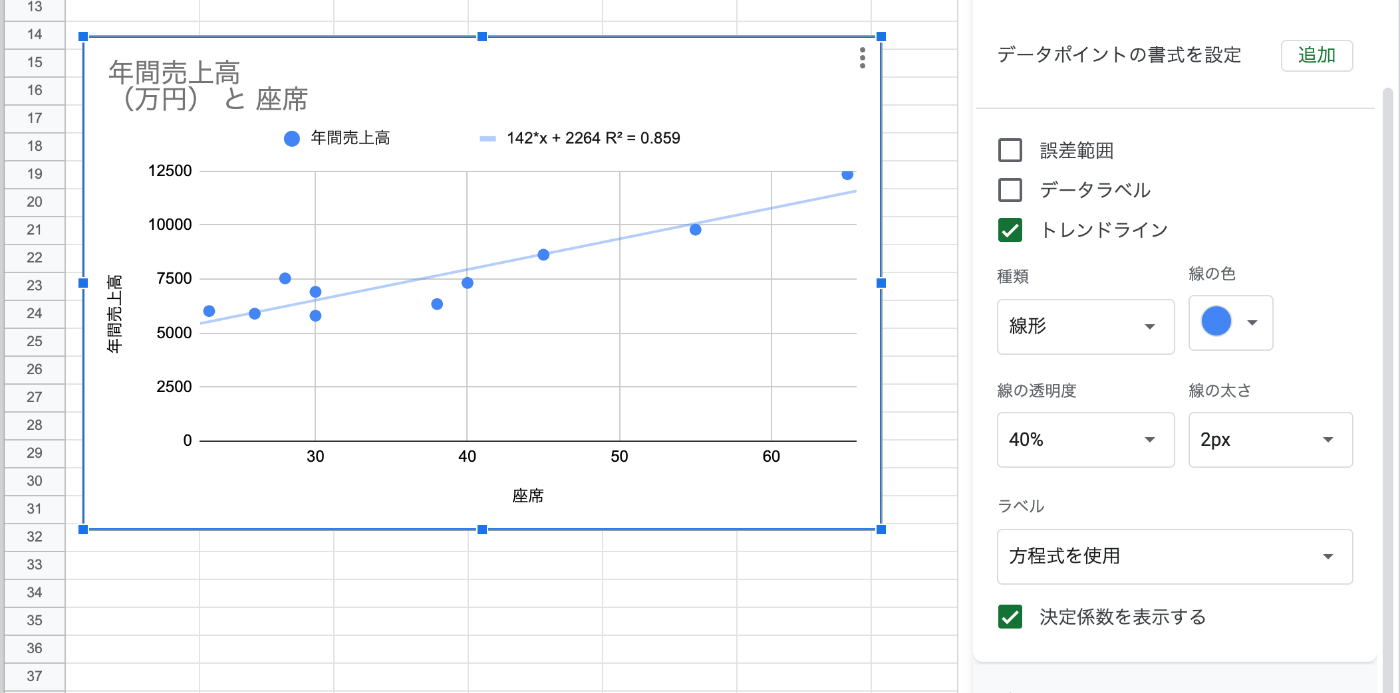
- グラフが作成されたが、必要なのは折れ線グラフではなく散布図。ということで、グラフタイプを散布図に変更する

- 散布図に切り替わった。
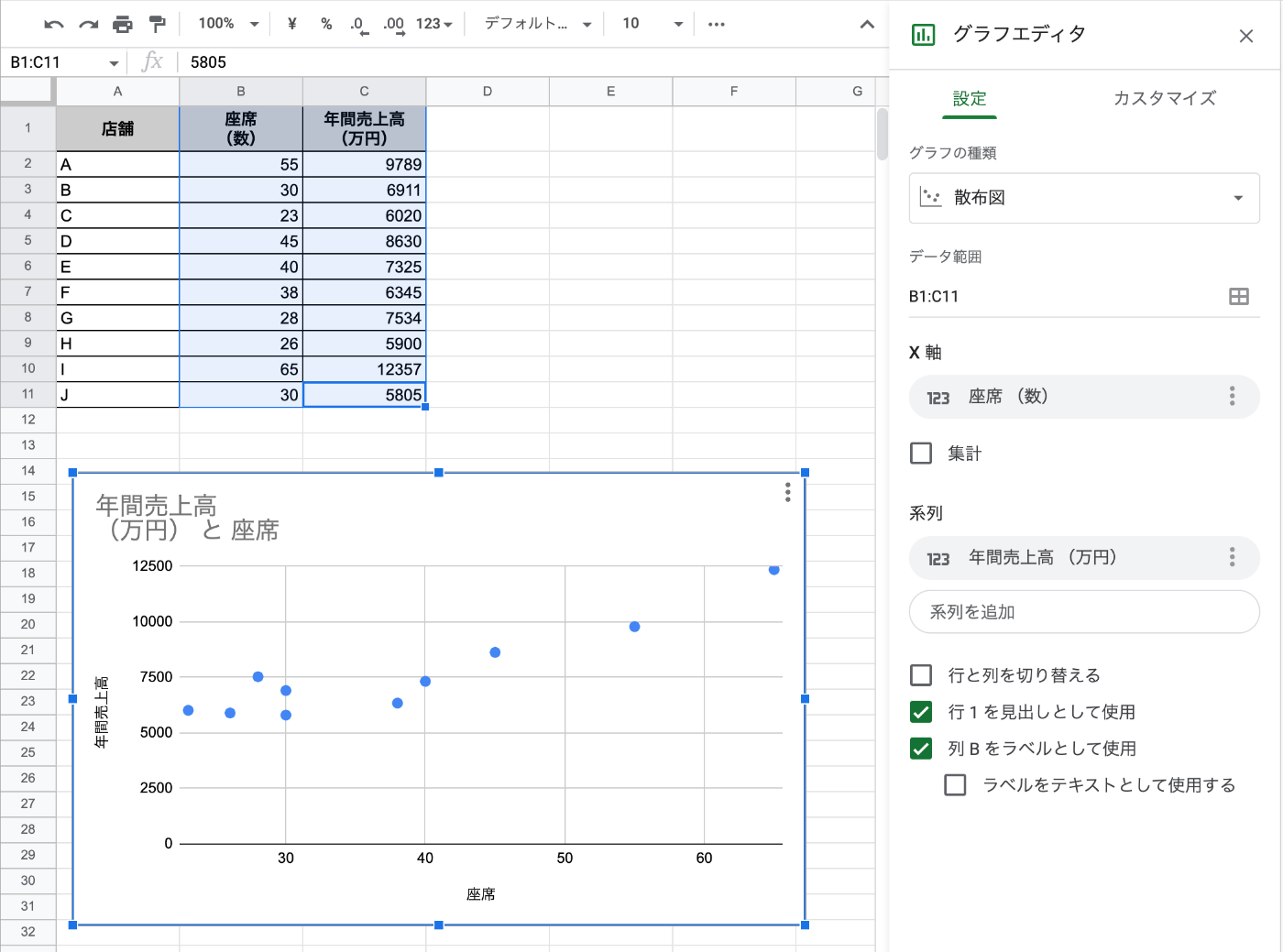
- さらにカスタマイズ→系列→トレンドラインにチェックを入れると回帰直線が自動で引かれる

- さらに少し下にあるラベルで「方程式を使用」を選択すると回帰式が得られる

- さらに「決定係数を表示する」にチェックを入れるとR2乗=決定係数が得られる
Pandas/skicit-learnを使った単回帰分析
同じことをpandas/matplotlib/skicit-learnでやってみる。表示はstreamlit。
参考)https://qiita.com/karaage0703/items/701367b6c926552fe505
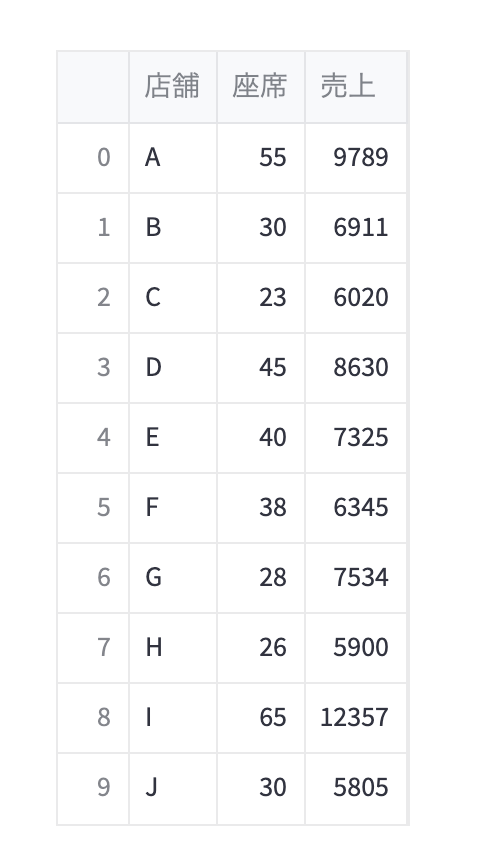
pandasでデータフレーム作成
import pandas as pd
df = pd.DataFrame(
data={
"座席": [55, 30, 23, 45, 40, 38, 28, 26, 65, 30],
"売上": [9789, 6911, 6020, 8630, 7325, 6345, 7534, 5900, 12357, 5805],
}
)
df
説明変数と目的変数を取り出す。df[[列名]]でDataframeとして出力される。
x = df[["座席"]]
y = df[["売上"]]
matplotlibでグラフ作成
import matplotlib.pyplot as plt
import streamlit as st
fig = plt.figure()
plt.plot(x, y, "o")
st.pyplot(fig)

単回帰分析を行うために、scikit-learnで学習させる。
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x,y)
回帰直線を引く。
plt.plot(x, model.predict(x), linestyle="solid")
st.pyplot(fig)

回帰式とR2を出力する
st.text("y = %.2fx + %.2f" % (model.coef_, model.intercept_))
st.text("R2 = %.2f" % model.score(x, y))
y = 142.05x + 2263.60
R2 = 0.86
単回帰分析まとめ
参考)https://data-viz-lab.com/regression-analysis
単回帰分析は以下の公式となる。
- Y: 目的変数
- X: 説明変数
- a: 回帰係数/傾き
- b: 切片
今回の例だとこうなる
回帰係数は、座席が1増えたときの売上予測となる。今回の場合だと座席が増えると142.05万円増えると予測される。
切片は回帰係数が0の場合の売上となるが実際にはありえない。1次関数でy軸と交差するところだと考えればよい。
参考)http://kentiku-kouzou.jp/suugaku-seppen.html
R2は決定係数とも呼ばれる。以下の公式で求められる(らしい、数学わからん・・・)
R2は、端的に言ってしまうと分析結果の信頼度。データが以下に回帰直線に収まりよく並んでいるかを示している。0〜1の間で表現され、1に近いほど信頼度が高いとみなされる。だいたい0.5あればそれなりに信頼できて、0.8を超えると結構信頼度が高い、みたいなものらしい。
Googleスプレッドシートを使った重回帰分析
XLMiner Analysis ToolPakを使う。以下よりインストール。
以下のようなデータを作成する
参考)https://data-viz-lab.com/multiple-regression-analysis

拡張機能から起動。Startが出てこなかったけどブラウザ開き直したら出た。
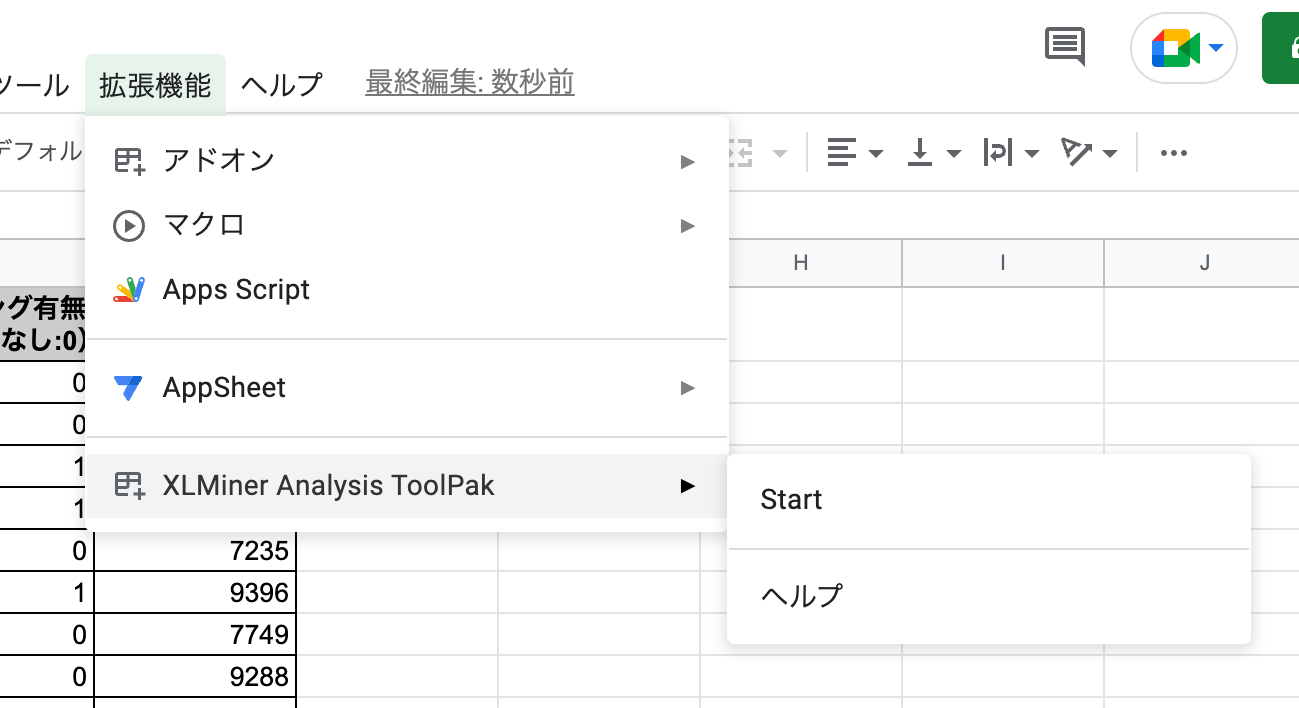
メニューから"Linear Regression"をクリック。必要な項目を入力していく。
- Y range: 目的変数の範囲を指定
- X range: 説明変数の範囲を指定
- Labels: 上記に項目名を含む場合はチェック
- Output Range: 結果を出力するセルを指定
OKをクリックすると解析結果が表示される。

回帰式は一番下のところから求められる
- Coefficients: 回帰係数
- Intercept: 切片
今回の場合だと回帰係数があまり意味をなしていないように思える。。。
ということで分析結果の評価を以下の点で行う。
- 回帰式の精度(補正R2=Adjusted R Square)
- 回帰式の有意性(回帰式が統計的に意味があるか?有意F=Significance F)
- 係数の有意性(係数が統計的に意味があるか?P-値=P-value)
- 説明変数の影響度(目的変数に与える影響度合い。t値=t value)
回帰式の精度(補正R2=Adjusted R Square)
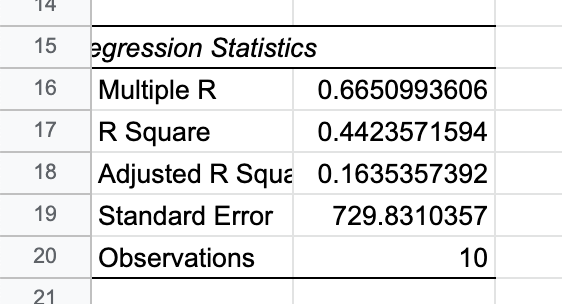
- 単回帰分析のR2と同じく、0〜1の間で1に近いほど精度が高い回帰式
- 今回は0.16で精度が低いと判断できる
回帰式の有意性(回帰式が統計的に意味があるか?有意F=Significance F)

- 有意Fが0.05未満であれば有用な回帰式。ただし自分で決めれる。0.05か0.01が多いらしい。
- 今回の結果だと0.28で有用ではないと判断できる。
係数の有意性(係数が統計的に意味があるか?P-値=P-value)

- 0.05未満ならその説明変数は目的変数に対して関係性があると判断。ただし自分で決めれる。0.05か0.01未満が多いらしい。
- 0.05以上なら分析に対象から外していく。
- 今回の場合はどれも0.05以上なので関係性がないと判断できる
説明変数の影響度(目的変数に与える影響度合い。t値=t value)

- t値の絶対値が大きければ影響が強いということになる。目安としては2以上。
- 今回の場合はどれも絶対値は2未満なので影響しないと判断できる
書きながら、参考にしたサイトと数字が違うなーと思っていたら、違うところ見てたみたいで、データが異なっていた。修正して再度やってみたらこうなる。

だいぶ近しいものになった。微妙に違うのはツールの違いなのかな。パラメータ変えたら変わるのかも。
XLMiner Analysis ToolPak の各項目については以下
Pythonで重回帰分析
ということで同じことをpandas/scikit-learnでもやってみる。
参考)https://qiita.com/karaage0703/items/f38d18afc1569fcc0418
pandasでデータフレーム作成
import pandas as pd
df = pd.DataFrame(
data={
"座席": [54, 75, 80, 85, 40, 76, 45, 70, 78, 74],
"徒歩時間": [6, 3, 1.5, 4, 7, 1.5, 9, 2, 7, 8],
"モーニング有無": [0, 1, 1, 1, 0, 1, 0, 1, 0, 1],
"限定商品数": [2, 4, 5, 1, 0, 6, 2, 6, 1, 4],
"売上": [7800, 8718, 9401, 8596, 7235, 9396, 7749, 9288, 7581, 8434],
}
)
df

説明変数と目的変数を取り出す。
x = df[["座席", "徒歩時間", "モーニング有無", "限定商品数"]]
x1 = df[["座席"]]
x2 = df[["徒歩時間"]]
x3 = df[["モーニング有無"]]
x4 = df[["限定商品数"]]
y = df[["売上"]]
説明変数が多いのでグラフ化はパス。
正規化は、説明変数ごとの単位・尺度の違いを吸収する。まずは一旦正規化無しで行う。
sscaler = preprocessing.StandardScaler()
sscaler.fit(x)
xss_sk = sscaler.transform(x)
sscaler.fit(y)
yss_sk = sscaler.transform(y)

import streamlit as st
from sklearn.linear_model import LinearRegression
model_lr = LinearRegression()
model_lr.fit(x, y)
st.text(f"回帰係数: {model_lr.coef_}")
st.text(f"切片: {model_lr.intercept_[0]}")
st.text(f"決定係数: {model_lr.score(x, y)}")
結果
回帰係数: [[ 4.26216474 -84.75096397 478.11874051 154.15560791]]
切片: 7781.777541863136
決定係数: 0.9678469000446034
スプレッドシートとほぼおなじになる。
次に正規化を行った上でやってみる。正規化手法は標準化を使用する(この辺難しくて理解できていない・・・)
model_lr_std = LinearRegression(fit_intercept=False)
model_lr_std.fit(xss_sk, yss_sk)
st.text(f"回帰係数: {model_lr_std.coef_}")
st.text(f"切片: {model_lr_std.intercept_[0]}")
st.text(f"決定係数: {model_lr_std.score(xss_sk, yss_sk)}")
結果
回帰係数: [[ 0.08339472 -0.3012271 0.30940085 0.42176262]]
切片: 9.344073462596507e-16
決定係数: 0.9678469000446034
得られた回帰係数を元に予測してみるが、正規化を行った場合は逆に元の単位にあわせて逆変換し直す必要がある
model_lr.predict(x)
model_lr_std.predict(xss_sk)
sscaler.inverse_transform(model_lr_std.predict(xss_sk))
結果
[[7811.73986971]
[8941.92817746]
[9244.52105502]
[8437.33203713]
[7359.00738359]
[9381.62800398]
[7519.12749516]
[9313.67953356]
[7675.12525154]
[8513.91119286]]
[[-0.80320544]
[ 0.68969526]
[ 1.08939956]
[ 0.02315861]
[-1.40123379]
[ 1.27050837]
[-1.18972618]
[ 1.18075313]
[-0.98366392]
[ 0.12431439]]
[[7811.73986971]
[8941.92817746]
[9244.52105502]
[8437.33203713]
[7359.00738359]
[9381.62800398]
[7519.12749516]
[9313.67953356]
[7675.12525154]
[8513.91119286]]
標準化なし=標準化+逆変換になれば、標準化なしの係数をそのまま使っていいということなのかな?
統計的解釈を行うには、statsmodelsを使う。標準化なしを使ってみる。
import statsmodels.api as sm
x_add_const = sm.add_constant(x)
model_sm = sm.OLS(y, x_add_const).fit()
st.text(model_sm.summary())
結果
OLS Regression Results
==============================================================================
Dep. Variable: 売上 R-squared: 0.968
Model: OLS Adj. R-squared: 0.942
Method: Least Squares F-statistic: 37.63
Date: 金, 10 2月 2023 Prob (F-statistic): 0.000634
Time: 19:42:34 Log-Likelihood: -63.297
No. Observations: 10 AIC: 136.6
Df Residuals: 5 BIC: 138.1
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 7781.7775 508.577 15.301 0.000 6474.439 9089.116
座席 4.2622 6.406 0.665 0.535 -12.204 20.728
徒歩時間 -84.7510 35.148 -2.411 0.061 -175.101 5.599
モーニング有無 478.1187 254.105 1.882 0.119 -175.079 1131.317
限定商品数 154.1556 47.716 3.231 0.023 31.497 276.815
==============================================================================
Omnibus: 0.382 Durbin-Watson: 2.200
Prob(Omnibus): 0.826 Jarque-Bera (JB): 0.471
Skew: 0.219 Prob(JB): 0.790
Kurtosis: 2.031 Cond. No. 593.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
標準化したものでもやってみる。
x_add_const_std = sm.add_constant(xss_sk)
model_sm_std = sm.OLS(yss_sk, x_add_const_std).fit()
st.text(model_sm_std.summary())
結果
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.968
Model: OLS Adj. R-squared: 0.942
Method: Least Squares F-statistic: 37.63
Date: 金, 10 2月 2023 Prob (F-statistic): 0.000634
Time: 19:44:18 Log-Likelihood: 2.9968
No. Observations: 10 AIC: 4.006
Df Residuals: 5 BIC: 5.519
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 9.437e-16 0.080 1.18e-14 1.000 -0.206 0.206
x1 0.0834 0.125 0.665 0.535 -0.239 0.406
x2 -0.3012 0.125 -2.411 0.061 -0.622 0.020
x3 0.3094 0.164 1.882 0.119 -0.113 0.732
x4 0.4218 0.131 3.231 0.023 0.086 0.757
==============================================================================
Omnibus: 0.382 Durbin-Watson: 2.200
Prob(Omnibus): 0.826 Jarque-Bera (JB): 0.471
Skew: 0.219 Prob(JB): 0.790
Kurtosis: 2.031 Cond. No. 4.36
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
係数や切片は当然違うけど、補正R2・有意F・P-値・t値は同じだから、この 解析そのものは有用であると判断しても良さそう。
あとはpredict()で予測すればよいということなのかなと思う。