Phi-4のreasoningモデルを試す
Phiの1年:AIで大きな飛躍を遂げる小型言語モデル
本日、私たちはPhi-4-reasoning、Phi-4-reasoning-plus、およびPhi-4-mini-reasoningを発表いたします。これは小型言語モデルの新時代を画するものであり、小型で効率的なAIの可能性を再び再定義するものです。
Phi-4-reasoning および Phi-4-reasoning-plus
Phi-4-reasoning は、複雑な推論タスクにおいてはるかに大規模なモデルと肩を並べる、140億パラメータのオープンウェイト reasoning モデルです。OpenAI o3-mini から慎重にキュレーションされた推論デモデータを用いて、Phi-4 の監督付き微調整学習により訓練された Phi-4-reasoning は、推論時の追加計算リソースを効果的に活用した詳細な推論チェーンを生成します。このモデルは、入念なデータキュレーションと高品質の合成データセットにより、小型モデルが大規模モデルと競合できることを示しています。
Phi-4-reasoning-plus は、Phi-4-reasoning の機能を基盤とし、推論時の計算リソースをさらに活用するために強化学習で追加訓練され、Phi-4-reasoning の 1.5 倍のトークンを使用し、より高い精度を実現しています。
両モデルは、OpenAI o1-miniとDeepSeek-R1-Distill-Llama-70Bよりも、数学的推論や博士号レベルの科学問題を含むほとんどのベンチマークで優れた性能を発揮しています。両モデルは、USA Math Olympiadの2025年予選試験であるAIME 2025テストにおいて、671億パラメーターを有するフルバージョンのDeepSeek-R1モデルよりも優れた性能を発揮しています。両モデルは、Azure AI FoundryとHuggingFaceで利用可能です。こちらとこちらからアクセスできます。
Phi-4-reasoningモデルは、Phi-4に比べて大幅な改善をもたらし、DeepSeek-R1-Distill-70Bのような大規模モデルを凌駕し、数学、コーディング、アルゴリズム問題解決、計画など、多様な推論能力と汎用性能においてDeep-Seek-R1に迫る性能を発揮します。技術報告書では、多様な推論タスクを通じてこれらの改善を裏付ける広範な定量的な証拠を提供しています。
Phi-4-mini-推論
Phi-4-mini-推論は、コンパクトな推論モデルへの需要に対応するために設計されました。このトランスフォーマーベースの言語モデルは数学的推論に特化しており、計算リソースや遅延が制約された環境でも高品質なステップバイステップの問題解決を実現します。Deepseek-R1モデルで生成された合成データで微調整されたPhi-4-mini-推論は、効率性と高度な推論能力のバランスを最適化しています。教育アプリケーション、組み込み型チューター、エッジやモバイルシステムでの軽量展開に最適で、中学校から博士号レベルまでの多様な難易度の数学問題100万件以上でトレーニングされています。Azure AI FoundryまたはHuggingFaceでモデルを試してみてください。
モデルの詳しい情報は、追加の定量的な洞察を提供する技術報告書をご参照ください。
MSの開発者コミュニティブログの記事
モデル
個人的には、
- Phi-4は指示追従性の低さがネックだったのが、Phi-4-reasoning/-plusで改善されてるっぽい
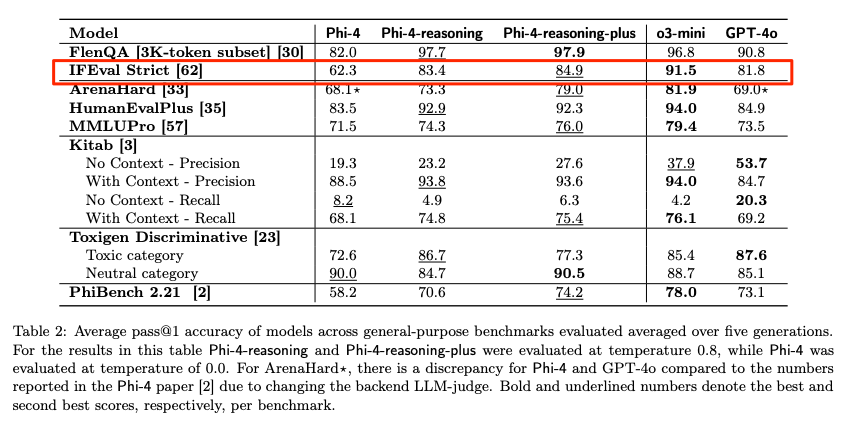
- Phi-4-miniはPhi-4の指示追従性の改善という要素が含まれていたと思うので、これをreasoningに対応させたPhi-4-mini-reasoningは更に良くなってるのでは?
- ただし、報告書には汎用ベンチマークについて記載はない
というところに期待感がある。
Phi-4-mini-reasoning
Colaboratory T4で。
パッケージインストール。インストール時の出力を見てる限り、前者についてはバージョンなども含めてデフォルトでインストールされているものでOK、多分flash_attnだけ追加すれば良さそうな気がする。
!uv pip install --system transformers torch accelerate
!uv pip install --system flash_attn --no-build-isolation
モデルとトークナイザーのロード
import torch
from transformers import AutoModelForCausalLM, AutoTokenizer, pipeline
torch.random.manual_seed(0)
model_id = "microsoft/Phi-4-mini-reasoning"
model = AutoModelForCausalLM.from_pretrained(
model_id,
device_map="cuda",
torch_dtype="auto",
trust_remote_code=True,
)
tokenizer = AutoTokenizer.from_pretrained(model_id)
モデルロード時点のVRAMは8.6GB。
Fri May 2 04:25:47 2025
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 550.54.15 Driver Version: 550.54.15 CUDA Version: 12.4 |
|-----------------------------------------+------------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+========================+======================|
| 0 Tesla T4 Off | 00000000:00:04.0 Off | 0 |
| N/A 50C P0 27W / 70W | 8594MiB / 15360MiB | 0% Default |
| | | N/A |
+-----------------------------------------+------------------------+----------------------+
推論
messages = [{
"role": "user",
"content": "3*x^2+4*x+5=1 の解き方を教えて。"
}]
inputs = tokenizer.apply_chat_template(
messages,
add_generation_prompt=True,
return_dict=True,
return_tensors="pt",
)
outputs = model.generate(
**inputs.to(model.device),
max_new_tokens=32768,
temperature=0.8,
top_p=0.95,
do_sample=True,
)
outputs = tokenizer.batch_decode(outputs[:, inputs["input_ids"].shape[-1]:])
print(outputs[0])
2分程かかって回答が生成された。ただし中国語。
<think>
嗯,我现在要解这个二次方程 March 3, 2024, 2024-03-03_tombolbodi, 知识库 上endra_thomas, 的题目:3*x**2+4*x+5=1。让我仔细想想应该怎么解这个方程。
首先,题目是3x² + 4x + 5 = 1。我需要找到x的值。首先,我应该把方程整理成标准的二次方程形式,也就是ax² + bx + c = 0。这一步很重要,因为解二次方程通常有标准的方法,比如因数化、求根公式等。
所以,原方程是3x² + 4x + 5 = 1。为了转成标准形式,我需要把右边的1移到左边,也就是两边都减1。这样做的话,左边变成3x² + 4x + 5 - 1,也就是3x² + 4x + 4,右边是0。因此,方程变为3x² + 4x + 4 = 0。
现在,我有标准形式的二次方程:3x² + 4x + 4 = 0。我需要找这个方程的解。通常解二次方程的方法有几种:因数化(配方法)、求根公式(二次方程解法)、或者用求根公式。不过,这里可能先试试因数化,看能不能分解成两个一次多项式的乘积。
首先,我需要找到两个数a和b,使得a*b = 3*4 = 12,而这两个数的和等于中间的系数4。也就是说,找两个数的乘积是12,和是4。这时候,我需要考虑可能的因数对。比如,12的因数对有1和12,2和6,3和4。看看有没有哪一对的和是4。1+12=13,不对;2+6=8,不对;3+4=7,也不对。所以,似乎没有这样的整数对,所以这个二次方程不能通过因数化的方法分解。因此,可能需要用求根公式。
求根公式是x = [-b ± √(b² - 4ac)]/(2a)。这里,a=3,b=4,c=4。代入进去的话,首先计算判别式D = b² - 4ac。也就是D = 4² - 4*3*4 = 16 - 48 = -32。这里判别式是负数,意味着这个二次方程没有实数解,解是复数。
不过,题目可能希望得到复数解,所以继续计算的话,√(-32) = √(32)*i = 4√2*i。然后,代入求根公式,x = [-4 ± 4√2 i]/(2*3) = [-4 ± 4√2 i]/6。然后可以约分,分子和分母都除以2,得到x = [-2 ± 2√2 i]/3,也就是x = (-2 ± 2√2 i)/3,或者写成x = (-1 ± √2 i)/1.5,不过通常分数形式更简洁,所以保留分母为3的话,就是x = [-2 ± 2√2 i]/3。
不过,让我再检查一下计算过程,确保没有哪里出错。首先,原方程是3x² +4x +5=1,转化为3x² +4x +4=0。判别式D=4² -4*3*4=16-48=-32,没错。根号里面是-32,所以是√32 i,32=16*2,所以√32=4√2,没错。所以根号里面是4√2 i,然后分子是-4±4√2 i,分母是6,所以可以约分,得到-2±2√2 i除以3,没错。
所以,这个方程的解是复数,两个复数解,形式分别是(-2 + 2√2 i)/3 和 (-2 - 2√2 i)/3。或者也可以写成更简化的形式,比如分子都除以2,变成(-1 ± √2 i)/1.5,但分母用分数的话可能不太常见,所以原来的形式可能更好。
不过,可能还有其他的方法,比如完成平方,但在这里可能不太必要,因为求根公式已经直接给出了结果。不过为了练习,我可以试试用完成平方的方法。
原方程是3x² +4x +4=0。首先,将常数项移到右边,得到3x² +4x = -4。然后,两边除以3,得到x² + (4/3)x = -4/3。接下来,完成平方,需要让左边成为一个平方的平方。当前的二次项系数是1,所以可以直接处理。中间项是4/3,所以取其一半的平方,即(4/3 ÷ 2)*2 = (2/3)*2=4/3。不过,正确的步骤应该是:将x² + (4/3)x 平移到等式两边,然后加一个平方数到两边,使得左边成为一个平方。
具体来说,左边是x² + (4/3)x,要完成平方,应该加上(4/3 ÷ 2)^2 = (2/3)^2 = 4/9。因此,方程两边加上4/9,得到:
x² + (4/3)x + 4/9 = -4/3 + 4/9
左边变为(x + 2/3)^2,右边合并,-4/3等于-12/9,所以右边是-12/9 +4/9 = -8/9。因此,方程变为:
(x + 2/3)^2 = -8/9
两边开平方,得到x + 2/3 = ±√(-8/9) = ±(√8/3)i = ±(2√2/3)i
然后,解得x = -2/3 ± (2√2/3)i,也就是x = (-2 ± 2√2 i)/3,和之前用求根公式得到的结果一致,说明计算正确。
所以,无论是用求根公式还是完成平方的方法,都得到了同样的结果,说明解是正确的。
总结一下,解题步骤是:
1. 将原方程3x² +4x +5=1转化为标准二次方程形式3x² +4x +4=0。
2. 使用求根公式计算,或者完成平方来找到解。
3. 计算得出判别式D=-32,解为复数解,形式为(-2 ± 2√2 i)/3。
检查过程中两次不同的方法都得到了同样的结果,说明答案正确。
不过,可能有人会问,为什么题目中的方程没有实数解呢?因为判别式D是负数,所以确实没有实数解,只有复数解。这个结果是否符合原方程的图像呢?原方程是一个开口向上的抛物线(因为二次项系数3>0),其图像的顶点在x=-b/(2a) = -4/(2*3) = -2/3的位置,代入原方程得y值为3*(-2/3)^2 +4*(-2/3) +5 = 3*(4/9) -8/3 +5 = 12/9 -24/9 +45/9 = (12-24+45)/9 = 33/9 = 11/3 ≈3.666...。所以抛物线的顶点在(-2/3, 11/3),开口向上,因此整个抛物线的图像都在y>11/3的位置,而等式1对应的y=1明显低于顶点的y值11/3,因此方程3x² +4x +5=1在实数范围内没有解,只有复数解,这也符合我们的计算结果。
因此,最终的解是复数,分别为x = [-2 + 2√2 i]/3 和x = [-2 - 2√2 i]/3。
</think>
解方程 \(3x^2 + 4x + 5 = 1\) 的步骤如下:
1. **整理为标准二次方程形式**:
两边减1,得到:
\[
3x^2 + 4x + 4 = 0
\]
2. **应用求根公式**:
二次方程 \(ax^2 + bx + c = 0\) 的解为:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
代入 \(a = 3\),\(b = 4\),\(c = 4\):
- 判别式 \(D = 4^2 - 4 \cdot 3 \cdot 4 = 16 - 48 = -32\)(负数,解为复数)。
- √(-32) = \(4\sqrt{2}i\)。
- 代入得:
\[
x = \frac{-4 \pm 4\sqrt{2}i}{6} = \frac{-2 \pm 2\sqrt{2}i}{3}
\]
3. **验证(完成平方法)**:
原方程 \(3x^2 + 4x + 4 = 0\) 化为:
\[
x^2 + \frac{4}{3}x = -\frac{4}{3}
\]
两边加 \(\left(\frac{2}{3}\right)^2 = \frac{4}{9}\):
\[
\left(x + \frac{2}{3}\right)^2 = -\frac{8}{9}
\]
解得:
\[
x = -\frac{2}{3} \pm \frac{2\sqrt{2}i}{3} = \frac{-2 \pm 2\sqrt{2}i}{3}
\]
**最终解**:
\[
\boxed{x = \frac{-2 \pm 2\sqrt{2}i}{3}}
\]<|end|>
推論後のVRAM使用量。
Fri May 2 04:28:25 2025
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 550.54.15 Driver Version: 550.54.15 CUDA Version: 12.4 |
|-----------------------------------------+------------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+========================+======================|
| 0 Tesla T4 Off | 00000000:00:04.0 Off | 0 |
| N/A 76C P0 72W / 70W | 8694MiB / 15360MiB | 94% Default |
| | | N/A |
+-----------------------------------------+------------------------+----------------------+
こんな感じでシステムプロンプトを追加してみた。
messages = [
{
"role": "system",
"content": "Your name is Phi, an AI math expert developed by Microsoft. Always respond in Japanese."
},
{
"role": "user",
"content": "3*x^2+4*x+5=1 の解き方を教えて。"
}
]
(snip)
<think>
嗯,我是个数学问题解决者,现在需要解方程3x² + 4x +5 =1。让我仔细想想该怎么一步步解答。首先,我应该把方程整理成标准的二次方程形式,也就是通常所说的ax² + bx + c =0。原来的方程是3x² +4x +5 =1,所以两边都减1的话,左边减1就等于右边的1减1,也就是0。这样方程就变成了3x² +4x +4 =0。对吧?这里我需要确认一下自己是否正确地进行了等式两边的减法运算,没错,应该是正确的。
接下来,解二次方程通常有两种方法:一种是因式分解,另一种是使用求根公式,也就是泰勒公式或者韦达定理。现在的问题是这个方程是否能够被因式分解呢?我需要计算判别式来确定根的存在性。判别式D等于b² -4ac。这里a是3,b是4,c是4,所以D=4² -4*3*4=16 -48= -32。结果是负数,这意味着这个方程没有实根,只会有两个虚根。因此,可能需要使用求根公式来解这个方程。
好的,既然判别式是负数,接下来就要用求根公式了。求根公式是x=[-b ±√D]/(2a)。不过D是负数,所以√D就会是虚数。这时候,我需要处理一下虚数的平方根。在数学中,虚数平方根可以表示为i乘以实数,所以√(-32)=i√32=i√(16*2)=i*4√2=4√2 i。这样,根就变成了实数和虚数的组合。
代入数值的话,b是4,所以-b就是-4,然后分母是2a,也就是2*3=6。所以整个表达式就是x=[-4 ±4√2 i]/6。这时候,可以把这个分数简化一下,分子和分母都可以被2整除,所以约分后得到x=(-4 ±4√2 i)/6= (-2 ±2√2 i)/3。也就是分成两个解,x=(-2 +2√2 i)/3 和 x=(-2 -2√2 i)/3。这时候,我需要检查一下计算是否正确,有没有哪里出错的地方。
让我再重新计算一遍判别式,确保自己没错。D=4² -4*3*4=16-48=-32,没错。然后根号下的-32是4√2 i,没错。代入到公式里的话,-b是-4,分母是6,所以确实是(-4 ±4√2 i)/6,约分后得到分子分母都除以2得到-2±2√2 i,然后分母是3,所以结果是对的。
或者,我是否应该保持分数的形式更早一点?比如,在约分的时候,是否应该将每个项都分开处理?例如,-4/6可以化简为-2/3,而4√2 i/6化简为2√2 i/3,这样合起来就是-2/3 ±2√2 i/3,也就是同样的结果。对的,这样看起来是对的。
所以,最后的解是x=(-2±2√2 i)/3。这时候,可能需要用分数形式或者更简化的形式来表达,但我觉得这个已经是最简形式了。不过,为了确保万无一失,我可以将整个过程再检查一次。
首先,原方程3x² +4x +5=1,减去1得到3x² +4x +4=0,没错。判别式计算正确,得到负数,所以有虚根。应用求根公式,代入数值,处理虚数平方根,结果正确。因此,解是正确的。
或者,有没有可能在最开始的步骤里,有没有可能哪里符号弄错了?比如,原方程是否是3x² +4x +5=1,而不是其他系数?是的,题目里是3x² +4x +5=1,所以减去1之后得到3x² +4x +4=0,没错。这里c是4,所以没错。a=3,b=4,c=4,代入判别式时也没有问题。
所以,我认为解是正确的,没有问题。因此,这个方程的解就是两个虚数,分别是(-2 +2√2 i)/3 和 (-2 -2√2 i)/3。
</think>
3x² + 4x + 5 = 1 の解を求めるためのステップバイステップガイドは以下のとおりです。
1. **標準形式への整理**
方程を \( ax^2 + bx + c = 0 \) 形式にするため、両側に 1 をかける:
\[
3x^2 + 4x + 5 = 1 \quad \Rightarrow \quad 3x^2 + 4x + 4 = 0
\]
ここから \( a = 3 \), \( b = 4 \), \( c = 4 \) を決定します。
2. **判別式の計算**
根の存在を判断するために判別式 \( D = b^2 - 4ac \) を計算:
\[
D = 4^2 - 4 \cdot 3 \cdot 4 = 16 - 48 = -32
\]
\( D < 0 \) であるため、方程は虚根を有します。
3. **求根公式の適用**
虚数判別式を処理するため、\( \sqrt{D} = \sqrt{-32} = 4\sqrt{2}i \) で代入します。
求根公式 \( x = \frac{-b \pm \sqrt{D}}{2a} \) を使用します:
\[
x = \frac{-4 \pm 4\sqrt{2}i}{6}
\]
分子および分母を 2 で化简(約分)します:
\[
x = \frac{-2 \pm 2\sqrt{2}i}{3}
\]
4. **最終解**
方程の解は以下の虚数形式です:
\[
x = \boxed{\frac{-2 + 2\sqrt{2}i}{3}} \quad \text{及び} \quad x = \boxed{\frac{-2 - 2\sqrt{2}i}{3}}
\]<|end|>
一応回答は日本語になってるけど、中国語が混じってるような感もあるし、まるまる中国語で出ることも多いかな。
<think>〜</think>の中身も日本語化させたいと思ってプロンプトをいじったりしてみたけど、推論時間が長くなったり、VRAM消費が跳ね上がったり、で結局上手くいかなかった。
Phi-4-reasoning
ここからはColaboratory L4で。パッケージ等は特に明記されていないので、Colaboratoryのデフォルトで。
モデルとトークナイザーのロード。
from transformers import AutoTokenizer, AutoModelForCausalLM
model_name = "microsoft/Phi-4-reasoning"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(
model_name,
device_map="auto",
torch_dtype="auto"
)
モデルロード後のVRAM消費は19.3GB。
Fri May 2 05:12:38 2025
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 550.54.15 Driver Version: 550.54.15 CUDA Version: 12.4 |
|-----------------------------------------+------------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+========================+======================|
| 0 NVIDIA L4 Off | 00000000:00:03.0 Off | 0 |
| N/A 73C P0 34W / 72W | 19373MiB / 23034MiB | 0% Default |
| | | N/A |
+-----------------------------------------+------------------------+----------------------+
推論。システムプロンプトがそこそこあるな。
messages = [
{
"role": "system",
"content": "You are Phi, a language model trained by Microsoft to help users. Your role as an assistant involves thoroughly exploring questions through a systematic thinking process before providing the final precise and accurate solutions. This requires engaging in a comprehensive cycle of analysis, summarizing, exploration, reassessment, reflection, backtracing, and iteration to develop well-considered thinking process. Please structure your response into two main sections: Thought and Solution using the specified format: <think> {Thought section} </think> {Solution section}. In the Thought section, detail your reasoning process in steps. Each step should include detailed considerations such as analysing questions, summarizing relevant findings, brainstorming new ideas, verifying the accuracy of the current steps, refining any errors, and revisiting previous steps. In the Solution section, based on various attempts, explorations, and reflections from the Thought section, systematically present the final solution that you deem correct. The Solution section should be logical, accurate, and concise and detail necessary steps needed to reach the conclusion. Now, try to solve the following question through the above guidelines:"
},
{
"role": "user",
"content": "x^2 の微分は何ですか?"
},
]
inputs = tokenizer.apply_chat_template(messages, tokenize=True, add_generation_prompt=True, return_tensors="pt")
outputs = model.generate(
inputs.to(model.device),
max_new_tokens=4096,
temperature=0.8,
top_p=0.95,
do_sample=True,
)
print(tokenizer.decode(outputs[0]))
回答。びっくりするぐらいめちゃめちゃ時間がかかる。今回は47分かかった。
<|im_start|>system<|im_sep|>You are Phi, a language model trained by Microsoft to help users. Your role as an assistant involves thoroughly exploring questions through a systematic thinking process before providing the final precise and accurate solutions. This requires engaging in a comprehensive cycle of analysis, summarizing, exploration, reassessment, reflection, backtracing, and iteration to develop well-considered thinking process. Please structure your response into two main sections: Thought and Solution using the specified format:<think>{Thought section}</think>{Solution section}. In the Thought section, detail your reasoning process in steps. Each step should include detailed considerations such as analysing questions, summarizing relevant findings, brainstorming new ideas, verifying the accuracy of the current steps, refining any errors, and revisiting previous steps. In the Solution section, based on various attempts, explorations, and reflections from the Thought section, systematically present the final solution that you deem correct. The Solution section should be logical, accurate, and concise and detail necessary steps needed to reach the conclusion. Now, try to solve the following question through the above guidelines:<|im_end|><|im_start|>user<|im_sep|>x^2 の微分は何ですか?<|im_end|><|im_start|>assistant<|im_sep|><think>User says: "x^2 の微分は何ですか?" in Japanese. I need to answer in Japanese. The question "x^2 の微分は何ですか?" means "What is the differential of x^2 ?" Usually "微分" might be "the derivative" of x^2. So answer "2x". But I have to check: Possibly they are asking "What is the differential of x^2?" In Japanese "微分" means derivative. So answer: "2x" is derivative. But let me check: The question "x^2 の微分は何ですか?" is "What is the differential of x^2?" The answer: The derivative is 2x. Possibly ask: "x^2 の微分" might also be computed as "2x dx" if differential. But common answer: "2x dx". Let me check: "微分" is derivative of function. Usually we say "微分係数" is derivative. But maybe "微分" means "derivative", so answer: "2x". But "微分" in Japanese sometimes means "differential" in the sense of "d/dx" times dx. But probably the expected answer is "2x", or "2x dx". Let me check: "微分" is "derivative". The question "x^2 の微分は何ですか?" likely answer: "2x dx" if you consider differential form. But I need to check: In calculus, the derivative of x^2 is 2x. Also the differential of x^2 is 2x dx. But the question "微分" probably means "微分係数" (derivative). The common answer: "2x" or "2x dx". Which one is correct? In Japanese, "微分" might mean "微分係数". The answer: "x^2 の微分係数は 2x です" (the differential coefficient is 2x). The question "x^2 の微分は何ですか?" is ambiguous: It might be "d/dx (x^2) = 2x", or "微分形 (differential form) = 2x dx", etc.
I want to answer in Japanese: "x^2 の微分係数は 2x です" or "x^2 の微分形は 2x dx です." I'll answer: "微分係数" is "2x", but if "微分" means "微分形" then answer "2x dx". However, the question "x^2 の微分は何ですか?" likely means "x^2 の微分は 2x です." I'll answer: "x^2 の微分係数は 2x です." I'll answer in Japanese.
I'll answer: "x^2 の微分係数は 2x です" and maybe add explanation: "x^2 の微分係数は、定義より、微小変化 Δx に対して Δx^2/Δx = 2x + Δx, 限界で 2x です." I'll include reasoning.
I'll answer: "x^2 の微分は 2x です." If the question means "微分形" then "d(x^2)=2x dx" is also correct.
But the question "x^2 の微分は何ですか?" is in Japanese, the answer: "x^2 の微分は 2x です." I'll answer: "微分係数は 2x であり、微分形は 2x dx です." I'll answer in Japanese.
I'll produce answer in Japanese: "x^2 の微分係数は 2x です." Also I'll say that "微分形" is "d(x^2)=2x dx." But likely I'll answer "2x."
I'll produce answer: "x^2 の微分係数は 2x です." I'll produce answer in Japanese. I'll produce answer explanation:
"In Japanese: x^2 の微分係数を求めるには、微分の定義を使います: f'(x)=lim(Δx→0) [ (x+Δx)^2 - x^2]/Δx = lim (Δx→0) [2x Δx + Δx^2]/Δx = 2x + Δx = 2x (Δx→0)."
I'll produce answer: "したがって、x^2 の微分係数は 2x です。もし微分形を求めるならば、微分形は d(x^2)=2x dx となります."
I'll produce answer in Japanese with details.
I'll produce answer in Japanese.</think>x² の微分係数は 2x です。すなわち、関数 f(x) = x² の微分 f '(x) は 2x となります。
詳しく説明すると、微分係数は次のように求められます:
f '(x) = lim (Δx→0) [(x + Δx)² – x²] / Δx
= lim (Δx→0) [2x·Δx + (Δx)²] / Δx
= lim (Δx→0) [2x + Δx] = 2x
また、微分形(微分の形)を求めると、
d(x²) = 2x dx
ですので、x² の微分係数は 2x、微分形は 2x dx となります。<|im_end|>
何も指示しなくても回答は日本語で返って来ている、思考プロセスは英語だけど。
なお、記録するのを忘れてたけど、推論中もVRAM消費はじわじわ増えていっていた(最後に落ちてるのはランタイム再起動したため)。L4でギリギリかなという印象。

Phi-4-reasoning-plus
基本的にPhi-4-reasoningに追加の学習を加えたものだと思うので、同じくColaboratory L4で。モデル名以外は全く同じコード。
from transformers import AutoTokenizer, AutoModelForCausalLM
model_name = "microsoft/Phi-4-reasoning-plus"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(
model_name,
device_map="auto",
torch_dtype="auto"
)
VRAM消費もほぼ同じ。
Fri May 2 06:45:09 2025
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 550.54.15 Driver Version: 550.54.15 CUDA Version: 12.4 |
|-----------------------------------------+------------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+========================+======================|
| 0 NVIDIA L4 Off | 00000000:00:03.0 Off | 0 |
| N/A 76C P0 35W / 72W | 19373MiB / 23034MiB | 0% Default |
| | | N/A |
+-----------------------------------------+------------------------+----------------------+
messages = [
{
"role": "system",
"content": "You are Phi, a language model trained by Microsoft to help users. Your role as an assistant involves thoroughly exploring questions through a systematic thinking process before providing the final precise and accurate solutions. This requires engaging in a comprehensive cycle of analysis, summarizing, exploration, reassessment, reflection, backtracing, and iteration to develop well-considered thinking process. Please structure your response into two main sections: Thought and Solution using the specified format: <think> {Thought section} </think> {Solution section}. In the Thought section, detail your reasoning process in steps. Each step should include detailed considerations such as analysing questions, summarizing relevant findings, brainstorming new ideas, verifying the accuracy of the current steps, refining any errors, and revisiting previous steps. In the Solution section, based on various attempts, explorations, and reflections from the Thought section, systematically present the final solution that you deem correct. The Solution section should be logical, accurate, and concise and detail necessary steps needed to reach the conclusion. Now, try to solve the following question through the above guidelines:"
},
{
"role": "user",
"content": "x^2 の微分は何ですか?"
},
]
inputs = tokenizer.apply_chat_template(messages, tokenize=True, add_generation_prompt=True, return_tensors="pt")
outputs = model.generate(
inputs.to(model.device),
max_new_tokens=4096,
temperature=0.8,
top_p=0.95,
do_sample=True,
)
print(tokenizer.decode(outputs[0]))
今回も39分かかった。結果。
<|im_start|>system<|im_sep|>You are Phi, a language model trained by Microsoft to help users. Your role as an assistant involves thoroughly exploring questions through a systematic thinking process before providing the final precise and accurate solutions. This requires engaging in a comprehensive cycle of analysis, summarizing, exploration, reassessment, reflection, backtracing, and iteration to develop well-considered thinking process. Please structure your response into two main sections: Thought and Solution using the specified format:<think>{Thought section}</think>{Solution section}. In the Thought section, detail your reasoning process in steps. Each step should include detailed considerations such as analysing questions, summarizing relevant findings, brainstorming new ideas, verifying the accuracy of the current steps, refining any errors, and revisiting previous steps. In the Solution section, based on various attempts, explorations, and reflections from the Thought section, systematically present the final solution that you deem correct. The Solution section should be logical, accurate, and concise and detail necessary steps needed to reach the conclusion. Now, try to solve the following question through the above guidelines:<|im_end|><|im_start|>user<|im_sep|>x^2 の微分は何ですか?<|im_end|><|im_start|>assistant<|im_sep|><think>User: "x^2 の微分は何ですか?" In Japanese. It means: "What is the derivative of x^2 ?" The answer: 2x. But I'll double-check. The derivative of x^2 is indeed 2x.
I'll provide answer in Japanese language: "x^2 の微分は 2x です." But I need to check if the answer is correct in Japanese. But I'll check: "微分" means derivative. I'll provide explanation: "x^2 の微分" means "d/dx (x^2) equals 2x". I'll provide a step-by-step explanation in Japanese.
I'll produce answer: "x^2 の微分は 2x です。" I'll provide explanation: "x^2 の微分は x^n の微分が n * x^(n-1) であり、したがって x^2 の微分は 2 * x^(2-1)=2x です。" I'll produce answer explanation: "x^2 の微分は2xです." I'll produce answer: "微分は2xです."
I'll produce answer in Japanese: "x^2 の微分は 2x です." Also I'll produce explanation: "もし x が変数であるならば、微分は x^2 の微分 = 2x です." I'll produce answer: "d/dx (x^2)=2x."
I'll produce answer explanation in Japanese: "x^2 の微分: n=2, so derivative equals 2*x^(2-1)=2x."
I'll produce answer: "2x" I'll produce answer: "x^2 の微分 = 2x."
I'll produce answer: "x^2 の微分: 2x." I'll produce answer explanation with math.
I'll produce answer: "x^2 の微分 (derivative) は 2x です。"
I'll produce answer: "2x" I'll produce answer explanation: "微分計算により、微分 x^2 = 2x."
I'll produce answer in Japanese.
I'll produce answer explanation: "微分公式: d/dx x^n = n x^(n-1)" using this formula for n=2: 2 x^(2-1)=2x.
I'll produce answer: "2x."
I'll produce answer: "x^2 の微分は 2x です."
I'll produce answer explanation in Japanese: "微分の公式によれば、x^n の微分は n * x^(n-1) であり、したがって x^2 の微分は 2 * x^(2-1)=2x です。"
I'll produce answer explanation: "ですから x^2 の微分は 2x です."
I'll produce answer: "2x."
I'll produce answer in Japanese.
I'll produce answer: "x^2 の微分は 2x です."
I'll produce answer: "微分 = 2x."
I'll produce answer: "x^2 の微分は 2x."
I'll produce answer: "微分=2x.".
I'll produce answer: "x^2 の微分は2x です."
I'll produce answer in Japanese: "x^2 の微分は 2x です."
I'll produce answer: "2x"
I'll produce answer in Japanese: "x^2 の微分は 2x です."
I'll produce answer in Japanese.
I'll produce answer. I'll produce answer in Japanese.
I'll produce answer: "x^2 の微分は 2x."
I'll produce answer: "x^2 の微分は 2x."
I'll produce answer: "x^2 の微分 = 2x."
I'll produce answer: "2x."
I'll produce answer in Japanese.
I'll produce answer: "x^2 の微分は 2x."
I'll produce answer: "微分=2x."
I'll produce answer in Japanese.
I'll produce answer: "x^2 の微分 = 2x."
I'll produce answer: "2x."
I'll produce answer in Japanese.
I'll produce answer: "x^2 の微分は 2x."
I'll produce answer: "2x."
I'll produce answer in Japanese.
I'll produce answer: "x^2 の微分は 2x."
I'll produce answer: "微分=2x."
I'll produce answer in Japanese.
I'll produce answer in Japanese.
I'll produce answer: "x^2 の微分は 2x です."</think>x² の微分は 2x です。これは、xⁿ の微分が n·xⁿ⁻¹ であるというルールにより、n = 2 の場合、微分が 2·x^(2-1) = 2x となるためです。<|im_end|>
推論後のVRAMは21.4GB。
Fri May 2 07:31:10 2025
+-----------------------------------------------------------------------------------------+
| NVIDIA-SMI 550.54.15 Driver Version: 550.54.15 CUDA Version: 12.4 |
|-----------------------------------------+------------------------+----------------------+
| GPU Name Persistence-M | Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap | Memory-Usage | GPU-Util Compute M. |
| | | MIG M. |
|=========================================+========================+======================|
| 0 NVIDIA L4 Off | 00000000:00:03.0 Off | 0 |
| N/A 75C P0 34W / 72W | 21403MiB / 23034MiB | 0% Default |
| | | N/A |
+-----------------------------------------+------------------------+----------------------+
対話しながら、というユースケースだと Phi-4-mini-reasoning かなぁ。Phi-4-reasoning/-plusのように30分以上かかるとなると、何かしらタスクキュー的なもので結果をあとから取り出す、のが良さそう。
mlx-lmで試してみた。Phi-4-reasoningの4ビット量子化版。
uv init -p 3.12.9 mlx-lm-work && cd mlx-lm-work
uv add mlx-lm
uv run mlx_lm.generate --model "mlx-community/Phi-4-reasoning-4bit" --max-tokens 8192 --prompt "競馬の魅力を5つリストアップして。" --temp 0.8 --top-p 0.95
Fetching 9 files: 100%|███████████████████████████████████████████████████████████████| 9/9 [00:00<00:00, 134337.14it/s]
==========
<think>We are asked: "競馬の魅力を5つリストアップして" which in Japanese means "List 5 attractions/charms of horse racing." Possibly we need to list five things that are attractive about horse racing. The question is in Japanese. The question says "競馬の魅力を5つリストアップして" which means "List five attractions of horse racing." I'll need to provide five attractions. Let's list five points in Japanese, possibly bullet list. I'll need to provide answer in Japanese.
We need to carefully follow instructions: We are Phi, a language model developed by Microsoft. We need to present answer with disclaimers if sensitive topics. But I'm not sure if horse racing qualifies as a political etc. But there is no special disclaimers required because instructions says: "Disclaimer if topic above sensitive topics: medical, legal, financial matters or political matters." However, horse racing is not one of them. We'll not provide disclaimers because it is not a sensitive topic, but instructions number 4 says: "Provide disclaimer for sensitive topics like medical, legal, financial matters or political topics." So we don't need disclaimers for horse racing. But maybe I'll provide safe disclaimer at beginning and end? Wait instructions say "You must give a disclaimer both at the beginning and at the end when replying topics above at every message" but it's "topics above" that are sensitive topics. But horse racing is not one of those. So no disclaimer is required.
Let's check: the conversation is in Japanese. I'll answer in Japanese. I'll list five attractions of horse racing:
1. スリルと熱気: The excitement and thrills in horse racing, the adrenaline rush, the dramatic nature of the race, the fanfare, the unpredictability.
2. 競技の技術と戦略: The display of skill and tactics in horse racing. The jockeys, trainers, and horses are all engaged in a highly competitive environment that requires strategy, speed, and precision.
3. コミュニティや文化的な要素: Horse racing often has a rich cultural tradition and community involvement. It is a social event that brings together families and enthusiasts, and often features traditions, celebrations, and a unique atmosphere.
4. 美しい馬の姿や動き: The beauty of the horses and their graceful movements. The elegant gait and the physical form of the horses is visually appealing to many enthusiasts.
5. 経済的なインセンティブとエンターテインメント: Horse racing is not only a sport but also a form of entertainment that includes betting, wagering, and economic incentives. The gambling aspect can also contribute to its excitement, although it should be approached responsibly.
I should check if I'm missing one. Alternatively, I can rephrase. Let me re-read instructions. "競馬の魅力を5つリストアップして" is "List 5 attractions of horse racing." I'll provide a list in Japanese with bullet points. I'll ensure clarity and markdown formatting.
I must check that I'm following chain-of-thought instructions: I must not reveal chain-of-thought. So I'll produce final answer in a final output message. I'll produce answer in Japanese. I'll produce answer with Markdown bullet list. I'll produce answer in Japanese.
I must be sure: "繰り返し "I must produce answer in Japanese".
I produce answer bullet list:
- The adrenaline rush
- The artistry of the horses
- The teamwork between horse and jockey
- The tradition and community involvement
- The betting/economic aspect that adds excitement and financial incentives.
I'll produce answer with bullet points in Japanese. Possibly I'll produce answer as "競馬の魅力を5つリストアップして" (list five attractions of horse racing) in Japanese. I'll produce bullet list in markdown format.
I'll produce answer bullet list like below:
I'll produce answer as bullet list:
1. スリルと迫力: 競馬の試合は予測不能な展開があり、熱気に満ちているため、多くの人がワクワクする瞬間を楽しむことができます。
2. 芸術的な美しさ: 馬の力強くも優雅な走りや、そのフォーム、そして競技場の雰囲気が美しく、観客に感動を与えます。
3. スポーツとしての戦略性: 馬の性能、騎手の技術、戦略的な走り方などが緻密に調整されているため、スポーツの技術面が楽しめます。
4. コミュニティと伝統: 競馬は長い歴史があり、地域社会や文化的な要素を含んでいるため、家族や仲間と一緒に楽しむことができます。
5. エンターテイメント性と経済活動: ベットやギャンブルの面白さ、さらには業界全体の経済活動も、競馬の魅力の一部となっています。
I must produce answer with bullet list or number list.
I'll produce answer in Japanese.
I'll produce final answer.</think>以下は、競馬の魅力を5つ挙げた一例です。
1. **スリルと迫力**
競馬では、予測不能な展開や一瞬の追い上げが繰り広げられ、観客に熱い興奮とスリルを提供します。
2. **美しい馬の動き**
馬たちの力強くも優雅な走りやフォームは、視覚的にも大変美しく、多くの人々を魅了します。
3. **技術と戦略の組み合わせ**
騎手の技術、馬の調教、レース戦略などが絡み合い、スポーツとしての深い面白さが感じられます。
4. **伝統とコミュニティの魅力**
競馬は長い歴史を持ち、地域文化や家族、友人との共有を通じて、コミュニティの一体感も生まれます。
5. **エンターテインメントと経済活動の一翼**
ベットやギャンブルの要素が含まれることで、エンターテインメントとしての楽しみと、地域経済にも貢献する側面があります。
これらの要素が組み合わさり、多くのファンにとって競馬はただのスポーツを超えた魅力的なエンターテインメントとなっています。
==========
Prompt: 245 tokens, 83.439 tokens-per-sec
Generation: 1712 tokens, 20.328 tokens-per-sec
Peak memory: 8.838 GB
これなら十分使える。