検索の評価指標をranxを使いながら理解する

kun432

ranxを使ってRAGのretrievalを評価するにあたって、

多数の評価指標があり、どれを使えばよいのか？
ranxの評価用データをどう作れば良いのか？

というところで理解が足りない気がしたので、

なるだけ図示化
ranxで実際にどのようなデータになるのか？

を試しつつ、それぞれの評価指標に対する理解を深めてみようと思う。ranxの使い方については1番上のリンクを参照。

図示化については以下の記事のイメージがとてもわかりやすかったので踏襲してみた。

その他参考にさせてもらった

kun432

Hits

検索された関連文書の「数」。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hits"],
    max_p=0.01
)

print(report)

#    Model        Hits
---  ---------  ------
a    run_test1       1

ふむ。では増やしてみる。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hits"],
    max_p=0.01
)

print(report)

2件になる。

#    Model        Hits
---  ---------  ------
a    run_test1       2

Qrelでは2件だけど、結果は1件だけの場合。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hits"],
    max_p=0.01
)

print(report)

1になる。

#    Model        Hits
---  ---------  ------
a    run_test1       1

逆にQrelでは1件だけだけど、結果は2件返ってきた場合。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hits"],
    max_p=0.01
)

print(report)

こちらも1になる。

#    Model        Hits
---  ---------  ------
a    run_test1       1

つまり基本的な考え方はこう。図示化の参考にさせていただいた記事にあわせてみた。

では少し違う例。クエリに対して関連文書が0件（1件返ってきたが関連していない）ような場合。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_2": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hits"],
    max_p=0.01
)

print(report)

当然0になる。

#    Model        Hits
---  ---------  ------
a    run_test1       0

次にQrel, Runが2回の場合で、1回は期待する関連文書が返ってきたけど、もう1回は正しくない場合。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
    },
    "q_2": {
        "d_2": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_2": 1,
    },
    "q_2": {
        "d_2": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hits"],
    max_p=0.01
)

print(report)

ここは平均化される。

#    Model        Hits
---  ---------  ------
a    run_test1     0.5

なるほど。クエリと関連ドキュメントが1対1のペアで、例えば100個のペアに対して検索した場合、ヒットは純粋に何件検索できたか？の割合を示すことになる。

ただし、1件のクエリに対して複数の関連ドキュメントが紐づいていると、1を超える数値を取りうるので、例えばクエリごとに関連ドキュメントの数が違ったりするとかになってくると、ややこしくなりそう。

kun432

Hit Rate

少なくとも1つの関連文書が検索されたクエリの割合。「少なくとも1つ」というのがキモ。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hit_rate"],
    max_p=0.01
)

print(report)

#    Model        Hit Rate
---  ---------  ----------
a    run_test1           1

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
    },
    "q_2": {
        "d_2": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
    },
    "q_2": {
        "d_1": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hit_rate"],
    max_p=0.01
)

print(report)

#    Model        Hit Rate
---  ---------  ----------
a    run_test1         0.5

1件の検索に複数の関連文書が紐づいている場合。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hit_rate"],
    max_p=0.01
)

print(report)

#    Model        Hit Rate
---  ---------  ----------
a    run_test1           1

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_3": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hit_rate"],
    max_p=0.01
)

print(report)

#    Model        Hit Rate
---  ---------  ----------
a    run_test1           1

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
    },
    "q_2": {
        "d_2": 1,
        "d_3": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
    },
    "q_2": {
        "d_2": 1,
        "d_4": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["hit_rate"],
    max_p=0.01
)

print(report)

#    Model        Hit Rate
---  ---------  ----------
a    run_test1           1

つまりこう。

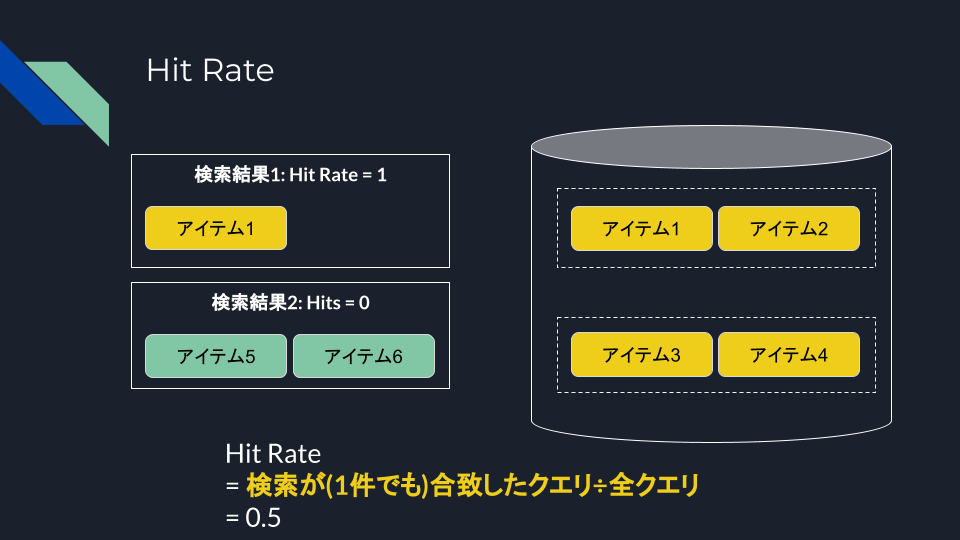
クエリに関連する文書の数は関係なく、少なくともクエリが「成功」した率、という感じ。逆に言うと1ではない場合は「検索できていない」クエリがあるということになるので、そちらのほうが重要なのかも。

kun432

HitsとHit Rateは、その検索システムが「いかに最低限の要求を満たしているか？」というのを測る指標なのかな、というのが個人的な印象。

複数の文書がある場合とか、ランキングの何位にいるか？みたいな、細かい「質」を測ることは難しいが、全体的な精度の雰囲気を測るには手軽な気がする。

kun432

Precision

Precisionは日本語だと「適合率」とか「精度」とか呼ばれることが多い。検索された文書のうち、関連性のある文書がどれだけあるか？の割合。

図については、以下の記事がわかりやすいので割愛。

ranxのドキュメントと上記の記事の数式は、書き方は違うけど、意味は同じだと思う。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_3": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_4": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["precision"],
    max_p=0.01
)

print(report)

#    Model          P
---  ---------  -----
a    run_test1  0.667

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
    "q_2": {
        "d_1": 1,
        "d_2": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
    "q_2": {
        "d_1": 1,
        "d_3": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["precision"],
    max_p=0.01
)

print(report)

#    Model         P
---  ---------  ----
a    run_test1  0.75

関連する文書が実際にはいくつあるか、ということは関係なくて、あくまでも検索結果の中に関連文書がどれだけ含まれるか？ということになるのだと思う。

kun432

Recall

Recallは日本語だと「再現率」というピンとこない表現になるけども、関連するすべての文書の総数のうち、検索でどれだけ抽出したかという比率。

図については、以下の記事がわかりやすいので割愛。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_3": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_4": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["recall"],
    max_p=0.01
)

print(report)

#    Model        Recall
---  ---------  --------
a    run_test1     0.667

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_3": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_3": 1,
        "d_4": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["recall"],
    max_p=0.01
)

print(report)

#    Model        Recall
---  ---------  --------
a    run_test1         1

ポイントとしては、Precisionの場合は、母数が検索結果なのに対して、こちらは検索で拾わなかったものも含めてすべての関連文書が母数になっているところかな。

いかに「網羅」できたか？という観点になる。

kun432

PrecisionとRecallについては以下がわかりやすい

情報検索システムの検索性能の評価を行う。情報検索システムの検索性能は主に正確性と網羅性の質的な観>>点から適合率(precision;精度ともいう)と再現率(recall)を、処理性能の量的な観点からスループットを測定することにより判定するのが一般的である。

※日本語Wikipediaより引用

上記が、日本語Wikipediaの「情報検索」に関する記事の中の、「検索性能の評価」というセクションの内容です。正直、何の事をいっているのかさっぱりわからないかと思いますが、 情報検索では「正確性」と「網羅性」 という指標を評価に用いている事がわかるかと思います。

適合率（precision）：正確性の指標

(snip)
これが、適合率は正確性の指標だという根拠で、 ユーザが検索を行って得た結果が、どれくらいユーザの意図したものに近いかどうか を判定する指標と言えます。

再現率（recall）：網羅率の指標

(snip)
つまり、再現率は検索エンジンに 元々インデックスされている （この場合は）「人工知能」の ドキュメントのうち、どの位のドキュメントがユーザに返却されたかを測定する指標なので、むしろ網羅率と表現する方が正解となります。

kun432

F1

F1はPrecisionとRecallの調和平均。一般的にPrecisionとRecallはトレードオフの関係にあるらしい。ChatGPTの例えがイメージしやすかった。

まず、「プレシジョン」と「リコール」というのは、何かを正しく見つけ出す能力を測るための指標です。例えば、図書館で好きな本を探す場合を考えてみましょう。

プレシジョン（精度） は、あなたが見つけた本の中で、本当に読みたかった正しい本はどれだけあるかを示します。つまり、あなたがたくさんの本を選んだとして、その中に本当に欲しい本がたくさん含まれていれば、プレシジョンは高いです。でも、たくさん選んだ本の中に、本当に読みたい本が少なければ、プレシジョンは低いです。

リコール（再現率） は、図書館にある本当に読みたい本全体から、あなたがどれだけ見つけ出せたかを示します。つまり、図書館にある自分が読みたい本が100冊あるとして、その中から90冊を見つけ出せればリコールは高いです。しかし、20冊しか見つけられなければリコールは低いです。

トレードオフとは、プレシジョンを高くしようとするとリコールが低くなりがちで、リコールを高くしようとするとプレシジョンが低くなりがちな関係のことです。これを図書館での本探しに例えると、本当に読みたい本だけを厳選して少なく選ぶと、選んだ本はほとんどが読みたい本でプレシジョンは高いですが、読みたい本全体の中から見つけ出せる本の数が少なくなるのでリコールは低くなります。逆に、読みたい本をなるべく多く見つけ出そうとしてたくさんの本を選ぶと、読みたくない本も多く含まれてしまうためプレシジョンは低くなりますが、読みたい本のほとんどをカバーできるのでリコールは高くなります。

要するに、プレシジョンとリコールはバランスをとる必要があり、どちらか一方を極端に追求すると、もう一方が犠牲になりがちです。理想的なのは、自分の目的に合わせて、この二つのバランスを上手く取ることです。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_3": 1,
        "d_4": 1,
        "d_5": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_6": 1,
        "d_7": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["precision", "recall", "f1"],
    max_p=0.01
)

print(report)

#    Model        P    Recall     F1
---  ---------  ---  --------  -----
a    run_test1  0.5       0.4  0.444

kun432

Precision、Recall、F1は、1つのクエリに対して関連文書が複数ある場合に意味が出てくると思う。

あと、ランキングの「質」を直接評価することにはならないと思う。実際にはtop-kで検索数は絞るので、その中に含まれるかどうか、という点ではランキングも影響はするのだけど、top-kに含まれていれば、1位だろうがk位だろうが影響しないと思う。

kun432

R-Precision

これちょっと難しかった。

\text{R-Precision} = \frac{\text{上位}R\text{件中の関連するドキュメントの数}}{\text{関連するドキュメントの総数}=R}

これってパッと見るとrecallと同じに思える。例えば

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_3": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["precision", "recall", "r-precision"],
    max_p=0.01
)

print(report)

#    Model        P    Recall    R-Prec
---  ---------  ---  --------  --------
a    run_test1    1     0.667     0.667

で、色々調べてみて、多分こういうことではないかと。

まずコード。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,
        "d_3": 1,
        "d_4": 1,
        "d_5": 1,
        "d_6": 0,
        "d_7": 0,
        "d_8": 0,
        "d_9": 0,
        "d_10": 0,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 0.8,
        "d_3": 0.6,
        "d_6": 0.4,
        "d_7": 0.3,
        "d_5": 0.2,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["precision", "recall", "r-precision"],
    max_p=0.01
)

print(report)

10件の文書があって、クエリに関連するものが5個含まれているとする。検索結果は6件返ってきて、その中に関連文書は4個含まれているとする。

この時の結果はこうなる。

#    Model          P    Recall    R-Prec
---  ---------  -----  --------  --------
a    run_test1  0.667       0.8       0.6

Precision

\text{Precision} = \frac{検索結果に含まれる関連するドキュメントの数}{検索結果の数} = \frac{4}{6} = 0.667

Recall

\text{Recall} = \frac{検索結果に含まれる関連するドキュメントの数}{関連するドキュメントの総数} = \frac{5}{6} = 0.8

R-Precision

\text{R-Precision} = \frac{\text{検索結果に含まれる関連するドキュメントの上位}R\text{件}}{\text{関連するドキュメントの総数(}R\text{)}} = \frac{3}{5} = 0.6

上位 $R$ 件ってのがミソっぽい。関連するドキュメントが6件ならば検索結果の上位6件中に何件含まれるか、ということ。図にするとこう。

precision/recallと同様に、クエリに対して複数の関連ドキュメントがある場合には意味が出てくるし、それに加えて、関連するドキュメントがより上位に集まっているかどうか、という観点になるイメージ。

参考

kun432

Bpref

Bpref （Binary Preference）は、関連性の判断が不完全な場合での評価指標。不完全というのは

全ての文書が評価されていない
全ての関連文書が判明していない

といったようなケース。

数式は以下。

\text{bpref}=\frac{1}{R}\sum_r{1 - \frac{|r\text{ よりも高くランクされた}n |}{R}}

$r$ : 関連する文書
$n$ : 関連しない文書
$R$ : 関連する文書の総数

ChatGPTによると以下。

各関連文書について、それよりも高くランクされた関連しない文書の割合を計算し、これを1から引いた値の平均を取ることで、Bprefを求めます。この方法により、関連文書がランキングの上位にどれだけ現れるか、つまり非関連文書にどれだけ先行してランクされるかを評価します。Bprefの最大値は1で、これは全ての関連文書が非関連文書よりも前に来る場合を意味します。逆に、関連文書が非関連文書に埋もれてしまう場合、Bprefの値は低くなります。

Bprefの特徴

不完全な評価データに対する頑健性: Bprefは、評価セットに含まれる全ての文書が評価されていなくても有効です。これは、関連性評価が難しい大規模なデータセットにおいて特に有用です。

非関連文書の扱い: Bprefは、関連文書がどれだけ非関連文書よりも優先的にランクされているかに焦点を当てています。これにより、非関連文書の大量存在が評価結果に与える影響を低減します。

等価性の仮定: Bprefはすべての関連文書が等しく重要であると仮定しますが、実際のアプリケーションでは関連度には様々な程度があり得ます。

まだピンとこないのでコードで。

from ranx import Qrels, Run, compare

# 一部分の関連・非関連文書はわかっていることが前提
qrels_dict = {
    "q_1": {
        "d_1": 1,  # 関連
        "d_2": 1,  # 関連
        "d_3": 1,  # 関連
        "d_4": 0,  # 非関連
        "d_5": 0,  # 非関連
        "d_6": 0,  # 非関連
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,     # 関連
        "d_4": 0.9,   # 非関連
        "d_2": 0.8,   # 関連
        "d_7": 0.7,   # 不明
        "d_3": 0.6,   # 関連
        "d_5": 0.5,   # 非関連
        "d_8": 0.4,   # 不明
        "d_6": 0.3,   # 非関連
        "d_9": 0.2,   # 不明
        "d_10": 0.1,  # 不明
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["bpref"],
    max_p=0.01
)

print(report)

#    Model        BPref
---  ---------  -------
a    run_test1    0.778

検索結果の少し順序を入れ替える。

関連・非関連の順序は同じ
不明なものは入れ替わる

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,  # 関連
        "d_2": 1,  # 関連
        "d_3": 1,  # 関連
        "d_4": 0,  # 非関連
        "d_5": 0,  # 非関連
        "d_6": 0,  # 非関連
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_7": 0.7,   # 不明
        "d_1": 1,     # 関連
        "d_8": 0.4,   # 不明
        "d_10": 0.1,  # 不明
        "d_4": 0.9,   # 非関連
        "d_2": 0.8,   # 関連
        "d_9": 0.2,   # 不明
        "d_3": 0.6,   # 関連
        "d_5": 0.5,   # 非関連
        "d_6": 0.3,   # 非関連
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["bpref"],
    max_p=0.01
)

print(report)

#    Model        BPref
---  ---------  -------
a    run_test1    0.778

同じ結果になっていることがわかる。

つまり、

Bpref （Binary Preference）は、関連性の判断が不完全な場合での評価指標。不完全というのは

全ての文書が評価されていない

全ての関連文書が判明していない

の状態だったとしても、関連性がわかっている一部については一定の順序が保たれている＝不明な文書はランキングの品質に対して中立である、ということ、だと理解した。

まとめるとこう

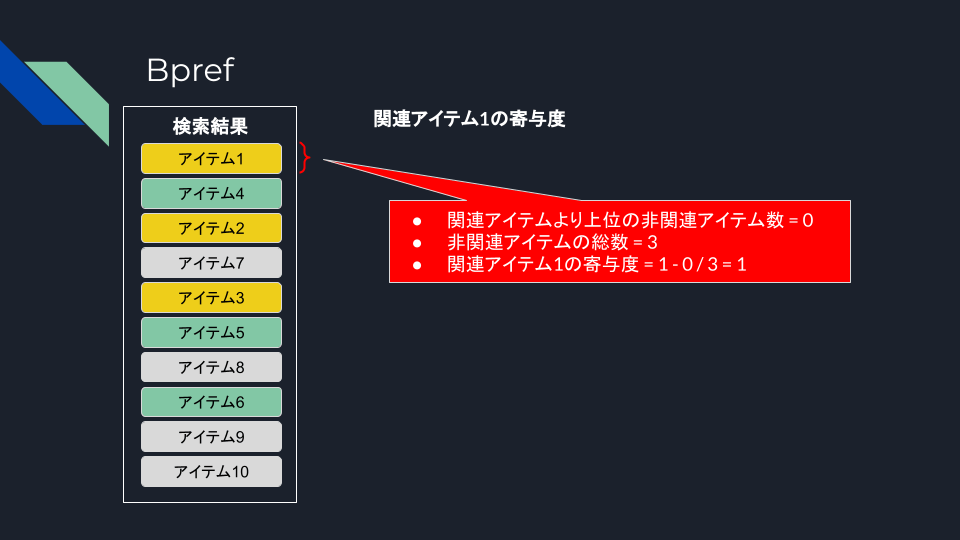
で、なんとなく思ったのは、

関連文書だけでなく、非関連文書の判別がある程度必要
全クエリに対して、まんべんなく関連・非関連の判別が必要

という感じかな。いずれにせよ、クエリに対して正解しかない、かつそれが1つだけ、みたいな、よくあるFAQデータセットだと厳しい気がした。

kun432

Rank-biased Precision

Rank-biased Precision (RBP) は、ランキングの先頭からユーザーが見る可能性が減少することを考慮した評価指標。ユーザは、ランキング上位の文書を見る可能性は高いが、下位に行くにつれてその可能性は減少するということを反映している。

\text{RBP} = (1 - p) \cdot \sum_{i=1}^{d}{r_i \cdot p^{i - 1}}

$p$ : ユーザが次のアイテムを見る確率（持続確率）。 $0 < p < 1$ の範囲で設定される。
$r_i$ : ランキングの位置 $i$ における文書の関連性スコア。文書が関連する場合は 1、そうでない場合は 0 または関連性の程度に応じた値を取る。
$d$ : 評価対象の文書の数、またはランキングリストの長さ。

文書がランキング上位であればあるほど評価に重みを付ける。 $p$ の値を変えることでユーザの行動をモデル化する。 $p$ が大きければユーザは多くの文書を見る、小さければ上位の文書しか見ない、ということになる。

$p$ によって同じデータでも評価が変わる。 $p$ が0.5の場合。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,  # 関連
        "d_2": 1,  # 関連
        "d_3": 1,  # 関連
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_4": 0.9,    
        "d_2": 0.8,   
        "d_5": 0.7,    
        "d_3": 0.6,    
        "d_6": 0.5,    
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["rbp.50"],
    max_p=0.01
)

print(report)

#    Model        RBP.50
---  ---------  --------
a    run_test1     0.656

$p$ を0.2と0.8で出してみるとこうなる。

#    Model        RBP.20    RBP.50    RBP.80
---  ---------  --------  --------  --------
a    run_test1     0.833     0.656      0.41

ただし、 $p$ の値には注意が必要に思う。例えば非常に高い値＝ユーザはランキング下位までを見ると想定した場合、

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,  # 関連
        "d_2": 1,  # 関連
        "d_3": 1,  # 関連
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 1,   
        "d_3": 1,    
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["rbp.99"],
    max_p=0.01
)

print(report)

#    Model        RBP.99
---  ---------  --------
a    run_test1      0.03

関連するドキュメントをきっちり返したとしてもRPBの値は低くなってしまう。実際にはそれほど高い値を設定するのはあまり意味がないと思うけど。

まとめるとこうかな。いい感じで図示化できなくて、もはやあまり意味がないかもだけど。

この指標は、明確に複数の文書が紐づいている場合にランキングの順序に意味が出てくる感じ。

kun432

(Mean) Reciprocal Rank

Reciprocal Rankは、最初に検索された関連文書の順位の逆数をスコアとする。つまり、1位は1、2位は1/2、3位は1/3という感じ。これを全クエリで平均したものを、MRR(Mean Reciprocal Rank)と呼ぶ。

Reciprocal Rank = \frac{1}{rank}

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_3": 1,
    },
    "q_2": {
        "d_4": 1,
        "d_6": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_3": 1,
        "d_1": 0.9,   
        "d_2": 0.8,    
    },
    "q_2": {
        "d_6": 1,
        "d_4": 0.9,   
        "d_5": 0.8,    
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["mrr"],
    max_p=0.01
)

print(report)

#    Model        MRR
---  ---------  -----
a    run_test1      1

上記の例だと、

q1で最初に出てきた関連があるドキュメントはd_3で1位、つまりReciprocal Rankは1
q2で最初に出てきた関連があるドキュメントはd_6で1位、つまりReciprocal Rankは1
上記の平均、すなわちMRRは1となる

MRRは0〜1の間の数字で1に近いほうが正確ということで、上記の例では良い結果となる。

少し検索結果を入れ替えてみる。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_3": 1,
    },
    "q_2": {
        "d_4": 1,
        "d_6": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_2": 1,   # 非関連
        "d_3": 0.9, # 関連
        "d_1": 0.8, # 関連
    },
    "q_2": {
        "d_5": 1,   # 非関連
        "d_7": 0.9, # 非関連    
        "d_6": 0.8, # 関連      
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["mrr"],
    max_p=0.01
)

print(report)

#    Model        MRR
---  ---------  -----
a    run_test1  0.417

q1で最初に出てきた関連があるドキュメントはd_3で2位、つまりReciprocal Rankは1/2=0.5
q2で最初に出てきた関連があるドキュメントはd_6で3位、つまりReciprocal Rankは1/3=0.333
上記の平均、すなわちMRRは0.4165≒0.417となる

図にするとこう。

非常にシンプルにランキングの重みを評価できるのだけども、以下のデメリットがある。

1つの正解にしか焦点が当たっていない

MRRは最初に見つかった関連文書の順位のみを考慮するため、検索結果の上位に複数の関連文書が存在したとしても、それらのランキングはスコアに反映されない。つまり、検索結果全体の質を完全に評価するのには適していない場合がある。

平均化により個々のクエリ評価が見えなくなる

MRRに限った話ではないが、MRRは複数のクエリに対するReciprocal Rankの平均となるため、個々のクエリごとの性能差異が失われる可能性がある。あるクエリでは良い性能だが、他のクエリで低い性能というようなケースがある場合、全体としての性能が不正確に評価されうる。

検索結果が多い場合に過小評価される

関連文書が検索結果のリストの下位にある場合、MRRのスコアは大きく低下するため、実際よりも低く評価される場合がある。ユーザが検索結果をじっくり掘り下げていく傾向がある場合、MRRでは正しい評価にならない場合がある。

関連文書が単一であることを想定している

MRRは各クエリに対して一つの「正解」となる関連文書が前提となるが、複数の関連文書がある場合には正しい評価ができない可能性がある。

kun432

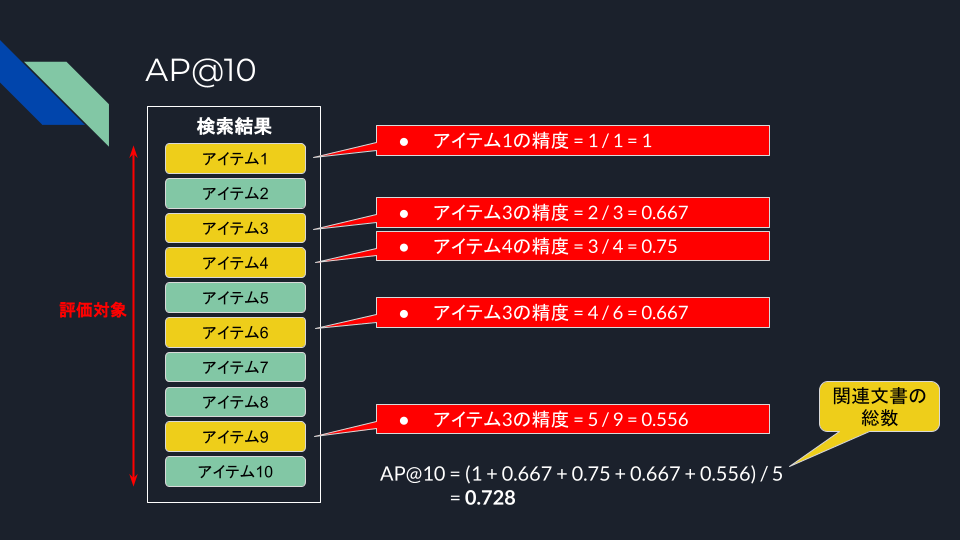
(Mean) Average Precision （MAP）

AP（Average Precision, AP）は特定のクエリに対して、ランキング内の各位置での精度の平均。これを複数のクエリにわたって平均を取ったのがMAP。カットオフ（@）が重要になってくる。

APは以下の記事で図示されていてわかりやすい。

まずはシンプルに、1クエリだけのMAP、つまり実質的にはAPを算出してみる。カットオフは3, 5, 10で。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_3": 1,
        "d_4": 1,
        "d_6": 1,
        "d_9": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 0.95,
        "d_3": 0.9,
        "d_4": 0.85,
        "d_5": 0.8,
        "d_6": 0.75,
        "d_7": 0.7,
        "d_8": 0.65,
        "d_9": 0.6,
        "d_10": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["map@3", "map@5", "map@10"],
    max_p=0.01
)

print(report)

#    Model        MAP@3    MAP@5    MAP@10
---  ---------  -------  -------  --------
a    run_test1    0.333    0.483     0.728

んー、Precision的には@3をtop-k=3と考えればカバーできてるじゃん、という気がするのだけども、APだと逆に小さな値になってしまう。いまいち腑に落ちない感があったので、計算過程もまとめてみた。

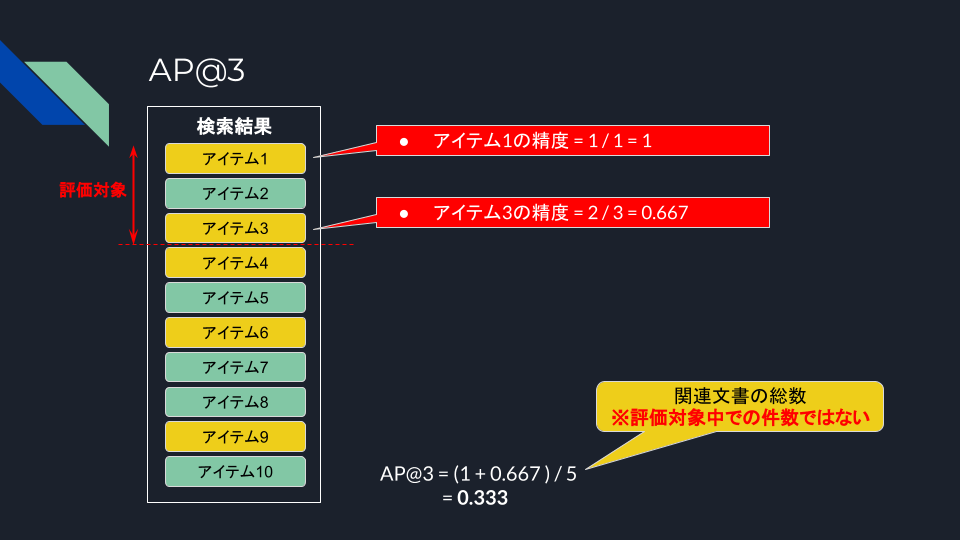
平均化する意味はなんとなくわかるんだけど、全関連文書で割るのがRecall的なんだよなぁ・・・

ということで教えてChatGPT先生！

User:
ちょっと疑問に思ったのは、そもそも、なんで全関連文書で割るんでしょうか？Average Precisionという感覚からするとカットオフ範囲内の関連文書数で割ればいいと思うのですが。

ChatGPT:
Average Precision (AP) を計算する際に全関連文書で割る理由は、検索システムの性能を評価する際に、そのシステムが関連文書をどの程度効率的に見つけられるかを全体的に評価する必要があるからです。ここでの「全体的」とは、検索結果全体にわたって、という意味です。

APの計算では、検索結果リストの各点で関連文書が見つかるたびに精度を計算し、それらの精度の平均を取ります。このとき、 全関連文書数 で割ることによって、検索結果の全範囲にわたるシステムの性能を反映させます。つまり、検索システムが全関連文書をどれだけ前の方に持ってくることができるか、ということを評価するわけです。

カットオフ範囲内の関連文書数で割るという方法も考えられますが、この方法では、検索結果の先頭に関連文書が集中している場合には高いスコアを得られますが、重要な関連文書が検索結果の後半にしか現れない場合の評価を適切に反映できません。つまり、全関連文書数で割ることによって、検索結果の全体を通じたシステムの性能をより公平に評価することができるのです。

APを計算する際に全関連文書数で割ることは、検索システムが全ての関連文書をどれだけ上位にランク付けできるか、ということを重視するためです。検索システムの目的は、ユーザーが求めている情報をできるだけ早く、かつ正確に提供することにあります。そのため、全関連文書をどれだけ効果的に見つけ出し、上位にランク付けできるかが重要な指標となるわけです。

User:
何となく仰ってることは理解するんですが、その場合カットオフを関連文書数以下の値に設定する意味合いが無い気がします。

ChatGPT:
カットオフを関連文書数以下の値に設定する意味についてのご質問は、非常に良い指摘です。実際、カットオフを関連文書数以下に設定することには、いくつかの意味合いがありますが、その効果や目的は、評価の文脈や検索タスクの特性によって異なります。

カットオフ設定の意味合い

ユーザー行動の模倣:
多くの場合、ユーザーは検索結果の最初の数件しか見ない傾向があります。特に、Web検索の文脈では、ユーザーが最初の1ページ目、つまり上位10件程度しか確認しないことが多いです。カットオフを関連文書数以下、例えば上位5件や10件に設定することは、このようなユーザー行動を模倣し、システムが最も重要な情報をどれだけ早く提供できるかを評価するために有効です。

初期精度の重視
情報検索システムや推薦システムでは、上位に表示されるアイテムの品質が非常に重要です。ユーザーの満足度やエンゲージメントは、最初に提示される情報に大きく依存するため、初期精度（上位数件の精度）に重きを置く評価が求められます。カットオフを短く設定することで、システムが上位にどれだけ関連性の高い文書を配置できているかを重点的に評価できます。

性能の微細な差異の検出:
カットオフを関連文書数以下に設定すると、検索システム間の性能の微細な差異を検出しやすくなります。特に競争が激しい検索エンジンや推薦システムの開発では、初期の数件におけるわずかな改善も大きな価値を持ちます。このような設定により、微細な改善点を識別し、システムの最適化に役立てることができます。

総合的な評価とバランス

ただし、カットオフを関連文書数以下に設定することが常に適切というわけではありません。評価の目的や検索タスクの特性に応じて、適切なカットオフを選択する必要があります。全体的な性能評価や、より深い検索結果におけるシステムの振る舞いを理解するためには、より長いカットオフを設定することも重要です。

結局のところ、カットオフの設定は、評価したいシステムの特性や、ユーザーの検索行動をどの程度反映させたいかによって決定されるべきです。そして、複数のカットオフで評価を行い、異なる視点からシステムの性能を検証することが、より包括的な理解に繋がります。

うーん、難しい。。。ただ、「上位に来るものが重要、上位しか見ないだろう」という前提が自分の中にはあったのは間違いない。そもそもRAGでは全部のランキング結果をコンテキスト内に収めれるわけではないし。検索を、上から下まで「全体的に」「公平に」評価するという観点を踏まえたのがMAPということなのだろうと思う。

もう少し深堀りで聞いてみた。

User:
クエリに対して関連文書が常に1つしかないようなケースだと、カットオフの意味合いは変わりますよね？

ChatGPT:
はい、クエリに対して関連文書が常に1つしかないようなケースでは、カットオフの意味合いは確かに変わります。このようなケースでは、情報検索システムの評価におけるカットオフの設定は、主に以下のような観点で異なる意味を持ちます。

カットオフの意味合いとその変化

最初の関連文書の発見に焦点:
関連文書が1つしかない場合、評価はシステムがその唯一の関連文書をどれだけ早くユーザーに提示できるかに焦点を当てます。この場合、カットオフはその関連文書が上位にあるかどうかを評価するための指標となります。初期精度（例えば、上位1件または上位3件での精度）が特に重要視されます。

ユーザー体験のシミュレーション:
このようなケースでは、ユーザーが目的の情報を見つけるまでの体験をシミュレートすることができます。ユーザーは通常、必要な情報を見つけ次第、検索を終了します。したがって、カットオフはユーザーがどの程度効率的にその情報を見つけられるかを示す指標になります。

システムの精度と効率のトレードオフ:
関連文書が1つしかない場合、システムは可能な限りその文書を上位にランク付けしようとします。ここでのカットオフは、システムがどれだけ効率的に関連情報を提供できるか、すなわち精度と効率のバランスをどのように取っているかを評価するための手段です。

評価指標の選択に影響:
このシナリオでは、Mean Reciprocal Rank (MRR) や Precision at K (P@K) など、特定の関連文書をいかに早く見つけられるかを測る指標が特に有効です。カットオフはこれらの指標を用いてシステムの性能を評価する際の基準点となります。

結論

クエリごとに関連文書が1つしかない場合、カットオフはシステムがその関連文書をどれだけ迅速に、かつ正確にユーザーに提供できるかを評価するための重要な要素になります。このシナリオでは、カットオフを超える検索結果の数は関連文書を見つける能力と直接的な関連は薄く、初期の数件におけるシステムの性能が特に重視されます。そのため、評価指標やカットオフの設定は、この特定の情報発見プロセスを反映するように選ばれるべきです。

ふむ、おっしゃるとおり、それならばMAPではなくて、MRRとかPrecisionで良さそう。クエリに対して複数の関連文書が紐づいている場合にMAPは有効になると理解した。あと網羅できているかの観点もあるように思えるので、シンプルなPrecisionだけでは測れないようなケースに良いのだと思った。

kun432

ここまでやみくもに調べつつで進めてきたけど、改めて以下の記事を見ると、良くまとまっていると感じた。

後でもう一度じっくり読む。

kun432

DCG/NDCG

DCG

NDCG

まず、DCG（Discounted Cumulative Gain）は、検索結果のランキング中のアイテムの関連度が下位になるほど関連性スコアを割り引く、つまり、上位にあるほど高いスコアを与えることで、ランキング全体の評価を行う。

DCG = \displaystyle\sum_{i=1}^n\frac{rel_i}{log_2(i + 1)}

$i$ : ランキングの位置
$rel_i$ : ランキング位置 $i$ における関連性スコア
$log_2(i+1)$ : 割引因子。ランキングが下がるにつれて関連性スコアの寄与を小さくする

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_4": 1,
        "d_8": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 0.95,
        "d_3": 0.9,
        "d_4": 0.85,
        "d_5": 0.8,
        "d_6": 0.75,
        "d_7": 0.7,
        "d_8": 0.65,
        "d_9": 0.6,
        "d_10": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["dcg"],
    max_p=0.01
)

print(report)

#    Model        DCG
---  ---------  -----
a    run_test1  1.746

計算過程をまとめるとこう

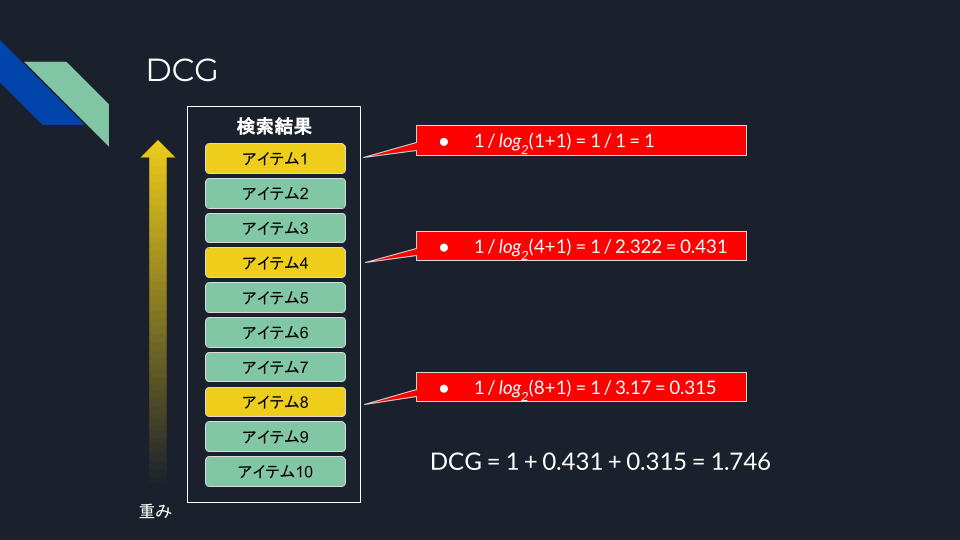
見てわかるように、DCGが取りうる値の範囲は、最低は0だが、最大は関連性データや結果によって異なり、理論上は無限大になる。ただ実際には関連性データや結果から上限は制限される。まあ少なくとも0〜1の範囲で決まるものではないということ。

カットオフを設定してみるとこうなる。

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["dcg@3", "dcg@5", "dcg@10"],
    max_p=0.01
)

#    Model        DCG@3    DCG@5    DCG@10
---  ---------  -------  -------  --------
a    run_test1        1    1.431     1.746

で、次にNDCG（Normalized Discounted Cumulative Gain）は、名前にもある通り、DCGを正規化したもの。DCGでは、関連性スコアの設定や検索結果の数によって、スコアの尺度が異なってくるため、比較が難しい。これを正規化することで0〜1の範囲に収めて比較しやすくしたのがNDCG。

数式はこう

NDCG = \frac{DCG}{IDCG}

$IDCG$ は「理想的（Ideal）」なDCG、つまり、検索結果が関連性の高い順に並んでいる場合のDCGの最大値を指す。つまりこの状態。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_4": 1,
        "d_8": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_4": 1,
        "d_8": 1,
        "d_2": 0.95,
        "d_3": 0.9,
        "d_5": 0.8,
        "d_6": 0.75,
        "d_7": 0.7,
        "d_9": 0.6,
        "d_10": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["dcg"],
    max_p=0.01
)

print(report)

#    Model        DCG
---  ---------  -----
a    run_test1  2.131

関連性スコアの高いものが検索結果上位1〜3位を占めている理想的な状態であり、この時のDCGを分母として正規化するということになる。

from ranx import Qrels, Run, compare

qrels_dict = {
    "q_1": {
        "d_1": 1,
        "d_4": 1,
        "d_8": 1,
    },
}

qrels = Qrels(qrels_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 0.95,
        "d_3": 0.9,
        "d_4": 0.85,
        "d_5": 0.8,
        "d_6": 0.75,
        "d_7": 0.7,
        "d_8": 0.65,
        "d_9": 0.6,
        "d_10": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test1")

report = compare(
    qrels=qrels,
    runs=[run1],
    metrics=["ndcg"],
    max_p=0.01
)

print(report)

#    Model        NDCG
---  ---------  ------
a    run_test1   0.819

答え合わせしてみる。

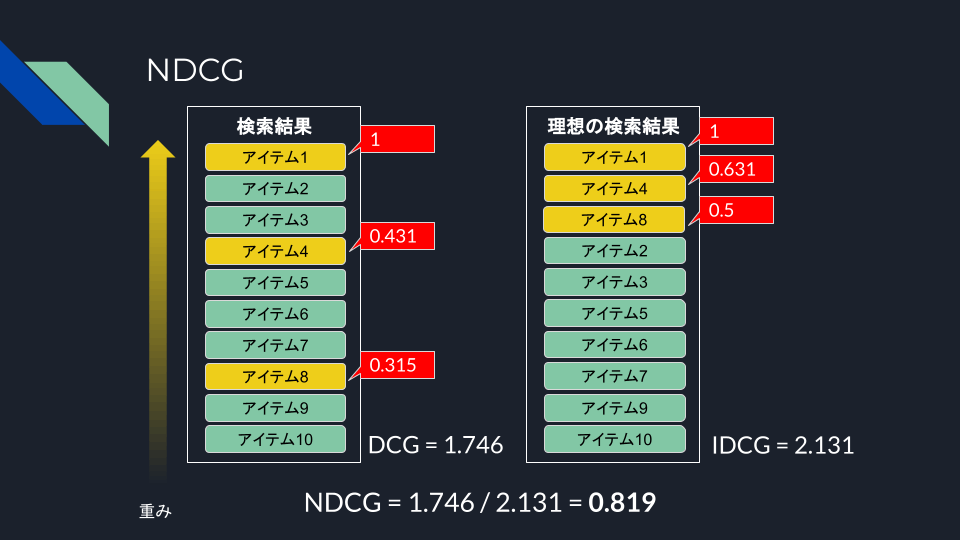
NDCG = \frac{DCG}{IDCG} = \frac{1.746}{2.131} = 0.819

kun432

DCG Burges/NDCG Burges

DCG Burges

NDCG Burges

DCG Burges/NDCG Burgesは、DCG2/NDCG2とも呼ばれる、DCG/NDCGのバリエーションで、考え方の基本は同じだけどもDCGの数式が異なる。

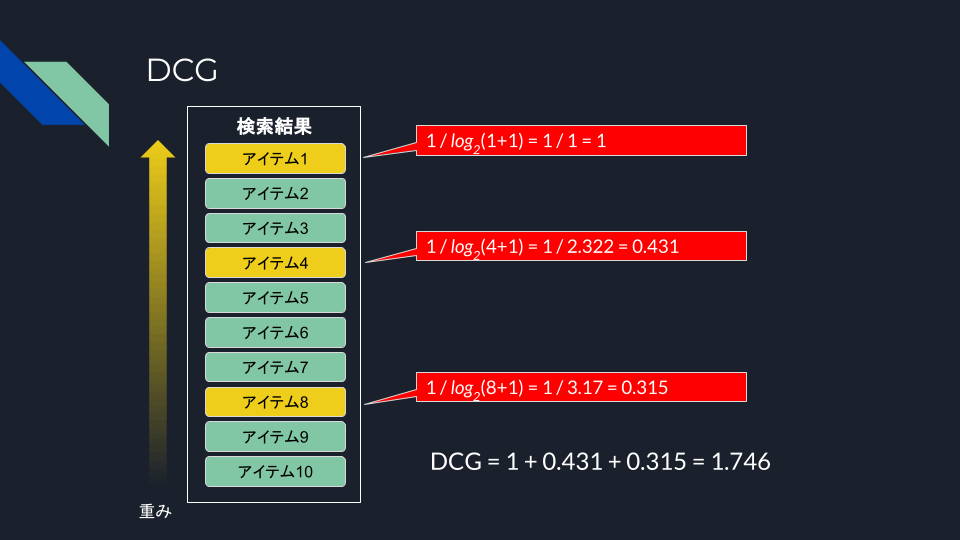
まず、上で行ったDCGの計算式は以下。

DCG = \displaystyle\sum_{i=1}^n\frac{rel_i}{log_2(i + 1)}

これに対して、DCG Burgesでは以下となる。

DCG = \displaystyle\sum_{i=1}^n\frac{2^{rel_i}-1}{log_2(i + 1)}

で、関連度スコアが0 or 1の場合には、上記のどちらの場合でも等価となる。

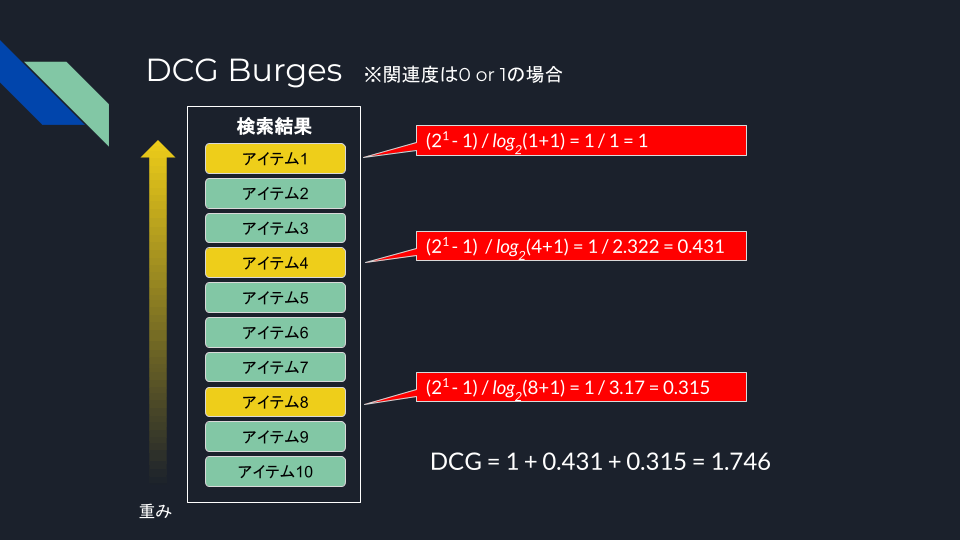
DCG/NDCGでは説明しなかったが、DCG/NDCGでは関連度スコアを0 or 1のバイナリだけでなく、複数の値からなるグレードで指定することもできる。

例えば以下のような感じ。

qrels_dict = {
    "q_1": {
        "d_1": 3,   # 関連度がかなり高い
        "d_4": 2,   # 関連度が結構高い
        "d_8": 1,   # 関連度が高い
    },
}

関連度スコアがバイナリか？それともグレードか？で結果の数値が変わってくる。

from ranx import Qrels, Run, compare

qrels1_dict = {
    "q_1": {
        "d_1": 1,
        "d_4": 1,
        "d_8": 1,
    },
}

qrels1 = Qrels(qrels1_dict, name="qrel_test1")

qrels2_dict = {
    "q_1": {
        "d_1": 3,
        "d_4": 2,
        "d_8": 1,
    },
}

qrels2 = Qrels(qrels2_dict, name="qrel_test2")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 0.95,
        "d_3": 0.9,
        "d_4": 0.85,
        "d_5": 0.8,
        "d_6": 0.75,
        "d_7": 0.7,
        "d_8": 0.65,
        "d_9": 0.6,
        "d_10": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test")

print("=== binary relavancy ===")
report = compare(
    qrels=qrels1,
    runs=[run1],
    metrics=["dcg", "ndcg", "dcg_burges", "ndcg_burges"],
    max_p=0.01
)
print(report)

print()

print("=== graded relavancy ===")
report = compare(
    qrels=qrels2,
    runs=[run1],
    metrics=["dcg", "ndcg", "dcg_burges", "ndcg_burges"],
    max_p=0.01
)
print(report)

=== binary relavancy ===
#    Model       DCG    NDCG    DCG Burges    NDCG Burges
---  --------  -----  ------  ------------  -------------
a    run_test  1.746   0.819         1.746          0.819

=== graded relavancy ===
#    Model       DCG    NDCG    DCG Burges    NDCG Burges
---  --------  -----  ------  ------------  -------------
a    run_test  4.177   0.877         8.607          0.916

関連度スコアがバイナリの場合にはどちらも変わらないが、グレード化されたスコアの場合に違いが出ているのがわかる。図にまとめると以下。

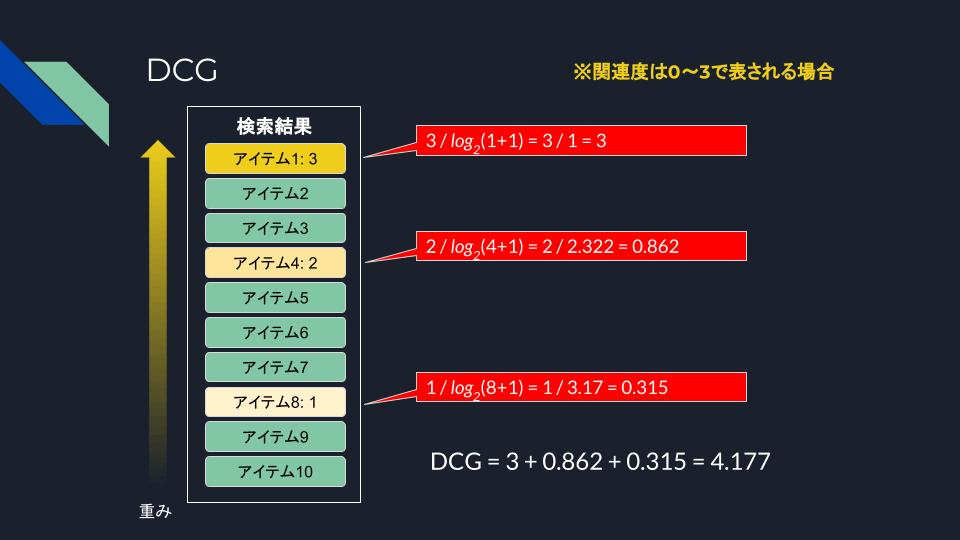
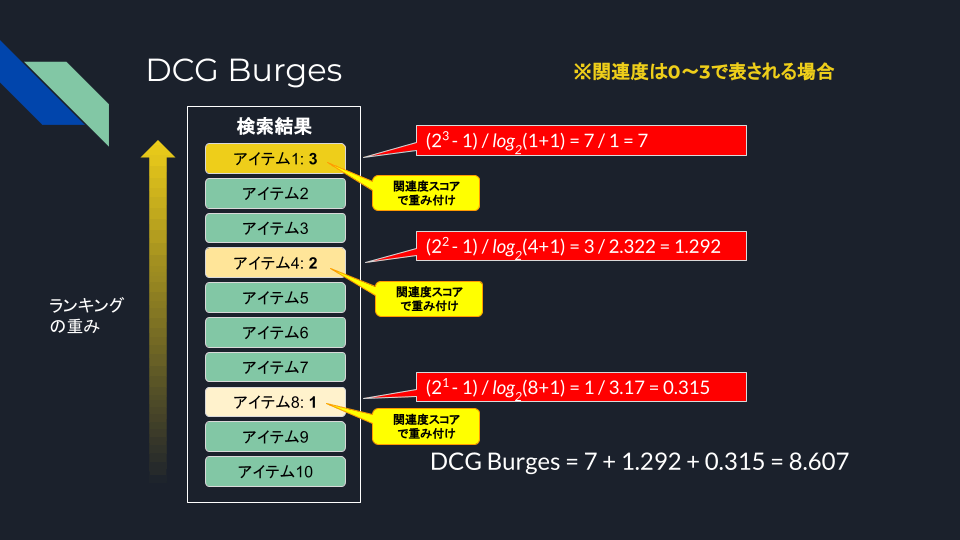
では実際にこの違いはどういうところに影響するのか？という例として、以下の記事がとてもわかりやすかった。

上記の例を実際にranxで試してみる。

関連度が高いものから順に並ぶ、理想的なランキングの場合

from ranx import Qrels, Run, compare

qrels1_dict = {
    "q_1": {
        "d_1": 5,
        "d_2": 3,
        "d_3": 3,
        "d_4": 3,
        "d_5": 3,
        "d_6": 3,
    },
}

qrels1 = Qrels(qrels1_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_2": 0.95,
        "d_3": 0.9,
        "d_4": 0.85,
        "d_5": 0.8,
        "d_6": 0.75,
        "d_7": 0.7,
        "d_8": 0.65,
        "d_9": 0.6,
        "d_10": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test")

report = compare(
    qrels=qrels1,
    runs=[run1],
    metrics=["dcg", "ndcg", "dcg_burges", "ndcg_burges"],
    max_p=0.01
)
print(report)

#    Model        DCG    NDCG    DCG Burges    NDCG Burges
---  --------  ------  ------  ------------  -------------
a    run_test  11.914       1        47.133              1

DCGの値は異なるが、NDCGについては共に1という理想的な状態であることがわかる。

では次。そこそこ関連度が高いものが上位に来ているが、最も高い関連度のものが低かった場合。

from ranx import Qrels, Run, compare

qrels1_dict = {
    "q_1": {
        "d_1": 5,
        "d_2": 3,
        "d_3": 3,
        "d_4": 3,
        "d_5": 3,
        "d_6": 3,
    },
}

qrels1 = Qrels(qrels1_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_2": 1,
        "d_3": 0.95,
        "d_4": 0.9,
        "d_5": 0.85,
        "d_6": 0.8,
        "d_7": 0.75,
        "d_8": 0.7,
        "d_9": 0.65,
        "d_10": 0.6,
        "d_1": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test")

report = compare(
    qrels=qrels1,
    runs=[run1],
    metrics=["dcg", "ndcg", "dcg_burges", "ndcg_burges"],
    max_p=0.01
)
print(report)

#    Model        DCG    NDCG    DCG Burges    NDCG Burges
---  --------  ------  ------  ------------  -------------
a    run_test  10.291   0.864          29.6          0.628

NDCGでは0.864と高い数字になっているが、NDCG Burgesは0.628とやや低めの数字になる。

では次。最も高い関連度のものが最上位に来て、そこそこの関連度のものが低かった場合。

from ranx import Qrels, Run, compare

qrels1_dict = {
    "q_1": {
        "d_1": 5,
        "d_2": 3,
        "d_3": 3,
        "d_4": 3,
        "d_5": 3,
        "d_6": 3,
    },
}

qrels1 = Qrels(qrels1_dict, name="qrel_test")

run1_dict = {
    "q_1": {
        "d_1": 1,
        "d_7": 0.95,
        "d_8": 0.9,
        "d_9": 0.85,
        "d_10": 0.8,
        "d_2": 0.75,
        "d_3": 0.7,
        "d_4": 0.65,
        "d_5": 0.6,
        "d_6": 0.55,
    },
}

run1 = Run(run1_dict, name="run_test")

report = compare(
    qrels=qrels1,
    runs=[run1],
    metrics=["dcg", "ndcg", "dcg_burges", "ndcg_burges"],
    max_p=0.01
)
print(report)

#    Model       DCG    NDCG    DCG Burges    NDCG Burges
---  --------  -----  ------  ------------  -------------
a    run_test  9.785   0.821        42.166          0.895

こちらの場合は、NDCGはそれほど大きく変わらないけども、NDCG Burgesの方は大きく上がってNDCGよりも高くなっている。

要は、ランキングの順位にくわえて、関連度の高いものに大きな重みをつけるということになる。

kun432

RAGの評価でどの指標を採用すべきか？

まず、各評価指標が大まかに何を評価するのか？と分けてみる。ここで以下の記事を参考にしてみる。

RAGのretrievalにおける評価は、クエリに対して適切なコンテキストを取得できるかどうか。大きく分けると以下の2つになると思う。

網羅性の評価
- 上記の記事では「集合検索指標」とか「分類」とされている
- 適切なコンテキスト情報を、入力コンテキストサイズの制限がある中でいかにカバーできているか？
  - retrievalは通常top- $k$ で取得する。少なくともここに含まれる必要がある。
ランキングの評価
- より関連度の高いコンテキスト情報を、ランキングの上位に配置できているか？
- LLMはコンテキストの先頭（と末尾）の文章を重要視する
  - Lost in the Middle: How Language Models Use Long Contexts
  - 上記の解説記事
  - （末尾というのがややこしいが、少なくとも適切な関連度順に並んでいれば、順序を入れ替えるということはあとからでもできる）

あと、評価用データセットによっても変わってくると思う。通常RAGのコンテキストと評価用のクエリを作る流れとしてパッと思いつくのは、

ドキュメントをチャンク分割する
分割されたチャンクごとにクエリを生成させる

の流れ。この流れだと、クエリと関連コンテキストの1対1のペアを作るのはとても簡単だけど、複数のチャンクにまたがるようなクエリとか、さらに関連度のグラデーションを作るのは、それなりに手間がかかると思う。

個人的にシンプルなクエリ・関連コンテキストが1対1のペアからなる評価データを使う場合には、以下あたりをカバーしておけば、大雑把な評価はできると思う。

関連するコンテキストを拾えているか？
- Hits/Hit rate
- Recall
関連するコンテキストをランキング上位で拾えているか？
- MRR
- Rank-biased Precision
- MAP
- NDCG

ランキングの方は似たような評価になるものもある気がするので、もう少しそれぞれの意味合いを理解すれば減らせると思う。なんとなくMRRだけでも良い気がする。

ちなみに、こちらの方、RAG周りのテクニックをいろいろ試してその結果を公開されている方なのだけども、評価指標にはRecall/MRR/NDCGを使っている様子。

kun432

当然ながら、クエリが複数のコンテキストに紐づいているとか、関連度のグラデーションが設定できれば、より詳細な評価を行いやすいとは思うが、そういうデータを用意できるかどうかになる。

例えば、RAGの評価用ツールであるragasはテストデータ生成も行える（ただしこの機能はまだベータではなかろうか）のだけど、テストデータ生成時に以下の観点を設定できる。

Reasoning: 文章の論理関係の推論を必要とするような質問を生成する
Conditional: 条件的要素を質問に含めて複雑性を上げる
Multi-Context: 回答するには、複数の関連セクションからの情報を必要とするような、質問を生成する

上記のマルチコンテキストとかを使えばできそうな気もする。

あと、関連度みたいなものはrerankとか使ってできないかなーとか思ったりもする。

いずれにせよ、サポートされている評価指標をフルに使いこなすには、シンプルなテストデータ生成にひと手間加える必要はある。逆に言うとシンプルなテストデータで評価するならば、使う必要がない評価指標もあるということだと思っている。

kun432

どういう指標を使うべきか？については以下の記事も参考になる

kun432

評価データがシンプルな「クエリと合致するコンテキスト（ドキュメント）の1対1のペア」の場合、どの評価指標を「使わないべきか？」をChatGPTに聞いてみた。

User:
クエリと合致するコンテキスト（ドキュメント）のペアがあります。これを使って、検索の評価を行いたいと考えていますが、クエリとコンテキストは1対1のペアです。

以下の評価指標のうち、上記の条件にそぐわないものをリストアップしてください。

Hits
Hit Rate / Success
Precision
Recall
F1
R-Precision
Bpref
Rank-biased Precision
(Mean) Reciprocal Rank
(Mean) Average Precision
DCG
DCG Burges
NDCG
NDCG Burges

ChatGPT:
クエリとコンテキスト（ドキュメント）が1対1のペアで構成される検索評価の状況において、適さない評価指標を考える際には、それぞれの指標が何を測定し、どのような仮定に基づいているかを理解することが重要です。以下に、指定された条件にそぐわない可能性のある評価指標をリストアップし、その理由を説明します。

Recall:
再現率は、関連するドキュメントのうち、検索システムがどれだけ見つけられたかを測定します。しかし、クエリとコンテキストが1対1のペアである場合、各クエリに対して関連するドキュメントは1つのみとなり、再現率の計算は意味をなさない可能性があります。これは、再現率が関連ドキュメントの全体集合を前提としているためです。

F1:
F1スコアは、精度と再現率の調和平均です。再現率がこのシナリオに適していないため、F1スコアも同様に不適切と考えられます。

R-Precision:
R-精度は、関連するドキュメントの数がRであるときの上位Rドキュメントの中での関連ドキュメントの割合を測定します。1対1のペアリングでは、関連するドキュメントの総数が各クエリに対して1であるため、この指標の適用性が限られます。

(Mean) Average Precision (MAP):
平均精度の平均は、各クエリについて関連ドキュメントが見つかるたびに計算される精度の平均値を取ります。1対1のペアの場合、各クエリに対して関連するドキュメントが1つだけであるため、MAPの概念が適用しにくいです。

DCG Burges:
DCG (Discounted Cumulative Gain) は、ランキングの質を評価する指標ですが、"DCG Burges" は一般的な用語ではなく、DCGのバリエーションを指す可能性があります。ただし、DCGとその派生形態はランキングの上位にあるアイテムの重要性を重視するため、1対1のペアリングではそれほど関連性がありません。

NDCG Burges:
NDCG (Normalized Discounted Cumulative Gain) はDCGを正規化したもので、ランキングの質を評価しますが、"NDCG Burges" という用語も一般的ではなく、恐らくNDCGの特定の応用を指しています。NDCGもランキングに焦点を当てているため、1対1のペアリングには適していないかもしれません。

上記以外の指標は、1対1のクエリとドキュメントのペアリングで使用される場合にも有用であるか、または直接適用が可能です。たとえば、HitsやHit Rate/Successは、単一の正解ドキュメントが検索結果に存在するかどうかを測定するため、このシナリオに適しています。Precisionや(Mean) Reciprocal Rank、Rank-biased Precision、DCG、NDCGは、特定のドキュメントの位置や1つの正解の存在に基づいて評価を行うため、適用可能です。

User:
precision難しくないですかね？検索結果数（top-k）によって左右されますよね？

ChatGPT:
はい、おっしゃる通りで、精度（Precision）は検索結果の数（top-k）に大きく左右される評価指標です。精度は、検索結果として返されたドキュメントのうち、実際に関連するものの割合を測定します。したがって、検索結果の数が変わると、精度の値も変動します。

例えば、あるクエリに対して関連するドキュメントが1つだけ存在し、そのドキュメントが検索結果のトップに来た場合、top-1での精度は100%になります。しかし、もし検索結果がトップ5まで拡張され、残りの4つのドキュメントが関連性がない場合、精度は20%（1/5）に低下します。

このように、検索結果の範囲をどのように設定するか（つまり、top-kの値をどのように選ぶか）は、精度を評価する上で非常に重要です。特に、クエリとドキュメントが1対1のペアで構成される場合、検索システムがそのペアのドキュメントをどの位置にランキングするかによって、精度の値が大きく変わることがあります。

そのため、1対1のペアリングのコンテキストでは、精度を評価する際には、特定のtop-kの設定に注意を払う必要があります。また、このような状況では、(Mean) Reciprocal RankやRank-biased Precisionなど、ランキングの質全体を考慮する他の指標を併用することで、よりバランスの取れた評価が可能になります。

User:
あとrecallが駄目なのはちょっとわからないです。recallはtop-kに関係なく、合致するドキュメント数が母数になると思うので、悪くないと思うのですが

ChatGPT:
ご指摘の通り、再考する必要があります。再現率（Recall）は、実際に関連するドキュメントの中から、検索システムがどれだけのものを正しく検索できたかを測定する指標です。再現率の計算式は、関連するドキュメントが検索結果に現れる割合を示しています。したがって、全ての関連ドキュメントを検索結果として取得できた場合、再現率は100%になります。

私の前の説明では、クエリとコンテキストが1対1のペアである場合に再現率が適さないと誤って述べましたが、これは不正確でした。1対1のペアリングの状況で、各クエリに対して1つだけ関連ドキュメントが存在すると仮定すると、そのドキュメントが検索結果に含まれているかどうかだけが問題となります。この場合、検索結果にそのドキュメントが含まれていれば、再現率は100%になります。逆に、そのドキュメントが含まれていなければ、再現率は0%になります。

つまり、1対1のペアリングにおいては、各クエリに対して関連するドキュメントが1つだけ存在するという前提の下で、再現率は関連ドキュメントが検索結果に含まれるかどうか（つまり、検出されるかどうか）に基づいています。このシナリオでは、再現率は非常に単純化された形で適用され、各クエリに対する検索結果の有無のみを評価します。

この点を誤って説明したことをお詫び申し上げます。1対1のペアリングのコンテキストでは、再現率は関連ドキュメントが検索結果に正しく含まれているかどうかを評価する簡潔で直接的な方法を提供します。

User:
ただhitsやhit rateと何が違う、と言われると、差異は無いような気はしますね。

ChatGPT:
おっしゃる通りです。実際には、1対1のクエリとドキュメントのペアリングの文脈では、HitsやHit Rate（Success Rate）とRecallは非常に似た、あるいは実質的に同じ評価を提供することになります。これらの指標が似ている理由と、特定の文脈での使用における微妙な違いを掘り下げてみましょう。

HitsとHit Rate / Success Rate

Hits は、特定のクエリに対してシステムが関連ドキュメントを「ヒット」または見つけた回数を指します。1対1のペアリングでは、各クエリに対して関連ドキュメントが1つのみ存在するので、ヒットの有無が評価されます。

Hit Rate / Success Rate は、全クエリの中でシステムが関連ドキュメントを見つけた割合を指します。これは、成功した検索の割合を示し、1対1のペアリングでは、各クエリに対して正しいドキュメントが検索結果に含まれているかどうかに基づきます。

Recall

Recall は、全ての関連ドキュメントのうち、システムがどれだけ見つけ出したかを測定します。1対1のペアリングのケースでは、各クエリに対して1つの関連ドキュメントがあり、それが検索結果に含まれているかどうかを評価します。

差異の考察

1対1のペアリングでは、 Recall と Hits / Hit Rate は本質的に同じ情報を提供します。すなわち、システムが特定のクエリに対して正しいドキュメントを見つける能力を評価しています。

違いは、これらの用語が一般に使用される文脈によるものです。Recall は通常、検索されるべき関連ドキュメントの全体集合に対する指標として理解され、複数の関連ドキュメントが存在する可能性のある場合によく使用されます。一方で、Hits / Hit Rate は、特定のクエリに対する単一の成功した検索結果の有無に焦点を当てたより直感的な指標として捉えられることが多いです。

この文脈では、これらの指標が提供する情報の重複を認識し、適切な指標を選択する際には、その用語の一般的な使用法や評価の目的を考慮することが重要です。

このスクラップは2024/02/28にクローズされました