Zenn
📖

ゼロからつくるDeepLearning 2 格闘日誌5/30 5章

に公開
ディープラーニング
rnn
tech

ゼロから作るDeep Learning 2を友達と読んでいます．
本記事は本書の内容かつ，留学中の授業内の内容のノートです．
読者対象はゼロから作るDeep Learning 実装が終わったくらいの方，Deep Learning 2を読んでいる方です．

5章　RNN

・FFNNの問題点とRNNの登場
(FFNNの問題点)時系列データ(Sequence)を扱えない．単純なFFNNは，時系列データを十分に学習できない．
(理由)FFNNではそれぞれのニューロンの活性化が一度しか起こらない
→RNNでは出力をもう一度入力に加えることで，
・繰り返し的に学習
・任意長(variable-length)のsequenceを処理できる．

5.1 確率と言語モデル

word2vecの復習
言語を確率として扱う言語モデルについて説明

5.1.1 word2vecを確率の観点から眺める

  • ターゲット：中央の注目している単語
  • コンテキスト：ターゲットの周囲の単語
    CBOWモデルの行うこと：コンテキストw_{t-1},w_{t+1}からターゲットw_tを予測すること
P(w_t|w_{t-1},w_{t+1})．

コンテキストを左側だけに限定すると，

P(w_t|w_{t-2},w_{t-1})．

CBOWモデルでは，以下の損失関数Lを最小化するような(=教師データと同じ結果を出力するような)重みパラメータに調整すれば，その副産物として単語の分散表現が得られる．

L = - \log{P(w_t|w_{t-2},w_{t-1})}

CBOWモデルの主目的の，「コンテキストからターゲットを推測すること」は何かの役に立つのか？
次章ではCBOWモデルの限界について述べる．

5.1.2 言語モデル

Langage model(言語モデル)：単語の並びに対して確率を与える(マルコフ決定過程であるとは限らない．)
言語モデルの適用例：機械翻訳や音声認識，新たな文章の生成(これは7章で取り上げる)
単語w_1,...w_mがこの順番で出現する確率P(w_1,...,w_m)として，

P(w_1,...,w_m) = P(w_m|w_1,...,w_{m-1})P(w_{m-1}|w_1,...,w_{m-2})...P(w_3|w_1,w_2)P(w_2|w_1)P(w_1)
=\prod_{t=1}^m P(w_t|w_1,...,w_{t-1})

この結果は確率の情報定理P(A,B)=P(A|B)P(B)から再帰的に導ける
Conditional Language model(条件付言語モデル)：P(w_t|w_1,...,w_{t-1})を出力するモデル

5.1.3 CBOWモデルを言語モデルに？

コンテキストを左側の2つに限定し，近似を行うと

P(w_1,...,w_m) =\prod_{t=1}^m P(w_t|w_1,...,w_{t-1})\approx\prod_{t=1}^m P(w_t|w_{t-2},w_{t-1})．

マルコフ性：未来の状態が現在の状態だけに依存して決まる
N階マルコフ連鎖：ある事象の確率がその直前のN個の事象のみによって決まる
ここでは2階マルコフ連鎖といえる

CBOWモデルのコンテキストサイズを大きくすることは解決策になりうるか？

  • 任意の文字数の入力を受け付けることはできない(固定長のウィンドウサイズ)
  • コンテキスト内の単語の並びが無視される(本書より．これは実装の問題であり，Continuousという名前の通り実装によっては順番を考慮した実装も可能．本書のCBOWモデルは順番は無視される)

5.2 RNNとは

Reccurent：何度も繰り返し起こること
Reccurent Neural Network(RNN，再帰ニューラルネットワーク)cf.Recursive Neural Network,木構造のデータ処理のためのネットワークで別物

5.2.1 循環するニューラルネットワーク

(RNNの特徴)：ループした経路を持つ
過去の情報を次の出力に受け継げる．

5.2.2 ループの展開

\bf{W}_hを時刻t-1における出力を時刻tにおける入力に変換する
\bm{h_{t-1}}，\bm{x_t}は行(Row)ベクトルとする．
ちなみにRow Vector 行ベクトル，Column 列ベクトルは覚え方があるので，理工系の人は特に覚えておいたほうがいい．
https://lambdalisue.hatenablog.com/entry/2013/07/18/134507
時刻tにおける\bm{h}_tは，

\bm{h}_t = \tanh(\bm{h}_{t-1}\bf{W}_h +\bm{x}_t\bf{W}_x+\bm{b})

問題：\bm{h}_tはどのようなベクトル？
この式を読み解くと、過去の出力と現在の入力から正しそうな出力を計算するように学習が行われそうであることが分かる．

5.2.3 Backpropagation Thorough Time

BPTT：Backpropagation Thorough Time，時間方向に展開したニューラルネットワークの誤差逆伝播法
問題点：長い時系列データを学習する際の計算リソースが増加する

5.2.4 Truncated BPTT

Truncated BPTT：切り取った小さなネットワークに対して誤差逆伝播法を実行する．
ブロック内でのみ誤差逆伝播法を行う(ブロック間をつなぐ伝播は無視される)それにより未来のデータについて考慮することなく、並列処理的に計算できることが分かる．

5.2.5 Truncated BPTTのミニバッチ学習

Truncated BPTTにおけるミニバッチ学習方法について説明する．例えば，100000単語の文章データを考える．1単位あたりを100単語のシーケンスで区切ると，1000行100列のデータを成型できる．そして1000個のRNNマシンそれぞれに，100単語のシークエンスを与えて伝播を行うのである．(実際には，一つの変数にテンソル型でデータを与え，GPUがあれば並列で計算することになる．)

5.3 RNNの実装

RNNを実装するには，固定長Tだけ横方向にのびる，パラメータを共有したニューラルネットワークを作ればよい．

5.3.1 RNNレイヤの実装

RNNの順伝播は以下の式で表される．

\bm{h}_t = \tanh(\bm{h}_{t-1}\bf{W}_h +\bm{x}_t\bf{W}_x+\bm{b})
time_layers.py
class RNN:
    def __init__(self, Wx, Wh, b):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like[Wx],np.zeros_like[Wh]]
        self.cache = None
    def forward(self, x, h_prev):
        Wx, Wh, b = self.params
        t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
        h_next = np.tanh(t)
        self.cache = (x, h_prev, h_next)

self.cacheでh_prevとh_nextをキャッシュする

5.3.2 Time RNNレイヤの実装

common/time_layers.py
import numpy as np
class TimeRNN:
    def __init__(self,Wx,Wh,b,stateful=False):
        self.params = [Wx, Wh, b]
        self.grads = [np.zeros_like(Wx),np.zeros_like(Wh),np.zeros_like(b)]
        self.layers = None
        self.h, self.dh = None, None
        self.stateful = stateful
    
    def set_state(self, h):
        self.h = h

    def reset_state(self, h):
        self.h = None

set_state, reset_stateで隠れ状態hの状態を維持するかどうか決める．これは手動で隠れ状態の保持の有無を設定するため．

common/time_layers.py

    def forward(self,xs):
        #xsは3次元テンソル，入力列のバッチ．
        Wx, Wh, b = self.params
        N, T, D = xs.shape
        #バッチサイズをN個，T個のRNNレイヤ(入力ベクトル数)，入力ベクトルの次元数D
        D, H = Wx.shape
        
        self.layers[]
        hs = np.empty((N,T,H),dtype = 'f')

        if not self.stateful or self.h is None:
            self.h = np.zeros((N,H),dtype='f')
        
        for t in range(T):
            layer = RNN(*self.params)
            self.h = layer.forward(xs[:,t,:],self.h)
            hs[:, t, :] = self.h
            self.layers.append(layer)    
        
        return hs

forward内でRNNレイヤを作り出すのには，次のような設計上の理由が挙げられる：

  • メモリを専有することを防ぐため
  • forwardメソッドを実行するときになって初めてその長さが分かる(その時々で変わりうる．(ex.最後のバッチなどは，長さが短いことが起こりうる))
  • レイヤの再利用が不可能：毎回異なる中間状態hを持つため，TimeRNNは再利用できない(毎回Wx,Whを入れて新しいものを作り出す)
common/time_layers.py
def backward(self, dhs):
        Wx, Wh, b = self.params
        N, T, H = dhs.shape
        D, H = Wx.shape

        dxs = np.empty((N, T, D),dtype='f')
        dh = 0
        grads = [0, 0, 0]
        for t in reversed(range(T)): 
            #reversed:逆方向から勾配伝播
            layer = self.layers[t]
            dx, dh = layer.backward(dhs[:,t,:] + dh)
            dxs[:, t, :] = dx

            for i, grad in enumerate(layer.grads):
                #gradsの中身を順番に取り出す．iはインデックス
                grads[i] += grad
            
        for i, grad in enumerate(grads):
            self.grads[i][...] = grad
            #self.gradsはoptimizerに参照される可能性があるのでin-placeで中身だけ差し替え
        self.dh = dh

5.4 時系列データを扱うレイヤの実装

RNNLM(Language Model)：RNNを用いた言語モデル

5.4.1 RNNLMの全体図

省略　本誌参照．
input(文章)→Embedding→RNN↓→Affine→Softmax→output(ある単語の確率)

5.4.2 Timeレイヤの実装

Timeレイヤは，TimeRNNから出力された時系列データをまとめて処理するレイヤのことである．

  • Time Affine
  • Time Softmax with Loss
    これについては，本誌付属のレイヤを使用する．

5.5 RNNLMの学習と評価

RNNLMの実装と評価を行う

5.5.1 RNNLMの実装

SimpleRNNLMの実装．
Time Embedding→Time RNN→Time Affine→Time Softmax with Loss
以下にSimpleRNNLMの実装を示す．まずは初期化

5_5_1simple_rnnlm.py
class Simple_Rnnlm:
    def __init__(self, vocab_size, wordvec_size, hidden_size):
        """
        Initializes the Simple RNN language model.

        Parameters
        ----------
        vocab_size : int
            The size of the vocabulary (number of unique words).
        wordvec_size : int
            The size of the word embedding vectors.
        hidden_size : int
            The number of hidden units in the RNN layer.

        Notes
        -----
        - np.random.randn is aliased as rn for convenience.
        - The embedding weight matrix `embed_W` is initialized with random values
          from a normal distribution, scaled by 1/100, and cast to float32 type.

        """
        V, D, H = vocab_size, wordvec_size, hidden_size
        rn = np.random.randn
        #np.random.randnのエイリアス設定

        # 重みの初期化 V→D→H
        # astype('f') :NumPy 配列のデータ型を float32（32ビット浮動小数点数）に変換
        embed_W = (rn(V, D) /100).astype('f')
        rnn_Wx = (rn(D,H) /np.sqrt(D)).astype('f')
        rnn_Wh = (rn(H,H) /np.sqrt(H)).astype('f')
        rnn_b = np.zeros(H).astype('f')
        #H→V
        affine_W = (rn(H,V)/np.sqrt(H)).astype('f')
        affine_b = np.zeros(V).astype('f')

        # レイヤの生成
        self.layers [
            TimeEmbedding(embed_W),
            TimeRNN(rnn_Wx, rnn_Wh, rnn_b, stateful=True),
            TimeAffine(affine_W,affine_b)
        ]
        self.loss_layer = TimeSoftmaxWithLoss()
        self.rnn_layer = self.layers[1] # あとで参照するためのエイリアス

        # すべての重みと勾配をリストにまとめる
        self.params, self.grads = [], []
        for layer in self.layers:
            self.params += layer.params
            self.grads += layer.grads

個人的に，よく使う関数に省略名(エイリアス)を設定しているのをマネしたいと思った．

関数のエイリアス設定
rn = np.random.randn
        #np.random.randnのエイリアス設定

次に，順伝播逆伝播reset_state：

5_5_1simple_rnnlm.py
    def forward(self,xs,ts):
        for layer in self.layers:
            xs = layer.forward(xs)
        loss = self.loss_layer.forward(xs, ts)
        return loss
    
    def backward(self,dout=1):
        dout = self.loss_layer.backward(dout)   
        for layer in reversed(self.layers):
            dout = layer.backward(dout)
        return dout
    
    def reset_state(self):
        self.rnn_layer.reset_state()

5.5.2 言語モデルの評価

perplexity(パープレキシティ)：言語モデルの予測性能の良さを評価する指標．単語の予測確率の逆数を示す．

  • perplexの意味：曖昧さ
    モデルが自信をもって予測できない(=予測確率が分散している)と高い値になる．
  • perplexityの直感的解釈：文奇数
    次に出現しうる単語の候補の数．(ex. perplexity = 5の時，最大の予測確率が0.2であり，最大で5個の等しい予測確率を持ちうる．)
    (入力データが複数の場合のperplexity)：
    Lを損失関数として，
perplexity = e^L

5.5.3 RNNLMの学習コード

学習コードは本書参照．

実行結果
corpus size: 1000, vocabulary size: 418
epoch 1 | perplexity 403.49
epoch 2 | perplexity 292.84
epoch 3 | perplexity 232.05
epoch 4 | perplexity 219.81
epoch 5 | perplexity 208.32
(Truncated by author)
epoch 98 | perplexity 5.05
epoch 99 | perplexity 4.96
epoch 100 | perplexity 4.98

epoch_list = [i for i in range(max_epoch)]
#plot
plt.plot(epoch_list,ppl_list)
plt.xlabel("epochs")
plt.ylabel("perplexity")
plt.show()

以下にplotした結果を示す．

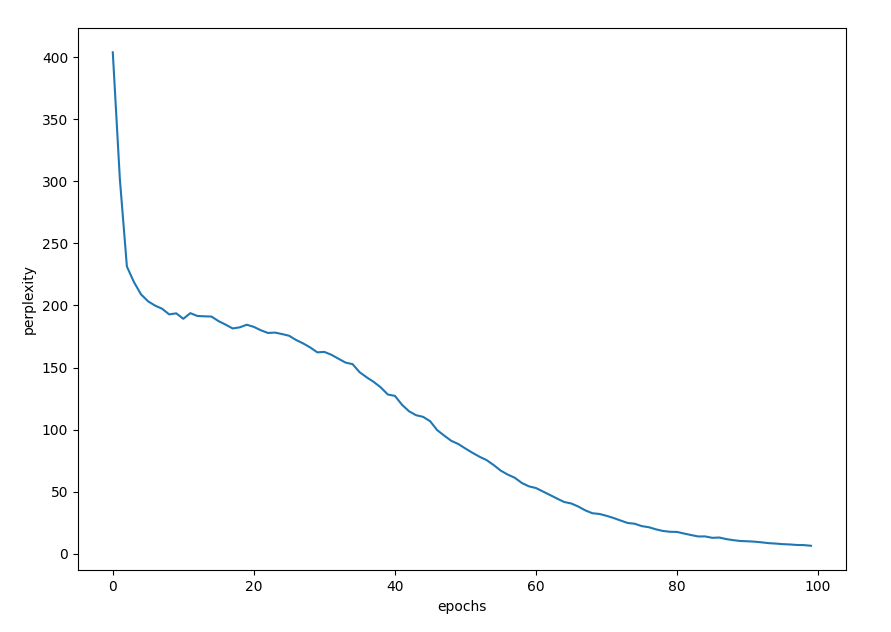
かなりperplexityが1に近づいていることが分かる．

5.5.4 RNNLMのTrainerクラス

今後は本書で用意されたTrainerクラスを使う(一連の順伝播逆伝播、重み更新，perplexity評価を行う)

5.6 まとめ

  • RNNのループ経路により隠れ状態を内部に記憶できる
  • BPTT(Back Propagation Through Time)
  • Truncated BPTT(隠れ層の逆伝播のつながりのみ分断する)
  • RNNはこれまで登場した単語の情報を記憶できる

Discussion