強化学習アルゴリズムの色々な分類

この記事について

この記事は自分の Notion で編集したものを zenn のフォーマットに書き換えたものです。

この記事を書くに至った経緯

飛ばしてもらって構いません。

2024年2月、自分は東京大学大学院工学系研究科にて、強化学習（Reinforcement Learning; 以降RL）を使った修士論文を提出しました。
学部時代とは畑の違う学科（専攻）だったので、RLや対象とする工学問題の勉強を一から（さらに修士1年間遊んだので実質1年で）したわけですが、RLは機械学習の中ではあまり参考になる日本語文献が多くない印象がありました。
ものの「AI入門」的な本でも、教師あり学習が50ページぐらい書かれているならRLは5ページ足らずで基本的な用語をさらっと紹介しているだけといった印象です。

ネット上には各用語や基礎理論の解説などはあるのですが、それぞれ散逸していて、全体観を掴むのに苦労しました。
「アルゴリズムまとめ」的な有名記事も一通り見ましたが、一側面的な分類が多く、「このアルゴリズムって〇〇法でもあってxx法でもあるんか？」や「A手法は、B手法のサブセットなんか？」、「このテクニックはこのアルゴリズムでは使えないんか？」と、かなり混乱したものです。
たとえば、「状態価値」「Q学習」「方策ベース」「TD法」「ε-greedy」といった用語は、異なる視点からのRLの用語ですが、それぞれの関係を説明できるでしょうか？

自分はこういった用語を Notion にまとめていくうちに、RLを多面的に捉えることができ、その輪郭がわかってきました。
散逸的にも各用語をブワーッと勉強して、それが脳内で繋がるのを待つというのも（特に新しい分野では）良い方法だと思いますが、脳は階層的に整理された情報を好むと思うので、分類や階層に注目すると理解が早いです（実際、「繋がる」は両者の関係性の認識なので、分類や階層、因果などについての気づきが大半かと思います）。

長くなりましたが、この記事がRLを勉強する人の地図や引き出しになってくれればと思います。

まとめ

アルゴリズム	価値ベース・方策ベース	価値関数の更新法	方策オン・オフ	モデルベース・モデルフリー
Q-learning	価値ベース	TD法	方策オフ	モデルフリー
SARSA	価値ベース	TD法	方策オン	モデルフリー
DQN系	価値ベース	TD法	方策オフ	モデルフリー
REINFORCE	方策ベース	（方策をモンテカルロ法で更新）	方策オン	モデルフリー
A3C, A2C, TRPO, PPO（Actor-Critic）	方策ベース	TD法	方策オン	モデルフリー
DPG, DDPG（Actor-Critic）	方策ベース	TD法	方策オフ	モデルフリー

テクニック	価値ベース・方策ベース	方策オン・オフ	モデルベース・モデルフリー
ε-greedy	価値ベース
target-network		方策オフ
experience replay		方策オフ

この記事の構成

大きな分類から入って、徐々にレイヤーを降りていきます。特に位置付けのわからないワードを見たいだけあれば、ページ内検索などで辞書のようにも使っていただけるかと思います。

RLの勉強の最初のとっかかりになることを意識しているので、知っておくべき用語は使いつつ、できるだけ平易な文章で書いており、数式の展開などは省略しています。

強化学習の基礎と分類

機械学習全体における強化学習

まずはRL全体を機械学習の文脈に位置付けたいと思います。

機械学習の学習法による分類は以下の3つからなります。

• 教師あり学習
• 教師なし学習
• 強化学習

つまり、RLは教師あり学習や教師なし学習と並列です。

単純な教師あり学習との違いは、以下のようなものが挙げれらるでしょう。詳しくは次の節で説明します。

• 長期的な視点も学習できる
• 人間が用意するのはデータではなくルール

ちなみに、機械学習全体は、AI に包含されます。
機械学習でない AI には、たとえば「エキスパートシステム」などがあるようです。ここら辺は割愛します。
よって AI を分解すると、次のようになります。
AI
├ …
└ 機械学習
　 ├ 教師あり学習
　 ├ 教師なし学習
　└ 強化学習

さらにちなみに、機械学習はモデルによっても分類されます。
これは機械学習という言葉の「機械」に当てはまると考えると良いでしょう。
たとえば、単純には数式です。二値分類モデルは直線を境界として分類でき、その直線の式の重み（係数）を学習によって獲得するわけです。
昨今の AI ブームの礎の深層学習もこのモデルによる分類の1つと言えます。

強化学習の基礎と構成要素（基礎用語）

RL自体の位置付けを見たところで、RLの中に入っていきます。

よくRLは「エージェントが環境と相互作用し、その結果として得られる報酬を最大化するように行動することを学習するもの」のような説明がされます。

以下の図に沿ってRLのフローを一度おさらいします。各用語は後にまとめてあります。RLはゲームに使われることが多いので、用語ではこれにも準えて書いています。

自分の修士論文より引用

1. 時刻 $t$ において、状態をもとにエージェントが⽅策 $\pi$ により⾏動 $a_t$ を決める

2. $a_t$ が環境に渡され、状態遷移関数 $P$ によって $t+1$ の状態 $s_{t+1}$ が決まる

3. 行動の結果を元に報酬関数 $R$ によって報酬 $r_t$ を計算する

4. $s_{t+1}$ と $r_t$ がエージェントに渡され、これらと前の状態⾏動対などももとに、学習アルゴリズムが⽅策を更新する

   後述の価値ベースのアルゴリズムでは方策は一定だが、簡単のために価値関数の更新も含めて方策の更新とした。

5. $s_{t+1}$ を元に、$\pi$ により次の行動 $a_{t+1}$ を決める

実際には学習のタイミングは毎回行動後とは限りませんが、おおまかには以上を繰り返して、最適な方策を学習します。

このような全体像を踏まえると、以下の用語の関係を捉えやすくなったかと思います。

• エージェント

  ⾏動主体のことで環境と相互作⽤するもの。方策をもつ。ゲームのプレイヤー。

• 環境

  状態遷移関数と報酬関数からなるシステム。これらは、基本的にマルコフ決定過程である必要がある。ゲーム自体。プレイヤーから見ればゲーム機、ゲームのルール。

• エピソード

  行動を繰り返す一連の時間のまとまり。この期間で得られた報酬の累積を最大化することを目指す。行動を行うタイミングを1つのタイムステップと考えると、何ステップ行動した時点で評価するか、というもの。ゲームでいうなら、制限時間みたいなもの。

• 状態

  エージェントに知覚される環境の様⼦。ゲームでは、ゲーム画面や自分の残りHPなどの情報。

• 方策

  ⾏動を決定するルール。ゲームで言うなら「相手が攻撃してきたら避ける」「この攻撃の次はこの攻撃をする」など、プレイヤーの色が出る状況ごとの意思決定ルール。

• 行動

  環境に渡されるエージェントの働きかけ。ゲームで言うなら「避ける」「攻撃する」など。

• 状態遷移関数

  エージェントの⾏動と前時点の状態をもとに次の状態を返す関数。一般に確率的。ゲームで言うなら「上ボタンが押されたら画面を上に動かす」「氷の上を歩いたら20%で滑る」というルール。

• 報酬

  ⼀般に⾏動の結果が望ましいほど⼤きい値を取るものであり、
  エージェントはこれを最⼤化することを⽬指して⾏動する。

  ここでは、行動してすぐに報酬をもらっているので、特に即時報酬と呼ぶ。即時報酬でないものは、例えばエピソードの最後に一度だけもらえる報酬。

  ゲームでいうならスコア。

• 報酬関数

  報酬を計算する関数。一般に報酬の計算に使われる行動の結果 = 状態 とは限らない。そのため厳密には $R$ の入力は一般には $P$ の出力ではないので、図中では破線で示した。

  これもゲームのルールの一部であり、上記の話はゲームのスコアをプレイヤーに公開した情報（= 状態）以外からも計算して良い、ということ。

価値

価値はなんだかんだ色んな説明をする上で避けられないので書いておきます。

ちょっとだけ数式を使った説明は付録に書いておきます。ここでは簡単な説明にとどめます。

RLでは、エピソードで得られる報酬の累積を最大化することを目指します。例えば、目先では損をしても長期的には得になる行動を選択できるのです。この点で教師あり学習とは異なります。

さて、そのような行動を取るために、エージェントはある時点で「これから先どれだけ報酬を得られるか」を考えると良さそうです。

簡単にいうと、この「『これから先得られる報酬の累積』の期待値」が価値です。

価値には、状態価値と行動価値がありますが、これらはどの時点からみたかという違いです。図で見てみます。

離散的な行動・状態を考えます。つまり、以下のように状態も行動も枝分かれで考えられる問題です。

自分の修士論文より引用

図では、状態 $s$ から、方策 $\pi$ によって行動 $a$ を選んで、その行動を受けて状態遷移関数 $p_T$ で次の状態 $s'$ に遷移しています。

このような段階を踏んだ時、状態価値、行動価値は以下のように対応します。

状態価値を $V^\pi$、行動価値を $Q^\pi$ で表しています。
$V^\pi$ はある「状態にいる時」から見た価値、 $Q^\pi$ はある「行動をとった時」から見た価値、ということになります。
添字 $\pi$ がつくのは、その時点以降どれだけ報酬が得られるかは方策によるからです。

自分の修士論文より引用

この価値は、上に書いてあるように、関数で書けます。$V^\pi$ は $s$ の、$Q^\pi$ は $s, a$ の関数です。これをある時点の値である価値と区別して価値関数と呼ぶことにします。

とりあえず価値についてはここまでわかっておけば大丈夫かと思います。

アルゴリズム分類法

では本題です。アルゴリズムの分類の切り口に沿って、その分類に当てはまる代表的な（最初に紹介されるような）アルゴリズムを紹介します。モダンなアルゴリズムについては省略しています。

価値ベース・方策ベース

• 各分類の紹介

  • 価値ベース

    価値の良い近似を得るというアプローチ（一般に価値の真の値を知ることは難しい）
    つまり価値関数を学習する

    この際の方策は基本的に「価値が最大になる行動を選択する」となる

    連続行動空間で使えない

    代表的なアルゴリズム：Q学習、SARSA、DQN系

  • 方策ベース

    方策を直接学習する

    連続行動空間でも使える

    代表的なアルゴリズム：REINFORCE、Actor-Critic系

• 価値ベース

  価値ベースでは方策が一定であることに注意してください。「強化学習がより良い行動を取るために学習する」ものであることを踏まえると、この「方策を更新しない」というのは一見不思議に見えます。ただ、「毎回どの行動が最も価値が高いかを考えて行動する」というのは、直観的にはわかりやすいかと思います。価値には長期的な視点が含まれていますので、毎回価値だけで決めちゃっていいわけです。

  ここでは具体的なアルゴリズムとして、 Q学習と DQN系を紹介します。

  • Q学習

    行動価値 $Q$ を関数近似するアルゴリズムです

    簡単な場合には、状態と行動全パターンを並べて表を作って、各組み合わせの行動価値を埋め、学習にしたがってこの値を更新する

    普通、RLで扱う問題は状態空間と行動空間は大きく、組み合わせが爆発する
    そこで、表の代わりの関数近似としてディープニューラルネット（DNN: Deep Neural Net）を使った深層Q学習を使う

  • 深層Q学習

    深層学習の手法に則って、深層Qネットワーク（DQN: Deep Q Network）を学習する
    （学習アルゴリズムとしては Deep Q-learinig が正しいのですが、今回は簡単のために学習アルゴリズムも DQN と呼んでいます）

    Q学習と区別してわざわざDQNと呼ぶのは、関数近似にDNN を使う以外にも色んな学習テクニックを使うから

• 方策ベース

  方策ベースでは、直接方策を関数近似します。方策は状態を引数として各行動の確率を返すので、そのような関数近似を学習するわけです。

  学習、つまり方策を近似した関数のパラメータ $\theta$ の更新には、機械学習でお馴染みの勾配を使います。目的関数には状態価値を使います（ここでは $J$ ）。状態価値を最大化するようにパラメータを更新するので、勾配上昇です。
  （一般的な機械学習では、損失を最小化するように更新するので、勾配降下）

  $$\theta \leftarrow \theta + \alpha \nabla_\theta J(\theta) \\$$

  この勾配 $\nabla _\theta J$ は、方策勾配定理から得られます。特別にこんな名前がついているのは、この条件下では勾配が以下の式で書けるからです。

  （自分が昔書いた導出の手書きを付録に載せます）

  $$\nabla_\theta J(\theta)=\mathbb{E}_{\pi_\theta}\left[\nabla_\theta \log \pi_\theta(a \mid s) Q^{\pi_\theta}(s, a)\right]$$

  ここでは REINFORCE と、Actor-Critic を紹介します。

  • REINFORCE

    勾配は解析的には求められないので、特定の回数エピソードをこなして得られたサンプルを使って状態価値の勾配を近似する

    ここで2つの工夫をする

    • ベースラインの導入

      状態によって決まる値で、サンプルの平均報酬

      分散を小さくする効果がある

    • $Q^{\pi_\theta}$ を即時報酬で近似する

      $Q^{\pi_\theta}$ はわからないため

  • Actor-Critic

    Critic という価値関数を学習するモデルと、Actor という方策を学習するモデルの2つを使う
    （実際に行動する actor は方策ベースで学習しているため、一般的には方策ベースに分類される）

    Critic は価値ベースで学習する

    Actor がとった行動の結果の価値を critic が算出し、actor はその価値を最大化する行動を取るように学習する（ここが方策ベース）

「価値ベースでは連続行動空間が扱えない」とは
価値ベースのアルゴリズムは、行動を選択するために全ての可能な行動を確認する必要があります。
この時、行動が連続空間例えば $-1 <a< 1$ だと、行動$0.999$ の価値、$0.998$ の価値…と計算するのは大変そうですし、そもそもここでは $0.001$ で離散化してしまっています。
方策ベースでは、方策関数は行動を直接出力するものであり、これを連続値にしてもいいので、連続行動空間でも使えるわけです。

方策ベースで連続行動空間を扱う際
では、実際に方策ベースで連続行動空間を扱う時のことを考えます。
ここで１つ工夫があります。一般に方策は確率的に行動を決めるものでした。たとえば方策関数がDNNであることを考えてください。同じ状態をDNNに入力すると、毎回同じ値を出力してしまって確率的になりません。では連続値の行動を確率的に出すためにはどうしたらいいでしょうか。
答えは、方策の出力を確率分布と解釈する、です。分布の種類は一般には正規分布を想定します。確率分布はパラメータで決められます。正規分布の場合は平均と標準偏差です。
方策の出力はこれらのパラメータである（つまりここでは平均と標準偏差を出力する）と解釈すれば、方策の出力と分布が対応します。
そしてこの分布から行動をサンプリングすることで、確率的な行動ができるわけです。

価値関数の更新法による分類

方策ベースでは方策の更新は方策勾配と決まっていたのに対し、価値ベースのアルゴリズムは価値関数の更新法によっても分類できます。

• 各分類の紹介

  • モンテカルロ法

    エピソードの終了まで行動し、実際に得られた報酬のみを使って更新する

    エピソードが終わるまで更新できず、学習が遅くなる

    （代表的なアルゴリズム：REINFORCE、価値関数ではなく方策をモンテカルロ法で更新する）

  • TD法

    次のステップでの価値の推定値を使って現在の価値の推定値を更新する

    エピソード終了を待たずとも更新できるが、特に初期に誤った推定値をすると、誤った方向に学習が進む可能性もある

    （厳密には、これは TD(0) であり、何ステップ先まで考慮するかを $\lambda$ で表して TD(λ) という）

    代表的なアルゴリズム：Q学習、SARSA、DQN、actor-critic

    ちなみに、ある状態・行動の価値の推定値を、他の状態・高度の価値の推定値を使って更新することをブートストラップというそうです。

• Q学習系の更新法

  大きな分類的には上のようなものがありますが、Q学習系のアルゴリズムはそれぞれに更新法の特色があります。ここら辺はよくわからなくてつまづきました。

  更新式は似た形が多いです。なぜこのような形になるかは、付録の「価値」を見てみてください。

  • Q学習

    $$Q(s, a) \leftarrow Q(s, a)+\alpha\left\{r+\gamma \max _{a_{next}} Q\left(s^{\prime}, a_{next}\right)-Q(s, a)\right\}$$

    ここで、$s', a_{next}$ は次の状態とその状態で取りうる⾏動、$r$ は⾏動 $a$を取って得られる報酬、$\alpha$ は更新率。

    次の状態 $s'$ でとりうる全ての⾏動について $Q$ 値の推測値を計算し、最⼤のものを使って現在の $Q$ 値の推測値を更新する、という意味。

  • SARSA

    $$Q(s, a) \leftarrow Q(s, a)+\alpha\left\{r+\gamma Q\left(s^{\prime}, a^{\prime}\right)-Q(s, a)\right\}$$

    ここで $s', a'$ は実際の次の状態と実際の次の行動。

    つまり実際にとった行動から算出したQ値の推測値 $Q(s', a')$ を使って更新する。

  • DQN

    深層学習なので勾配降下法で更新するわけだが、その損失関数は

    $$L_i\left(\theta_i\right)=\mathbb{E}\left[\left(y_i-Q\left(s, a ; \theta_i\right)\right)^2\right] \\ y_i=\mathbb{E}\left[r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_{i-1}\right)\right]$$

    ここで、$i$ は学習のイテレーション数を表す。つまり、教師信号は学習回数が1つ少ない時のネットワークによる予測を使って作られている。これについては「学習テクニック」の章で触れる

• DQN の派生系

  ついでにDQNの派生系のアルゴリズムについてもいくつかここで触れておきます。後に紹介する事項と比較することで理解を助けるものたちです。

  • Double DQN

    行動選択をするためのネットワークと、Q値の評価をするためのネットワークを別にする。

    これらのネットワークが同じ場合に、特定の条件で⾏動価値を過⼤評価するという課題を解決するために提案された。

  • Dueling Network

    状態価値を学習するネットワークと、「その状態においてある⾏動が他の⾏動よりもどれだけ優れているか」の指標である advantage を学習するネットワークの２つを学習させ、Q を算出する。 Advantage は以下の式で定義される。

    $$A^\pi(s, a) = Q^\pi(s, a) - V^\pi(s)$$

    例えばどのような⾏動をとっても Q 値に差が出ない場合などで特に有⽤。

方策オン・方策オフ

DQN 系の紹介でちょっと出てきましが、個人的に強化学習で難しく感じたものの1つに、「学習で更新する方策」と「学習用データを集める時の行動方策（探索方策）」の違いがあります。これらの方策が同じかどうかという分類です。

方策オンか方策オフかは、教師信号を作る時に使う行動が、探索方策によるものと同じである（必要がある）かどうかと言えそうです。
この視点の方が具体的に使う場合には重要で、「学習テクニック」でまた出てきます。

• 各分類の紹介

  • 方策オン

    学習する方策と探索方策が同じ

    代表的なアルゴリズム：REINFORCE、SARSA、Actor-Criticの大半

  • 方策オフ

    学習する方策と探索方策が別（でも良い）

    代表的なアルゴリズム：Q学習、DQN系

• この分類が生む違い（Exploration-Exploitation Trade-off）

  強化学習はエージェントが行動して集めたデータで学習するものです。価値を最⼤化するような貪欲（greedy）な最適⽅策を最終的に得たいわけですが、これを探索方策に使うと、学習中にその時点で最善の行動ばかり選ぶようになるため、新しい⾏動を試さなくなり、学習に偏りが生じてしまいます。

  この話はよく「多腕バンディット問題」が例に使われます。何台もあるスロットから1台選んで報酬を受け取ることを繰り返すとします。この報酬を最大化するには、当たりやすいスロットを選び続けるのが良さそうですが、最初の方にそこそこ良いスロットを見つけたからといって、そればかり選んでいては、より当たりやすいスロットを選ぶ機会を失います。一方で完全にランダムでも報酬は最大化できないでしょう。このような板挟みを「活用と探索のトレードオフ（Exploration-Exploitation Trade-off）」と言います。

  このような問題を解決するために、探索方策として「⾏動にノイズ（ランダム性）を載せる」というものを使うことが多いです。

  さて、探索方策でデータを集めて学習すると、方策オフであるQ学習は greedy な方策が使われる想定で価値関数を学習しますが、方策オンであるSARSAではランダム性のある方策がそのまま使われる想定で価値関数を学習をするのです。

  例えば、以下の図のような崖の近くを歩いてゴールに行く問題を考えます（cliff walk）。
  左下からスタートして、右下の黄色に行きます。黒いマスが崖で、白いところをエージェント（左下にいる小さい四角）が動きます。

  
  https://qiita.com/abmushi/items/83a639506fcbc4050ce8

  最短でゴールに行くほど報酬は高いですが、崖から落ちるとペナルティなので、崖から落ちたくはありません。ここで行動にノイズを載せるということは、エージェントが行動の際に判断した方向でない向きにランダムに移動させられるということです。

  この問題について SARSA と Q学習の学習結果の違いがわかりやすい図があったので引用します。
  SARSA
  
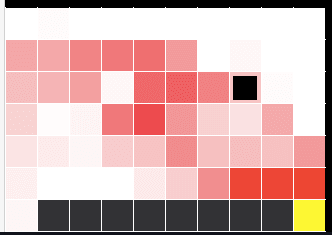
  https://qiita.com/abmushi/items/83a639506fcbc4050ce8
  Q学習
  
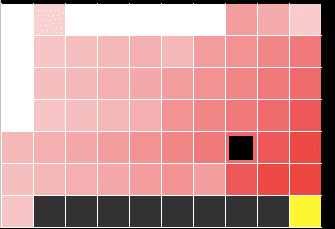
  https://qiita.com/abmushi/items/83a639506fcbc4050ce8

  赤が濃いほど価値を高く見積もっています、つまり赤いところを歩くのが良いと考えられています。この問題で最適な⽅策は崖沿いを歩くことですが、方策オンであるSARSAで学習した方策では、一度上まで行くのが良いとされています。崖から落ちることを恐れている証拠です。
  学習を終えて実際に使うときはノイズは載せずに greedy な方策で使えば良い（つまり赤が濃いところを辿れば良い）ので、理にかなった価値の見積もりには見えませんが、学習中に行動を集めている時は、そんなつもりはなくても下に動かされてしまう可能性があるので、「最初はできるだけ崖から離れておいた方がいい」と考えるのは納得できます。

  ⼀⽅で、⽅策オフでは学習時の⽅策に関係なく、学習済みエージェントが⾏動する際は貪欲な⽅策で⾏動する前提で学習するため、学習した価値の分布では崖沿いほど価値が⾼くなります。

  ここまでは方策オンと方策オフの違いの紹介でした。SARSAは方策オンでQ学習は方策オフであるとさらっと書きましたが、それを確認してみます。

  SARSAの更新式は

  $$Q(s, a) \leftarrow Q(s, a)+\alpha\left\{r+\gamma Q\left(s^{\prime}, a^{\prime}\right)-Q(s, a)\right\}$$

  であり、教師信号の作成に使われる行動 $a'$ は探索中に実際に取った行動、つまり探索方策によるものです。

  Q学習の更新式は

  $$Q(s, a) \leftarrow Q(s, a)+\alpha\left\{r+\gamma \max _{a_{next}} Q\left(s^{\prime}, a_{next}\right)-Q(s, a)\right\}$$

  であり、SARSAでの表記に合わせて教師信号の作成に使われる行動を $a^*$ とするなら、$a^* = \argmax_{a_{next}} Q(s', a_{next})$ となります。これは $\max$ による処理が greedy な方策であることを意味しているので、greedy な方策であって探索方策ではありません。

モデルベース・モデルフリー

• 各分類の紹介

  • モデルベース

    エージェントが環境のモデル（状態遷移関数と報酬関数）を学習・使用する

    代表的なアルゴリズム：動的計画法（DP: Dynamic Programming）

  • モデルフリー

    エージェントが環境のモデルを明示的に使用せず、経験から学習する

    代表的なアルゴリズム：Q学習、SARSA、DQN、REINFORCE、Actor-Critic

まず「モデル」という言葉が機械学習でよく使われる「予測モデル」ではないという点で紛らわしいので注意です。次に、モデルベースの説明として、「エージェントが環境のモデルを既知の時」とする説明もよく見かけますが、上記の説明もよくあります。既知である時は学習する場合の特殊なケース（学習済みと考えれば良い）なので、上記の説明の方が一般性が高くて良いかと思います。

• モデルベース

  • 動的計画法

    環境のモデルが既知である時に、反復的にベルマン方程式を解いて最適な方策を得る

    サブセットとして、価値反復法、方策反復法がある

• モデルフリー

  ここまでに出てきたアルゴリズムは全てモデルフリーなのでここでは省略します。

Actor-Critic 系

ここで Actor-Critic を別にしたのは、単に自分がよく勉強した（自分が考案したアルゴリズムが Actor-Critic をベースにした）のでより細かく分割できるからです。これまでの分類と並列とは言えません。Actor-Critic 全体の位置付けを確認しておくと、

• 方策ベース（Criticは価値ベース）
• Criticの価値関数の更新はTD法
• 基本的に方策オン
• モデルフリー

となります。

自分の修士論文より引用

具体的に見ていきます。

• A3C：Asynchronous Advantage Actor-Critic

  特徴は以下の２つ

  • 複数のエージェントがコピーされた環境で学習し、中央のネットワークのパラメータを非同期的に更新する
  • advantage を用いて学習する

  各エージェントのネットワークの重みは、定期的に中央のネットワークの重みと同期される。これにより、学習を高速化・安定化させられる。
  方策オンである actor-critic は experience-replay が使えないため、エージェントを並列化するというアプローチで、経験間の相関を低減させている、と言える。

• A2C：Advantage Actor-Critic

  特徴は以下の２つ

  • 複数のエージェントが中央のネットワークの方策のもと学習し、一定タイミングでそれらの勾配情報を集約して中央のモデルを更新する
  • advantage を用いて学習する

  つまり、A3Cの同期的なもの。

  勾配計算をするのが中央だけで良いため、計算リソースが A3C に⽐べて少なくて済む。

• TRPO：Trust Region Policy Optimization

  ⽅策の更新時、更新後の⽅策と更新前の⽅策の KL ダイバージェンスを⼀定の範囲（trust region）に収めるという制約を設けたアルゴリズム。
  （KLダイバージェンスとは、分布間の類似度のようなもの）

  ⽅策勾配定理によって⽅策関数を更新した際に、パラメータを⼤きく更新しすぎると⽅策が劣化し、さらにその場合改善が難しくなるという課題に対処するためのもの。

• PPO：Proximal Policy Optimization

  方策の更新時、更新後の⽅策と更新前の⽅策の⽐率を⼀定の範囲に収めるという制約を設けたアルゴリズム。

  TRPO がこの範囲を KL ダイバージェンスを使って決めていたのに対し、PPO では単純にハイパーパラメータで指定した値で範囲を指定する。
  これにより、TRPOよりも計算コストを抑えられる。

• DPG：Deterministic Policy Gradient

  Actor-Critic を行動が連続かつ決定論的な⽅策の学習のためのアルゴリズム。

  連続値の行動を出すとき、一般に方策ベースのアルゴリズムは、確率分布を出すと書いたが、これを決定論的に使う場合は、例えば正規分布ならその平均を分布の代表値として使うことで決定論的な出力とする。
  これに対し、DPGは最初から直接行動の連続値を出力する。

  この時、方策の勾配は Q関数の勾配を使って求められる。また、状態空間についてのみ期待値をとれば良いので、特に状態空間が大きい問題において、勾配を少ない計算量で求められる。

  DPGの特徴として、方策オフである。方策の更新にQ値を使うので、Critic もQ値を推測すれば良い。この時、古い方策で集められた状態であっても、新しい方策で行動を選択し直し、その状態行動対についてQ値を計算し直せば良いからである。

• DDPG：Deep Deterministic Policy Gradient

  DNN を DPG に適⽤したアルゴリズム。

  経験再⽣やソフトな target network といったテクニックが使われる。

  DDPG は決定論的な⽅策に基づいた⾏動を取るため。学習時に探索的⾏動をするためには別途ノイズを乗せる必要がある。

学習テクニック

• $\epsilon$-greedy

  • 概要

    ある確率 $\epsilon$ で行動をランダムに選択する、というもの

    具体的には、$\epsilon$ を決め、行動選択の際同時に 0~1 の乱数を生成し、その値が $\epsilon$ を下回ればランダムに行動する、という方法

    一般的には学習が進むにつれて、$\epsilon$ を小さくしていく

  • どのような課題に対処するための手法か

    活用と探索のトレードオフ

  • これを使えるアルゴリズム

    価値ベース

    $\epsilon$-greedy は「行動選択」と書いてある通り、これは価値ベースのアルゴリズムで使うもので、探索の段階で使う

• Target network

  • 概要

    実際に⾏動し学習を⾏うネットワークとは別のネットワークに教師信号を作らせるというもの

    例えば、「価値関数の更新」で例に挙げた DQN では target network を使っている

    この式では、target network が１つ前のイテレーションのものとされているが、一般には一定期間ごとに学習をするネットワーク（main network）と target network を同期して target network の重みを更新する

    同期の方法として、一定期間ごとに同期するハードなもの、毎回一定の更新率 $\tau \ (0<\tau \leq 1)$ で更新するソフトなものとがある

  • どのような課題に対処するための手法か

    main network と同じネットワークの評価から教師信号を作ると、学習のたびに教師信号が変わることになり、学習が安定しない、という課題

  • これを使えるアルゴリズム

    方策オフ

    方策オンだと、すぐに方策を更新するため

  • 例

    Double DQN, DQN での target network の違いを紹介する

    これらはどちらも target netwrok の DQN に行動を評価させて教師信号とするわけだが、その行動の取り方に違いがある

    • DQN：target network を使って選択する
    • Double DQN：main network を使って選択する

• 経験再生（experience replay）

  • 概要

    エージェントが⾏動の結果得られた経験（主に状態、⾏動、報酬、次の状態といった情報）をリプレイバッファ（replay buffer）と呼ばれるメモリに保存しておき、後にそれらの経験をランダムに取り出して学習に使うというもの

  • どのような課題に対処するための手法か

    RL は一般に学習に使われる経験同士の相関が強く、そのため学習が不安定になる、という課題

  • これを使えるアルゴリズム

    方策オフ

    リプレイバッファに溜まった経験は、その時の探索方策によって得られたものである。方策オンでは、別の方策で得られた経験を使って学習することはできない

付録

価値

本文中で、価値とは「『これから先得られる報酬の累積』の期待値」であると書きました。

まずは報酬の累積を考えます。というのも、普通に足し上げるのではありません。⼀般に未来の報酬は不確実性が⾼く、あまり当てにすべきではないので、未来の報酬ほど割り引いて現在の価値に直し、報酬の累積を考えます。これを割引累積報酬と言います。

$$\begin{aligned}G_t & =r_{t+1}+\gamma r_{t+2}+\gamma^2 r_{t+3}+\cdots \\& =\sum_{k=0} \gamma^k r_{t+k+1}\end{aligned}$$

ここで $\gamma$ は割引率で、 $0 \le \gamma \le 1$ です。

ではこの期待値を考えましょう。期待値は方策に依存する（その時点以降どれぐらい報酬が得られるかは報酬による）ので、$\mathbb E _\pi$ として以下の式で表されます。

$$\begin{aligned}& \mathbb{E}_\pi\left[\sum_{k=0} \gamma^k r_{t+k+1} \mid s_t=s\right] \\& =\mathbb{E}_\pi\left[r_{t+1}+\gamma \sum_{k=0} \gamma^k r_{t+k+2} \mid s_t=s\right] \\& \end{aligned}$$

もうちょっと変形すれば、漸化式っぽく表せそうです。期待値を外すことを考えます。

簡単のため、状態・⾏動ともに離散空間で考えることにします。

時刻 $t$ で状態 $s$ であるとします。ここで方策 $\pi (s, a)$ に従って行動を選択します。一般に $\pi$ は確率を返すものです（つまり次時点の各行動 $a, a', a''$ に確率が割り振られます）。

その確率に従って行動 $a$ が選択されると、状態遷移関数 $p_T$ によって各状態に遷移する確率が計算されます。$p_T(s'|s, a)$ は状態 $s$ で行動 $a$ をとった時に状態 $s'$ に遷移する条件付き確率を表します。

次の状態に遷移したところで時刻は 1 ステップ進み、報酬が払われます。

以上を図に示すと、以下のようになります。

自分の修士論文より引用

$a$ を固定して $s'$ について各分岐の確率をかけて和をとり、 その後 $a$ について各分岐の確率をかけて和を取ると考えると

$$\mathbb{E}_\pi\left[\sum_{k=0} \gamma^k r_{t+k+1} \mid s_t=s\right] = \sum_a \pi(s, a) \sum_{s^{\prime}} p_T\left(s^{\prime} \mid s, a\right)\left\{r_{s, a, s^{\prime}}+\gamma \mathbb{E}_\pi\left[\sum_{k=0} \gamma^k r_{t+k+2} \mid s_t=s^{\prime}\right]\right\}$$

これをベルマン方程式（Belleman equation）と呼びます。

さて、ここで以下のように状態価値と行動価値を定義します。

• 状態価値 $V$

  状態 $s$ の時点からみた割引累積報酬の期待値

  これも方策に依存するので、以下のように書けます。

  $$V^\pi(s) = \mathbb{E}_\pi\left[\sum_{k=0} \gamma^k r_{t+k+1} \mid s_t=s\right]$$

• 行動価値 $Q$

  行動 $a$ の時点からみた割引累積報酬の期待値

  行動も引数になります。

  $$Q^\pi(s,a) = \mathbb{E}_\pi\left[\sum_{k=0} \gamma^k r_{t+k+1} \mid s_t=s, a_t = a\right]$$

これより、ベルマン方程式は次のように書けます。

$$V^\pi(s)=\sum_a \pi(s, a) \sum_{s^{\prime}} p_T\left(s^{\prime} \mid s, a\right)\left\{r_{s, a, s^{\prime}}+\gamma V^\pi\left(s^{\prime}\right)\right\}$$

$$Q^\pi(s, a)= \sum_{s^{\prime}} p_T\left(s^{\prime} \mid s, a\right)\left\{r_{s, a, s^{\prime}}+\gamma V^\pi\left(s^{\prime}\right)\right\}$$

改めて、状態価値、行動価値を先ほどの図に対応させると、以下のようになります。

自分の修士論文より引用

価値関数の更新

では、価値関数の更新式の意味を確認してみます。

例えば、Q学習の更新式は以下の通りでした。

$$Q(s, a) \leftarrow Q(s, a)+\alpha\left\{r+\gamma \max _{a_{next}} Q\left(s^{\prime}, a_{next}\right)-Q(s, a)\right\}$$

以下のように書き換えてみます。

$$Q(s, a) \leftarrow (1-\alpha) Q(s, a)+\alpha\left\{r+\gamma \max _{a_{next}} Q\left(s^{\prime}, a_{next}\right)\right\}$$

この式の意味するところは、今の行動価値に、次のステップの行動価値で表した現在の価値を学習率 $\alpha$ の割合でブレンドして、今の行動価値にしよう、というものです。こういうソフトな更新というのは強化学習に限らずよくあるものです。

そこで、この学習率を除いて考えてみます。全く学習しない場合、つまり $\alpha = 0$ の時、$Q$ は変化なしであることを確認してください。では、完全に更新する場合はというと、$\alpha = 1$ より、以下の通りになります。

$$Q(s, a) \leftarrow r+\gamma \max _{a_{next}} Q\left(s^{\prime}, a_{next}\right) \tag{*}$$

なぜこの式が成り立つのか考えます。まずは、行動と状態遷移が決定論的であるとしてみます。つまり、「ある状態ならこう行動する、ある状態でこの行動ならこの状態に遷移する」と決まっている場合です。以下の図でいうと、状態 $s$ が与えられると、行動 $a$ を取って、状態 $s'$ に必ず移行する場合です。

自分の修士論文より引用
この時、Q値のベルマン方程式は、

$$Q(s, a) ＝ r+ \gamma V\left(s^{\prime}\right)$$

となりますが、$s'$ でとる行動も決まっているので、これを $a^*$ とすると、

$$Q(s, a) ＝ r+ \gamma Q\left(s^{\prime}, a^*\right)$$

となります。$Q(s,a)$ と $r+ \gamma Q(s', a^*)$ は等しいのですから、$Q$ を $r+ \gamma Q(s', a^*)$ で置き換えても良さそうです。式 (*) に少し近づいてきました。

次にこれを一般の場合、つまり行動選択も状態遷移も確率的である場合に戻してみます。
まずは $\max$ の意味を考えてみます。方策を確率的に直すと、状態 $s'$ でとる行動 $a^*$ がわからなくなります。そこで、エージェントの方策も考えてやる必要があります。以下の話は、「方策オン・オフ」のセクションで書きましたが、ここでも再掲します。例えばQ学習では、状態 $s'$ で、$Q(s', a_{next})$ を最大化する $a_{next}$ を選択するとしています。上の式を踏まえてあえて２つの式で書くと、

$$Q(s,a) \leftarrow r + \gamma Q(s',a^*) \\ a^* = \argmax_{a_{next}} Q(s',a_{next})$$

となります。２つ目の式を見るとわかりやすいですが、つまりは greedy な方策をここに反映しているわけです。「方策オン・オフ」のセクションで、「Q学習は greedy な方策を前提として学習する」と書いたのはこのことです。greedy な方策で取った行動で得られる次のQ値を使って、現在のQ値を更新しています。「方策オン・オフ」のセクションでは SARSA の更新式についても書いていますので、ご確認ください。

一応先ほどの２つの式を合わせれば、Q学習の更新式はでますが、これを勉強している当時の自分には、次のような疑問が残りました。それは、「$r + \gamma Q(s',a^*)$ は１つの行動の結果なのに価値として使っていいの？」というものです。方策も状態遷移も確率的な話に戻すということは、Belleman 方程式の期待値の計算を真っ向から相手にすることになりそうだと思っていました。であれば、１つの結果を使って（上の図で言うと、$s,a,s'$ を繋いだパスで、分岐のツリー全体の一部でしかない）、勝手に期待値を外しているのはいいのか？となったわけです。
結論から言うと、これはそういう更新の手法なのです。その手法というのは、本文中のコラムで触れた「ブートストラップ」です。
上の自分の話で間違っているのは、別に $Q(s,a) = r + \gamma Q(s',a^*)$ である必要はないということです。等式が成り立つものでしか更新してはいけないということはありません。そもそも、普通は Belleman 方程式は計算できるものではありません。全ての分岐を尽くすのが非現実的だと思っていただければいいかと思います。
そんなわけでブートストラップを使う必要があるわけです。ブートストラップは何度も繰り返せば、最適なQ値に収束することがわかっているそうです。
というわけで晴れて期待値の心配もなくなり、式 (*) の意味が確認できました。

方策勾配

方策ベースのアルゴリズムを実装するだけなら、方策勾配は前提として始まるので、方策勾配の式を知っていれば、PPOとかTRPOとかの話もわかります。
が、一応何かの参考になればということで、1年前ぐらいに書いた方策勾配の導出の手書きを載せます。世にある導出がわかりづらかったので、自分なりに咀嚼しながら書いたものです。あんまり確認せず載せるので、間違っていたらすみません（教えてください）。
改めて、方策勾配の式を確認すると、以下のようになります。

$$\nabla_\theta J(\theta)=\mathbb{E}_{\pi_\theta}\left[\nabla_\theta \log \pi_\theta(a \mid s) Q^{\pi_\theta}(s, a)\right]$$

ここで $J$ は初期状態からみた状態価値です。ということで？ $V$ の $\theta$ による偏微分から考えています。