XGBoostで株価LogReturn予測――“カテゴリ変数”で予測AIはここまで変わる
本記事は前回の「株価データ分布の可視化とカテゴリ分岐設計」(記事はこちら)の続編です。
前回のデータ分析で設計したカテゴリ分岐をもとに、今回は実際にAIで株価LogReturn予測を行い、「カテゴリ変数の有無」で精度や予測分布がどう変わるかを徹底検証しました。
検証の目的
「翌営業日の終値LogReturn(=前日比の変動率)」をXGBoostで予測するタスクにおいて、
-
カテゴリ変数(例:価格帯やグループ)を追加すると予測精度やモデルの挙動がどのように変化するのか?
を実験・分析します。
実験概要
-
モデル:XGBoost
-
予測対象:翌営業日の終値LogReturn(=終値の前日比変動率、単位は%ではなくLog値)
-
特徴量パターン:
- V4:カテゴリ変数なし
- V5:カテゴリ変数あり
-
評価指標:MAE(平均絶対誤差)、RMSE(二乗平均平方根誤差)、相関係数(予測vs実測) ほか
【図表・写真挿入位置とキャプション一覧】
-
図1. mediumグループ・カテゴリ変数なし(V4)の予測結果散布図
(実測LogReturnと予測値の関係。点が直線から大きくバラつく=予測が外れている例が多い) -
図2. mediumグループ・カテゴリ変数なし(V4)の予測誤差ヒストグラム
(誤差0から右方向にピークがずれている=過小評価バイアスの傾向を可視化) -
図3. mediumグループ・カテゴリ変数あり(V5)の予測結果散布図
(実測LogReturnと予測値が直線付近に集まり、モデルが“動きをしっかり当てている”様子) -
図4. mediumグループ・カテゴリ変数あり(V5)の予測誤差ヒストグラム
(誤差0への集中が強化。外れ値の頻度も激減し、“外さないAI”に進化した様子) -
図5. smallグループ・カテゴリ変数なし(V4)の予測結果散布図
(small銘柄でも、カテゴリ変数なしでは点が縦に散らばりやすい傾向) -
図6. smallグループ・カテゴリ変数なし(V4)の予測誤差ヒストグラム
(0以外にも複数ピークや裾野が見える=外れ値・予測ブレが多い) -
図7. smallグループ・カテゴリ変数あり(V5)の予測結果散布図
(カテゴリ変数追加により、点が直線付近に密集し“正解に追従するAI”の特性が現れる) -
図8. smallグループ・カテゴリ変数あり(V5)の予測誤差ヒストグラム
(0付近への寄り付き・密度がさらに強化。誤差の大外れが大幅に減少した) -
表1. MAE・RMSE等の指標比較表
(small/medium/large各グループのモデルごとの主要指標を一括比較。カテゴリ変数導入で精度・安定性が飛躍的に向上していることが数値で見て取れる)
補足注釈
各図・表は、カテゴリ変数導入の有無によるAIの予測精度・分布変化を視覚的・定量的に比較しています。
図1~4はmediumグループ、図5~8はsmallグループの挙動を示し、表1では全体傾向を定量的にまとめています。
検証結果(グループごと)
表1. MAE・RMSE等 指標比較
| モデル | グループ | MAE | RMSE | R2 | MAPE |
|---|---|---|---|---|---|
| chartyx_v4 | small | 0.138 | 0.216 | -25.76 | 1752.55 |
| chartyx_v4 | medium | 0.366 | 0.436 | -108.78 | 5513.39 |
| chartyx_v4 | large | 0.274 | 0.363 | -74.81 | 4498.73 |
| chartyx_v5 | small | 0.053 | 0.073 | -2.02 | 854.59 |
| chartyx_v5 | medium | 0.081 | 0.106 | -5.42 | 1243.86 |
| chartyx_v5 | large | 0.149 | 0.254 | -36.11 | 2321.01 |
※表内のV4=カテゴリ変数なし、V5=カテゴリ変数あり
可視化で見る精度の違い
mediumグループの「誤差ヒストグラム」を例に、カテゴリ変数あり/なしでどう分布が変わったかを比較します。
※他グループも同様の傾向が見られました。
medium/GroupAvg_medium の例(LogReturn予測)
カテゴリ変数なし(V4)の予測分布

図1. 「カテゴリ変数なし」モデルの予測結果散布図(横軸: 実測LogReturn、縦軸: 予測値、赤線: 完全一致)

図2. 「カテゴリ変数なし」モデルの予測誤差ヒストグラム(横軸: 誤差, 縦軸: 頻度)
カテゴリ変数あり(V5)の予測分布

図3. 「カテゴリ変数あり」モデルの予測結果散布図

図4. 「カテゴリ変数あり」モデルの予測誤差ヒストグラム
結果まとめ・図の読み解き
-
Predicted vs Actual散布図(図1,3)では、点がy=x(赤線)に近いほど予測精度が高いことを示します。
カテゴリ変数なし(V4)では点がバラつきますが、あり(V5)では直線付近に密集し、相関係数も明確に向上しています。 - 誤差ヒストグラム(図2,4)では、「誤差0」(=予測が実測と一致)に山が集中し、裾野(大外れ)が減少。“外さない予測”が増えたことを示します。
smallグループでも同様の傾向が見られます。
実際の誤差ヒストグラムでは、カテゴリ変数を導入することで中心(0付近)への寄り付きがさらに強くなり、大外れのケースも大きく減少しました。
分散が一時的に増えたように見える場面もありますが、これは**“予測誤差が0に集中する”ことで中心密度が増したため**です。
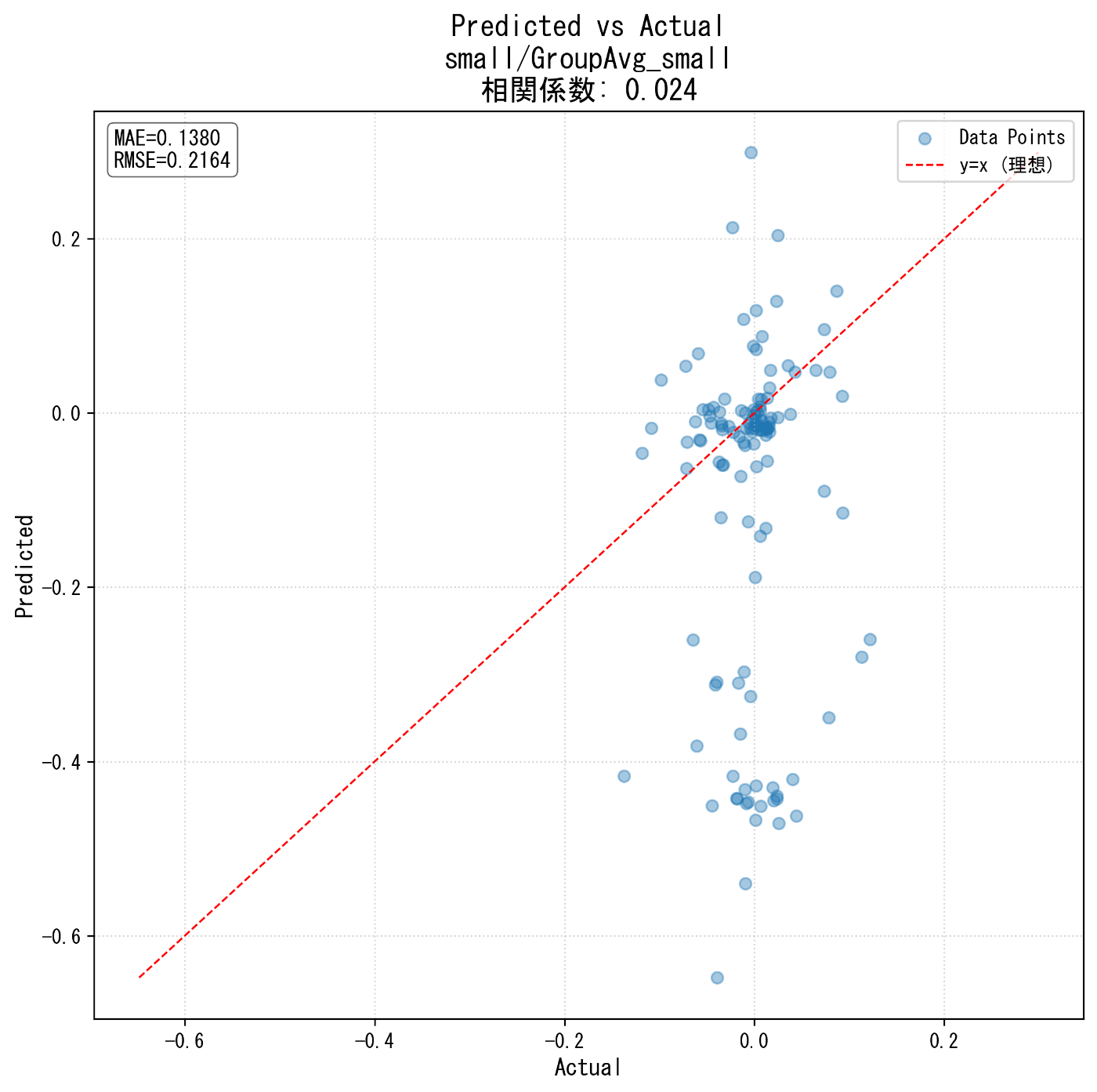
図5. smallグループ:カテゴリ変数なしの予測結果散布図

図6 smallグループ:カテゴリ変数なしの予測誤差ヒストグラム

図7 smallグループ:カテゴリ変数ありの予測結果散布図

図8 smallグループ:カテゴリ変数ありの予測誤差ヒストグラム
なぜカテゴリ変数が効くのか?
- 株価データには**「異質なグループ」**(価格帯/業種/流動性など)が混在しており、そのまま学習させると「全体平均」に引っ張られがち
- カテゴリ変数を追加することで、AIは「今どのグループのデータか」を認識し、それぞれの特徴に合わせた予測が可能に
- 結果として「外れ値の暴走」や「過小評価」が抑制され、全体の精度・安定性が大幅向上!
まとめ・今後の展望
- カテゴリ変数の追加は、株価予測AIの“精度と頑健性”を飛躍的に高める強力な工夫
- 今後は、SHAP値による特徴量重要度の可視化や、「どのカテゴリが最も効いているか?」の深堀り分析も予定
次回もお楽しみに!
前回記事(こちら)で紹介した「分布分析・カテゴリ設計」と合わせてご覧いただくと、より理解が深まります。
さらに理解を深めたい方へ:補足Tips
- Predicted vs Actual散布図では「点がy=x直線(赤線)に集まる=どんな変動幅でも実測値をしっかり当てている」ことを意味します。相関係数はこの“一致度”の良さを数値で表す重要指標です。
- 誤差ヒストグラムは「0に山が集まる」ほど、実用的に“外さないAI”になった証拠。分散や尖度も参考指標ですが、中心密度の高さをまず注目しましょう。
Discussion