円と矩形の角の弾性衝突をTypeScriptで実装する
はじめに
年の瀬が迫ってくると衝突判定を実装したくなりますね!
矩形同士、円同士、矩形と円など色々ありますが、本記事では円と矩形の角の弾性衝突を実装します
弾性衝突とは
ざっくり言うと、運動エネルギーが失われない(保存される)衝突のことです
ボールを自由落下させて延々とバウンドし続けるならボールと地面は弾性衝突しているし、だんだんとボールのバウンドする高さが縮まっているなら非弾性衝突です
円と矩形の角の弾性衝突
矩形の辺との衝突は結局ただ直線との衝突ですが、矩形の角との弾性衝突は少し考える必要があります
ちょっと検索してみてもプログラミングという文脈で情報が多くはないので書いていきます
こういうことです↓

デモ
ボールを5つ初期座標と初期速度ランダムで設置しているのでたまに角に当たるのが見れると思います
ボール同士の弾性衝突(以下「衝突」といいます)は実装してません
灰色の壁とブラウザの端とだけ衝突します
src/constants.tsに壁の座標と大きさの設定があるので自由にいじれます
ボールの衝突のロジックは全部 src/moveCircle.ts に書いてあります
壁の辺との衝突の解説は省略します
実装/解説
React/TypeScriptで実装しますが他のライブラリを使わないので基本TypeScriptです
どの角と衝突したかを判定
// 移動前の座標
const pos = { x: number, y: number };
// 速度
const velocity = { x: number, y: number };
// 移動後の座標
const newPos = { x: pos.x + velocity.x, y: pos.y + velocity.y };
// 障害物
const rect = {
x: number, y: number, // 矩形の左上の点
width: number, height: number,
};
// ボールが障害物に対して上下左右どっち側にあるか
const leftSide = newPos.x <= rect.x;
const rightSide = rect.x + rect.width <= newPos.x;
const topSide = newPos.y <= rect.y;
const bottomSide = rect.y + rect.height <= newPos.y;
// 衝突する可能性のある角の点を判定
const cornerPoint = { x: -1, y: -1 };
if (leftSide) {
if (topSide) {
cornerPoint.x = rect.x;
cornerPoint.y = rect.y;
} else if (bottomSide) {
cornerPoint.x = rect.x;
cornerPoint.y = rect.y + rect.height;
}
} else if (rightSide) {
if (topSide) {
cornerPoint.x = rect.x + rect.width;
cornerPoint.y = rect.y;
} else if (bottomSide) {
cornerPoint.x = rect.x + rect.width;
cornerPoint.y = rect.y + rect.height;
}
}
const distance = (x1, y1, x2, y2) => { /* 2点間の距離を計算 */ };
if (distance(newPos.x, newPos.y, cornerPoint.x, cornerPoint.y) <= CIRCLE_RADIUS) {
// 角との衝突による跳ね返りを計算(この後説明します)
}
これで「衝突した時のボールの座標(と速度)」「衝突した角の座標」がわかったので跳ね返りを計算できます
どうやって跳ね返りを計算するか
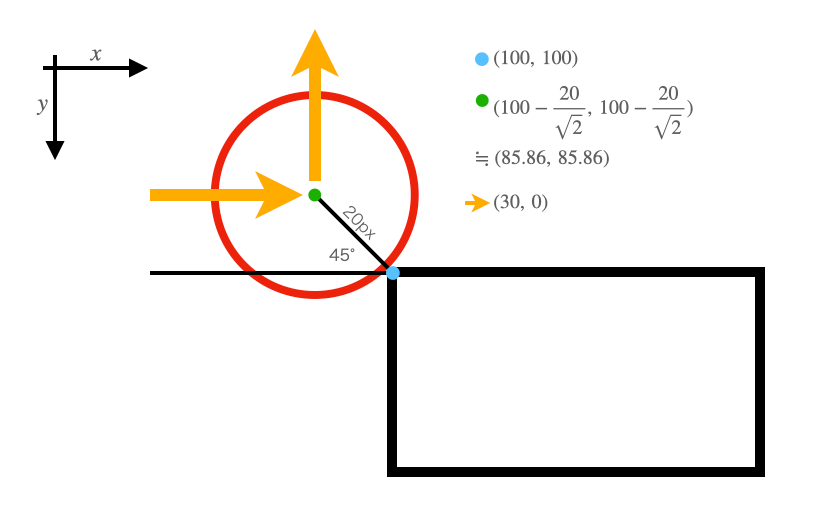
図解します
さっき出した絵ですが少し書き加えました

オレンジ色の矢印が速度ベクトルです
| 衝突した角を原点と考えて、衝突した角とボールの中心を結ぶ線(水色)で速度ベクトルを線対称変換 | 変換後の速度ベクトルの向きを逆にする |
|---|---|
 |
 |
以上のようにして衝突後の速度ベクトルが計算できます
衝突後の速度ベクトルを計算
ではコードで説明していきます
if (distance(newPos.x, newPos.y, cornerPoint.x, cornerPoint.y) <= CIRCLE_RADIUS) {
// 線対称変換
const reflectedVector = reflectVectorAcrossLine(
// 速度ベクトル
velocity,
// 衝突した角を原点としたボールの中心へのベクトル
{ x: newPos.x - cornerPoint.x, y: newPos.y - cornerPoint.y },
);
// 最後に向きを逆にする
newVelocity.x = reflectedVector.x * -1;
newVelocity.y = reflectedVector.y * -1;
}
最後にreflectVectorAcrossLineのコードです
interface Vector {
x: number;
y: number;
}
// ベクトルのノルム
const norm = (vector: Vector) => Math.sqrt(vector.x * vector.x + vector.y * vector.y);
// 単位ベクトル化
const unitVectorize = (vector: Vector) => {
const vectorNorm = norm(vector);
return { x: vector.x / vectorNorm, y: vector.y / vectorNorm };
};
// 線対称変換
export const reflectVectorAcrossLine = (vector: Vector, lineVector: Vector) => {
// (1) 速度ベクトルと線ベクトルを単位ベクトル化
const unitVector = unitVectorize(vector);
const unitLineVector = unitVectorize(lineVector);
// (2) 速度単位ベクトルと線単位ベクトルの内積を計算
const dotProduct = unitVector.x * unitLineVector.x + unitVector.y * unitLineVector.y;
// (3) 速度ベクトルのノルム(長さ)を計算
const vectorNorm = norm(vector);
// (4) 線対称変換
return {
x: (2 * dotProduct * unitLineVector.x - unitVector.x) * vectorNorm,
y: (2 * dotProduct * unitLineVector.y - unitVector.y) * vectorNorm,
};
};
(1) 速度ベクトルと線ベクトルを単位ベクトル化
黒いのが単位ベクトルです
今はWebブラウザ上での計算をしているので単位はpx(ピクセル)
つまり単位ベクトルは長さ1pxの方向(角度)が同じベクトルということになります

計算で使用するときに単位ベクトルだと何かと都合がいいので単位ベクトル化します
ベクトルの長さをピタゴラスの定理を用いて計算、ベクトルを割り算すると単位ベクトル化できます
後でも出てきますがこの長さをベクトルにおいてはノルムと言ったりします
const vector = { x: 4, y: 3 };
const norm = Math.sqrt(vector.x * vector.x + vector.y * vector.y); //=> 5
const unitVector = { x: vector.x / norm, y: vector.y / norm };
//=> { x: 4/5, y: 3/5 }
(2) 速度単位ベクトルと線単位ベクトルの内積を計算
線対称変換で使うため内積を計算します
ベクトル
コードにするとこうです
const vectorA = { x: 3, y: 2 };
const vectorB = { x: 4, y: -2 };
const vectorC = { x: -4, y: 6 };
// A・B
const dotProductAB = vectorA.x * vectorB.x + vectorA.y * vectorB.y;
//=> 3*4 + 2*(-2) = 8
// A・C
const dotProductAC = vectorA.x * vectorC.x + vectorA.y * vectorC.y;
//=> 3*(-4) + 2*6 = 0 (AとCは垂直)
内積が0の場合垂直であることがわかります
(3) 速度ベクトルのノルム(長さ)を計算
(1)で説明したままです
この後の計算に使うので速度ベクトルのノルムを求めておきます
(4) 線対称変換
お待ちかねの線対称変換です
が... 公式をそのまま活用するので理論の解説は本記事では省略します
公式はこちらです
線対称変換前の単位ベクトルを
線対称変換後の単位ベクトル
単位ベクトル化する前に直すためにノルムをかけて完了
これを見てもよくわからないのでコードにします
const v // 変換対象の単位ベクトル
const l // 線対称変換で使う単位線ベクトル
const dotProduct // 単位ベクトル同士の内積
const vectorNorm // 変換対象のベクトルのノルム(長さ)
const v' = {
x: (2 * dotProduct * l.x - v.x) * vectorNorm,
y: (2 * dotProduct * l.y - v.y) * vectorNorm,
};
// 数式との対応をわかりやすくするために v' と表記してますがTypeScriptだと使えない変数名です
これで線対称変換は完了です
検証実験
デモではそれっぽく見えるけど実際計算過程に多少のミスがあって目視ではわからないくらいのずれがある可能性もあるので検証実験をしておきます
直角に跳ね返るケース
実験結果


衝突した瞬間(2)と跳ね返った後(3)の
(3)の
真っ直ぐ跳ね返るケース

実験結果

(1) 角に衝突する前
(2) 角に衝突した瞬間
(3) 角に衝突した後
になります
真っ直ぐ跳ね返ることを期待しているので、(1)と(3)が同じ座標だと嬉しいです
(1)と(3)で誤差はあれど大体同じところに跳ね返ったのがわかります
おわりに
ということで円と矩形の角の弾性衝突の実装がうまくいったのではないでしょうか!
今回は固定された矩形の角との弾性衝突について考えましたが、まだまだかなりできることが多いと感じました
本記事ではすり抜けを妥協して考慮しませんでしたが、しっかり考えようとするとなかなか複雑になります
他には矩形も動く場合、質量を考慮して運動エネルギーの総量が変わらないように弾性衝突させようとすると考えることが増えます
さらには矩形が回転する場合、力のモーメントなんかも考える必要があります
これを3Dにすると計算量が莫大に膨れ上がりそうです
壁の数が増えたり動いている物体同士で衝突させると計算量が増えすぎてまともに動作しなくるまであるので計算の効率化なんてこともできそうです
なかなか奥が深いですね!
ところで、なぜCanvasを使わないのだろうか?と疑問に思う方もいらっしゃると思います
深い理由はなく単にこだわりです
面白いアニメーションをコンソールで確認したときにDOMで表現されていたらアガりますよね
情報をセマンティックに伝えるために設計されたHTMLで変なことしてる感がものすごく好きです
なぜ本記事を書こうかと思ったかというと
この後いつか「マルチディスプレイ/マルチウィンドウを1つの平面としてボールをバウンドさせる」という記事を書こうと思ってるのですが、その際に考慮する必要があるためです
例えばこのようなディスプレイ配置の場合結構な数の角ができます

弊宅のディスプレイ環境です、必要以上に繋げています
この繋がった平面を1つのフィールドとして考えると色々面白いことができそうだなと思いブラウザ内でやる方法を思いたのでそのうちやっていきます
それでは次回があれば、またいつか
Discussion