[survey]Learning a logistic model from aggregated data

メモ代わりなので悪しからず。(言い訳)

論文情報

タイトル: Learning a logistic model from aggregated data
著者: Alexandre Gilotte et al (Criteo)
出自: AdKDD 2021

---

どのような研究か(要約)

プライバシー保護の観点から従来学習に利用していたデータを取得し続けることは難しくなることが予想されており、生データではなくAggregated Data(生データに対し各種統計処理がかけられたデータ、集約データ)からモデルを学習する必要がある。しかし従来の教師あり学習を集約データに直接適応することは難しいため、代替する方法を検討する必要がある。
本研究では、従来の教師あり学習ではなくMRFを用いた確率モデルを適用することで集約データから直接学習する手法を提案した。
また、上記MRFによる学習は生データに対し多項式カーネルを用いたロジスティック回帰を学習することと同等であることを示し、最終的に提案手法が生データに対するロジスティック回帰に近しい精度であることを実験的に示した

問題設定

生データの各行(特徴ベクトル)とラベルを、$\{\boldsymbol{x}_i, y_i\}$とし、集約関数を$k(\boldsymbol{x})$とする。ここで集約関数は"任意の特徴量AとBの組み合わせがその特徴ベクトルに同時にTrueとなっている場合に1それ以外で0"を返す関数とする。この時集約関数集合を以下と定義する。

$$\mathcal{K}(\boldsymbol{x}):=(k(\boldsymbol{x}))_{k \in \mathcal{K}} \in\{0,1\}^{K}$$

ここで${K}$は集約関数の数を示す。
つまり$\mathcal{K}(\boldsymbol{x})$は生データの1行に$K$個の集約関数を適用してその結果を一つにまとめたベクトルになる。
参考画像は以下。

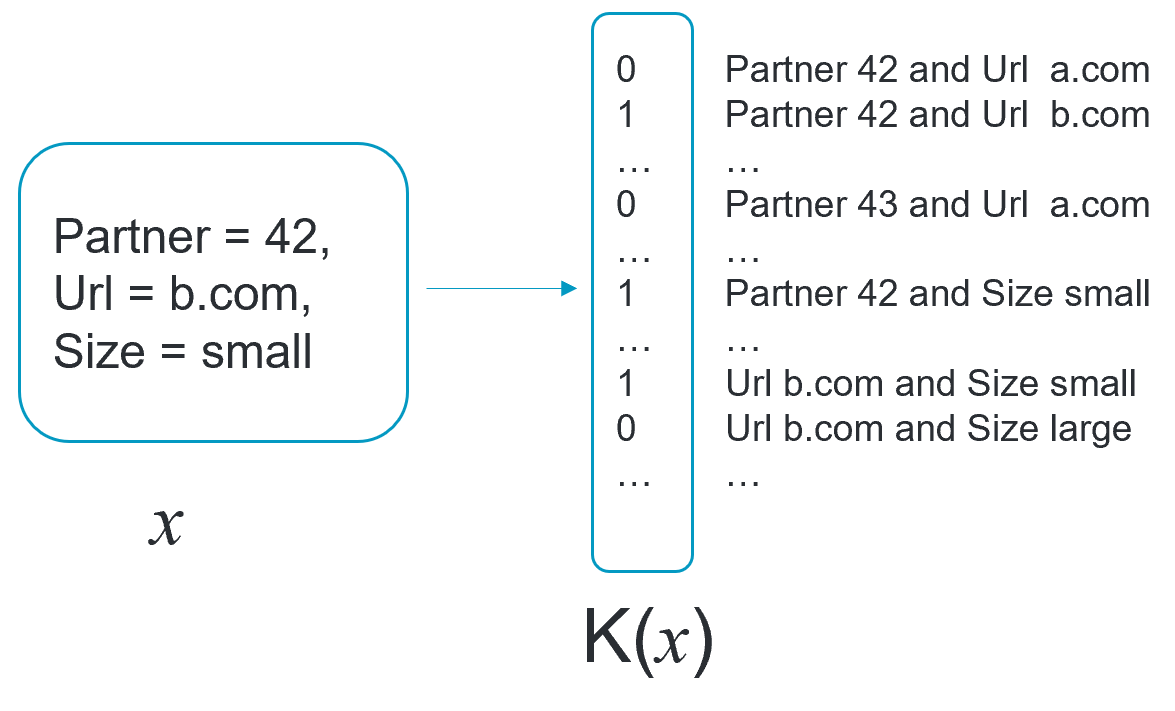
そして本論文における"集約データ"は以下で定義する。

$$\begin{aligned} \mathbf{c} & :=\sum_{i} \mathcal{K}\left(\boldsymbol{x}_{i}\right) \\ \mathbf{s} & :=\sum_{i} \mathcal{K}\left(\boldsymbol{x}_{i}\right) \cdot y_{i} \end{aligned}$$

ここで$\mathbf{c}$は生データ全行に対し集約関数を適用した結果のsum(特徴量の組み合わせの登場回数)であり、$\mathbf{s}$は各特徴量の組み合わせとy=1が共起した回数になる。
こうして得られた集約データからどうやってモデルを構築するか、というのが本論文の問題になる。

提案手法

本論文では上記集約データを入力都市、$\mathbb{P}(Y=y \mid X=x)$を推定する手法を提案している。そのためにまず同時分布を推定し、ベイズの定理を用いて上記条件付分布を導出する。この時初手で推定する同時分布は以下である。

$$\begin{equation*} \pi_{\mu}(\boldsymbol{x}, y) \equiv \frac{1}{Z_{\mu}} \exp \left(\mathcal{K}(\boldsymbol{x}) \cdot \mu_{c}+y \mathcal{K}(\boldsymbol{x}) \cdot \mu_{s}\right) \ \end{equation*} \tag{1}$$

ここで$\pi_{\mu}(x, y)$は特徴量とラベルの同時分布であり、MRFを用いて確率モデル化している。

• MRFはマルコフ性を仮定する生成的確率モデルであり、無向グラフで表現される。ノイズ除去等によく利用される。

$Z_{\mu}$は正規化定数であり、上記指数関数を確率に変換している。また、$\mu_c$と$\mu_s$はそれぞれパラメータである。上記同時分布を最大化するパラメータをMAP推定より定めることを学習と呼んでいる(対数尤度を勾配法で最適化する)。
そして条件付分布は以下で求められる。

$$\begin{align*} \pi_{\mu}(Y=1 \mid X=x) & =\frac{\pi_{\mu}(Y=1, X=x)}{\pi_{\mu}(Y=0, X=x)+\pi_{\mu}(Y=1, X=x)} \\ & =\sigma\left(\mathcal{K}(x) \cdot \mu_{s}\right) \tag{2} \end{align*}$$

ここで$\sigma$はシグモイド関数である。つまり提案手法により得られるモデルは、$\mathcal{K}()$を多項式カーネルとするロジスティック回帰を生データで直接学習したモデルと同等であることを示している。

実験結果

以下のモデルで検証を行い比較する。(和訳していないのはさぼり)

• $LR2$ is the logistic regression with second order kernel described in equation 8.
• $LR$ is a "vanilla" logistic regression without second order kernel.
• $MRF$ is the joined model trained from aggregated data described in this paper.
• $NB$ is a Naive Bayes classifier.

また、指標は以下である。(値が大きい方が望ましい)

$$N L L H \equiv \frac{\operatorname{LogLikelihood}(\operatorname{prediction}(X), Y)}{\operatorname{Entropy}(Y)}-1$$

上記設定で比較実験を行った結果は以下。

Model	NLLH train set	NLLH validation	best L2 parameter	run time
LR2	0.0991	0.0907	50.0	$2 \mathrm{~h}$
LR	0.0769	0.0757	8.0	$0.2 \mathrm{~h}$
MRF (50k samples)	0.0712	0.0681	400.0	$6 \mathrm{~h}$
MRF (400k samples)	0.0899	0.0869	400.0	$120 \mathrm{~h}$

提案手法がただのロジスティック回帰に勝利している点が確認できている。また、最もよい多項式カーネルロジスティック回帰に匹敵する精度が出ている。しかし他モデルと比較して学習時間が長い点が見て取れる。

所感

• 情報量が少なくなっているデータで学習したモデルが、生データで学習するレベルと同等に近い精度が出せているのはすごい
• 数式展開がきれい
• ロジスティック回帰はこの分野だと未だに現役
• さすがに時間かかりすぎでは？まだ実用には乏しい気がする
• 集約のやり方って他にどんな方法があるのか、連続値に対してはどうする？その辺に新しい課題ないか？