相互再帰関数の型付きクロージャ変換

はじめに

相互再帰関数のシンプルな型付きクロージャ変換を考案したので紹介する。このブログは、最終的に相互再帰関数の型付きクロージャ変換に行き着くために、クロージャ変換の各手法を図解して、その相違点を明確にしながら解説している。そのため、クロージャ変換のイントロ的な使い方もできると思う。

型付きクロージャ変換（Typed closure conversion）と呼ばれるものは[Minamide, 1995]が元になっていて、ここで多相型を含めた変換方法が示された。その後、拡張として[Morrisett, 1998]で再帰関数における3つの変換手法が示された。これらの研究はやがて、型付きアセンブリ言語（TAL）などの研究へとつながっている。しかし、相互再帰関数については明確に記述された文献が（私の知る限り）ない。だからといって、変換方法が自明であるかといえばそうではないと思う。実際に実装してみると、変換の単純さを保ちつつ、型付け関係を維持するのはそれほど簡単ではないことが分かった。
今回考案した相互再帰関数の型付きクロージャ変換は、既存のどんな変換方法よりシンプルであると確信している。しかも、ガーベジコレクションがしやすい。

クロージャ変換の目的

まず、クロージャ変換とは何だろうか。実際に実装を追ってみないとそのモチベーションを正確に捉えることは難しいと思われるが、主な目的は以下の２つである。

• 入れ子になった関数を除去する
• 高階関数（関数を引数に取る関数、関数を返す関数）を除去する

これらを実現できれば、クロージャはどのようなデータ構造でも良い。クロージャ変換の基本的なアイデアは、関数とその関数が使用される場所の環境をペアにすることだが、これをレコードやタプルとしてプログラムの一部として扱うのでも良いし、スタックやヒープ上の連続した番地に配置するのでも良い。タイガーブックでは静的リンクに基づく手法が示されている。

入れ子になった関数定義も、高階関数ももちろん機械語にはないため、ネイティブコードを生成する関数型言語の処理系ではどこかしらでクロージャ変換、あるいはそれに近いことを行っている。

ラムダリフティングとの違い

クロージャ変換との比較でよくラムダリフティング（Lambda lifting）という変換が登場する。ラムダリフティングとは、関数（ラムダ式）内の自由変数を引数に加えて、入れ子になった関数、あるいはラムダ式を除去するコンパイル手法である。ラムダリフティングをすると、クロージャ変換と同じように入れ子になった関数を全てトップレベルに持ち上げることができる。ただ、高階関数（関数を返す関数、関数を引数に取る関数）を扱うことができない。そのため、高階関数をサポートする言語ではラムダリフティングだけでは不十分である。
そのため、最近の関数型言語のコンパイラではラムダリフティングが用いられることは少ないが、[Graf, 2019]のように、自由変数を関数の引数として渡せるラムダリフティングはクロージャ変換に対して一定のパフォーマンスの向上が期待できるので、全く使い道がないわけではない。

たまにラムダリフティングを関数のトップレベルへの持ち上げに対する用語として扱っている例が見受けられるが、これは誤用だと個人的には思う。関数の持ち上げはしばしば Hoisting（これに対する通訳は知らない）と呼ばれる。ラムダリフティングの「リフティング」はあくまで自由変数の「持ち上げ」であって、関数の「持ち上げ」ではないと考えるべきだろう。

カリー化とクロージャ変換

Haskell に慣れすぎていると関数は暗黙にカリー化されていて、いつでも部分適用できるような気がしてしまうが、中間言語のレベルではカリー化は明示されていなければならない。ラムダ式が複数の引数を取れるとしても、例えば、((\x y -> x + y) 1) 2のような式はクロージャ変換やラムダリフティングをする段階ではエラーになる。クロージャ変換後には、関数の戻り値は、単純な値かクロージャでなければならないため、仮引数の個数と実引数の個数は常に一致していなければならない。

クロージャ変換の分類

クロージャ変換はいろんな表現の仕方がされる。これは基本的にはターゲット言語、あるいはターゲットマシンの仕様の違いによるものである。型付きクロージャ変換の説明では、基本的にターゲットはソース言語とほとんど同じ文法を持った中間言語であることが多いが、これは型付け意味論の証明をしやすくするためだろう。一方で、何かしらスタックモデルをターゲットする説明も多い。後者のメリットはクロージャを図解できることにある。本ブログでは、前者と後者の両方のアプローチを使って説明するので、状況に応じて相互変換して解釈していただきたい。

次に、クロージャの表現方法に二通りのアプローチがある。一つが Closure-passing スタイルであり、もう一つが Environment-passing スタイルである。Closure-passing では、関数の引数にクロージャ自体をとるが、Environment-passing では、環境のみを引数としてとる。

型無しラムダ計算のクロージャ変換

まずは最もシンプルなモデルとして、型無しラムダ計算に let 式を加えた言語で考える。

t ::= x | λx.t | t1 t2 | let x = t1 in t2

ターゲットの言語は以下のような構文を持つ。

e ::= x | λ(x1,...,xn).e | e(e1,...,en) | let x = e1; e2 | (e1,...,en) | let (x1,...,xn) = e1; e2

Environment-passing vs Closure-passing

クロージャ変換関数を[[・]]で表す。Environment-passing スタイル と Closure-passing スタイルとの違いは、ラムダ式と関数適用に現れる。以下がそのアルゴリズムである^[1]。ただし、y, z, ...は t に含まれる自由変数とする。

environment-passing-style

[[λx.t]] =
        let code = λ(env,x).
            let (y,z,...) = env;
            [[t]];
        (code,(y,z,...))
[[t1 t2]] =
        let (code,env) = [[t1]];
        code(env,[[t2]])

closure-passing-style

[[λx.t]] =
        let code = λ(cl,x).
            let (_,y,z,...) = cl in
            [[t]]
        in
        (code,y,z,...)
[[t1 t2]] =
        let cl = [[t1]] in
        let (code,_,...) = cl in
        code(cl,[[t2]])

これを図解すると、

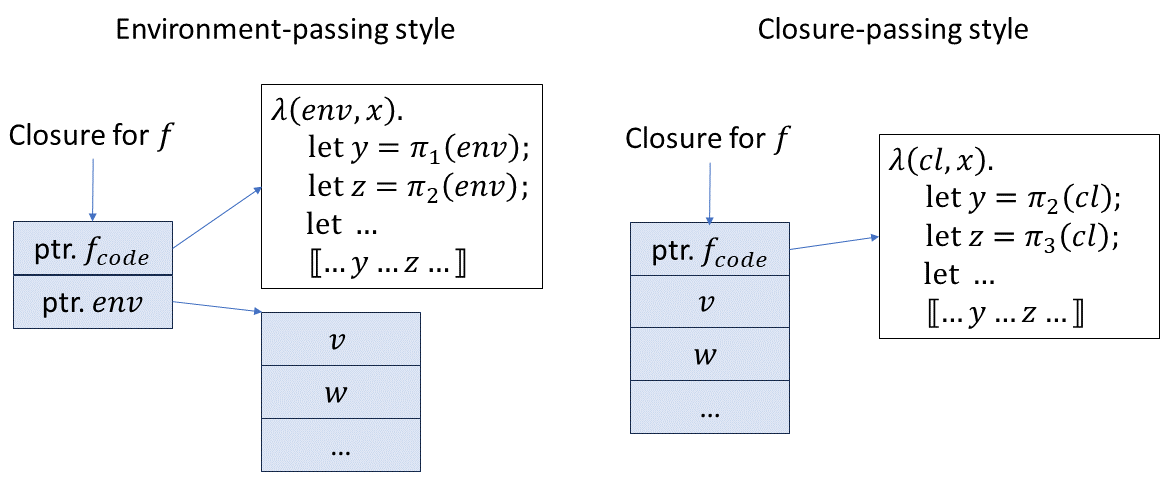
この図によると、Environment-passingとClosure-passingの違いは、コードポインタと環境が別の領域に配置されるか（Environment-passing）、コードポインタと自由変数が連続した領域に配置されるか（Closure-passing）の違いであることがわかる。環境を取り出すのに一つポインタを介さなくて良い分、（少なくともこのモデルでは）Closure-passingの方が効率的だと言える。
ちなみに、コードポインタと環境を別の領域に配置してもClosure-passingスタイルで書くことはできる。ただし、逆に、コードポインタと自由変数を連続した領域に配置しながら、Environment-passingで書く場合には、ポインタ算術が必要になるため、あまり好ましくない^[2]。

選択的クロージャ変換（Selective closure conversion）

自由変数のない関数にはクロージャを生成する必要がない。これを考慮したクロージャ変換を 選択的クロージャ変換 と呼ぶ^[3]。選択的クロージャ変換を行うと、生成されるコードサイズが削減され、実行速度の向上が期待できる。以下のような方法で実現できる。

• ラムダ式λx.tに対しては、tに自由変数が存在しない場合にクロージャを生成しないようにする。このような関数をKnown functionと呼ぶ。

• 関数適用t1 t2に対しては、[[t1]]がクロージャでない場合に[[t1]] [[t2]]を返せばよい。
  しかし、[[t1]]がクロージャであるか検査するには実装上、クロージャにタグをつけてクロージャかKnown functionかどうかを区別する必要がある。あるいは型によって区別するという方法もある^[4]。

Environment-passingスタイルでは自由変数がない場合、空の環境が生成されてしまい、環境の割り当てと取り出しに無駄が生じる。しかし、Closure-passingスタイルでは、自由変数がない場合、クロージャが単に長さ1のタプルになるだけであり、関数適用のときにクロージャから環境を取り出す必要もない。そのため、Closure-passingでは選択的クロージャ変換の必要があまりない。
また、選択的クロージャ変換は一般に型保存にならない。上で述べたように、実際に変換してみないとクロージャになるかならないかわからないためである。その意味でも、選択的クロージャ変換を必要としないClosure-passingスタイルに利点がある。

[Wand, 1994]ではSelective closure conversionの他にLightweight closure conversionというものも提案している。

選択的クロージャ変換の代わりに、一部の関数だけDefunctionalization^[5]するという手もある。

自己再帰関数のクロージャ変換

この節の内容は、[Morrisett et al, 1998]に基づいている。この論文は型付きクロージャ変換を自己再帰関数に拡張する目的で書かれているが、ここではまず型を無視して考える。

Environment-passingスタイル

まずは、Environment-passingスタイルを拡張する。Environment-passingの拡張には2つのアイデアがある。環境に再帰している関数のクロージャをとる（Fix-pack translation）か、とらないか（Fix-code translation）である。

Fix-codeは関数を再帰させているが、Fix-packはクロージャを再帰させている。そのためFix-packでは、新たにfixpackという構成子を用いて以下のようにクロージャを表現する。

$$\begin{aligned} \text{fixpack}\ f. (f_{code},\ env) \end{aligned}$$

Fix-codeは関数が呼び出される度に、クロージャを再構成しなければならないため非効率だが、一方でFix-packは、fixpack構成子をどのようにコンパイルするかが問題となる。相互再帰したクロージャのコンパイルも参照されたい。

Closure-passingスタイル

Closure-passingに対応する再帰関数のクロージャ変換は、Fix-type translationと呼ばれる。そもそも、Closure-passingスタイルでは、クロージャが再帰しているため変更点はない。

今の所、Fix-typeが3つの中で一番シンプルで効率的であるように見えるが、これを正しく型付けするには再帰型が必要となる。ref

相互再帰関数のクロージャ変換

いろいろなクロージャの割り当て方が考えられるが、とりあえず、Fix-code, Fix-pack, Fix-typeのそれぞれを直接的に拡張する方法を示す。

Fix-code translation (Shared closure)

関数定義のブロックが相互再帰する。Fix-codeの場合は、環境を共有するのが自然な構成である。そのため、相互再帰している関数の一つでもエスケープしていたら、クロージャも環境もGCがdeallocateできない。ただ、複数の関数が同じ自由変数を持っている場合は、環境を共有することでメモリを節約できるため、一概に非効率だとは言えない。

このモデルは独自にShared closureと呼んでいる。

Fix-pack translation (Shared environment)

Fix-packの場合も、環境を共有するのが自然だが、クロージャは分離させられる。そのため、クロージャが使用されなくなったら、クロージャの領域だけはGCできる。
ただ、共有された環境の問題点は、実装上、変換関数が汚くなってしまう点にある。クロージャ変換する前に、相互再帰している関数を走査して、自由変数を取り出し、それぞれのクロージャを構成しなければならない。また、再帰している関数の個数によって、環境の1つ目の値（図では$v$）までのオフセットが変わるため、これも変換関数を汚くする。

今度は環境のみを共有しているので、このモデルはShared environmentと呼んでいる。

Fix-type translation (Cyclic closure)

最後が大本命のFix-typeである。環境もクロージャも分離することができ、相互再帰している関数各々についてクロージャを生成することができる。また、同じ再帰ブロック内の関数は自由変数と同等に扱われるため、セルの何番目に配置されるかを気にする必要がなく、自己再帰関数と全く同じ方法で変換できる。さらに、クロージャが不要になったら、環境もろともGCできる。

このモデルは、環境もクロージャも共有せず循環参照しているので、個人的にCyclic closureと呼んでいる。

型付きクロージャ変換

単純型の型付きクロージャ変換

型付きクロージャ変換をする場合、ソース言語が単純型か多相型かにかかわらず、存在型が必要になる。実際、以下のように関数型の変換を書くと、型保存にならない。

$$\begin{aligned} \llbracket\tau_1\rightarrow\tau_2\rrbracket = ((\llbracket\Gamma\rrbracket, \llbracket\tau_1\rrbracket)\rightarrow\llbracket\tau_2\rrbracket) \times\llbracket\Gamma\rrbracket \end{aligned}$$

$\llbracket\cdot\rrbracket$は関数であるので、左辺に含まれない$\Gamma$が右辺に含まれてはならないのである。型保存の定義は

$$\begin{aligned} \Gamma \vdash t : \sigma \Rightarrow \llbracket\Gamma\rrbracket \vdash \llbracket t\rrbracket : \llbracket\sigma\rrbracket \end{aligned}$$

であるから、環境$\Gamma$と項$t$と型$\sigma$はそれぞれのスコープで変換されなければならない。

関数型の変換を型保存にするには、以下のように存在型を導入して環境を隠蔽する必要がある。

$$\begin{aligned} &\llbracket\tau_1 \rightarrow\tau_2\rrbracket = \exists t_{\text{env}}.((t_{\text{env}}, \llbracket\tau_1\rrbracket)\rightarrow\llbracket\tau_2\rrbracket) \times t_{\text{env}} \end{aligned}$$

Closure-passingスタイルの型付きクロージャ変換

Closure-passingでは、上のEnvironment-passingの技法に加えて、再帰型が必要になる。

$$\begin{aligned} &\llbracket\tau_1 \rightarrow\tau_2\rrbracket = \exists t_{\text{env}}. \mu t_{\text{cl}}.((t_{\text{cl}}, \llbracket\tau_1\rrbracket)\rightarrow\llbracket\tau_2\rrbracket) \times t_{\text{env}} \\ \end{aligned}$$

関数がクロージャを引数にとり、クロージャは関数を保持するという再帰的な関係があるためである。

また、コードポインタと自由変数を連続した領域に置く場合は、さらに列型（Row type）が必要になる。実際、上の定義だと、環境が$t_{\text{env}}$で型付けされなければならないため、コードポインタと同じレコードに入れることができない。
列型とは、以下で定義される型$R$のことである。ただし、$\epsilon$は空の列、$\rho$は列型変数を表している。

$$\begin{aligned} &\tau &&::= ...\ |\ \Pi R \\ &R &&::= \epsilon\ |\ \rho\ |\ \tau; R \end{aligned}$$

列型を用いると、クロージャの型は以下のようになる。

$$\begin{aligned} &\llbracket\tau_1 \rightarrow\tau_2\rrbracket = \exists t_{\text{env}}. \mu t_{\text{cl}}.\Pi ((t_{\text{cl}}, \llbracket\tau_1\rrbracket)\rightarrow\llbracket\tau_2\rrbracket) ; t_{\text{env}} \end{aligned}$$

多相型の型付きクロージャ変換

[Minamide et al, 1995]では、はじめに単純型付けのクロージャ変換をAbstract Closure Conversionによる方法で示し、その後にAbstract Closure Conversionと存在型を使った方法それぞれで、多相型に拡張している。Abstractというのは、クロージャ専用のデータ構造を構文に持たせているからだと考えられる。

この論文ではさらに、エスケープする型変数もクロージャにしてしまうという、Type-passingの手法をとっている。これは非常に強力であるが、型システムが複雑になる。型変数の環境に対してもpack/unpackをする必要があるため、カインドを導入する必要があったり、色々とややこしい。
その代わり、[Morrisett et al, 1999]ではType-erasure、すなわち型消去によってシンプルに型付けクロージャ変換をする方法を示している。

再帰関数の型付きクロージャ変換

前述の[Minamide et al, 1995]では再帰関数が含まれていなかったため、再帰関数のための型付きクロージャ変換を示したのが[Morrisett et al, 1998]である。この論文では既に紹介した3つの変換手法が示されている。
我々の関心はFix-typeなので、これの変換方法のみ以下に示す。（以下では列型を使っていないがほとんど変わらない）

これを、Cyclic closureモデルで相互再帰関数に拡張すれば、相互再帰関数の型付きクロージャ変換となる。先に説明したように、相互再帰している関数は自由変数と同じ扱いにできるため、型付け関係は変わらない。天下り的に説明してしまったので、どこが新奇性なのかわからないかもしれないが、例えば以下のようにFix-typeでShared Closureモデルにしてみるとより理解が深まるだろう。
このモデルではfとgのクロージャのレコードの1つ目と2つ目がコードポインタになっている。そのため、クロージャの型は、

$$\begin{aligned} \tau_{\text{cl}} = \mu t_{\text{cl}}.\Pi (t_{\text{cl}},\ \llbracket\tau_1\rrbracket\rightarrow\llbracket\tau_2\rrbracket);\ (t_{\text{cl}},\ \llbracket\tau_1^\prime\rrbracket\rightarrow\llbracket\tau_2^\prime\rrbracket);\ t_{\text{env}} \end{aligned}$$

のように再帰している関数の個数分だけ列型が大きくなる。そしてこの変換方法は非常に困ったことに型保存にならない。

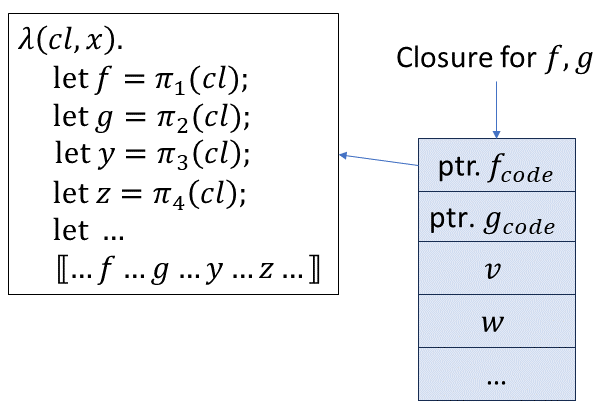
なぜなら、関数の型が同じ型を持てば、それらが定義されたletrecのブロック内で相互再帰している関数の個数にかかわらず、クロージャ変換後も同じ型を持たなければならないからである。
例えば、f : Int -> Intという関数がgと相互再帰していて、h : Int -> Intが自己再帰関数であるとき、fとhは同じ型をもつが、このクロージャ変換の後は異なった型を持ってしまう。
そのため、かなり工夫しないと型保存に相互再帰関数をクロージャ変換するのは難しい。

---

さらに、もう一つ問題がある。自己再帰の場合は上の式のようにfixが消えるため、そのまま低レベル言語にコンパイルすることができるが、Cyclic closureの場合はクロージャが相互再帰するためfixが消えない。つまり、

$$\begin{aligned} &\text{fix}\ &f = \text{pack} [\tau_{\Gamma_f},\ \text{roll}(\langle v_{\text{code}_f}, v_{\text{env}_f}\rangle\colon\tau_{{\text{cl}}_f})] \\ &&g = \text{pack} [\tau_{\Gamma_g},\ \text{roll}(\langle v_{\text{code}_g}, v_{\text{env}_g}\rangle\colon\tau_{{\text{cl}}_g})] \\ &... \end{aligned}$$

のようになる。これをコンパイルするには、例えば、fをヒープに割り当てるときに、gのところだけダミーの値を入れておき、gを割り当てたあとで、gを実際のポインタに更新するという方法が考えられる。しかし、gがfの中のどこに現れるかわからないため、実装はかなり複雑になる。次の節でこの問題の解決方法を示す。

相互再帰したクロージャのコンパイル

相互再帰したクロージャの割り当ては、Fix-packと相互再帰におけるFix-typeで発生する。ターゲット言語にfixpackなどの高水準な構成子があると、後々コンパイルが大変になる。そのため、クロージャ変換後のターゲット言語にmallocやupdate命令を追加して、ヒープのモデルを考える方が、実用上は有効である。
簡単のために自己再帰におけるfix-packの例で考えると、

$$\begin{aligned} \text{fixpack}\ f. (f_{code},\ env) \end{aligned}$$

のように変換するのではなく、

$$\begin{aligned} &\text{malloc}\quad env, [\textbf{ns}, v, w, ...] \\ &\text{malloc}\quad f, [f_{code},\ env] \\ &\text{update}\quad env(0), f \end{aligned}$$

とする。ここで、$\textbf{ns}$はnonsenseの略で、ダミーの値である。
このように直接ヒープに割り当てることで、ソースの情報を落とさずにコンパイルすることができる。

まとめ

シンプルなラムダ計算のクロージャ変換から、自己再帰関数、相互再帰関数、型付きへと拡張してきた。
そして、相互再帰関数のクロージャ変換では、Closure-passingスタイル、Fix-type translation、Cyclic closureモデルを用いるときれいに、しかも効率的に変換できることがわかった。

参考文献

• Appel. Continuation-Passing, Closure-Passing Style. (1989)
• Appel. Compiling with continuations. (1991)
• Wand. Selective and Lightweight closure conversion. (1994)
• Hannan. Type System for Closure Conversion. (1995)
• Minamide et al. Typed Closure Conversion. (1995)
• Morriset et al. Typed Closure Conversion For Recursively-Defined Functions. (1998)
• Appel. Modern Compiler Implementation in ML. (1998)
• Morriset et al. From System F to Typed Assembly Language. (1999)
• Appel. Efficient and Safe-for-Space Closure Conversion. (2000)
• Graf. Selective Lambda Lifting. (2019)

脚注

1. Type systems: Type-preserving closure conversion, https://gallium.inria.fr/~fpottier/mpri/cours04.pdf

2. Envieonment-passingでコードポインタと自由変数を連続した領域に配置してしまうと、環境を取り出すために隣のセルに移動しなければならないため、ポインタ算術が必要になる。ポインタ算術を使うと型付けが困難になるので、本稿においては適切なアプローチではない。スタックのセルをConsセルだと思うなら、パターンマッチによって隣のセルに動けるので問題ないが

3. Wand, 1994

4. Hannan, 1995

5. Reynolds. Definitional interpreters for higher-order programming languages. (1972). https://dl.acm.org/doi/10.1145/800194.805852