自作言語の紹介と関数型言語の実装方法の検討

はじめに

私が個人で昨年の 6 月ごろから開発している関数型プログラミング言語を紹介する。言語の名前は「Plato」である。

https://github.com/ksrky/Plato

この言語は昨年の U22 プログラミングコンテスト最終発表会でも発表した。コンテスト後、コンパイラの構成と実装に関して調査し直して、コードを一から書き直した。コンパイラは Haskell で書かれているため、本稿の内容も Haskell の知識をベースとしている。また、型理論の知識もある程度求められる。ただ、大雑把に書いているため、大雑把に読めばよく、このブログの読解に正確さは必要無い。
このブログでは、まず Plato のチュートリアルを示し、実際に何ができるのかを説明する。次に型検査や中間言語の仕様などコンパイラの実装手法を大まかに説明する。最後に今後実現したい機能などについて述べる。理論的に面白いものや有用な機能については、後日それ専用の記事を書く予定。

チュートリアル

インストール

READMEに同様の内容が書かれている。
Stack を使ってビルド＆インストールを行う。Cabal でもできるはず。
ghc のバージョンは 9.2.7、 9.2.8、 9.4.5 を想定している。GHC2021 で書いているため、最低でも ghc>=9.2 が必要。

$ git clone https://github.com/ksrky/Plato.git
$ cd Plato
$ stack install --stack-yaml=stack-a.b.c.yaml

下のようにバージョンが表示されればインストール完了。

$ plato --version
Plato version 1.0.0

削除したい場合は、platoという名前の実行ファイルだけを削除すればよい。

$ which plato
$ rm ~/.local/bin/plato

言語の概要

コンパイラと言っているが、現状 Plato コンパイラは中間言語への翻訳までしか実装されておらず、インタプリタ実行しかできない。
インタプリタは中間言語の項書き換えによって実装されている。
中間言語は依存型をもつ型付きラムダ計算をベースとしており、全ての束縛子に型注釈が加えられている。例えばラムダ式\x->tは\x:T.tという風に型Tが明示的に現れる。Plato コンパイラはこの中間言語をコア言語と呼んでおり、これに関してはコア言語の節で詳しく説明する。

コア言語は明示的に型付けされているが、表層言語はそうではない。プログラマは不要な型注釈を省略できる。しかし、Plato の型システムは$F_\omega$-like であり、任意階の多相型（Arbitrary-rank polymorphic types）を許しているため、型注釈を完全に省略することはできない。そのため、Plato ではトップレベルや let 式の束縛の中で宣言された関数や変数は型注釈を必須にしている。このようなトップレベルの型注釈を型署名（type signature）と呼ぶ。

Plato 言語の大きな特徴としてリテラルと入出力がないことが挙げられる。数値や文字列は扱えない。ブール値をビルトインとして扱いたくないため、if 文もない。これはコンパイラをできる限り単純にするという目的もあるが、もともと定理証明を目的としていたという背景がある。定理証明を目的とするのであれば、文字列や IO は必要なく、ただ型システムが利用できれば良い。インタプリタはせいぜいコンパイラの変換が意味論的に間違っていないかを確認する程度に利用しているに過ぎない。このような事情のため、Plato 言語の実用性はある程度犠牲にされている。しかし、逆にそうした制限された言語仕様の中でどれだけの表現性を生み出せるかというのは、実験する価値のあることだろう。

ファイルの拡張子は.plaである。プログラムファイルにはエントリポイントがない。宣言を記述するだけで式を評価することはできない。式を評価したい場合はコマンドラインツールと組み合わせて実行することになる。例えば、A.plaとB.plaというファイルで宣言された関数を利用して、式を評価したい場合、下のように対話的に実行することになる。

$ plato A.pla B.pla
>>

単一ファイルのコンパイルは次のように実行できる。これは現状、型検査に成功することを確認するだけのコマンドである。

$ plato run A.pla

実行例

試しに、Plato/examples配下のいくつかのプログラムを実行してみる。自然数はチャーチエンコーディングして表現する（しかない）。実行速度は相当遅いので、あまり大きな数を使わないように。

フィボナッチ数列の3番目と[2, 0, 1, 3]のクイックソートの計算

$ cd path/to/Plato
$ plato examples/fibonacci.pla examples/quick_sort.pla --libs libraries/base
>> fib (S (S (S Z)))
(`S, fold (`S, fold (`Z, `unit)))
>> qsort (S (S Z) :: Z :: S Z :: S (S (S Z)) :: Nil)
(`::, fold ((`Z, `unit), (`::, fold ((`S, fold (`Z, `unit)), (`::,
fold ((`S, fold (`S, fold (`Z, `unit))), (`::, fold ((`S, fold (`S,
fold (`S, fold (`Z, `unit)))), (`Nil, `unit)))))))))
>> :q

https://github.com/ksrky/Plato/blob/master/examples/fibonacci.pla
https://github.com/ksrky/Plato/blob/master/examples/quick_sort.pla

本来ならば、fib (S (S (S Z)))の結果はS (S Z))のように、
qsort (S (S Z) :: Z :: S Z :: S (S (S Z)) :: Nil)の結果は、Z :: S Z :: S (S Z) :: S (S (S Z)) :: Nilのように表示されてほしいが、今のところは出力をきれいに表示する機能を備えていない。これは、データコンストラクタのコア言語における扱いが特殊だからである（データ型の節で詳解）。見づらいが、規則に従って呼んでいけば、結果は間違っていないことが分かるだろう。

--libsオプションは--libs [PATHS..]でインポート可能なファイルのディレクトリを指定している。現在、ファイルのインポートは同じ階層のファイルしか許していないため、このようなオプションが必要である。
また上記の例で、SやZは libraries/base/Nat.pla で定義されており、対話環境にはインポートされていないため、本来スコープエラーになるのが自然である。しかし、現在の実装ではインポートされたファイルの宣言は import 文の位置にすべて展開されるため、quick_sort.plaの中でSやZが宣言されていることになり、これでもうまくいく。ファイルのインポートやモジュールシステムに関しては、モジュールシステムの節で詳しく議論する。

実装

関数型言語の実装方法に関して巷には十分な解説記事が少ないように感じるが、論文は十分にある。ここでは参考にした論文と、デザインの検討の過程を紹介する。ここに挙げたもの以外にも多くの資料を参考にしたが、特に論文全体が参考になったものを選んだ。GHC の Commentary や Agda のソースコードなども参考になった。

コンパイラの構成

コンパイラは以下の順にプログラムを処理する。

• 構文解析（compiler/Plato/Parsing）

  • レイアウトルールの適用

• 抽象構文木の整形（compiler/Plato/Nicifier）

  • 演算子の結合性解決

• 抽象構文から型検査専用構文への翻訳（compiler/Plato/PsToTyp）

  • スコープ検査
  • 構文制約の検査

• 型検査・カインド検査（compiler/Plato/Typing）

  • パターンマッチの変換

• 型検査専用構文からコア言語への翻訳（compiler/Plato/TypToCore）

• コア言語の評価（compiler/Plato/Interpreter）

コメントが少ないというのもあるが、全部で 5000 行弱で書かれている。

型検査・カインド検査

コア言語は明示的に型付けされていると述べたが、プログラマは型注釈を省略できるため、型検査器は型検査をすると同時に、欠落した型を付与しなければならない。これを型指向翻訳（type-directed translation）と呼ぶ。また、Plato 言語の特徴として、任意階の多相型を許していることがある。任意階の多相型システムの元では型注釈を完全に省略することはできないため、Plato 言語では型署名を必須にすることによりこれを解決している。
こうした言語機能は既に Haskell において実現されている。Haskell2010 では、RankNTypes 拡張を有効にすることで、任意階の多相型を利用できた（GHC2021 ではデフォルトで有効）。また、GHC は明示的に型付けされたコア言語を採用しており、この点も Plato と同様である。任意階の多相型システムの型検査、および型指向翻訳アルゴリズムは、GHC の主要開発メンバーである S. P. Jones らの論文 "Practical type inference for arbitrary-rank types" で実装付きで解説されている。Plato の型検査はほとんどこの実装をベースにしているが、主要な相違点といえば、型システムにデータ型を追加し、カインド推論を実装した点である。

型検査器の実装はcompiler/Plato/Typingに全て含まれている。「型推論器の実装」という題で型検査アルゴリズムについていくつか解説したので、そちらも参考にされたい。

https://zenn.dev/ksrk/articles/5e4a6858c43d6f

参考文献

• R. Milner. A theory of type polymorphism in programming. 1978.
• L. Damas and R. Milner. Principal type-schemes for functional programs. 1982.
• O. Lee and K. Yi. Proofs about a folklore let-polymorphic type inference algorithm. 1998
• S. Peyton Jones, D. Vytiniotis, S. Weirich, and M. Shields. Practical type inference for arbitrary-rank types. 2005.
• T. Schrijvers, S. Peyton Jones, M. Sulzmann, and D. Vytiniotis. Complete and decidable type inference for gadts. 2009.

コア言語

コア言語はほぼpisigmaという言語をそのまま使っている。これは依存型をもつ中間言語としての利用を目的とした言語である。Hackage に実装があがっており、これをほぼそのまま移植した。コア言語の構文は項と型の区別がない。これに似た型システムは Pure type system と呼ばれている。PiSigma は Pure type system に加えて、let 式や case 式、再帰型、ボックス化された値、ラベルの列などを含んでいる。ラベル列などがどのように利用されるのかすぐにはわからないと思うが、これはデータ型を表現するときに有用である。データ型で詳解する。

コア言語の構文を以下に示す。

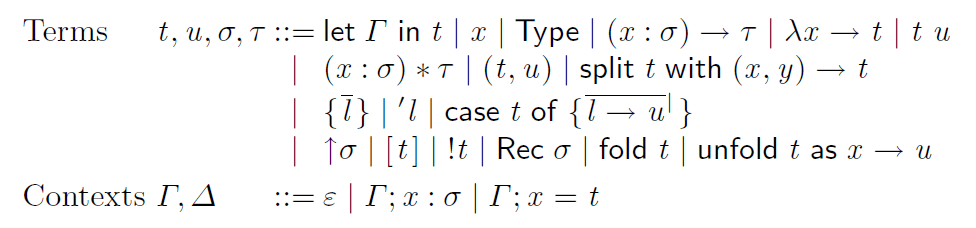
例えばチュートリアルで示したqsort関数は以下のようにコア言語で表される（手動でフォーマットした）。

$ plato run examples/quick_sort.pla --libs libraries/base --print-core
...
略
...
qsort_0 = \ $_975 : List_35 Nat_341 .
    split $_975 with (x_979, y_980) ->
        !case x_979 of {
            Nil -> [Nil_37 Nat_341];
            :: -> [split unfold y_980 as x_982 -> x_982 with ($_976, $_977) ->
                let {
                    smaller_12 : List_35 Nat_341;
                    larger_19 : List_35 Nat_341;
                    smaller_12 = filter_197 Nat_341 (>=_486 $_976) $_977;
                    larger_19 = filter_197 Nat_341 (<_432 $_976) $_977
                } in ++_46 Nat_341 (qsort_0 smaller_12) (::_40 Nat_341 $_976 (qsort_0 larger_19))]}

全ての束縛子（ラムダ式や Let 式など）に明示的に型注釈が加えられ、多相関数には型が適用されている。

参考文献

• T. Altenkirch, N. A. Danielsson, A. Löh, and N. Oury. ΠΣ: Dependent types without the sugar. 2010.

データ型

データ型の解釈は大きく分けて 2 つある。1 つ目が、型パラメータを受け取ってバリアント型を返す関数である。この解釈に則ると、例えばリスト型は以下のように表現できる。

$$\begin{aligned} List &= \lambda a.\ \langle Nil\ ()\ |\ Cons\ (a,\ List\ a) \rangle \end{aligned}$$

もう一つの解釈は、データ型をデータコンストラクタによってのみアクセスされる抽象型とみなすことである。この解釈に則ると、上記のリスト型は型コンストラクタもデータコンストラクタも本体を持たず、ただシグネチャだけを持つことになる。

$$\begin{aligned} List &: * \rightarrow * \\ Nil &: \Lambda a.\ List\ a \\ Cons &: \Lambda a.\ a \rightarrow List\ a \rightarrow List\ a \\ \end{aligned}$$

前者の解釈は、型の中身が分かっている点で transparent であり、また、List2 = Nil | Cons a (List2 a) という型とList型の表現が全く同じになってしまう点で applicative である。
一方で後者の解釈は、型の中身がわからないという点で opaque であり、また、上のList2とListが異なる型として扱われる点で generative である。
この解釈の違いはコンパイラのデザインに大きな影響を与える。

まず、前者の解釈に基づくと、パターンマッチに関する処理が扱いやすくなることが分かる。List 型のコンストラクタが Nil と Cons の 2 つだけであることが直ちにわかるため、パターンマッチが網羅的でなかった場合に警告を出したり、ワイルドカードパターンにコンストラクタを明示して変換するなどの処理が行える。

しかし、前者の解釈は構文を不必要に大きくしてしまう。まず、型に対してはバリアント型が必要になり、式に対してはバリアント型の各フィールドに対応するタグが必要になる。

data Type = ...
          | Variant [(Label, [Type])]

data Expr = ...
          | Tag Label [Expr] Type

また、このタグは型の一意性を保つために型を注釈しなければならない（例：<Nil ()> as List Nat）。これらは型検査において全く不要である。型検査・カインド検査においてはどちらもシグネチャのみに関心があり、その中身の実装が何であるかを知る必要はない。そのため、型検査においては後者の解釈が望ましい。加えて、後者の解釈では、List を型関数として扱う（型上で計算する）必要もなくなる。このように、データ型を抽象型として扱うことで、不要な構文や過剰に高レベルな型システムを扱わずに済む。

以上の議論から分かるように Plato コンパイラの型検査中の構文は後者の解釈を採用している。代わりにパターンマッチを処理する際には、データ型からデータコンストラクタの集合にマッピングする環境を型環境とは別に用意している。これによって、パターンマッチを処理する際に有効な前者の解釈を取り込んでいる。

データ型のコア表現

データ型は、データコンストラクタのラベル列と case 式の依存和で表される。以下にNatの場合の例を示す。

$$\begin{aligned} Nat &\colon \texttt{Type}& &= (l \colon {Z\ S}) ∗ \texttt{case}\ l\ \texttt{of} \{\ Z \rightarrow Unit\ |\ S \rightarrow Rec\ [Nat]\ \} \end{aligned}$$

Natを展開する例として、以下にadd関数を示す。

$$\begin{aligned} add &: Nat \rightarrow Nat \rightarrow Nat \\ add &= \lambda m\ n \rightarrow \texttt{split}\ m\ \texttt{with}\ (m_l,\ m_r) \rightarrow \\ &\quad\begin{aligned} &!\ \texttt{case}\ m_l\ \texttt{of}\ &&\{\ Z \rightarrow [n] \\ & &&|\ S \rightarrow [S\ (add\ (\texttt{unfold}\ m_r)\ n)]\ \} \end{aligned} \end{aligned}$$

まず split によって、Nat 型の値はラベルと case 式に分かれるが、このとき、ラベルによってパターンマッチが起こるため、結局コンストラクタのラベルとコンストラクタの引数が組として返される。また、コンストラクタの引数は暗黙的に再帰型を持つとして仮定されているため、unfold で展開しておく必要がある。コア言語として pisigma を選んだ理由の一つには、このパターンマッチのセマンティクスが最も洗練されているように思えたからである。

参考文献

• R. Harper and C. Stone. A Type-Theoretic Interpretation of Standard ML. 2000.
• J. C. Vanderwaart, D. Dreyer, L. Petersen, K. Crary, R. Harper, and P. Cheng. Typed compilation of recursive datatypes. 2003.

パターンマッチの変換

データ型の節で見たように、コア言語におけるパターンマッチは全て case 式によって、しかもパターンはコンストラクタと変数のみの引数によって表されなければならない。Haskell などの言語では以下に示すような関数宣言の引数でパターンマッチすることができるため、これも変換の対象となる。以下のnot関数の場合はパターンが 1 個だけであるため、case 式に変換するのは簡単である。

not True = False
not False = True

次に以下の関数定義はどうだろうか？まず、複数のパターンの列やワイルドカードパターンを含むため、すぐには変換方法が思い浮かばない。

S m < S n = m < n
Z < S _ = True
_ < Z = False

そこで、以下のようにコンストラクタを明示して、あり得るパターン全てを列挙してみる。

Z < Z = False
Z < S n = True
S m < Z = False
S m < S n = m < n

ただし、ここで First-match semantics を壊してしまわないように注意しなければならない。というのも、パターンに重複が合った場合、パターンの順序を入れ替えてしまうと適用される句^[1]（clause）が異なってしまうことがあるからである。そのため、パターンを上から見ていって最初にマッチしたものの句を採用する（First-match semantics）場合、パターンの順序の入れ替えには注意を払わなければならない。あり得るパターンを全て列挙した後は句の順序は問題にならない。
上のように変換してしまえば、後はシンプルに case 式のみを含む式に変換することができるだろう。

(<) = \x y -> case x of
	Z -> case y of
		Z -> False
		S n -> True
	S m -> case y of
		Z -> False
		S n -> m < n

コンストラクタを全て明示するという変換方法のアイデアは依存パターンマッチ [Cockx and Abel, 2018]からとった。これは決定木法と呼ばれる。[Jones, 1987]ではワイルドカードパターンを残したまま、それをパターンマッチに失敗した時のデフォルトとして利用する変換方法（バックトラック法）を紹介しているが、この方法では case 式が深くネストしてしまったりして、直感的な変換結果が得られない。[Augustsson, 1985]も同様である。コンストラクタパターンのみを許すことによって、一つの case 式に対し、全通りのパターンマッチが行える。
しかし、コンストラクタを明示する方法にも欠点があり、N 個のコンストラクタの中から 1 つだけ取り出すようなパターンマッチのときに、２本のパターンマッチで済んでいたものをわざわざ N 個に拡大しなければならないといった問題がある。ただ、コンストラクタを 10 個以上もつデータ型などはそれほど多くなく、関数の引数のパターンの並びも（変数パターンを除けば）せいぜい 2 つ程度であるので case 木が極端に肥大化することはないと考えた。

他にもネストしたパターンや変数のみのパターンの削除などの処理が必要となる。詳しくはcompiler/Plato/Typing/PatTrans.hsを参照されたい。URL から分かるように、パターンマッチの変換は型検査モジュールに含まれている。これは構文木の走査回数を減らすためと、変換中に型に対する操作を含むためである。

参考文献

• L. Augustsson. Compiling pattern matching. 1985.
• S. L. Peyton Jones. The Implementation of Functional Programming Language. 1987.
• J. Cockx and A. Abel. Elaborating dependent (co)pattern matching. 2018.

構文解析とその周辺

構文解析について長々と説明しても退屈であるため、ここでは大きなトピックについてのみオムニバスに紹介する。

まずは、レイアウトルールである。Plato のレイアウトルール（またはオフサイドルール）は Haskell とほとんど同じ定義である。Haskell2010 Language Reportを参考にした。

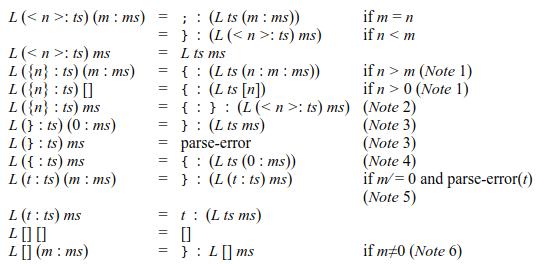
ただし、この定義からアルゴリズムを導き出すことはできない。レイアウトルールは、レキサーとパーサーの両方にまたがるため、結局アドホックな実装にならざるを得ない。レイアウトルールそのものを LR パーサーのような宣言的定義に含めるようにしようという試みもある。"Principled Parsing for Indentation-Sensitive Languages: Revisiting Landin's Offside Rule, M. D. Adams, 2013" によると、Haskell 製のパーサージェネレータである Happy を改良して、そのような構文解析を可能にしたが、まだ実用には至っていないようだ。
レイアウトルールの実装は以下のブログで解説している。
https://zenn.dev/ksrk/articles/e3ec05ea3d9809

もう一つ、Haskell の構文的に有用な特徴として、ユーザー定義の演算子がある。これは演算子を関数として定義し、その結合性を後から指定できるようにする機能である。残念ながら、構文解析をする前に演算子の結合性を決定することは不可能なので、パーサージェネレータによって生成された構文解析の後に再び、演算子の結合性解決の処理が必要となる。実装上は、中置式を一旦全て左結合として解析し、再度それを展開することで、同じ抽象構文上で処理することが可能となる。演算子の結合性解決アルゴリズムは、Language Report の10.6 節で実装付きで紹介されている。
Plato では、演算子の結合性解決はNicifierというモジュールに組み込まれている。Nicifier は、値レベルの式、型レベルの式、パターンに含まれる演算子の結合性解決のほか、相互再帰の検出や宣言の順序の組み替えなどを行い、内部言語の意味論を扱いやすくさせる役割を持つ。Nicify という用語は Agda のコンパイルプロセスから取った。

他に構文解析が終わってから、型検査が始まる前にしておくべき処理は何だろうか。まだ、この時点で検出できていない構文エラーがある。Haskell の場合、以下のようなものが例に挙げられる。

• データコンストラクタの名前の一意性
• トップレベルで定義された関数の名前の一意性
• 関数の引数パターンに現れる変数の名前に重複がないか

これらは構文解析で検出することができない。しかし、かといって、これらが保証されなくても、意味論が壊れることはない（妥当な意味論を設定できる）。例えば、f x x = xという関数定義があったとして、右辺に現れるxはより近い場所で束縛された二番目の引数を参照するということを保証すれば、引数に重複があっても問題にならない。しかし、このような関数定義は Haskell ではエラーになる。その理由を推察するなら、プログラマが予期しないバグに出会うのを防ぐためだろう。データコンストラクタの名前や関数の名前の一意性も、前の定義をシャドウイングすることで意味論的には問題にならない。しかし、Haskell では並列に定義された識別子は対等に扱うというのがベースの設計思想にあるようだ。これらのような構文上のルールを SML Definition に倣って構文的制約（Syntactic Restriction）と呼ぶ。

今後実装したい機能

依存型

Plato 言語は証明支援系を目指して開発を始めたという背景があるが、今のところはプログラミング言語としての機能の拡充を優先している。ただ、将来的には依存型を導入したいと考えている。依存型の前段階として、まずは GADT をサポートするだろう。GADT を導入するにはまず、コア言語に型の等価性を判断する構文を加えなければならない。さらに型推論では、現在の型環境に加えて型に関する制約を保持する必要がある。

依存型システムには魅力があるが、あまり強力な依存型を導入してしまうと、コンパイラの複雑さ以前に、プログラミングの複雑さが増大してしまう。それに既にそこには Coq や Agda といった競合があるため、Plato では弱めの依存型を導入して実用を重視した言語を目指そうと考えている。証明支援と言うよりは型駆動開発に比重をおいた言語である。

モジュールシステム

Plato 言語は型システムの強さ（型付けできる項の種類や推論能力）でいえば Haskell に引けを取らない能力を備えているが、表現力はその半分にも満たないように思われる。その理由の一つに型クラスがないことが挙げられる。実際、仮に Haskell の Prelude モジュールの中で型クラスに関わる要素が全て削除されてしまったら、恐らく半分近くの関数がなくなってしまうだろう。しかし、型クラスは利便性の反面、型システムを一気に複雑にしてしまう。本言語は実験目的で開発しているため、型システムの挙動が追いきれなくなると困る。そこで、型クラスの代わりに ML のモジュールシステムによってアドホック多相を実現してみようと思う。
Haskell でいうモジュールシステムと ML のモジュールシステムはほとんど意味が異なる。Haskell のモジュールはほぼ単一ファイルのことであるが、ML のモジュールは型クラスと同じように似たプログラムをまとめて抽象化する仕組みである。モジュール（正確にはファンクタ）と依存積型を組み合わせると、Haskell の型クラスを模倣するプログラムが書けるようになる。以下がその例である。

$$\begin{aligned} &Monad &\colon &\Pi M \colon \texttt{Type} \rightarrow \texttt{Type}.\ \Pi monadM \colon MonadT\ M.\\ &&&\quad\{return \colon \Pi A\colon \texttt{Type}.\ A \rightarrow M\ A,\\ &&&\quad\ bind \colon \Pi A\colon \texttt{Type}.\ \Pi B\colon \texttt{Type}.\ M\ A \rightarrow (A \rightarrow M\ B) \rightarrow M\ B\} \\ &Monad &=\ &\lambda M\colon Type \rightarrow Type.\\ &&&\quad\ \lambda monadM \colon MonadT\ M.\ \texttt{case}\ monadM\ \texttt{of}\ \{\\ &&&\quad\quad MonadT\ ret\ bnd \rightarrow \{return = ret,\ bind = bnd\}\\ &&&\quad\} \end{aligned}$$

これを Plato の拡張された構文上で実装してみると以下のようになるだろう。

Monad.pla

-- Monadのインスタンスを定義するためのデータ型
data MonadT m where
    MonadT : ({a} a -> m a)
        -> ({a b} m a -> (a -> m b) -> m b)
        -> MonadT m

monadReturn : {m} MonadT m -> {a} a -> m a
monadReturn (MonadT r _) = r

monadBind : {m} MonadT m -> {a b} m a -> (a -> m b) -> m b
monadBind (MonadT _ b) = b

-- これがHaskellの型クラスに対応するモジュール
-- 型変数 m は推論される
-- monadはインスタンスの定義
module Monad {m} (monad : MonadT m) where
    infixl 1 >>=
    infixr 1 >>
    infixr 1 =<<
    infixr 1 >=>

    return : {a} a -> m a
    return = monadReturn monad

    (>>=) : {a b} m a -> (a -> m b) -> m b
    (>>=) = monadBind monad

    (>>) : {a b} m a -> m b -> m b
    ma >> mb = ma >>= \_ -> mb

    (=<<) : {a b} (a -> m b) -> m a -> m b
    (=<<) = flip (>>=)

-- Maybeモナドのインスタンスの定義
monadMaybe : MonadT Maybe
monadMaybe = MonadT Just bind
  where
    bind : {a b} Maybe a -> (a -> Maybe b) -> Maybe b
    bind Nothing _ = Nothing
    bind (Just x) f = f x

-- Eitherモナドのインスタンスの定義
monadEither : MonadT Either
monadEither = MonadT Right bind
  where
    bind : {a b} Either a b -> (b -> Either a b) -> Either a b
    bind (Left l) _ = Left l
    bind (Right r) f = f r

module MonadMaybe = Monad monadMaybe

module MonadEither = Monad monadEither

この定義に基づくと、MonadMaybe.returnがMaybeに対するreturn関数となる。厳密な意味でのアドホック多相は実現できていないため、モジュールで修飾する必要があるが、 open ディレクティブを用いる（open MonadMaybe）ことで、returnをそのまま扱える。ただし、open MonadEitherなどと併用するとreturnの型が曖昧になるため、型検査に失敗する。

おわりに

このブログを書いたのは自分の活動記録を残すということもそうだが、言語開発に詳しい方の意見を伺いたいという意図もある。そのため、もしバグやらその他問題点を発見し、それを報告する余裕のある方がいれば、連絡いただけると大いに助かる。

脚注

1. 句（clause）というのはオリジナルな命名で、これが適切かどうかはわからないが、Z < Z = Falseのような 1 行の関数定義のことを指している。