🚀
宇宙からの地球観測第３章地球を回る人工衛星の運動と座標系

2024/04/29に公開
Python
宇宙からの地球観測　第3章の章末問題は一見して難しいだろうと想像つきます。問題文が短いからです。

 問題3.1式3.13 の第一式を導きなさい
\sin \delta = \sin I \sin \phi
\sin(\alpha - \Omega) = \cot I \tan \delta
\cos(\alpha - \Omega) = \cos \phi \sec \delta

 基本用語の理解式3.13 の意味がまったくわかりません。

色々検索してみると、どうやら球面三角法の背景知識が必要なようです。
wiki:球面三角法
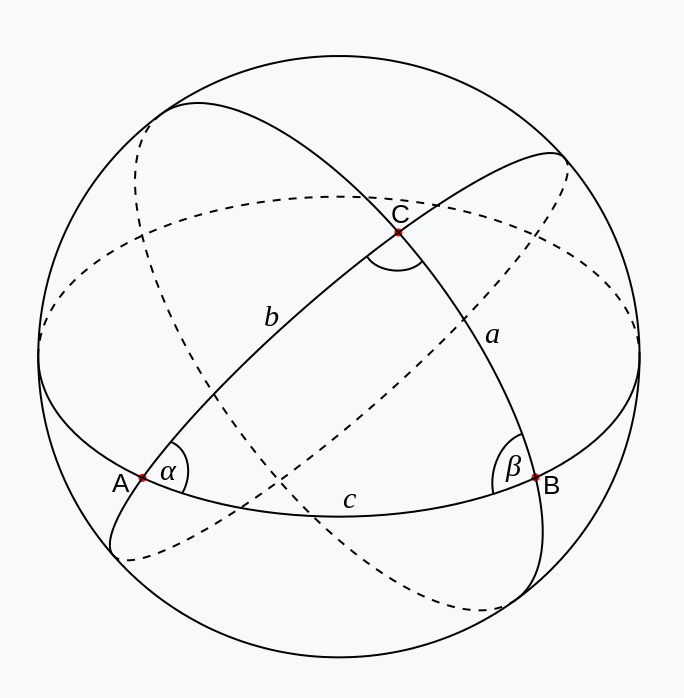
球面上に2点A,Bがあるとき、この2点と球の中心を通る平面で切断したときの断面に現れる円が大円であり、このときの大円上の弧ABを球面多角形においては辺と呼ぶ。 通常、球の半径は1とするので、辺の長さはその辺を含む大円における中心角の弧度法表示と一致する。

なるほど、角度と辺の長さが一致するというのがとても面白いですね。
直角球面三角形

天文学や航海術では一つの角が直角の場合が多く、この場合公式は簡単になる

R2 \sin a= \sin A \sin c
まさにこれですね。

本書の中での式　\sin \delta = \sin I \sin \phi　において

\deltaは赤緯（地心からみて衛星が赤道面と何度のところにあるか）、　Iは軌道傾斜角（軌道面が赤道面となす角で反時計回りに測った角度）、 \phiは緯度引数:(軌道面上での赤道昇降点から現在位置までの中心からの角度）とのこと。

自分の頭を整理するために図で書いてみました。

Aが地球の中心、Bが衛星がいる場所　Dが昇降点　Eが衛星から赤道面に垂線をおろした場所、FはEからADに垂線をおろした場所、CがAE延長して地球表面との交点です。

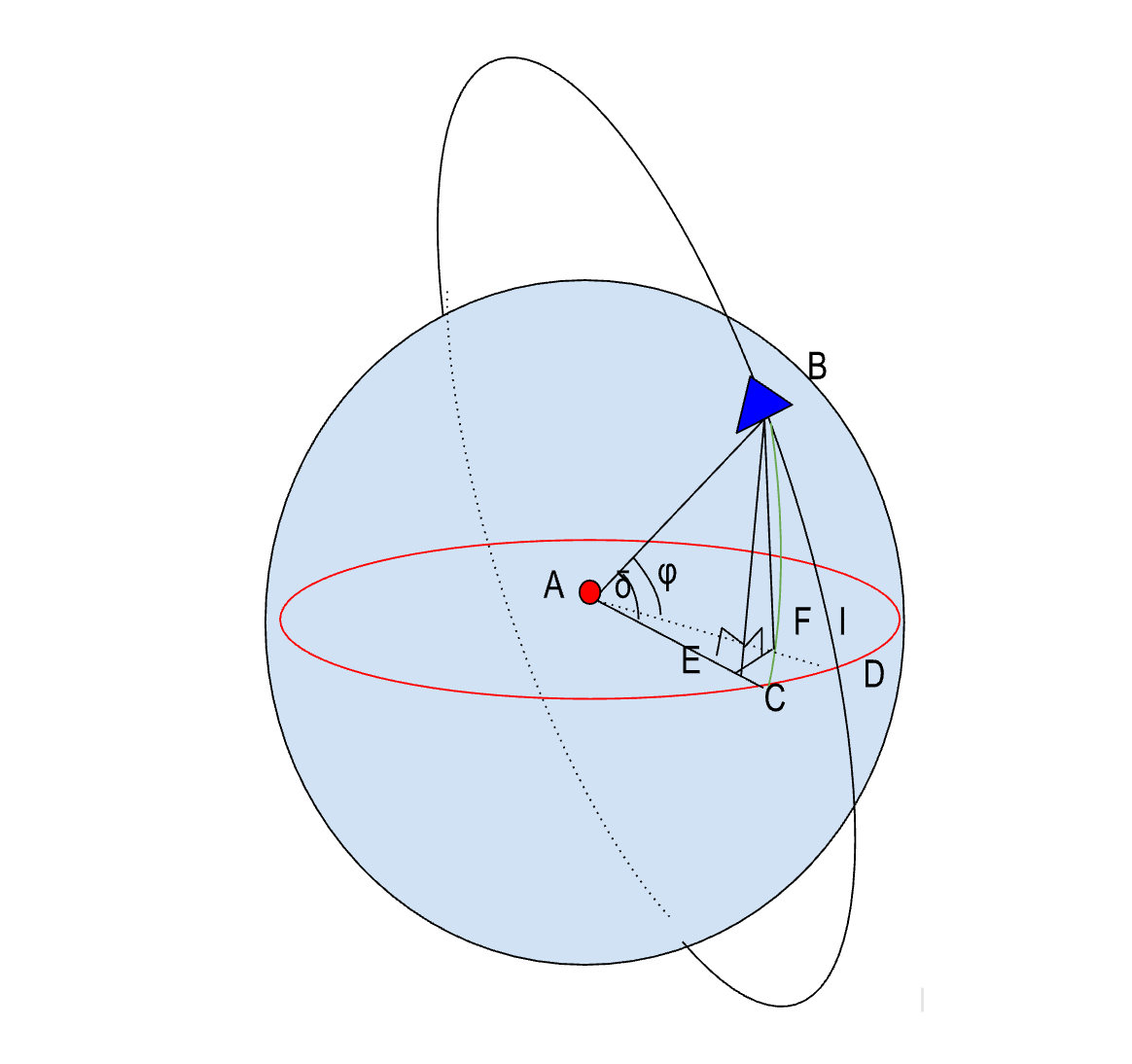
 回答3.1起動の半径を１として、の球から切り出される直角三角形BEA, BEFの関係をると,

\angle BEF= \angle BEA = {\pi \over 2}

I=傾斜角なので、

\angle BFE = \pi  - I

\angle FBE =  \pi - {\pi \over 2} - (\pi - I) = I- {\pi \over 2}
\sin \delta = BE = BF \cos( \angle FBE : I-{\phi \over 2})
三角関数公式: https://manabitimes.jp/math/660

負角の公式

\cos -\theta = \cos \theta より

\cos I-{\phi \over 2} = \cos {\phi \over 2} - I

補角の公式

\cos(90-\theta)=\sin(\theta) より

\cos ({\phi \over 2} - I)= \sin (I)

また、

BF=\sin \phi
よって下記が導けました

\sin \delta = \sin I \sin \phi
天体の位置を地平座標系（観測者の真上の方向＝天頂 (zenith) と、天頂を通り南北を結ぶ大円＝子午線により定義される。観測者を通り、観測者から天頂に向かう方向に垂直な平面により、地平線(horizon)を定義。）から赤道座標系（地球の自転軸を基準にした座標系、地球の赤道を基準とする）へ変換する際に使用される三つの数学的な式が示されています。
参考：https://eco.mtk.nao.ac.jp/koyomi/wiki/BAC2C9B8B7CF2FC3CFCABFBAC2C9B8B7CFA4C8C0D6C6BBBAC2C9B8B7CF.html

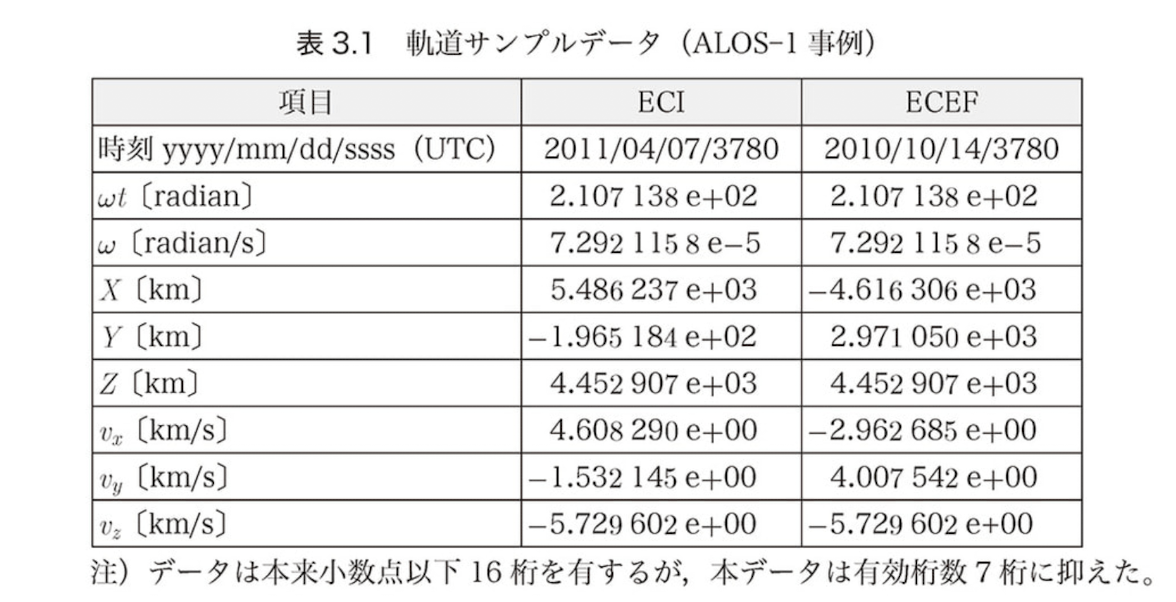
 問題3.2表3.1の ECI, ECEFの変換を確認しなさい


 言葉の理解素人には表をみただけではさっぱり分からないので、第３章を読み進めて

ECI, ECEF, 座標変換について理解を進めます。

 座標系についてECI（Earth-Centered Inertial）：

慣性系で、地球の重心を中心にしていますが、地球の自転は考慮しません。恒星に対して固定された座標系とみなされます。
ECEF（Earth-Centered Earth-Fixed）：

地球の自転と同期している座標系で、地球の重心を中心にして地表とともに回転します。

 変換プロセス時間の調整：

ECEF座標系は地球の自転に依存するため、時刻をUTCまたはGPS時に同期させる必要があります。変換には、変換を行う正確な時刻が必要です。
回転行列の計算：

地球の自転を表す回転行列を計算するために、グリニッジ恒星時（Greenwich Sidereal Time, GST）または地球回転角（Earth Rotation Angle, ERA）を計算します。これは地球の自転角度で、UT1やUTCといった時刻尺度から導出されます。
座標の回転：

ECI座標系の位置と速度ベクトルをECEF座標系に変換するために、回転行列を使用して座標を回転させます。これは、地球の自転による回転を座標変換に適用することに相当します。
極運動の補正：

ECEF座標系は地球表面に固定されているため、極運動（地球の極のわずかな動き）による補正も考慮する必要があります。このため、国際地球回転・基準系サービス（IERS）から提供される極運動データを使用します。
最終的な座標の変換：

補正された回転行列と極運動データを使用して、ECI座標系からECEF座標系への最終的な変換を行います。

 数式第三章 (3.28)

一般に、ECEF座標 (X', Y', Z') はECI座標 (X, Y, Z) から以下のように計算されます：

\begin{bmatrix}
X' \\
Y' \\
Z'
\end{bmatrix}
=
R
\begin{bmatrix}
X \\
Y \\
Z
\end{bmatrix}
ここで、R は地球の自転を表す回転行列です。
 R =\begin{bmatrix}
\cos{\omega t} & \sin{\omega t} & 0\\
-\sin{\omega t} & \cos{\omega t} & 0\\
0 & 0 & 1\\
\end{bmatrix}
速度ベクトルも同様に、角速度を考慮した回転により変換されます。

ここでr_1はECIでの位置ベクトルです。
第３章(3.33)

\bar{\omega} = \begin{bmatrix} 0 \\ 0 \\ \omega \end{bmatrix}
速度　(3.34)

v_2 = v_1 - \bar{\omega} * r_1
加速度　(3.35)

a_2 = a_1 - 2\bar{\omega}*v_1 + \bar{\omega} * \bar{\omega} * r_1

 回答3.2上記問題3.1 に記載した表の１行目の時刻が２列でちがうのは理解ができていません。そこは無視をするとして２行目の \omega t [radian]はその時点での地球の自転角度、３行目の \omega [radian/s]が自転速度を表しているということが分かりました。この２つがわかればどちらかから、もう一方を計算することができそうです。
import numpy as np
import math

# 地球の自転速度（角速度）をラジアン/秒で定義
EARTH_ROTATION_RATE = 7.2921158e-5  # rad/s

def to_radians(degrees):
    return degrees * math.pi / 180

def to_deg(rad):
    return rad * 180/math.pi 


def eci_to_ecef(eci_coords, eci_velocity, gst):
    """
    ECEF座標系からECI座標系への変換を行う。    
    :param ecicoords: ECI座標系での位置ベクトル (x, y, z) [km]
    :param eci_velocity: ECI座標系での速度ベクトル (vx, vy, vz) [km/s]
    :param gst: グリニッジ恒星時 [rad]
    :return: ECEF座標系での位置ベクトルと速度ベクトル
    """
    # 回転行列（Z軸周りの回転）
    rotation_matrix = np.array([
        [np.cos(gst), np.sin(gst), 0],
        [-np.sin(gst), np.cos(gst), 0],
        [0, 0, 1]
    ])    
    # 座標変換
    ecef_coords = np.dot(rotation_matrix, eci_coords)    
    # 速度に対する回転の影響を考慮
    omega_matrix = np.array([0, 0, EARTH_ROTATION_RATE])  # rad/s
    # 速度変換
    ecef_velocity = eci_velocity  - np.cross(omega_matrix,eci_coords)   
    return ecef_coords, ecef_velocity


gst = to_radians(2.107138e+02)

# 例：ECI座標と速度
eci_coords = np.array([5.486237e+03, -1.965184e+02,4.452907e+03])  # km
eci_velocity = np.array([4.608290, -1.532145,-5.729602])  # km/s

# 座標変換
ecef_coords, ecef_velocity = eci_to_ecef(eci_coords, eci_velocity, gst)

print("ECEF Coordinates:", ecef_coords)
print("ECEF Velocity:", ecef_velocity)
--
ECEF Coordinates: [-4616.30681041  2971.04818774  4452.907     ]
ECEF Velocity: [ 4.59395965 -1.93220776 -5.729602  ]
最初計算するとまったく変換結果があわなかったのですが、

\omega tの値がradにしてはずいぶん大きいなとおもい、試しに 角度としてradに変換するとうまく変換が一致しました。

（この本誤植がそこそこある気がします。）
速度の方は、変換した結果と表ECEFの値が一致しません。色々考えましたが一旦Giveupします。

 問題3.3式3.8, 3.10から C(r)をもとめなさい

(3.8)

\dfrac{1}{2}v^2 - \dfrac{MG}{r}=C(r)

ｒは地球中心から衛星までの距離　v は衛星の速さ　Mは地球の質量、Gは重力定数
C(r)は時間に依存しない関数で、運動エネルギーと位置エネルギーの和が一定であることを表す。

(3.10)
m\dfrac{v^2}{r} = mg_0(\dfrac{r-h}{r})^2 = \dfrac{GMm}{r^2}
v=(r-h)\sqrt{\dfrac{g_0}{r}} = \sqrt{\dfrac{GM}{r}}

ｍは人工衛星の質量　h は人工衛星の高度　g_0 地球表面の重力加速度

GMは重力定数と地球質量の積

 言葉の理解慣性座標系内ではニュートンの運動方程式が成立する

第一法則：物体は力が加わらない限り同じ速度で動き続ける

第二法則：力は質量と加速度の積である

第三法則：作用と反作用は大きさが等しく作用の方向が反対である

 重力定数万有引力の公式を知っている必要がある:

https://manabitimes.jp/physics/2379
万有引力の公式

質量 M，mの2質点の間には，万有引力が働く。2点の距離を

rとするとき，万有引力の大きさは

F=G\dfrac{Mm}{r^2}

 人工衛星におけるエネルギー保存の法則式3.8 は、衛星の運動エネルギーと重力ポテンシャルエネルギーの和が一定であることを表すとありますが、どういう意味なのかいまいちピントきません。GPTにわかりやすい解説をお願いしてみました。
力学の「エネルギー保存の法則」を示しています。この法則は特に閉じた系で、外部からの力が働かない場合に成立します。
式は次のようになります：
 \frac{1}{2}v^2 - \frac{MG}{r} = C(r) ここで、

\frac{1}{2}v^2 は衛星の運動エネルギーを示します。ここで v は衛星の速度です。

\frac{MG}{r} は地球の重力ポテンシャルエネルギーを示しており、M は地球の質量、G は万有引力定数、r は地球中心から衛星までの距離です。

C(r) は特定の軌道に固有のエネルギーの定数で、その軌道におけるエネルギー保存の総和です。
この式の右辺の定数 C(r) は、実際には定数ではなく、特定の軌道において保存されるエネルギーの量を表しています。一般に、この定数は軌道における特定のポイント（例えば近地点や遠地点）での速度と位置から計算されます。
この式からわかることは、衛星の速度が増加すれば（運動エネルギーが増加すれば）、ポテンシャルエネルギーが減少する（つまり、衛星が地球から遠ざかる）ということです。逆に、衛星が地球に近づく（ポテンシャルエネルギーが増加する）場合、速度は減少します。
実際には、このエネルギー保存の法則は、衛星の軌道を設計したり、既存の軌道の動きを解析したりする際に重要です。さらに詳細な分析では、軌道が時間と共にどのように変化するかを見るために、衛星の位置、速度、加速度などを含む微分方程式を解く必要があります。

 第一宇宙速度こちらの解説が本書よりもさらにわかりやすかったです。

https://manabitimes.jp/physics/1880

式3.10 は、人工衛星の遠心力と、重力がつりあっている、つまり落下もせず、遠くにもいかない速度のことを説明しているということが理解できました。

 回答3.33.8のvに3.10 を代入します。

\dfrac{GM}{2r}-\dfrac{MG}{r} = C(r)

よって、C(r)=-\dfrac{GM}{2r}であることがわかりました。

これは地球の周りを周回している人工衛星における、エネルギーの総和は重力定数X地球質量 (398601*10^9 m^3/s^2) を地球中心からの距離の２倍で割ったものということですね。マイナスが付いているのは引力と打ち消すという意味と理解しています。
問題3.1

基本用語の理解

回答3.1

問題3.2

言葉の理解

座標系について

変換プロセス

数式

回答3.2

問題3.3

言葉の理解

重力定数

人工衛星におけるエネルギー保存の法則

第一宇宙速度

回答3.3

Discussion
