波と虚数とフーリエ変換

SAR衛星などでつかわれるMicro波といった電気信号は波です。
そして波を表す数式には当たり前のように虚数の式が出てきます。
これはいったん何を表しているのか最初まったく理解できませんでした。
わかりやすく美しい解説、　わかりやすい本　をみつけ、何回も読んでようやく輪郭がつかめてきました。

波をあらわす数式は？

波を表す性質として　どのくらい大きい波かという振幅と、どのくらい細かく揺れるかという周波数が重要になってきます。さらに波の中のどこに位置するかを表すものが位相です。
波は繰り返しおなじ形がくりかえします。例えば下記のBの位置は何度も発生します。全体のどこにいるかというよりも、波の中でどこにいるのかという情報が重要になります。それが位相です。

そして高校で習った三角関数をつかうと、波を数式で表現することができます。
以下のプログラムではsin関数だけをつかうことで波を描画します。

import numpy as np
import matplotlib.pyplot as plt

# 波形のパラメータ
a = 1  # 波の高さ(振幅)
k = 2 * np.pi  # 周波数
omega = 2 * np.pi  # 角周波数
x = np.linspace(0, 10, 1000)  # x軸の範囲

# 波の式 (y = a * sin(kx - ωt) と仮定)
y = a * np.sin(k * x)

# プロット
plt.figure(figsize=(10, 4))
plt.plot(x, y, color="green")

# 軸のラベル
plt.xlabel("x")
plt.ylabel("Wave Height")

# B点のプロット
B_x = 0.4  # B点の位置 (例: x = 5)
B_y = a * np.sin(k * B_x)
plt.scatter(B_x, B_y, color="red")
plt.annotate("B", (B_x, B_y), textcoords="offset points", xytext=(0, 10), ha='center', color="red")


# 波の進む向きを矢印で示す
plt.arrow(2, 1.2, 2.5, 0, head_width=0.3, head_length=0.3, fc='black', ec='black')

# y軸の範囲を設定
plt.ylim(-a * 1.5, a * 1.5)

# グリッド表示
plt.grid(True)

# グラフを表示
plt.show()

オイラーの公式

下記のオイラーの公式をつかうことで三角関数は、虚数と指数関数をつかって表現できます。

$$e^{i\theta} = \cos\theta + i\sin\theta$$

• $e$ はネイピア数（自然対数の底、約2.718）。
• $i$ は虚数単位で、$i^2 = -1$ という性質を持っています。
• $\theta$ は角度を表します（通常ラジアン単位で）。

この公式は、複素数平面において、指数関数と三角関数の関係を示すものです。
この関係式により三角関数を極形式、指数関数としてあらわすことができるようになります。

https://manabitimes.jp/math/585

複素数の極形式の２つ表し方

複素数の表現方法として極形式というのものがあります。
高校で習うのは $z=a+bi$ という形でしたがこれを
複素数平面上で $z = r (\cos\theta + i \sin\theta)$ という形になおしたものが極形式1 です。さらに上記のオイラーの公式をつかい　$re^{i\theta}$ という形になおしたものが極形式2　です。（1や2は便宜上勝手につけただけで正式な呼び名では付きません)

例えば　

$$1+i$$

を複素数平面上で表すと下記のpythonで作成した図になりますが、
これを極形式1であらわすと

$$\sqrt{2}(\cos\frac{\pi}{4} + i \sin\frac{\pi}{4})$$

で表すことができます。

さらに極形式2 であらわすと下記になります。

$$\sqrt{2}e^{i\frac{\pi}{4}}$$

メリットはよく分からなくても、なんとなくスッキリして、かっこいいという感覚を持ちます。

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
r = np.sqrt(2)  # 絶対値
theta = np.pi / 4  # 角度 (例: 45度)

# 実部と虚部を計算
x = r * np.cos(theta)
y = r * np.sin(theta)

# 複素数平面の描画
plt.figure(figsize=(6, 6))
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)

# 複素数 z = r(cosθ + i sinθ) をプロット
plt.plot([0, x], [0, y], label=r'$re^{i\theta}$', color='green')
plt.scatter(x, y, color='green')

# 角度 θ の弧を描く
arc = np.linspace(0, theta, 100)
plt.plot(r * np.cos(arc), r * np.sin(arc), color='green', linestyle='dashed')

# 注釈
plt.text(x/2, y/2, r'$r$', fontsize=14, ha='center')
plt.text(x + 0.1, y, r'$r\cos\theta + i r\sin\theta$', fontsize=12, color='green')
plt.text(0.5, 0.2, r'$\theta$', fontsize=14)

# 軸ラベル
plt.xlabel('Re')
plt.ylabel('Im')

# グリッド表示
plt.grid(True)
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)

# 描画
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

https://manabitimes.jp/math/875

波を表すのに虚数を使うのはなぜ？

上記のオイラーの公式をつかうと、　指数関数( $e^{i\theta}$ )で波を表現できるようになりました。
指数関数として表現すると指数法則が適用でき掛け算が足し算に、　割り算が引き算とあつかえるので扱いやすいというメリットがあります。
https://manabitimes.jp/math/1535

例えば下記の複素数の掛け算を考えてみます。

$$(1+i)(\sqrt{3}+i)$$

極形式1 になおす

$$(\sqrt{2}(\cos\frac{\pi}{4} + i \sin\frac{\pi}{4}))(2(\cos\frac{\pi}{6} + i \sin\frac{\pi}{6}))$$

極形式2 になおす

$$\sqrt{2}e^{i\frac{\pi}{4}}2e^{i\frac{\pi}{6}}$$

指数法則を適用

$$2\sqrt{2}e^{i(\frac{\pi}{4}+\frac{\pi}{6})}$$

ここで、波を表すときに三角関数のままだと、極形式1のような計算になり、三角関数積和の公式など複雑な計算が必要です。
https://manabitimes.jp/math/660

それが極形式2 を使うことで単純な掛け算と、足し算でよくなりました。
このように、実用的な理由で波を虚数の指数関数として表すことが多いようです。

これらを可視化すると下記のようなプログラムになります。

# パラメータ設定
r1 = 2  # z1 の絶対値
r2 = np.sqrt(2)  # z2 の絶対値
theta1 = np.pi / 6  # z1 の角度 (30度)
theta2 = np.pi / 4  # z2 の角度 (45度)

# z1, z2, z1*z2 の実部と虚部を計算
x1, y1 = r1 * np.cos(theta1), r1 * np.sin(theta1)
x2, y2 = r2 * np.cos(theta2), r2 * np.sin(theta2)
x_product, y_product = r1 * r2 * np.cos(theta1 + theta2), r1 * r2 * np.sin(theta1 + theta2)

# 複素数平面の描画
plt.figure(figsize=(6, 6))
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)

# z1, z2, z1*z2 をプロット
plt.plot([0, x1], [0, y1], label=r'$z_1$', color='green')
plt.scatter(x1, y1, color='green')
plt.plot([0, x2], [0, y2], label=r'$z_2$', color='blue')
plt.scatter(x2, y2, color='blue')
plt.plot([0, x_product], [0, y_product], label=r'$z_1 \cdot z_2$', color='orange')
plt.scatter(x_product, y_product, color='orange')

# 角度の弧を描く
arc1 = np.linspace(0, theta1, 100)
arc2 = np.linspace(0, theta2, 100)
arc_product = np.linspace(0, theta1 + theta2, 100)
plt.plot(r1 * np.cos(arc1), r1 * np.sin(arc1), color='green', linestyle='dashed')
plt.plot(r2 * np.cos(arc2), r2 * np.sin(arc2), color='blue', linestyle='dashed')
plt.plot(r1 * r2 * np.cos(arc_product), r1 * r2 * np.sin(arc_product), color='orange', linestyle='dashed')

# 注釈
plt.text(x1/2, y1/3, r'$z_1$', fontsize=14, color='green')
plt.text(x2/2, y2/2, r'$z_2$', fontsize=14, color='blue')
plt.text(x_product/2, y_product/2, r'$z_1 \cdot z_2$', fontsize=14, color='orange')
plt.text(1.7, 0.1, r'$\theta_1$', fontsize=14, color='green')
plt.text(1.0, 0.7, r'$\theta_2$', fontsize=14, color='blue')
plt.text(1.8, 1.5, r'$\theta_1 + \theta_2$', fontsize=14, color='orange')

# 軸ラベル
plt.xlabel('Re')
plt.ylabel('Im')

# グリッド表示
plt.grid(True)
plt.xlim(-1, 3)
plt.ylim(-1, 3)

# 描画
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

フーリエ変換

さらに、　波を分析するうえで　欠かせないのがフーリエ変換です。

• フーリエ級数展開
  • 周期をもった複雑な波をどんな周期の波の成分がどれくらい含まれているか、フーリエ級数を展開して係数を調べることができる。

https://manabitimes.jp/math/1156

• 複素フーリエ級数
  • オイラーの公式から、フーリエ級数を指数関数であらわしたもの（三角関数より計算しやすい）

https://manabitimes.jp/math/1173

• フーリエ変換
  • 周期をもっていないものを無限大の周期としてあつかうことでフーリエ展開できるようにした

https://manabitimes.jp/math/2280

大事なこととして下記の関係を覚えておけばよいです。

• フーリエ変換：複雑な波から周波数ごとの波の要素に分解する
• 逆フーリエ変換：一つ一つシンプルな波を組み合わせて複雑な波を合成する

ならったことをプログラムにすると理解も進みます。

1. sin, cos それぞれ周波数の違う波を合成しW1を作成します
2. W1をフーリエ変換して周波数成分を分解します
3. ２の結果を逆フーリエ変換します

波をプログラムで制御できそうな気がしてきました。

import numpy as np
import matplotlib.pyplot as plt

# サンプリングパラメータ
sampling_rate = 1000  # サンプリング周波数（Hz）
T = 1.0 / sampling_rate  # サンプリング間隔
x = np.linspace(0.0, 1.0, sampling_rate, endpoint=False)  # 時間軸

# 異なる周波数のsin波とcos波を作成
freq1 = 5    # 5 Hzのsin波
freq2 = 50   # 50 Hzのsin波
freq3 = 120  # 120 Hzのsin波
freq4 = 30   # 30 Hzのcos波
freq5 = 90   # 90 Hzのcos波

# 各波の生成 (sin波とcos波)
wave1 = np.sin(2 * np.pi * freq1 * x)
wave2 = 0.5 * np.sin(2 * np.pi * freq2 * x)
wave3 = 0.2 * np.sin(2 * np.pi * freq3 * x)
wave4 = 0.3 * np.cos(2 * np.pi * freq4 * x)
wave5 = 0.1 * np.cos(2 * np.pi * freq5 * x)

# 合成波 W1 (sinとcosの波を合成)
W1 = wave1 + wave2 + wave3 + wave4 + wave5

# 1. 複数周期の違う波それぞれと、それを合成した波
plt.figure(figsize=(12, 8))
plt.subplot(4, 1, 1)
plt.plot(x, wave1, label="5 Hz sin Wave")
plt.plot(x, wave2, label="50 Hz sin Wave")
plt.plot(x, wave3, label="120 Hz sin Wave")
plt.plot(x, wave4, label="30 Hz cos Wave", linestyle='dashed')
plt.plot(x, wave5, label="90 Hz cos Wave", linestyle='dashed')
plt.title("Individual Waves")
plt.legend()

plt.subplot(4, 1, 2)
plt.plot(x, W1, label="Combined Wave (W1)")
plt.title("Combined Wave (W1) - sin and cos")
plt.legend()

# 2. W1 をフーリエ変換した結果
W1_fft = np.fft.fft(W1)
frequencies = np.fft.fftfreq(sampling_rate, T)
print(W1_fft)

plt.subplot(4, 1, 3)
plt.plot(frequencies[:sampling_rate // 2], np.abs(W1_fft)[:sampling_rate // 2])
plt.title("Fourier Transform of W1")
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')

plt.tight_layout()
plt.show()

# 3. 逆フーリエ変換結果
W1_ifft = np.fft.ifft(W1_fft)

plt.figure(figsize=(12, 4))
plt.plot(x, W1_ifft.real, label="Inverse Fourier Transform of W1")
plt.title("Inverse Fourier Transform Result")
plt.legend()
plt.show()

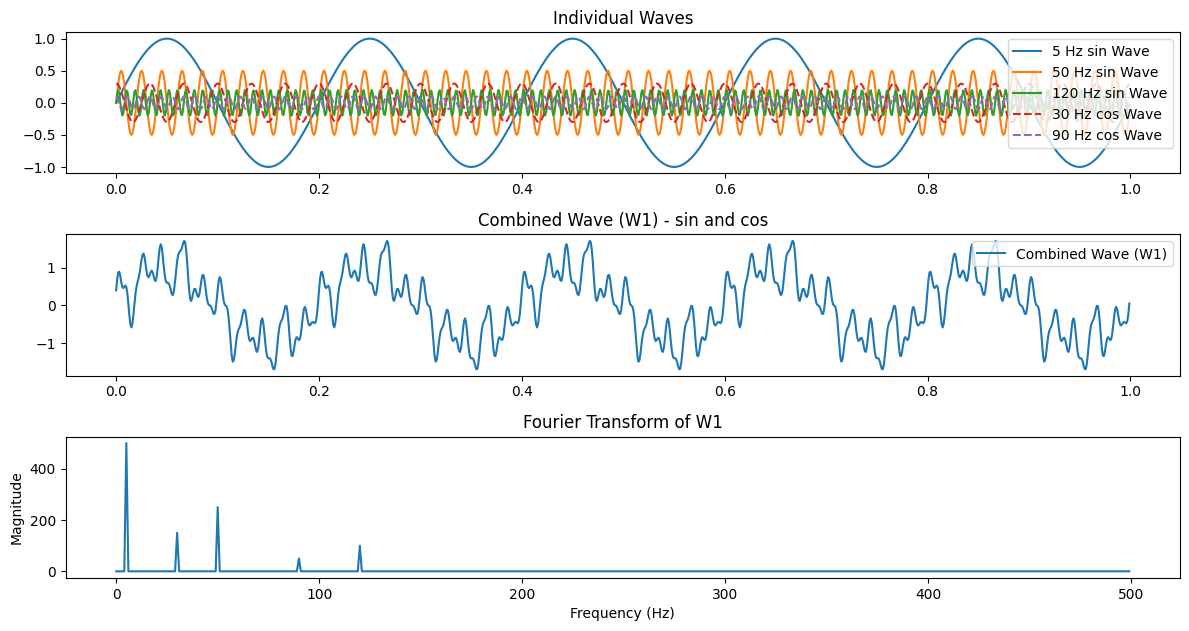
虚数、複素数をつかうことで　実数であらわすと2つの式になるものを1つの式で表現できるようになります。　フーリエ変換の場合は　Y軸に対して対称（偶関数）であるCos関数と、原点に対して対称（奇関数）であるSin関数　それぞれ実部と虚部にあらわすことで　一つの式で波の性質を表すことができるようになったということです。　　このときの虚数はもともとの意味、定義としてではなく、便利な道具として使われている。　そう使えるように新たな意味を定義したと捉えるのがよいようです。

この世界を、波を、数式で表せるように考えた先人、その考えに乗っかり、拡張して、電気、マイクロ波、通信、音波をつかった機械、衛星は動いていることが垣間見えました。