二重倒立振子における制御アルゴリズムの比較
はじめに
本記事では、物理システムのモデリングをしてシミュレーターの実装を行い、いくつかの主要な制御アルゴリズムを試します。制御応答のグラフを見るだけでなく、実際に物理シミュレーターに制御アルゴリズムを適用する制御工学の一連の流れを体験することで、実践的な基礎知識と各制御手法に対する肌感を身につけることを目的とします。
今回は制御器の性能をより分かりやすく見るために、不安定系であり、それなりに制御の難しい、1軸トルク入力の二重倒立振子を対象にしました。
また、本記事で実装されたコードは以下のリポジトリで公開しています。
ここで不安定系・安定系とは以下を意味しています。
- 不安定系: 二重倒立振子のように、制御入力がない場合に自然に平衡点から離れてしまい、転倒してしまう系を不安定系と呼ばれます。このようなシステムは、常に制御入力を適切に調整することでのみ、特定の状態(例えば、上向きに立っている状態)を維持することができます。制御入力がなければ、システムは元の状態から大きく離れてしまいます。
- 安定系: 自動運転の経路追従問題のように、制御入力を止めた場合にシステムがその場で停止し、誤差がそれ以上大きくならない場合、この系は「安定系」と呼ばれます。具体的には、システムが元の位置から大きくずれることなく、状態が一定の範囲内に収まるようなシステムを安定系と言います。経路追従の文脈では、車両が制御なしで停車し続ける場合、システムが安定していると考えられます。
物理システムのモデリング
物理システム全般的に、解析力学のラグランジュの運動方程式を用いてモデリングすることがメジャーな方法一つです。運動エネルギーとポテンシャルエネルギーから運動方程式を導くことができます。モデルの導出の部分は他の記事では省略されて始まることが多いですが、自分で好きなモデルに適用できるうように、本記事ではモデリングの手順を示します。
求めたい形は、モデルの状態量をx、制御入力をuとして、高次の微分を低次の微分で表すような以下の形です。
ここで状態量とは、一軸トルク制御の二重倒立振子であれば
シミュレーター側には制御入力を与えた時にの挙動を再現するために必ずモデルが必要になります。
一方で制御側にはその手法とシミュレーション条件によっても変わってきます。
例えばPID制御はモデルを必要としない手法であり、観測値と目標値の差を元にフィードバック制御を行います。MPCの場合はモデルを使った将来挙動の予測に基づき最適な制御入力を求めます。LQRは線形システムに対して最適な制御入力を求める手法であり、システムの線形な状態空間モデルが必要になります。
シミュレーター側のモデルを既知として全く同じモデル・限りなく近いモデルを使うのは実世界の制御を考えると反則ですが、本記事では基本は既知として進めます。物理システムのモデルを知ることが出来ない場合は、入力や測定値からそのモデルを推定するようなシステム同定が必要になります。
参考記事
以下の記事が参考になりました。車輪型と台車型の倒立振子を例として、運動方程式を立てて、SymPyを使って偏微分をしながら、シミュレーション出来る形に落とし込んでいきます。SymPyはシンボリック表現を使って方程式を定義して、解析解を求めることができるPythonのライブラリです。
また、LQRのような線形制御を使う場合は、モデルの線形化が必要になり、この際にもSymPyを使って平衡点の周りで線形化を行い、その時の状態空間モデルの行列を求めることができます。
二重倒立振子のモデリング
制御工学を扱う上で教科書的な題材であるため、検索するとGitHubのコードや記事等に色んな式が出てきます。しかし、統一的なモデリングがあまり無さそうで、簡略されたものや、摩擦がなかったり、慣性モーメントが考慮できてなかったりするものが多いです。間違っていそうな式も多くあるように感じました。
シンプルな二重倒立振子
まずは、雰囲気を掴むために、簡略化されたモデルの例から見ていきましょう。こちらのPDFが参考になりました。
リンク自体には質量がなく、ジョイント部分のみに質量があるという簡略化されたモデルが書かれています。制御入力は今回は考えません。
このモデルは、ラグランジュの運動方程式を使って以下のような式を導出することができます。
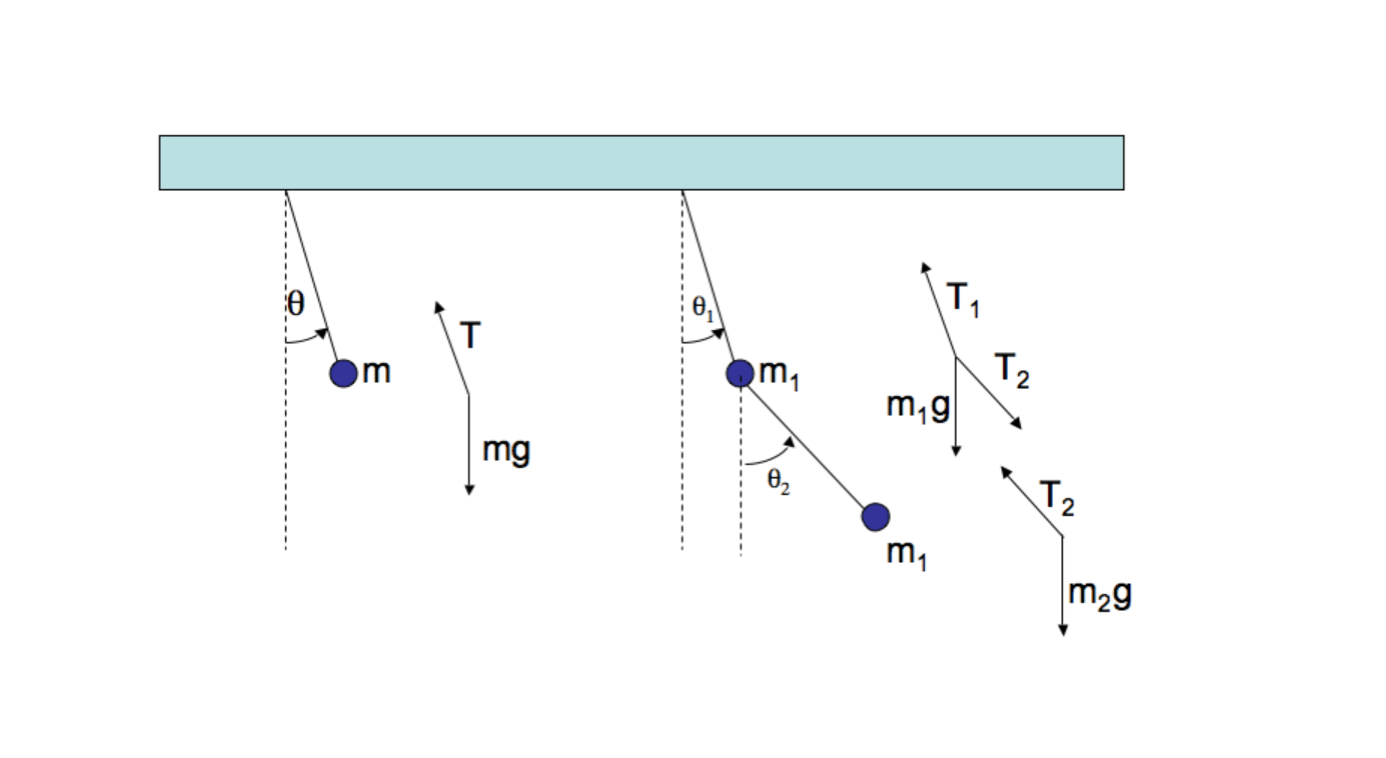
まずは、この連立方程式を
import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, init_vprinting
init_vprinting()
theta1, theta2 = dynamicsymbols('theta1 theta2') # 角度
theta1_dot, theta2_dot = dynamicsymbols('theta1 theta2', 1) # 角速度
theta1_ddot, theta2_ddot = dynamicsymbols('theta1 theta2', 2) # 角加速度
m1, m2, L1, L2, g = sp.symbols('m1 m2 L1 L2 g') # 質量、棒の長さ、重力加速度
# 方程式
eq1 = (m1 + m2) * L1 * theta1_ddot + m2 * L2 * theta2_ddot * sp.cos(theta1 - theta2) + m2 * L2 * theta2_dot**2 * sp.sin(theta1 - theta2) + g * (m1 + m2) * sp.sin(theta1)
eq2 = m2 * L2 * theta2_ddot + m2 * L1 * theta1_ddot * sp.cos(theta1 - theta2) - m2 * L1 * theta1_dot**2 * sp.sin(theta1 - theta2) + g * m2 * sp.sin(theta2)
# 連立方程式を解く
solutions = sp.solve([eq1, eq2], (theta1_ddot, theta2_ddot))
display(sp.simplify(solutions[theta1_ddot]))
display(sp.simplify(solutions[theta2_ddot]))
Output:
シンプルなモデルですが、意外と複雑な式になります。これで以下の形式で表すことができました。
倒立振子は真上の平衡状態を目標状態としたいので、上を
import sympy as sp
from sympy.physics.mechanics import dynamicsymbols
t = sp.symbols('t')
theta1 = dynamicsymbols('theta1')
theta2 = dynamicsymbols('theta2')
theta1 = theta1
theta2 = theta2
l1, l2, m1, m2, g = sp.symbols('L1 L2 m1 m2 g')
x1 = l1 * sp.sin(theta1)
y1 = l1 * sp.cos(theta1)
x2 = l1 * sp.sin(theta1) + l2 * sp.sin(theta2)
y2 = l1 * sp.cos(theta1) + l2 * sp.cos(theta2)
T1 = m1 * (sp.diff(x1, t)**2 + sp.diff(y1, t)**2) / 2
T2 = m2 * (sp.diff(x2, t)**2 + sp.diff(y2, t)**2) / 2
T = T1 + T2
V1 = m1 * g * y1
V2 = m2 * g * y2
V = V1 + V2
L = T - V
lagrange_eq1 = sp.diff(sp.diff(L, sp.diff(theta1, t)), t) - sp.diff(L, theta1)
tau = sp.symbols('tau')
lagrange_eq1 = lagrange_eq1 - tau
lagrange_eq2 = sp.diff(sp.diff(L, sp.diff(theta2, t)), t) - sp.diff(L, theta2)
solutions = sp.solve([lagrange_eq1, lagrange_eq2], [theta1.diff(t, 2), theta2.diff(t, 2)])
F_theta1_ddot = solutions[theta1.diff(t, 2)]
F_theta2_ddot = solutions[theta2.diff(t, 2)]
display(F_theta1_ddot.simplify())
display(F_theta2_ddot.simplify())
Output:
次に、
A10 = F_theta1_ddot.diff(theta1).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
A11 = F_theta1_ddot.diff(theta1.diff(t)).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
A12 = F_theta1_ddot.diff(theta2).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
A13 = F_theta1_ddot.diff(theta2.diff(t)).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
A30 = F_theta2_ddot.diff(theta1).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
A31 = F_theta2_ddot.diff(theta1.diff(t)).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
A32 = F_theta2_ddot.diff(theta2).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
A33 = F_theta2_ddot.diff(theta2.diff(t)).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
B00 = F_theta1_ddot.diff(tau).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
B30 = F_theta2_ddot.diff(tau).subs([(theta1, 0), (theta2, 0), (theta1.diff(t), 0), (theta2.diff(t), 0)])
display(A10.simplify())
display(A11.simplify())
display(A12.simplify())
display(A13.simplify())
display(A30.simplify())
display(A31.simplify())
display(A32.simplify())
display(A33.simplify())
display(B00.simplify())
display(B30.simplify())
Output:
この線形化された状態空間モデルは、LQRのような線形制御を用いる場合に使うことができます。
リンク質量や摩擦を考慮した二重倒立振子
今度は、リンク自体に質量を持たせたり、摩擦考慮したり、もう少し複雑なモデルを考えます。
倒立振子で学ぶ制御工学 を引用して、リンク質量や粘性摩擦を考慮した二重倒立振子において、ラグランジュの運動方程式より導出した(3.54) (3.55)式を参考に、さらに動摩擦を考慮したモデルを考えます。動摩擦により非連続な式になり、微分情報が使えなくなるなど、制御が難しくなります。
まずは、連立運動方程式をsympyで定義します。
# 倒立振子で学ぶ制御工学 (3.54) (3.55) に摩擦を追加する
import sympy as sp
import sys
sys.setrecursionlimit(1500)
# 時間変数の定義
t = sp.symbols("t")
# 角度とその時間微分の定義
theta1 = sp.Function("theta1")(t)
theta2 = sp.Function("theta2")(t)
theta1_dot = sp.diff(theta1, t)
theta2_dot = sp.diff(theta2, t)
theta1_ddot = sp.diff(theta1, t, t)
theta2_ddot = sp.diff(theta2, t, t)
# 定数の定義
alpha1, alpha2, alpha3, alpha4, alpha5, mu1, mu2, tau1, f1, f2 = sp.symbols(
"alpha1 alpha2 alpha3 alpha4 alpha5 mu1 mu2 tau1 f1 f2"
)
theta12 = theta1 - theta2
# 連立方程式の定義
eq1 = sp.Eq(
alpha1 * theta1_ddot + alpha3 * sp.cos(theta12) * theta2_ddot,
-alpha3 * theta2_dot**2 * sp.sin(theta12)
+ alpha4 * sp.sin(theta1)
- (mu1 + mu2) * theta1_dot
+ mu2 * theta2_dot
+ tau1
- sp.sign(theta1_dot) * f1,
)
eq2 = sp.Eq(
alpha3 * sp.cos(theta12) * theta1_ddot + alpha2 * theta2_ddot,
alpha3 * theta1_dot**2 * sp.sin(theta12)
+ alpha5 * sp.sin(theta2)
+ mu2 * theta1_dot
- mu2 * theta2_dot
- sp.sign(theta2_dot - theta1_dot) * f2,
)
display(eq1.simplify())
display(eq2.simplify())
Output:
ここで、
連立方程式を解いて、
# 連立方程式の解を求める
solutions = sp.solve([eq1, eq2], (theta1_ddot, theta2_ddot))
theta1_ddot_sol = solutions[theta1_ddot]
theta2_ddot_sol = solutions[theta2_ddot]
display(theta1_ddot_sol)
display(theta2_ddot_sol)
Output:
長い。。!そしてSymPy凄いです。
これを
動摩擦のsignの非連続の項を抜いた上でもう一度解を求め、線形化を行います。
A10 = theta1_ddot_sol.diff(theta1).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
A11 = theta1_ddot_sol.diff(theta1_dot).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
A12 = theta1_ddot_sol.diff(theta2).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
A13 = theta1_ddot_sol.diff(theta2_dot).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
A30 = theta2_ddot_sol.diff(theta1).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
A31 = theta2_ddot_sol.diff(theta1_dot).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
A32 = theta2_ddot_sol.diff(theta2).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
A33 = theta2_ddot_sol.diff(theta2_dot).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
B00 = theta1_ddot_sol.diff(tau1).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
B30 = theta2_ddot_sol.diff(tau1).subs([(theta1, 0), (theta2, 0), (theta1_dot, 0), (theta2_dot, 0)])
display(A10.simplify())
display(A11.simplify())
display(A12.simplify())
display(A13.simplify())
display(A30.simplify())
display(A31.simplify())
display(A32.simplify())
display(A33.simplify())
display(B00.simplify())
display(B30.simplify())
Output:
今度は線形化が成功しました。これで線形化した状態空間モデルが求められました。
これらの計算を結果をもとに、以下のようにDynamicsクラスを作成しました。非線形なダイナミクスと線形なダイナミクスどちらも含んでいます。
import numpy as np
from dynamics.base import Dynamics
from utils.math import sign
G = 9.8 # acceleration due to gravity, in m/s^2
class DoubleInvertedPendulumDynamics(Dynamics):
def __init__(
self, L1, L2, l1, l2, M1, M2, I1, I2, c1, c2, f1, f2, use_linearlized_dynamics
):
self.L1 = L1
self.L2 = L2
self.l1 = l1
self.l2 = l2
self.M1 = M1
self.M2 = M2
self.I1 = I1
self.I2 = I2
self.c1 = c1
self.c2 = c2
self.f1 = f1
self.f2 = f2
self.alpha1 = I1 + M1 * l1**2 + M2 * L1**2
self.alpha2 = I2 + M2 * l2**2
self.alpha3 = M2 * L1 * l2
self.alpha4 = (M1 * l1 + M2 * L1) * G
self.alpha5 = M2 * l2 * G
self.params = np.array(
[
self.alpha1,
self.alpha2,
self.alpha3,
self.alpha4,
self.alpha5,
f1,
f2,
c1,
c2,
]
)
self.use_linearlized_dynamics = use_linearlized_dynamics
self.A, self.B, self.C, self.D = self.create_state_space()
def create_state_space(self):
denominator = self.alpha1 * self.alpha2 - self.alpha3**2
A10 = self.alpha2 * self.alpha4 / denominator
A11 = (
-(self.alpha2 * self.c1 + self.alpha2 * self.c2 + self.alpha3 * self.c2)
/ denominator
)
A12 = -self.alpha3 * self.alpha5 / denominator
A13 = self.c2 * (self.alpha2 + self.alpha3) / denominator
A30 = -self.alpha3 * self.alpha4 / denominator
A31 = (
self.alpha1 * self.c2 + self.alpha3 * self.c1 + self.alpha3 * self.c2
) / denominator
A32 = self.alpha1 * self.alpha5 / denominator
A33 = -self.c2 * (self.alpha1 + self.alpha3) / denominator
B00 = self.alpha2 / denominator
B30 = -self.alpha3 / denominator
A = np.zeros((4, 4))
A[0, 1] = 1
A[2, 3] = 1
A[1, 0] = A10
A[1, 1] = A11
A[1, 2] = A12
A[1, 3] = A13
A[3, 0] = A30
A[3, 1] = A31
A[3, 2] = A32
A[3, 3] = A33
B = np.zeros((4, 1))
B[1, 0] = B00
B[3, 0] = B30
C = np.eye(4)
D = np.zeros((4, 1))
return A, B, C, D
def update_state(self, state, t, u):
return (
self.update_state_with_liniarized_dynamics(state, t, u)
if self.use_linearlized_dynamics
else self.update_state_with_nonlinear_dynamics(state, t, u)
)
def update_state_with_liniarized_dynamics(self, state, t, u):
state_dot = self.A @ state + self.B @ u
return state_dot
def update_state_with_nonlinear_dynamics(self, state, t, u):
# 倒立振子で学ぶ制御工学 (3.54) (3.55) に摩擦を追加する
theta1, theta1_dot, theta2, theta2_dot = state
theta12 = theta1 - theta2
cos_theta12 = np.cos(theta12)
sin_theta12 = np.sin(theta12)
denominator = self.alpha1 * self.alpha2 - self.alpha3**2 * cos_theta12**2
theta1_ddot = (
-self.alpha2 * self.alpha3 * sin_theta12 * theta2_dot**2
+ self.alpha2 * self.alpha4 * np.sin(theta1)
- self.alpha2 * self.f1 * sign(theta1_dot)
- self.alpha2 * self.c1 * theta1_dot
- self.alpha2 * self.c2 * theta1_dot
+ self.alpha2 * self.c2 * theta2_dot
+ self.alpha2 * u
- self.alpha3**2 * sin_theta12 * cos_theta12 * theta1_dot**2
- self.alpha3 * self.alpha5 * np.sin(theta2) * cos_theta12
+ self.alpha3 * self.f2 * sign(-theta1_dot + theta2_dot)
- self.alpha3 * self.c2 * cos_theta12 * theta1_dot
+ self.alpha3 * self.c2 * cos_theta12 * theta2_dot
) / denominator
theta2_ddot = (
self.alpha1 * self.alpha3 * sin_theta12 * theta1_dot**2
+ self.alpha1 * self.alpha5 * np.sin(theta2)
- self.alpha1 * self.f2 * sign(-theta1_dot + theta2_dot)
+ self.alpha1 * self.c2 * theta1_dot
- self.alpha1 * self.c2 * theta2_dot
+ self.alpha3**2 * sin_theta12 * cos_theta12 * theta2_dot**2
- self.alpha3 * self.alpha4 * np.sin(theta1) * cos_theta12
+ self.alpha3 * self.f1 * sign(theta1_dot)
+ self.alpha3 * self.c1 * cos_theta12 * theta1_dot
+ self.alpha3 * self.c2 * cos_theta12 * theta1_dot
- self.alpha3 * self.c2 * cos_theta12 * theta2_dot
- self.alpha3 * u * cos_theta12
) / denominator
dxdt = np.zeros_like(state)
dxdt[0] = theta1_dot
dxdt[1] = theta1_ddot
dxdt[2] = theta2_dot
dxdt[3] = theta2_ddot
return dxdt
あとはSimulatorクラスを作成して、先ほどのDynamicsを渡した上で、数値積分を行って微小時間ごとに状態を更新していきます。数値積分の方法にはシンプルなものではオイラー法があり、より精度の高くて良く使われるものにルンゲクッタ法があります。
また、シミュレーターには以下のような機能も追加しました。
- 観測ノイズの追加
- 観測値の量子化
- 制御器周期とSimulation周期のずれ
- 制御入力遅延
制御器の実装・検証
先ほどの二重倒立振子シミュレーターに任意の初期状態を与えて、目標状態(上に立っている状態
初期状態は

また、シミュレーション時間は10秒間として、その間に
またAverage Proccesing Timeは、10s間のシミュレーションにおいて、制御計算時間含めて全体にかかった時間の各試行における平均を示します。ここで制御単体の時間ではなくて、シミュレーションの時間も含んでおりますが、制御器同士の相対的な処理時間の比較には有用な値です。また、マルチプロセスで各試行を並列で計算しているためCPU負荷率は高く、各プロセスひとつずつの処理時間は通常よりも長くなっております。
※以降の検証において、各制御アルゴリズムの実装は簡易的なものであり、その性能を最大限に発揮出来ているものではありません(ロジック改善、パラメタ調整、ソルバーの選定等)。あくまでサクッと実装したものに対して、どのくらいの性能が出るかを大まかに見るため記載ものになります。処理時間に関しても、高速化の余地は大いに残っています。
PID
世の中の9割の制御はPID制御(比例・積分・微分制御、Proportional-Integral-Derivative Control)が使われているとも言われるくらいもっともメジャーな手法です。例えば、自動運転OSSのAutowareの速度制御はPID制御を使っています。
PID制御は、制御対象の状態を目的の状態に近づけるために、現在の誤差(目的とする値と実際の値の差)を使って出力を調整します。
比例制御は、誤差に比例した制御出力を生成します。比例ゲイン
ここで、
積分制御は、誤差の過去の積分を考慮します。これは、システムが目標に到達するのに時間がかかり、定常の誤差が残る場合でも、最終的に目標に到達することを保証します。積分ゲイン
微分制御は、誤差の変化率を考慮します。これは、システムが急速に変化する場合に、過剰な調整を防ぐのに役立ちます。システムの応答を滑らかにし、オーバーシュートを減らすのに有効です。微分ゲイン ( K_d ) を設定し、制御出力は次のように計算されます。
PID制御器の出力は、比例、積分、微分の各成分を合計したものとなります。
この式を使って、制御システムは動作します。各ゲインK_p, K_i, K_dは、システムの応答を調整するために調整されます。
シンプルな実装は以下の通りです。
import numpy as np
from controller.base import Controller
from utils.math import sign
class PIDController(Controller):
def __init__(self, Kp, Ki, Kd, dt):
super().__init__(dt)
self.Kp = Kp
self.Ki = Ki
self.Kd = Kd
self.integral = 0.0
self.previous_error = 0.0
def control(self, state, desired_state, t):
if (
self.last_update_time is None
or np.round(t - self.last_update_time, 2) >= self.dt
):
self.last_update_time = t
error = desired_state - state
self.integral += error * self.dt
derivative = (error - self.previous_error) / self.dt
self.u = np.array(
[
np.dot(self.Kp, error)
+ np.dot(self.Ki, self.integral)
+ np.dot(self.Kd, derivative)
]
)
self.previous_error = error
ここで、ベースクラスのControllerはSimulatorとのインターフェイスを揃えるためのものです。
動摩擦や観測値の量子化やノイズ付与も無しの二重倒立振子シミュレーターに適用してみます。
ゲインの調整を色々したのですが、斜めった状態から立たすことどころか、
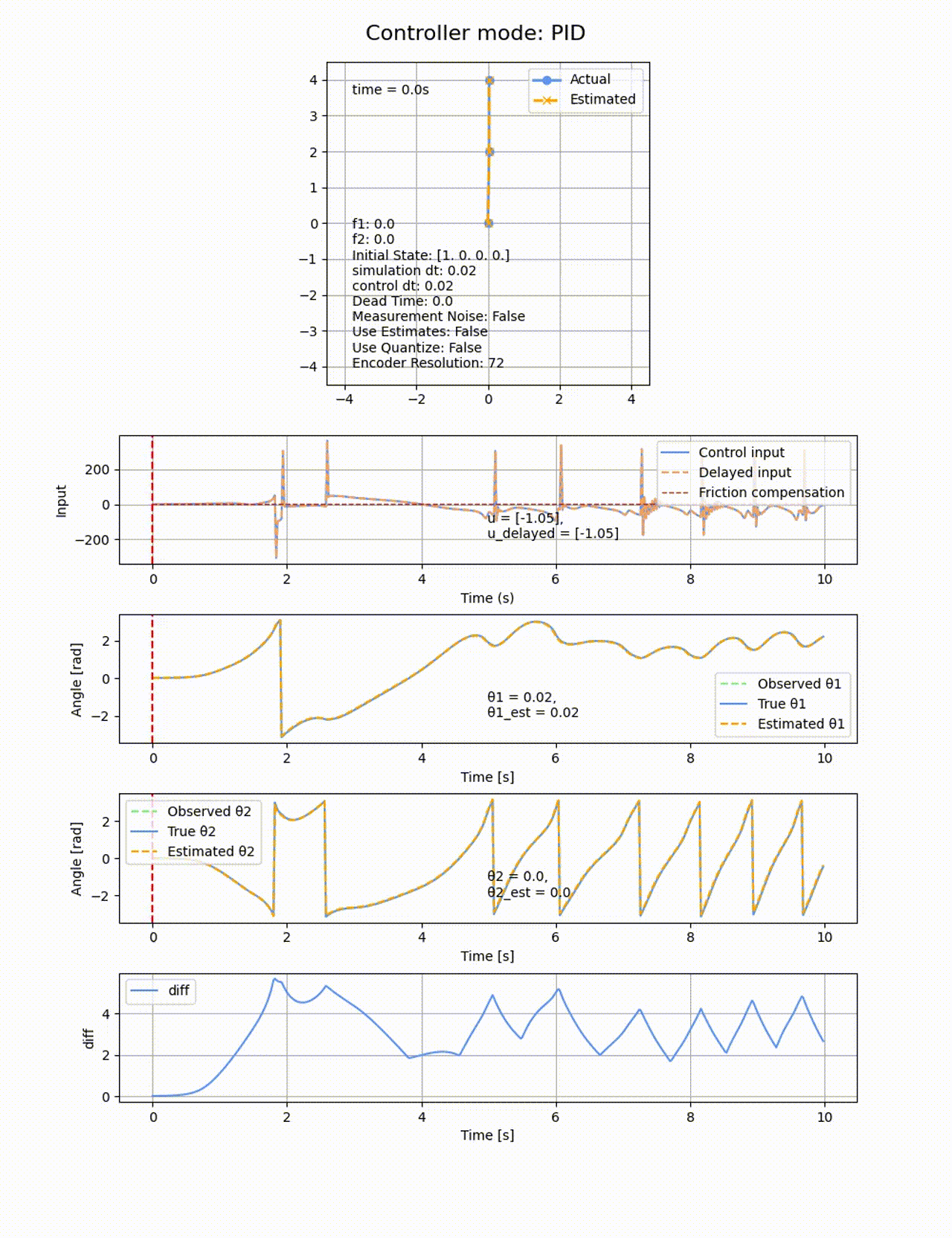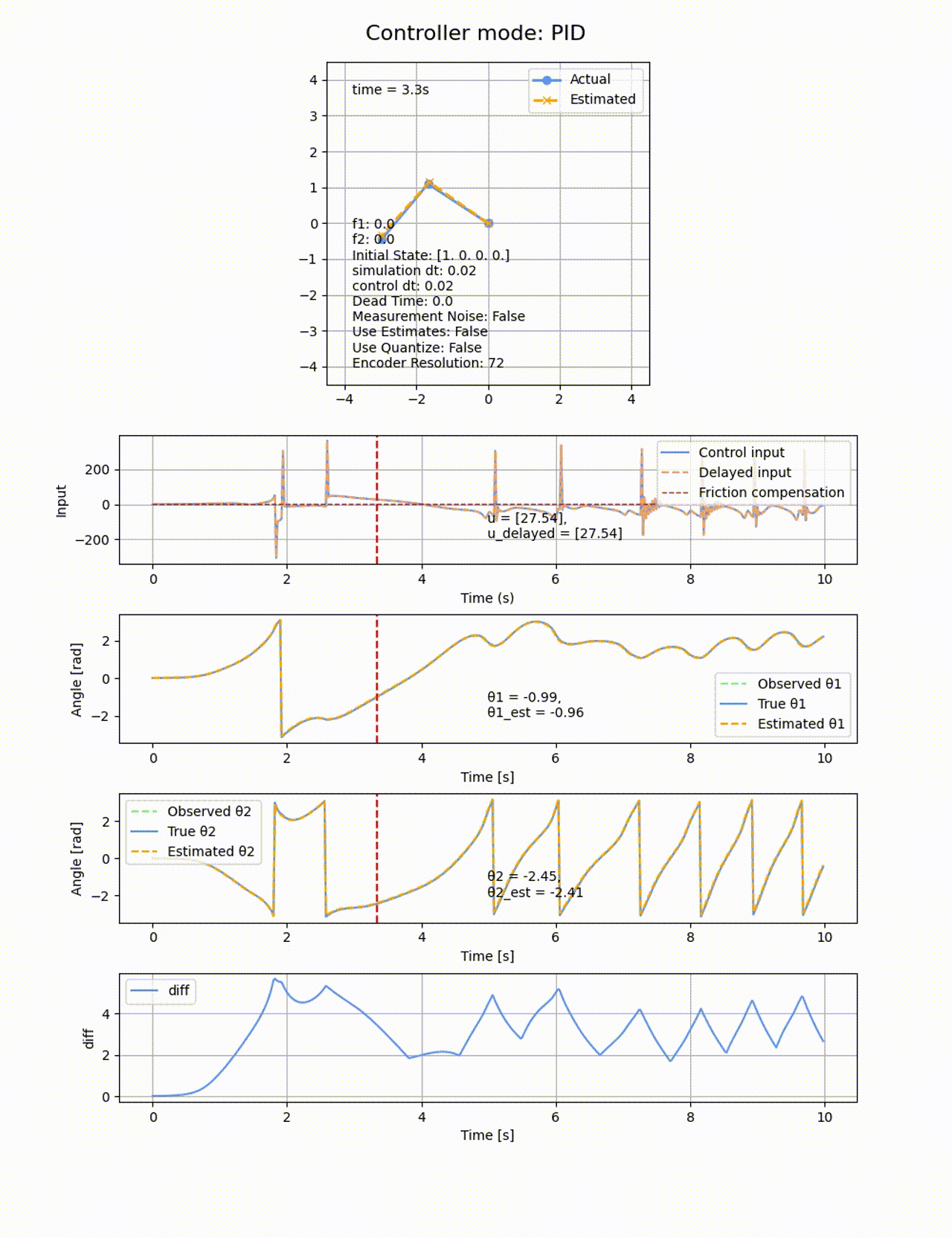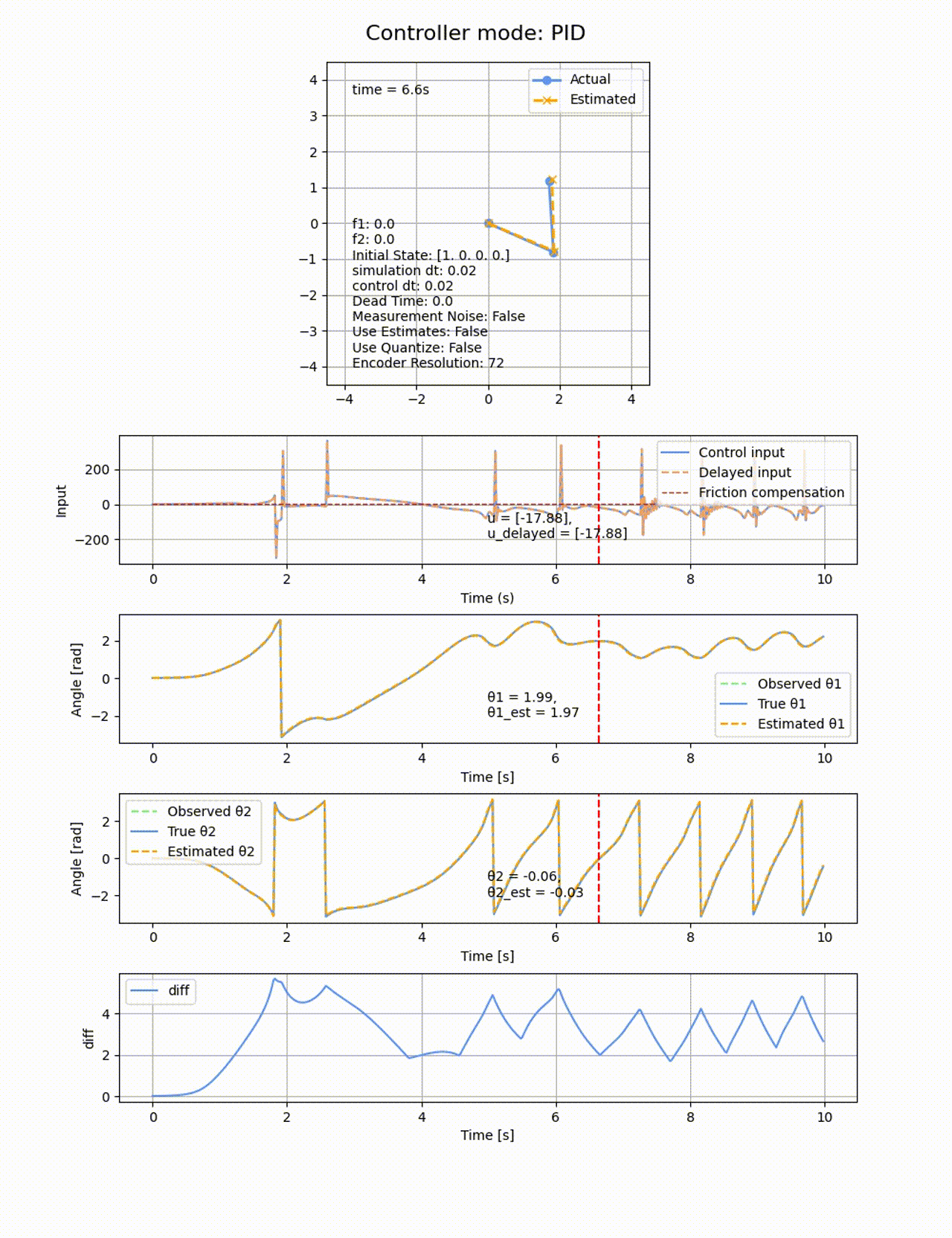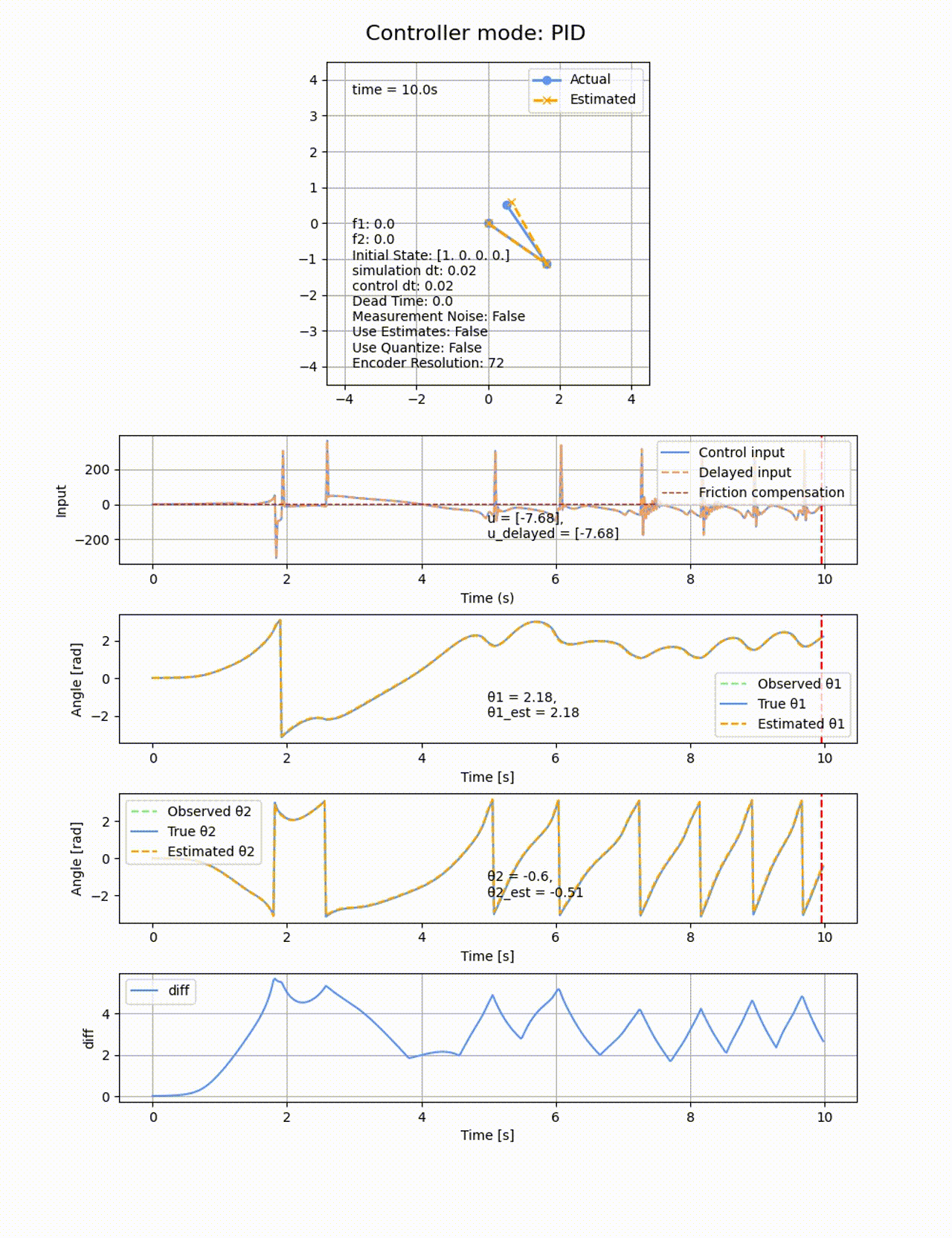
今回の系はSIMO (Single Input Multiple Output)と呼ばれる、1つの入力(トルク)が複数の出力(
PID制御におけるROAを求めます。初期値は

極配置
極配置法は、システムの動特性を望ましいものにするために、閉ループシステムの固有値(極)を任意の位置に配置する方法です。極の配置を適切に選ぶことで、システムの応答速度や安定性を調整することができます。状態フィードバックゲインKを設計して、閉ループシステムの固有値を希望する位置に配置することを目指します。
この時の制御入力uは

実装は以下の通りです。
import numpy as np
import control
from scipy.signal import place_poles
from controller.base import Controller
from utils.math import sign
class PolePlacementController(Controller):
def __init__(self, A, B, desired_poles, dt):
super().__init__(dt)
self.K = self._calculate_pole_placement_gain(A, B, desired_poles)
def _calculate_pole_placement_gain(self, A, B, desired_poles):
K = control.place(A, B, desired_poles)
return K
def control(self, state, desired_state, t):
if (
self.last_update_time is None
or np.round(t - self.last_update_time, 2) >= self.dt
):
self.last_update_time = t
self.u = -self.K @ (state - desired_state)
return self.u
python-controlのplace関数を使うと、一行で極配置をして状態フィードバックゲインを求めてくれます。
K = control.place(A, B, desired_poles)
scipy.signal.place_poles()という関数もありますが、python-controlのものはこの関数をラップしているものになります。scipyを直接使うと色んなアルゴリズムが選択できますが、python-controlのデフォルトのTits and Yangアルゴリズムを今回は使いました。
システムの動特性を望ましいものにするために、極を選択する必要がありますが、これが難しいです。一般的には、重根を避ける方がシステムのロバスト性と応答特性が向上するため、重根を持たない設計が推奨されることが多いです。極の大きさは、システムの固有振動数や希望する応答時間に基づいて選択します。極の実部は固有周波数の数倍に設定する等の決め方があります。数倍と言われても広すぎて良くわからないので、実際には適当に調整して挙動を見ながら決めていきます。
今回は、極は[-1, -2, -3, -4]として、初期値
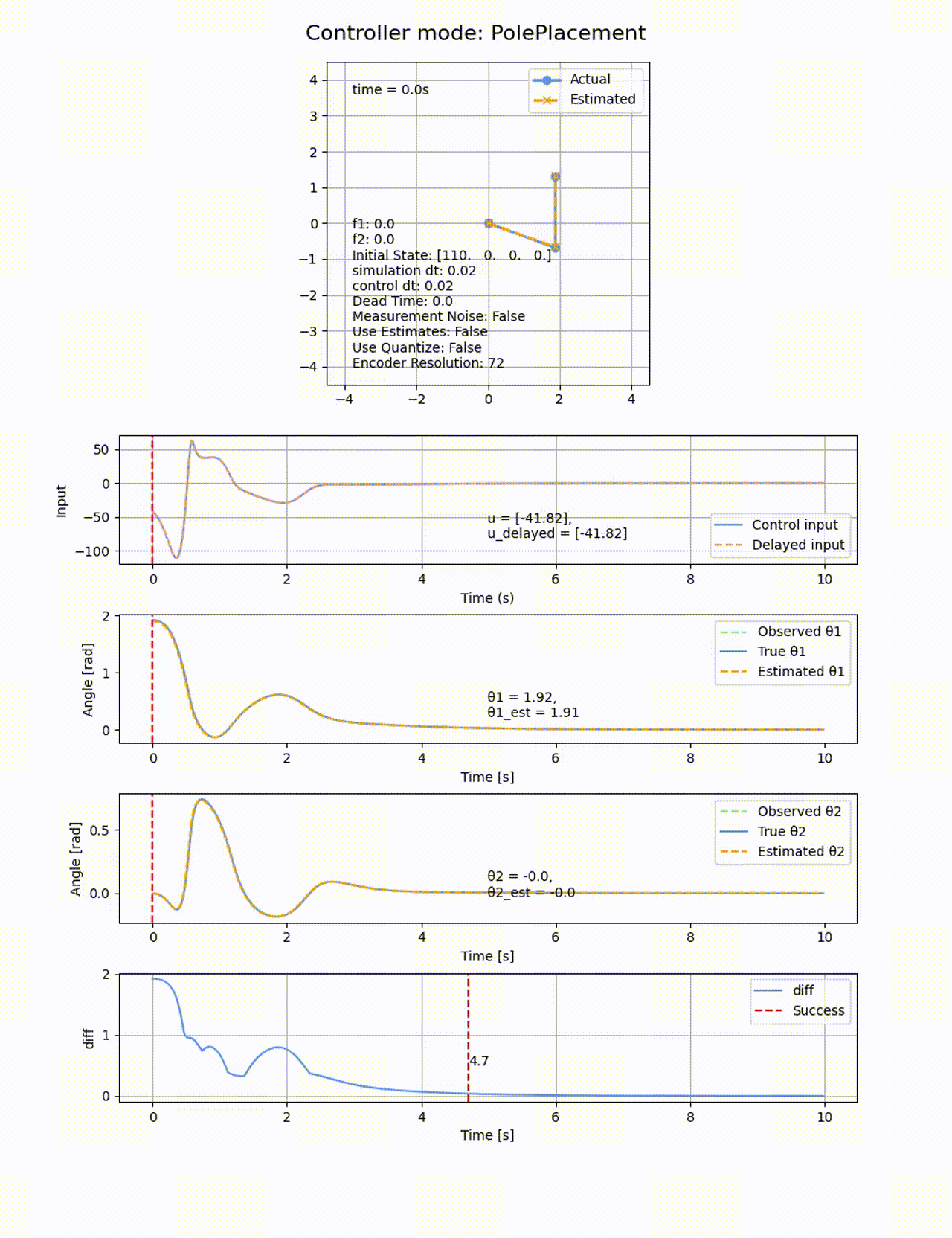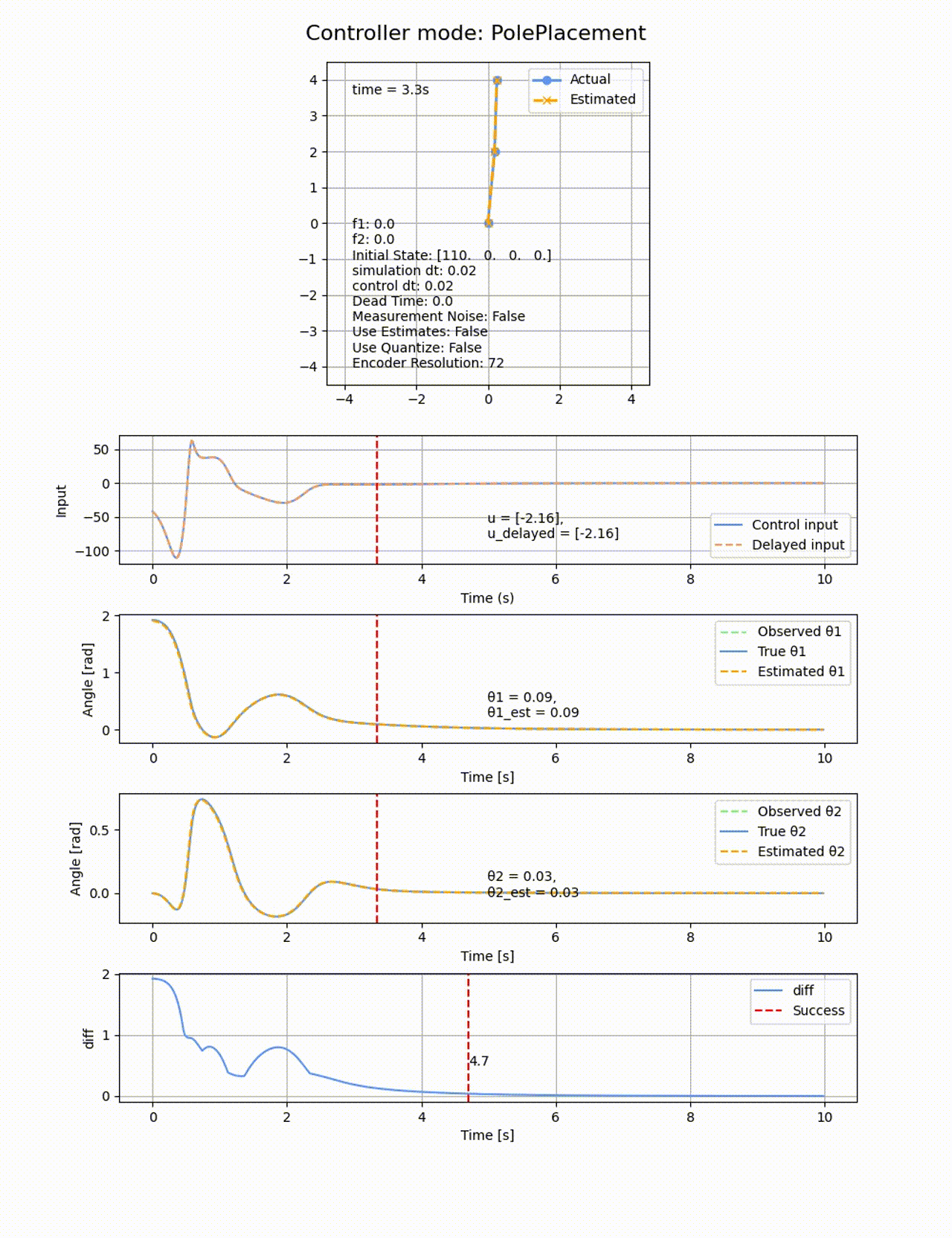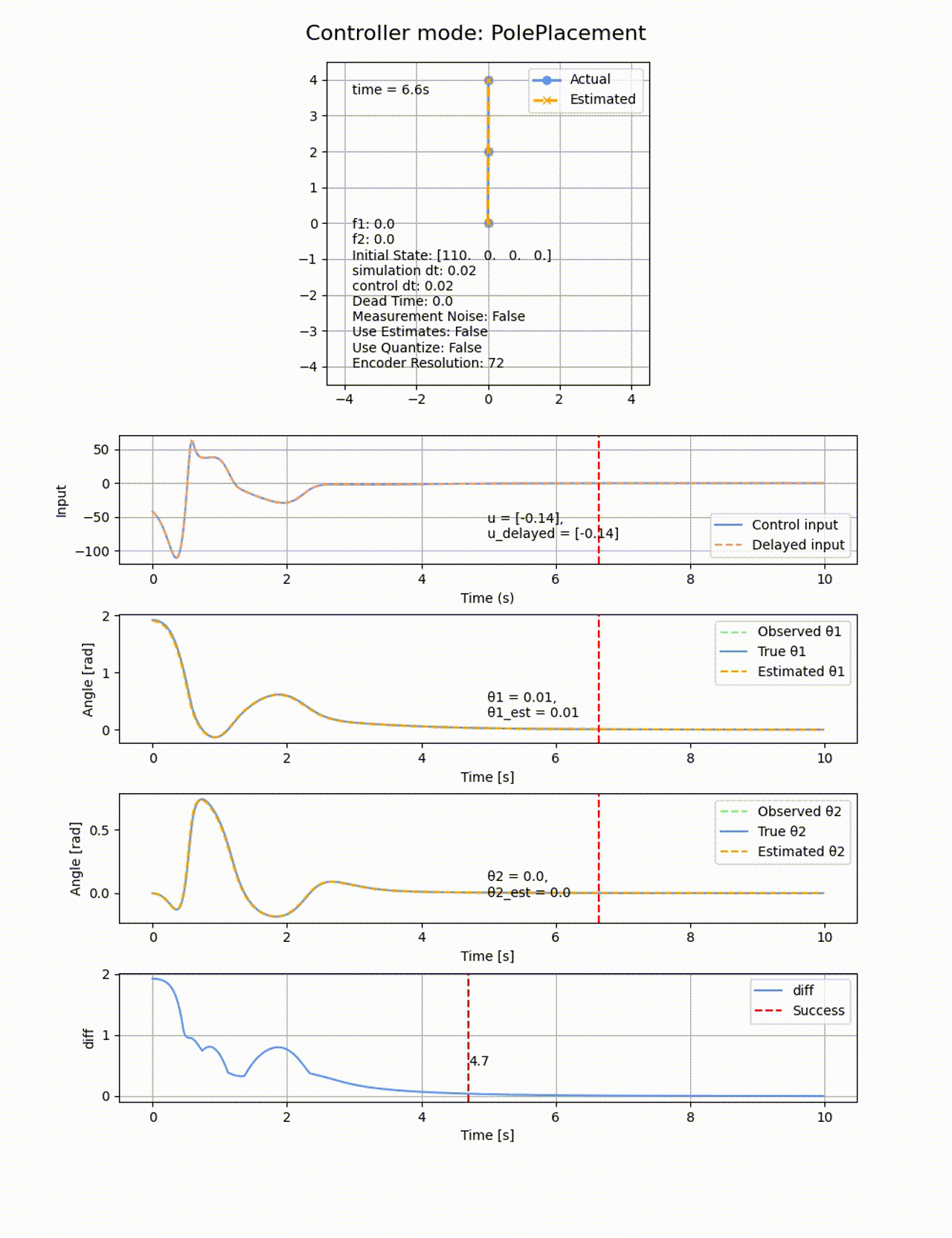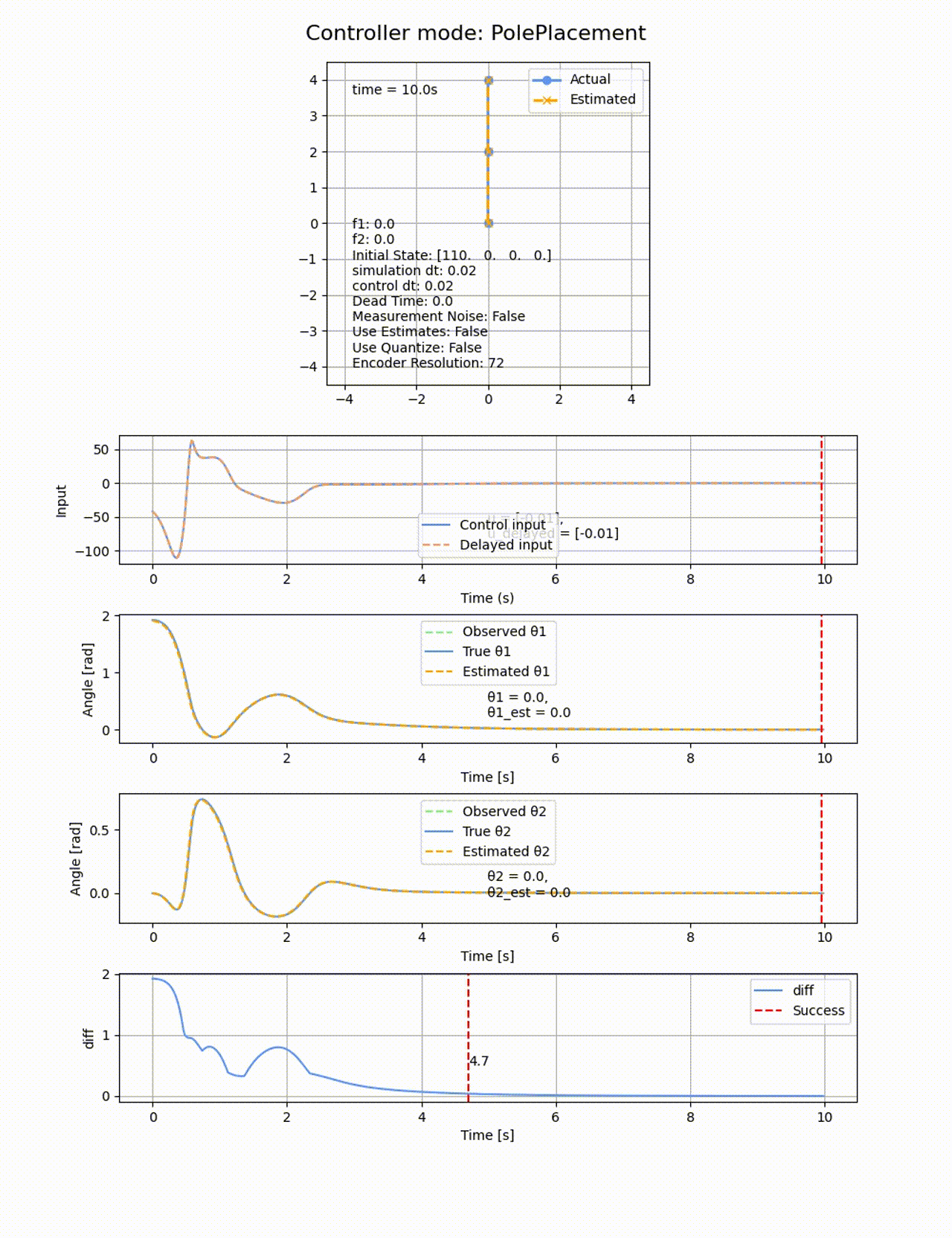
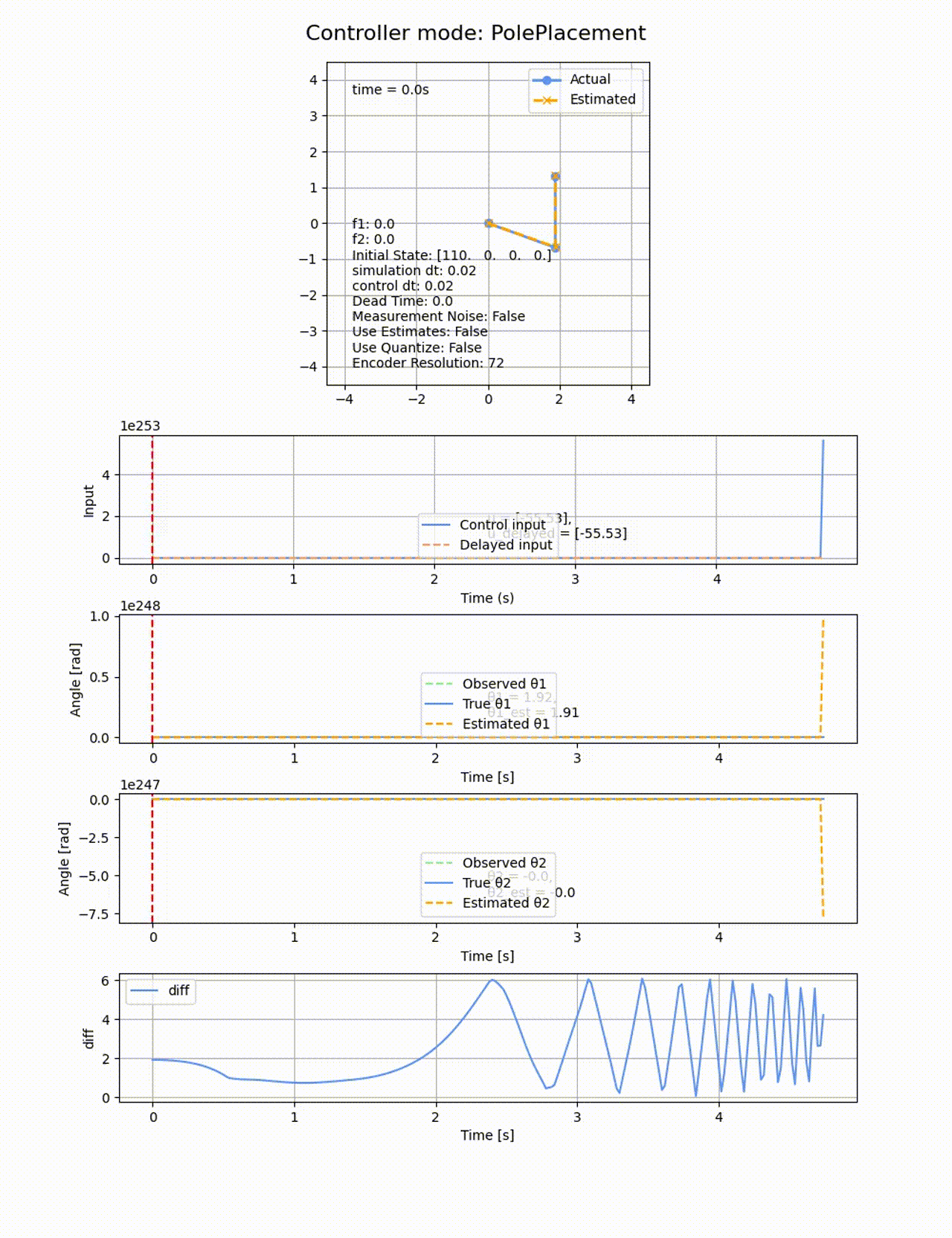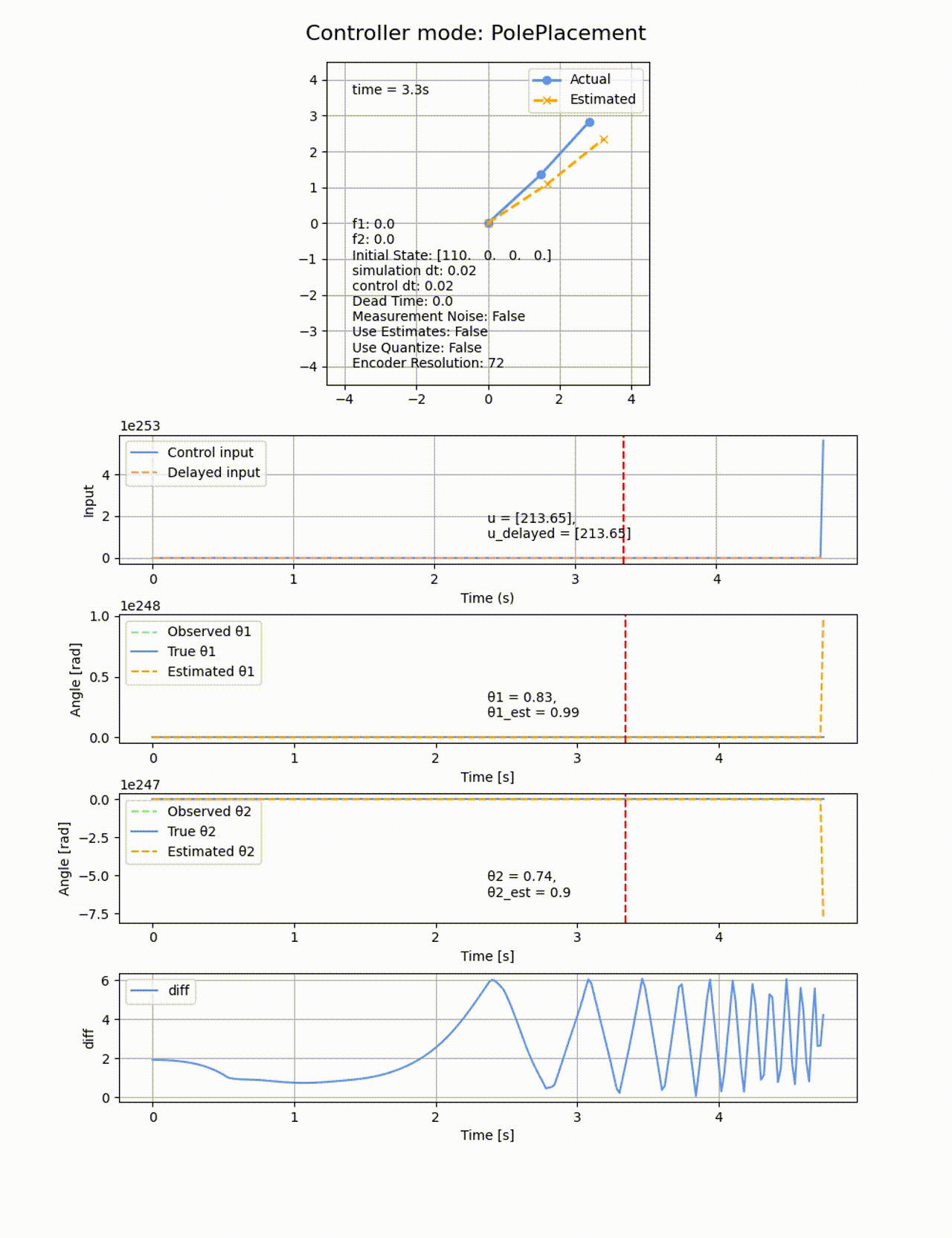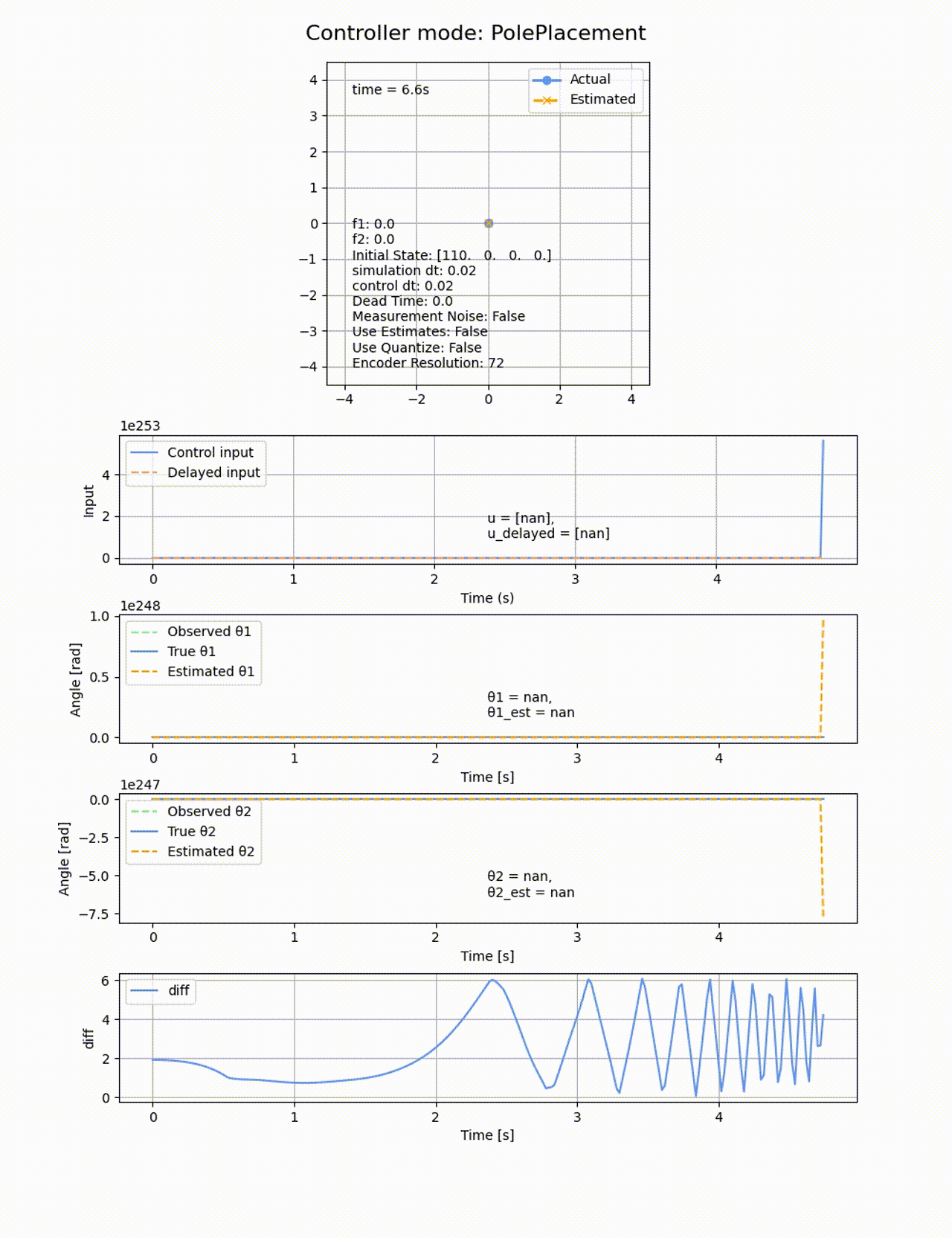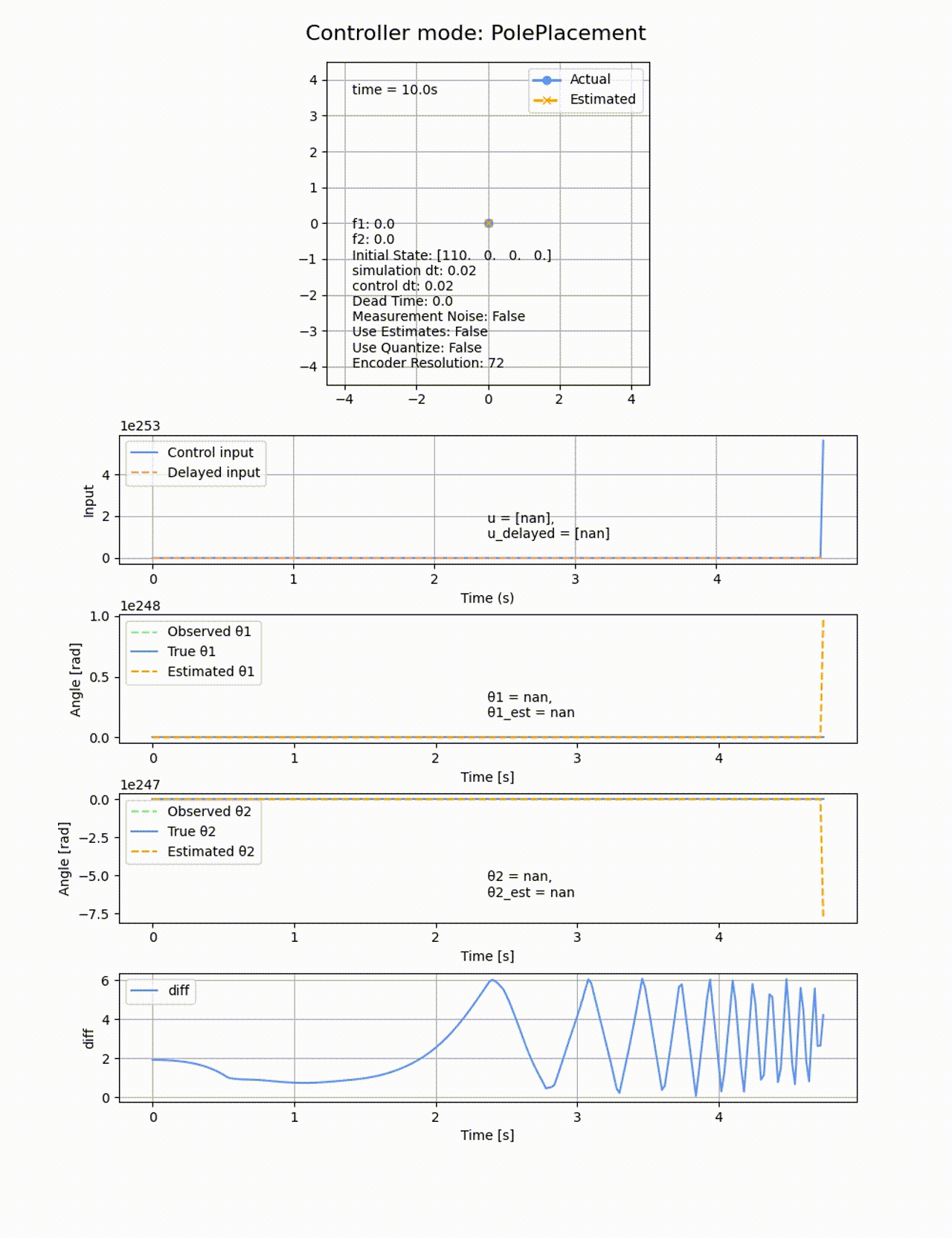
極の位置を変えると上手く制御できなくなります。例えば0.5倍して[-0.5, -1, -1.5, -2] にすると以下のようになります。2倍したときも同様に失敗します。
ROAを以下の通りで、大きめな角度からも成功します。連続的な範囲で成功するのでなくて、

LQR
LQR(Linear Quadratic Regulator)制御は、制御システムの設計方法の一つで、特に線形システムの最適制御に用いられます。この制御手法は、システムの状態を調整して、ある目的関数を最小化するように動作させることを目的としています。
LQRに関する解説は以下の記事も詳しいため参考にしてください。
LQR制御の基本的なアイデアは、システムの状態
ここで、
-
Q -
R
このコスト関数は、システムが目標状態に近づくため、すなわち状態偏差と制御入力を最小化するように設計されています。
LQR制御では、最適な制御入力
ここで、
LQRは線形システムに最適化されており、非線形システムに対してはそのまま適用することができません。そこで、先ほどの0度付近で線形化した状態空間モデルを使ってLQR制御を適用します。リカッチ方程式の解法はいくつかのライブラリでも関数が提供されており、例えばscipyではsolve_continuous_are(A, B, Q, R)とするだけで解けます。
import numpy as np
import control
from controller.base import Controller
from scipy.linalg import solve_continuous_are
from numpy.linalg import inv
class LQRController(Controller):
def __init__(self, A, B, Q, R, dt):
super().__init__(dt)
self.K = self._calculate_lqr_gain(A, B, Q, R)
def _calculate_lqr_gain(self, A, B, Q, R):
X = solve_continuous_are(A, B, Q, R)
K = inv(R) @ B.T @ X
return K
def control(self, state, desired_state, t):
if (
self.last_update_time is None
or np.round(t - self.last_update_time, 2) >= self.dt
):
self.last_update_time = t
self.u = -self.K @ (state - desired_state)
return self.u
初期値
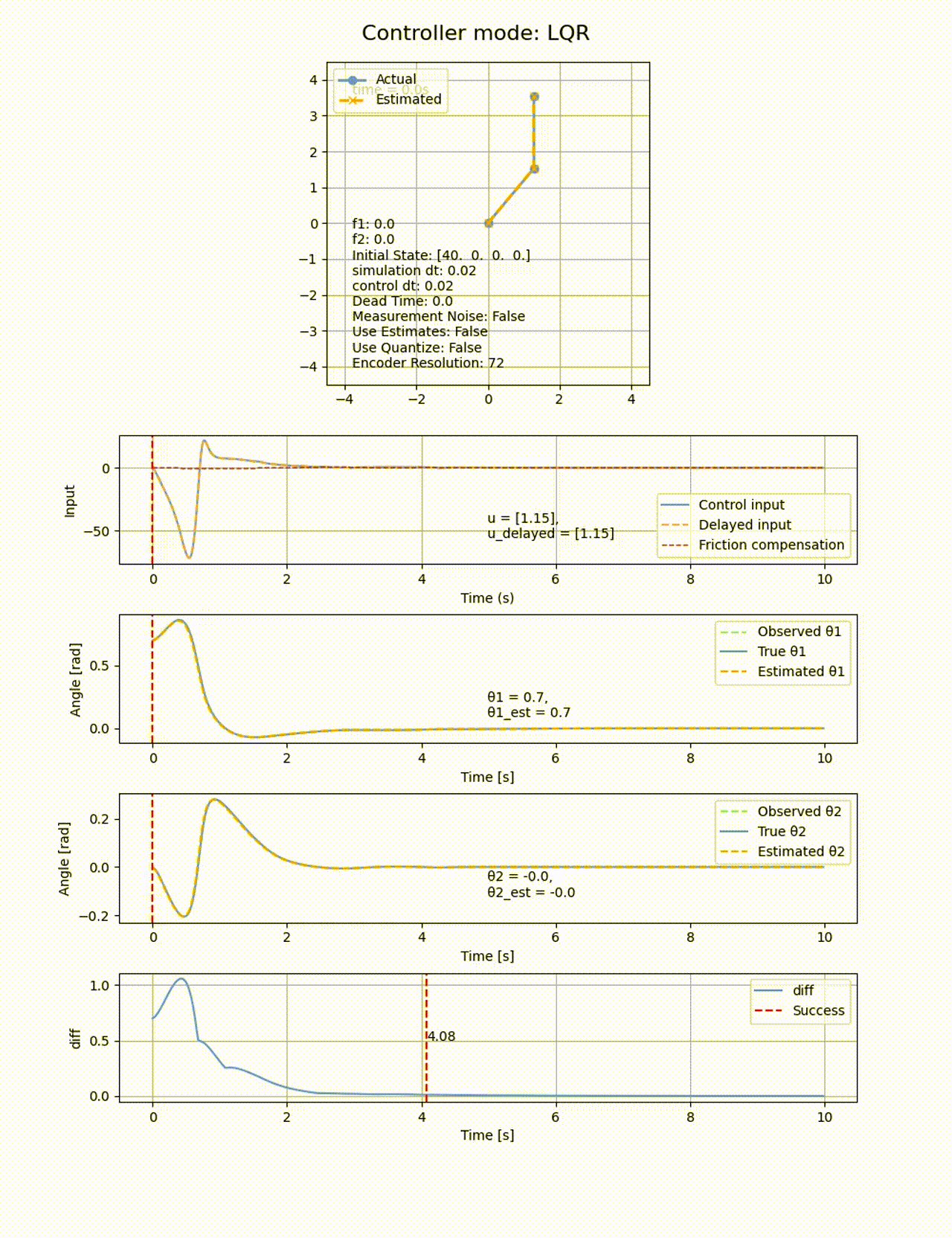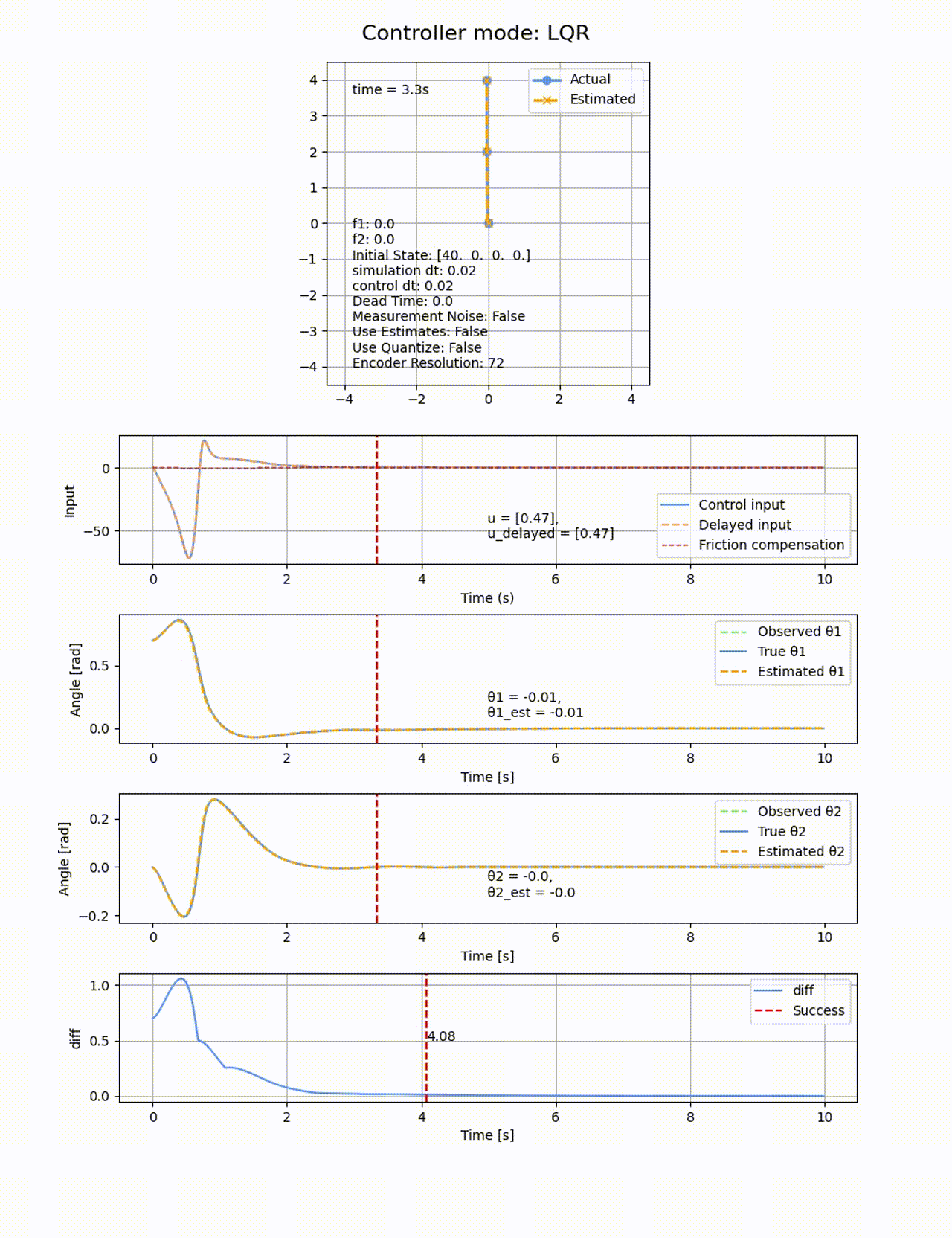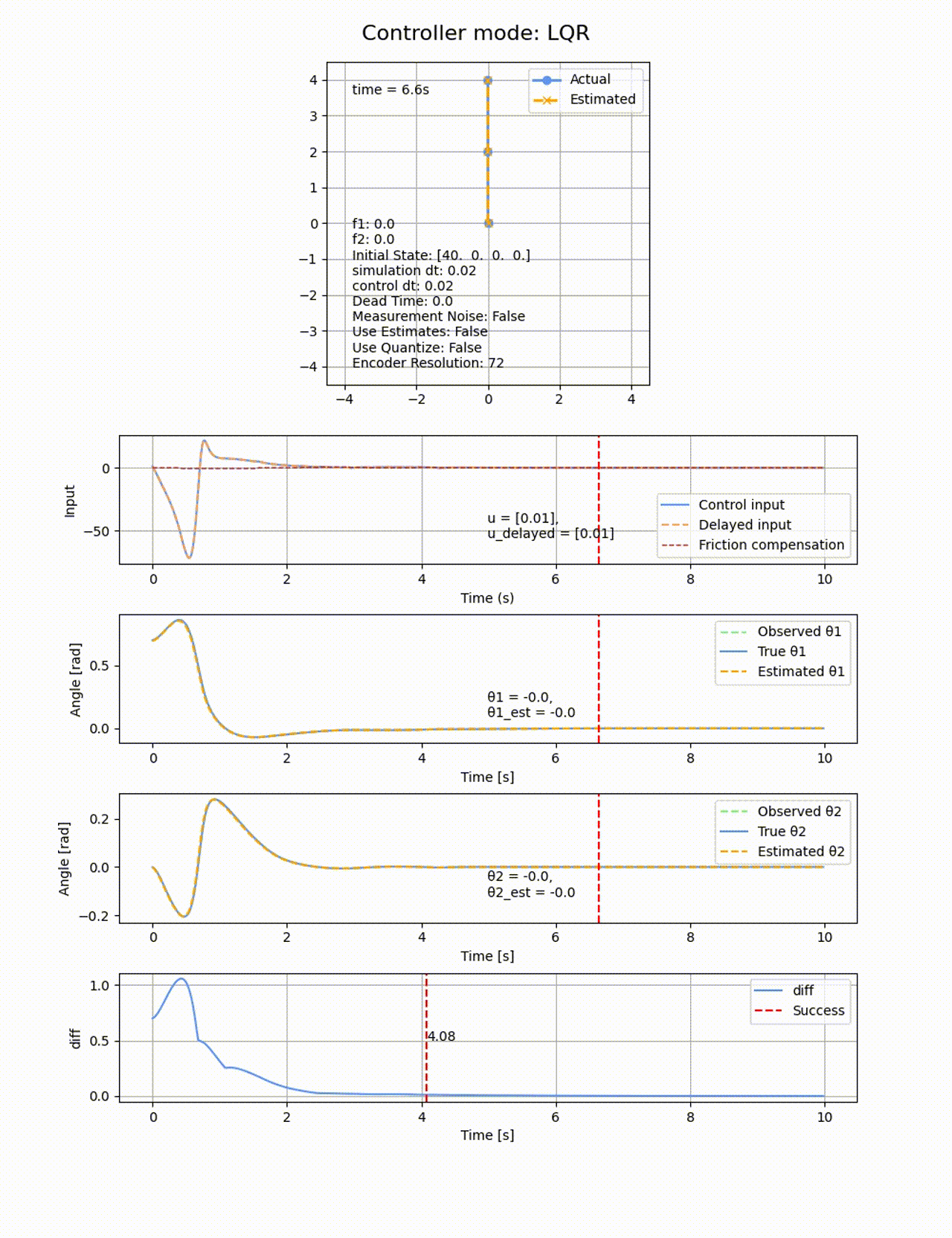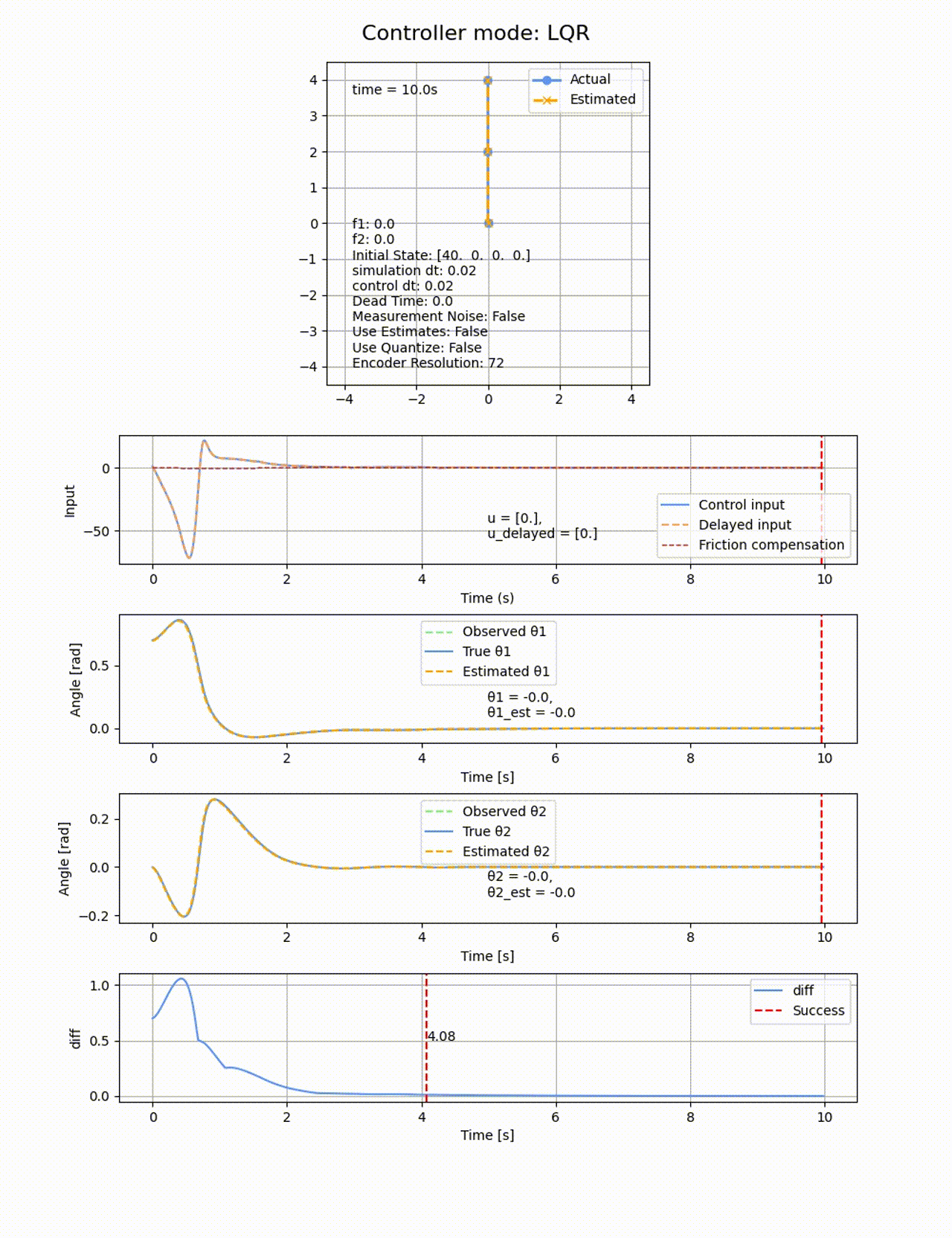
ROAは極配置に比べると小さくなりました。

iLQR
iLQR(Iterative Linear Quadratic Regulator)制御は、非線形システムの最適制御を行うための手法です。線形システムに適用されるLQRを非線形システムにも適用できるように拡張したものです。反復的に線形近似を行うことで、非線形システムの最適制御入力を求めます。
iLQRに関する詳細な解説は以下の記事が参考になりました。
iLQR制御の基本的なアイデアは、非線形システムの状態
ここで、
-
Q -
R -
Q_f
このコスト関数は、システムが目標状態に近づくため、状態偏差と制御入力を最小化するように設計されています。
iLQRは以下のステップで進行します。
-
初期軌道と入力の設定:
- 初期状態
x_0 \{u_0, u_1, ..., u_{N-1}\}
- 初期状態
-
フォワードパス(初期軌道):
- 現在の入力シーケンスを使ってシステムの状態軌道
\{x_0, x_1, ..., x_N\}
- 現在の入力シーケンスを使ってシステムの状態軌道
-
バックワードパス:
- 状態と入力に関するコスト関数を二次近似し、微分動的計画法(DDP)を用いて逆向きに最適化します。この過程で、ベルマン方程式に基づく最適性条件を用いて、フィードバックゲインとフィードフォワード補正項を計算します。
-
フォワードパス(軌道更新):
- バックワードパスで得られたフィードバックゲインとフィードフォワード補正項を使い、新しい入力シーケンスを生成し、状態軌道を更新します。
-
収束判定:
- コスト関数の変化量が十分に小さければ終了し、そうでなければステップ3に戻ります。
2の初期状態軌道を求める際には、2周期目以降であれば前回結果を使うことが多いですが、1周期目に初期値0とすると実際の解との差分が大きくなり、解が求まらないことがありました。その場合は、状態軌道付近で線形化を行いながら予測ホライゾンに渡ってLQRを逐次的に解いて状態軌道と入力軌道を求めて、iLQRの初期値として使うことも有効でした。
大きめなライブラリにはiLQRが実装されているものが見つからず、今回は
を使用しました。Numbaによる高速化も行われています。forkしてpip install出来るようにしたものが以下になります。
numpy.arrayの状態と入力を渡すだけなので、とても使いやすいインターフェイスです。
xs, us, cost_trace = controller.fit(x0, us_init)
制御側にもフォワードパスで状態軌道を計算するために、モデルを渡す必要があります。ここではシミュレーター側が持つと同じものをiLQR内部にも定義します。ただし、iLQRは最適化に微分を用いるため、非連続な動摩擦部分の項は削除しています。また、本来であればモデルは未知であるため、システム同定等を行って求める必要があります。
実装したコードは以下の通りです。
from ilqr import iLQR
from ilqr.containers import Dynamics, Cost
import numpy as np
class ILQRControllerNumba(Controller):
def __init__(
self,
dynamics,
desired_state,
Q,
R,
QT,
N,
dt,
horizon_dt,
maxiters=50,
early_stop=True,
):
super().__init__(dt)
self.maxiters = maxiters
self.early_stop = early_stop
c1 = dynamics.c1
c2 = dynamics.c2
alpha1 = dynamics.alpha1
alpha2 = dynamics.alpha2
alpha3 = dynamics.alpha3
alpha4 = dynamics.alpha4
alpha5 = dynamics.alpha5
def f(x, u):
theta1, theta1_dot, theta2, theta2_dot = x
theta12 = theta1 - theta2
cos_theta12 = np.cos(theta12)
sin_theta12 = np.sin(theta12)
denominator = alpha1 * alpha2 - alpha3**2 * cos_theta12**2
if denominator == 0:
raise ValueError("Denominator is zero, causing division by zero")
theta1_ddot = (
-alpha2 * alpha3 * sin_theta12 * theta2_dot**2
+ alpha2 * alpha4 * np.sin(theta1)
- alpha2 * c1 * theta1_dot
- alpha2 * c2 * theta1_dot
+ alpha2 * c2 * theta2_dot
+ alpha2 * u[0]
- alpha3**2 * sin_theta12 * cos_theta12 * theta1_dot**2
- alpha3 * alpha5 * np.sin(theta2) * cos_theta12
- alpha3 * c2 * cos_theta12 * theta1_dot
+ alpha3 * c2 * cos_theta12 * theta2_dot
) / denominator
theta2_ddot = (
alpha1 * alpha3 * sin_theta12 * theta1_dot**2
+ alpha1 * alpha5 * np.sin(theta2)
+ alpha1 * c2 * theta1_dot
- alpha1 * c2 * theta2_dot
+ alpha3**2 * sin_theta12 * cos_theta12 * theta2_dot**2
- alpha3 * alpha4 * np.sin(theta1) * cos_theta12
+ alpha3 * c1 * cos_theta12 * theta1_dot
+ alpha3 * c2 * cos_theta12 * theta1_dot
- alpha3 * c2 * cos_theta12 * theta2_dot
- alpha3 * u[0] * cos_theta12
) / denominator
dxdt = np.array(
[theta1_dot, theta1_ddot, theta2_dot, theta2_ddot], dtype=np.float64
)
return x + dxdt * horizon_dt
cost = Cost.QR(Q, R, QT, desired_state)
discrete_dynamics = Dynamics.Discrete(f)
self.iLQR = iLQR(discrete_dynamics, cost)
self.u = np.zeros((N, 1))
def control(self, state, desired_state, t):
if (
self.last_update_time is None
or jnp.round(t - self.last_update_time, 2) >= self.dt
):
self.last_update_time = t
xs, us, cost_trace = self.iLQR.fit(state, self.u, maxiters=self.maxiters, early_stop=self.early_stop)
self.u = us
return self.u[0]
Q=diag([100, 1, 100, 1]), R=diag([0.1]) として、ホライゾンは2秒間(N=20, horizon_dt=0.1)として、初期値
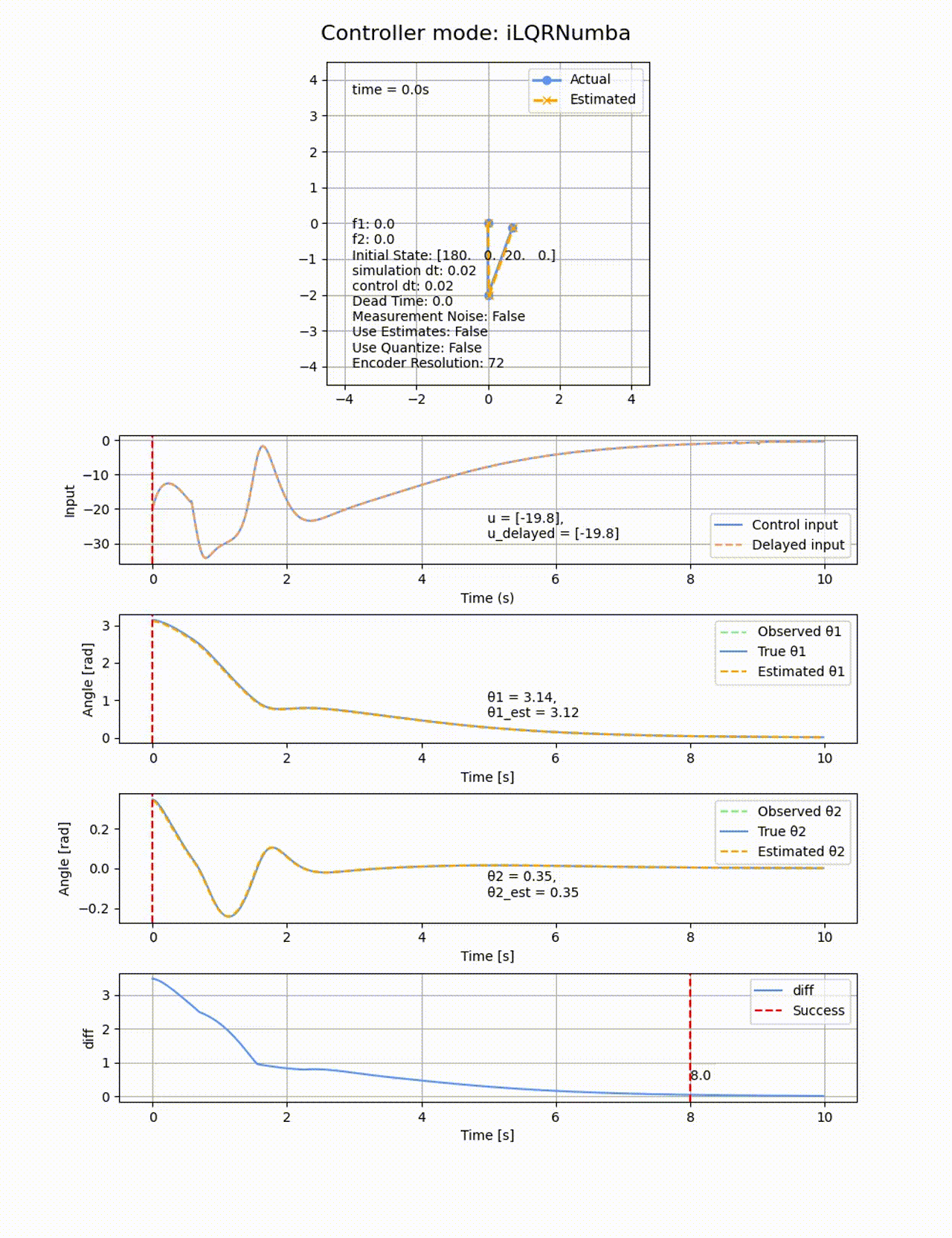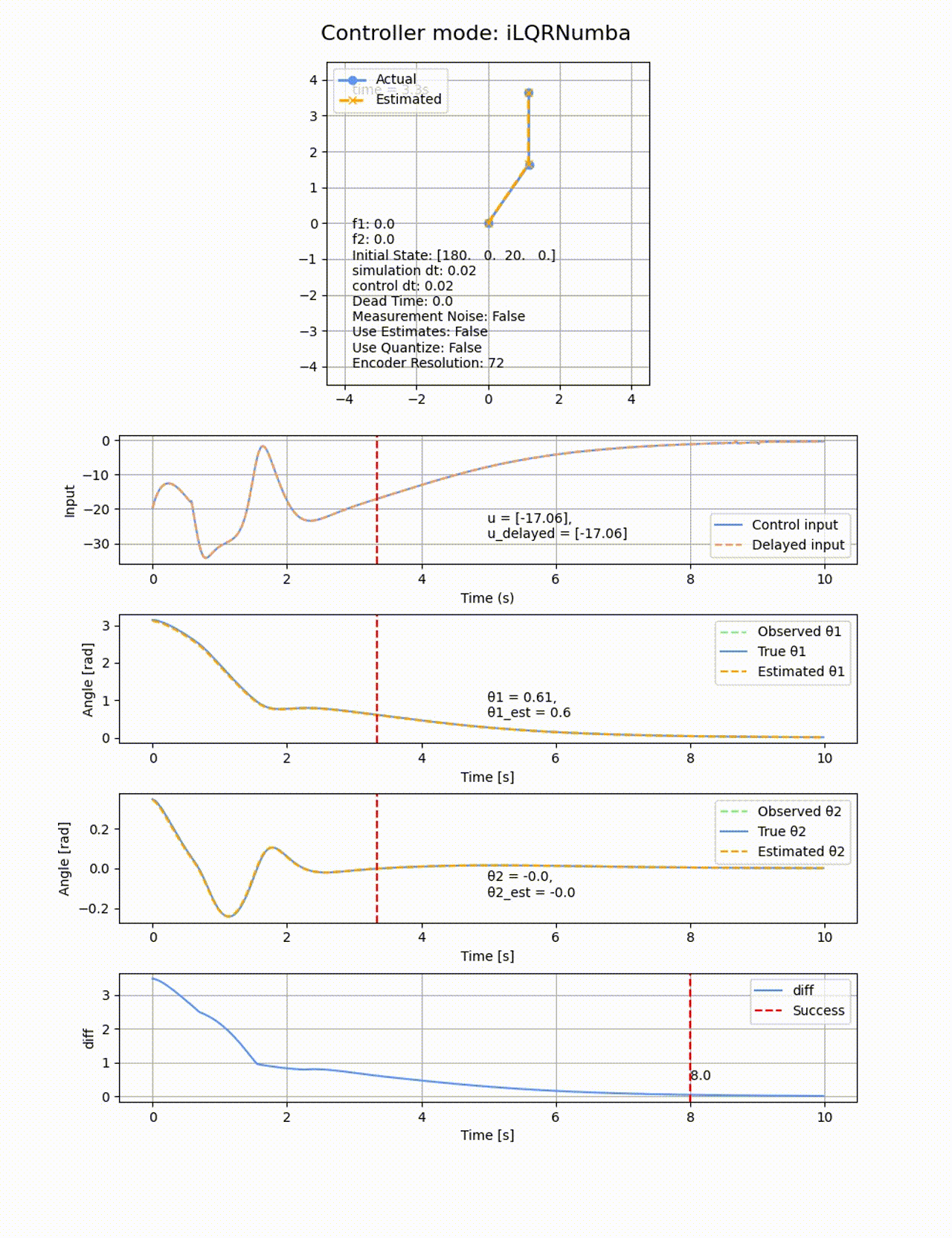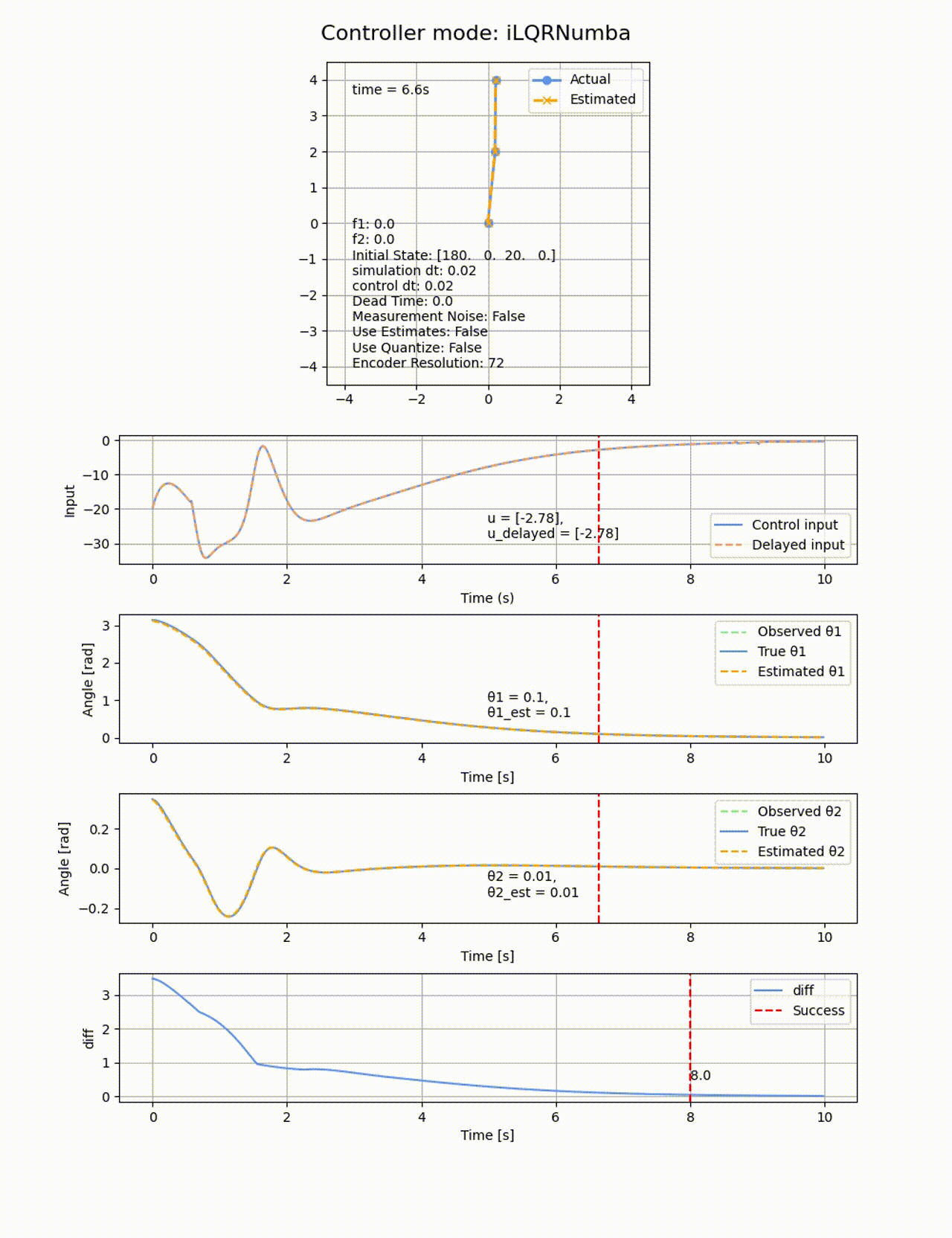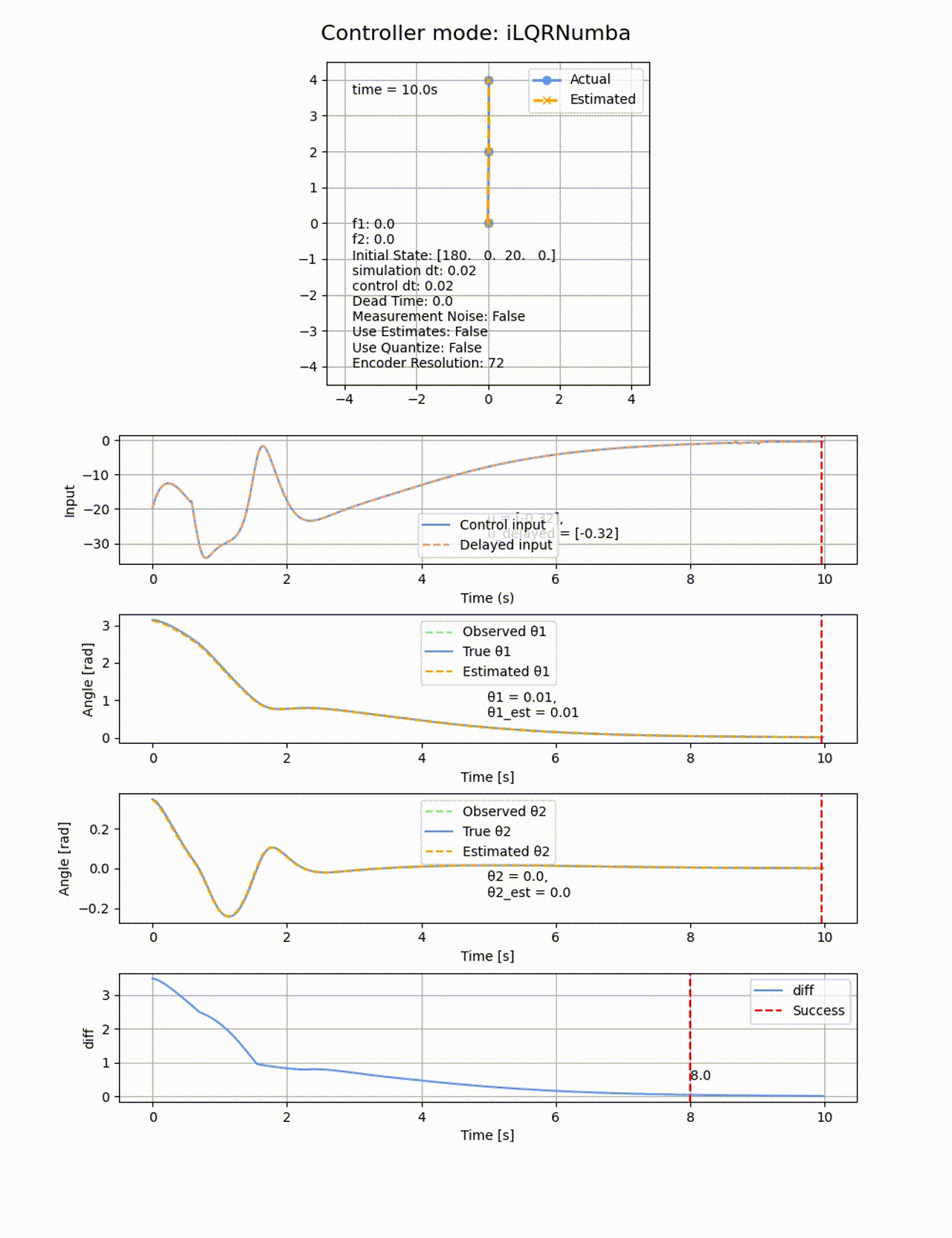
ROAは以下の通りです。LQRでは0度付近でモデルを線形化していたため、この付近から離れた角度では上手く制御が出来ませんでしたが、iLQRは非線形モデルを使っているため、より広い範囲で成功しています。最後の制御がゆっくりなので、10sの時間以内に収束判定されていない可能性があります。重みの調整や制御時間伸ばせばさらに広いROAの結果が得られたかもしれません。トータルの計算時間はLQRが0.3s程度であるのに対して、iLQRは22.97sと大幅に増加しています。ただし高速化の余地は大いに残っています。

線形MPC
Model Predictive Control(MPC)は、動的システムの制御において使用される制御手法です。MPCは、将来の時間ステップにおけるシステムの動作を予測し、予測された挙動に基づいて最適な制御入力を決定するという特徴を持っています。また制約条件を直接扱うことが出来ます。
MPCに関する解説は以下の記事も詳しいため参考にしてください
MPCの基本的なアイデアは以下の通りです。
-
モデルベースの予測:
- システムの動的モデルを用いて、未来の複数の時間ステップにわたるシステムの挙動を予測します。
-
最適化問題を解く:
- 予測された未来のシステム状態と制御入力のシーケンスに対して、与えられたコスト関数を最小化する制御入力を計算します。コスト関数は、通常、状態の偏差と制御入力の大きさを反映します。
-
制御入力の適用:
- 計算された最適な制御入力の中から、最初の入力のみを実際のシステムに適用します。
-
再予測とフィードバック:
- 次の時間ステップで再度システムの状態を観測し、新たな最適化問題を解きます。このプロセスを繰り返すことで、常に最新の情報に基づいた制御を実現します。
MPCでは、以下のような一般的な二次形式のコスト関数
ここで、
-
x(t) t -
u(t) t -
Q -
R -
Q_f
線形MPCとは、「1.モデルベースの予測」において、線形化されたモデルを使って予測軌道も計算する手法になります。
例えば、自動運転OSSのAutowareでは経路追従のためのステア制御に線形MPCが使われています。経路追従問題においては、軌道近傍のダイナミクスに変換し、そこで追従誤差が微小という仮定を用いて、線形化を行っています。
線形MPCでの最適化問題は、線形制約付きの二次計画問題(Quadratic Programming, QP)として定式化され、非線形最適化 (Nonlinear Programming, NLP) に比べて高速に安定して解くことが出来ます。
最適化問題の範囲の関係は以下になります。
非線形計画法(NLP) ⊃ 凸最適化 ⊃ 錐計画法(CP) ⊃ 二次計画法(QP) ⊃ 線形計画法(LP)
- 非線形計画法(NLP)
- 少なくとも一つの非線形制約または非線形目的関数を持つ最適化問題を扱います。
- 凸最適化 (Convex Optimization)
- 非線形計画法のサブセットで、目的関数と制約が凸関数である最適化問題を扱います。局所最適解が大域最適解となる特性があります。
- 錐計画法(CP)
- 凸最適化のサブセットで、目的関数と制約が錐の形状をしている最適化問題を扱います。
- 二次計画法(QP)
- 錐計画法のサブセットで、目的関数が二次関数(通常は凸二次関数)、制約が線形である最適化問題を扱います。
- 線形計画法(LP)
- 錐計画法のサブセットで、目的関数と制約が線形である最適化問題を扱います。
より狭い問題に落とし込み、それ専用のソルバーを使うことで、高速に解くことができます。
二次計画問題のソルバーとしては、OSQPやqpOASESなどが有名です。OSQPはオープンソースのQPソルバーで、特に大規模で疎な問題に適しています。qpOASESは商用ライセンスのソルバーで、小規模な問題に対して高速な処理が可能です。
Pythonの凸最適化ライブラリとしてはCVXPYが有名です。このライブラリではOSQPの他に
- ECOS: 円錐計画法(LP、QP、SOCP)に適している。
- SCS: 大規模でスパースな錐計画法に適している。
のソルバーがあり、デフォルトではECOSになります。今回は二次計画問題ソルバーに特化したOSQPを使います。
import numpy as np
import cvxpy as cp
class MPCController(Controller):
def __init__(self, A, B, Q, R, N, dt, horizon_dt):
super().__init__(dt)
self.A = A
self.B = B
self.Q = Q
self.R = R
self.N = N # Prediction horizon
self.dt = dt # Control period
self.horizon_dt = horizon_dt # Horizon period
self.nx = A.shape[0]
self.nu = B.shape[1]
# Discretize system with horizon_dt for prediction
self.Ad = np.eye(A.shape[0]) + A * horizon_dt
self.Bd = B * horizon_dt
self.cp_U = cp.Variable((self.N, self.nu))
def predict_state(self, x, u):
return self.Ad @ x + self.Bd @ u
def control(self, state, desired_state, t):
if (
self.last_update_time is None
or np.round(t - self.last_update_time, 2) >= self.dt
):
self.last_update_time = t
x0 = state
ref = desired_state
cost = 0
constraints = []
x = x0
for i in range(self.N):
u = self.cp_U[i, :]
x = self.predict_state(x, u)
cost += cp.quad_form(x - ref, self.Q) + cp.quad_form(u, self.R)
constraints += [self.cp_U <= 100.0, self.cp_U >= -100.0]
problem = cp.Problem(cp.Minimize(cost), constraints)
problem.solve(solver=cp.OSQP)
self.u = self.cp_U.value[0, :]
return self.u
ここで予測時間間隔(horizon_dt)おきに離散時間での予測を行うため、離散時間システムとしてモデル化する必要があります。Ad, Bdはオイラー法によって離散化した際のシステム行列になります。
連続時間システムの状態方程式を次のように近似します。
したがって、離散時間システム行列
MPCのパラメタは、
Q_mpc = np.diag([10, 1, 10, 1])
R_mpc = np.diag([0.01])
N = 10
horizon_dt = 0.2
として、
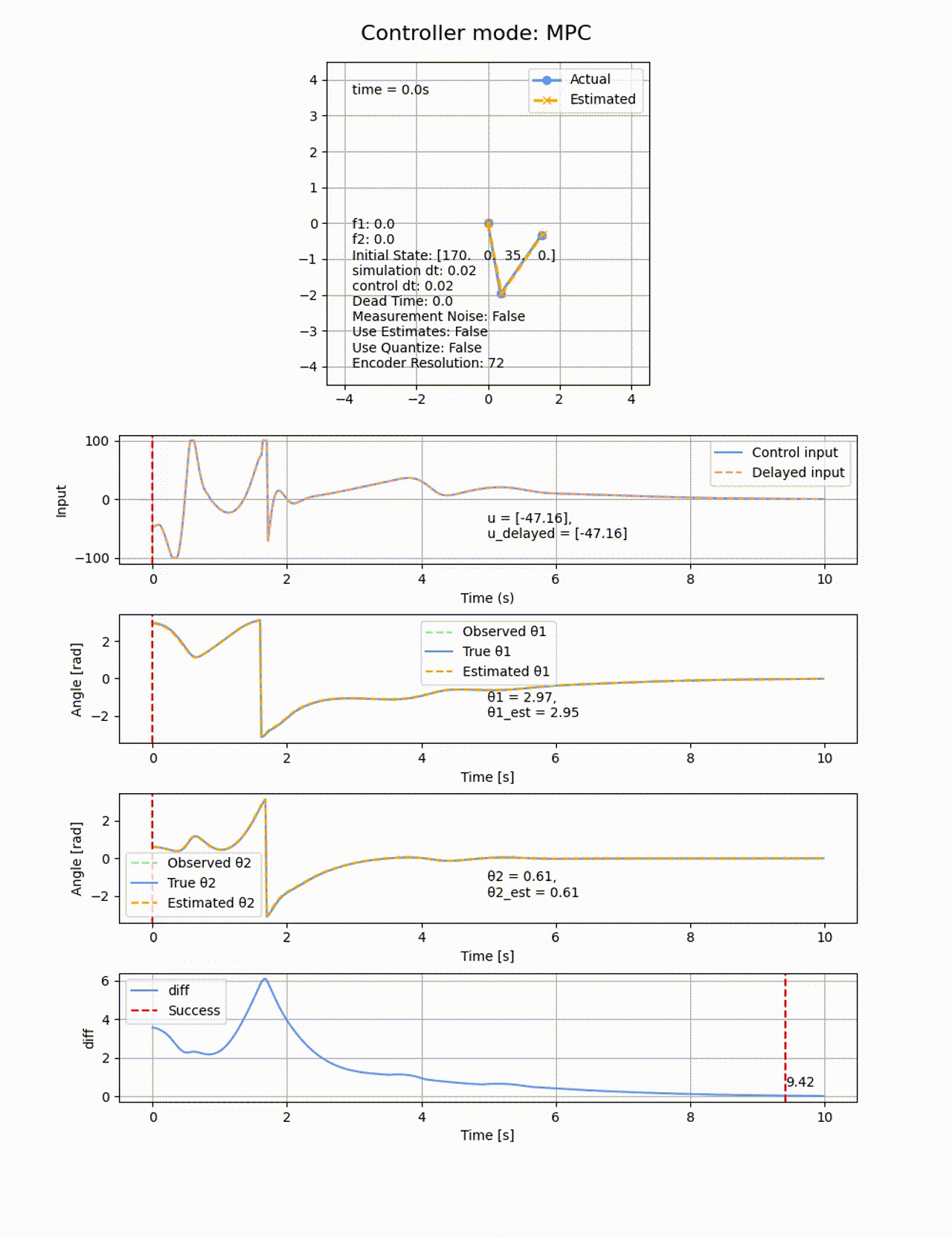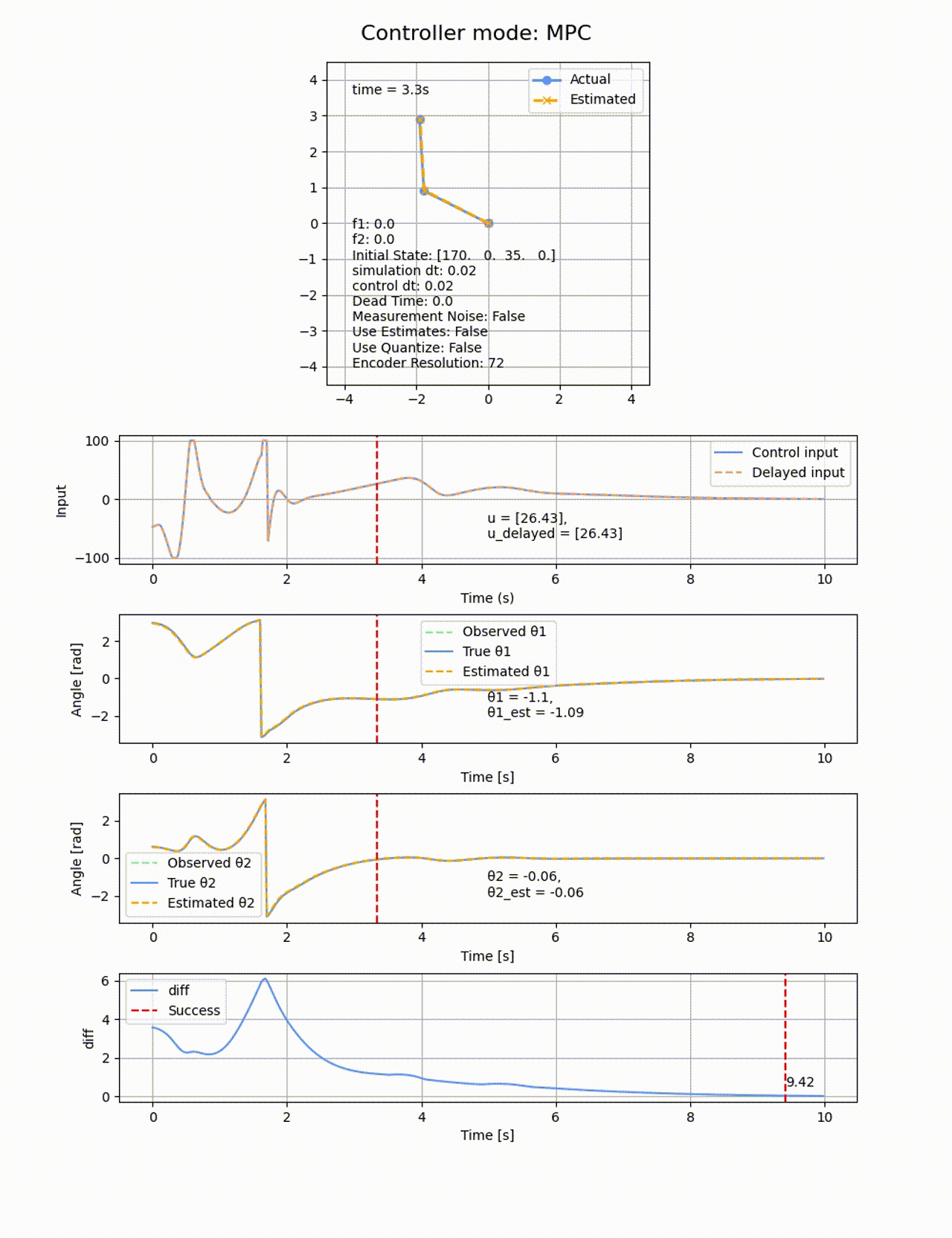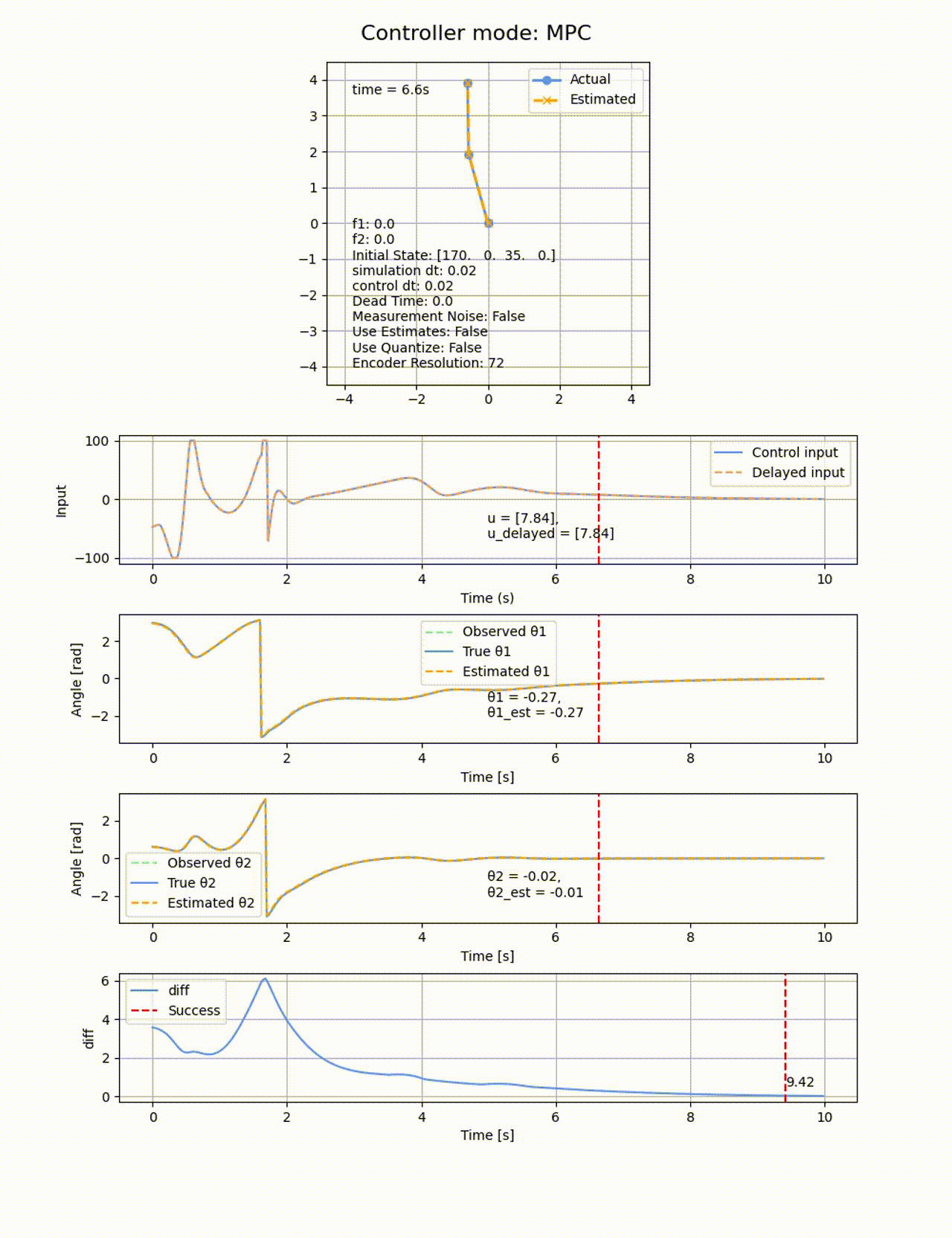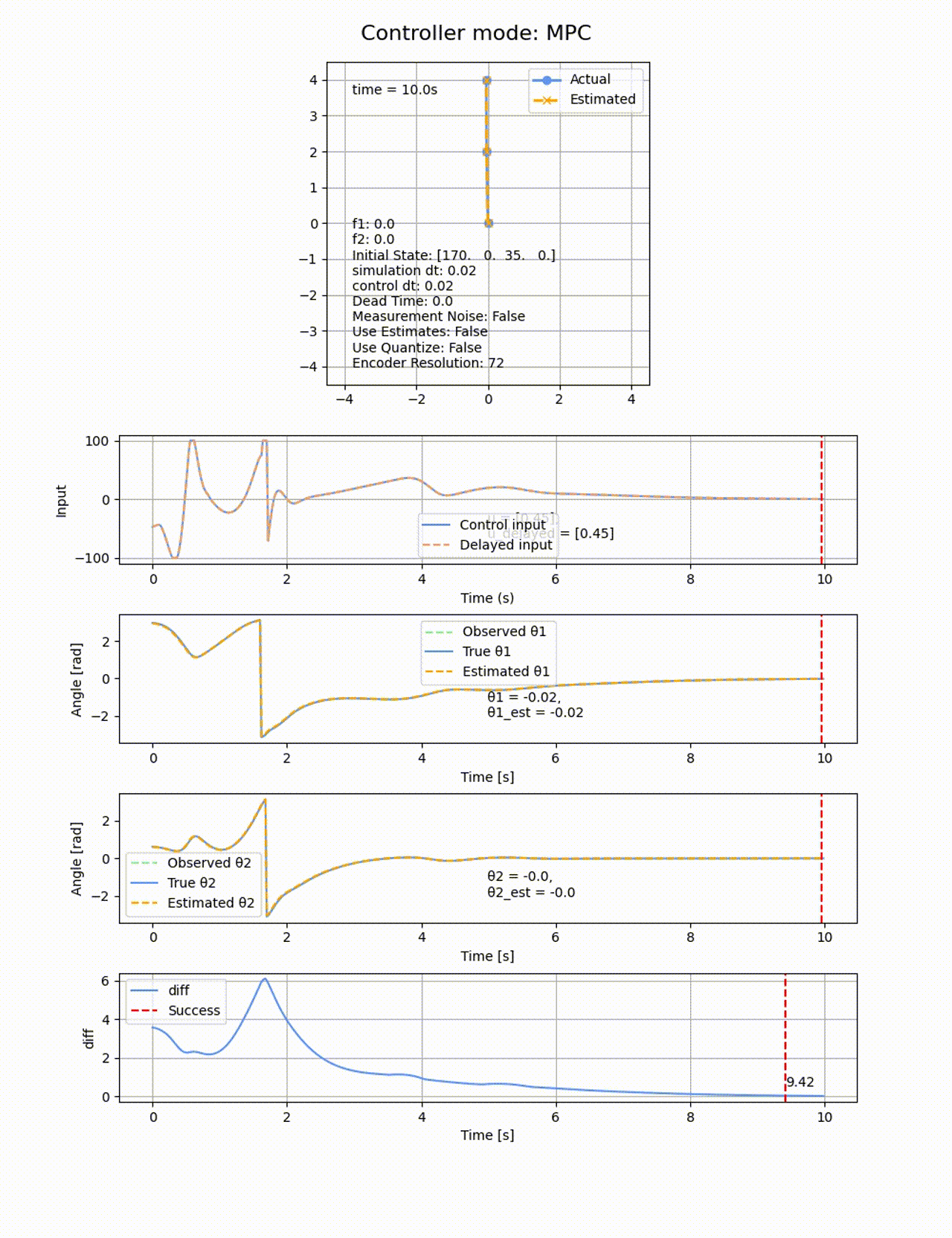
ROAを見てもその様子が分かります。自分で振り上げが出来ているのは、

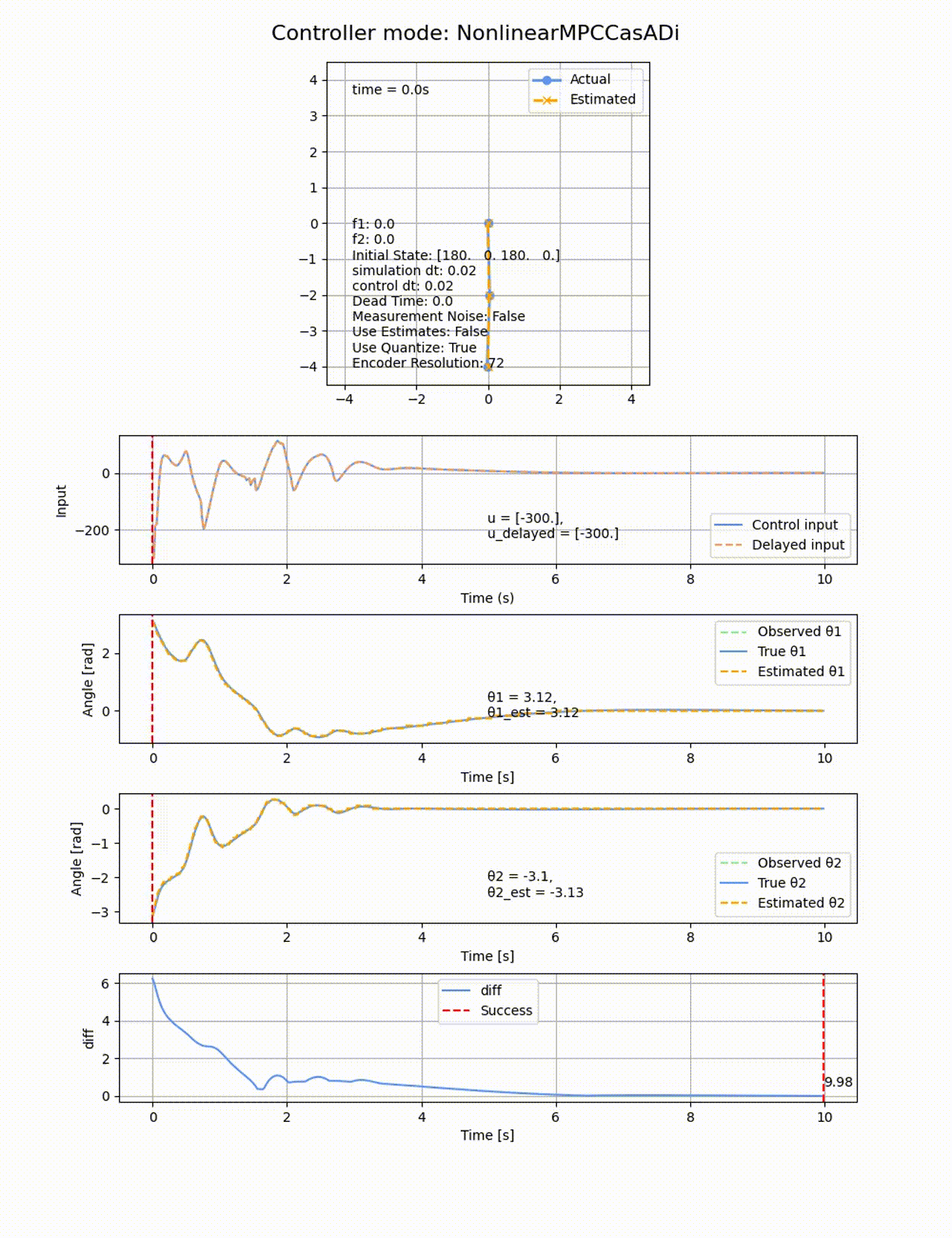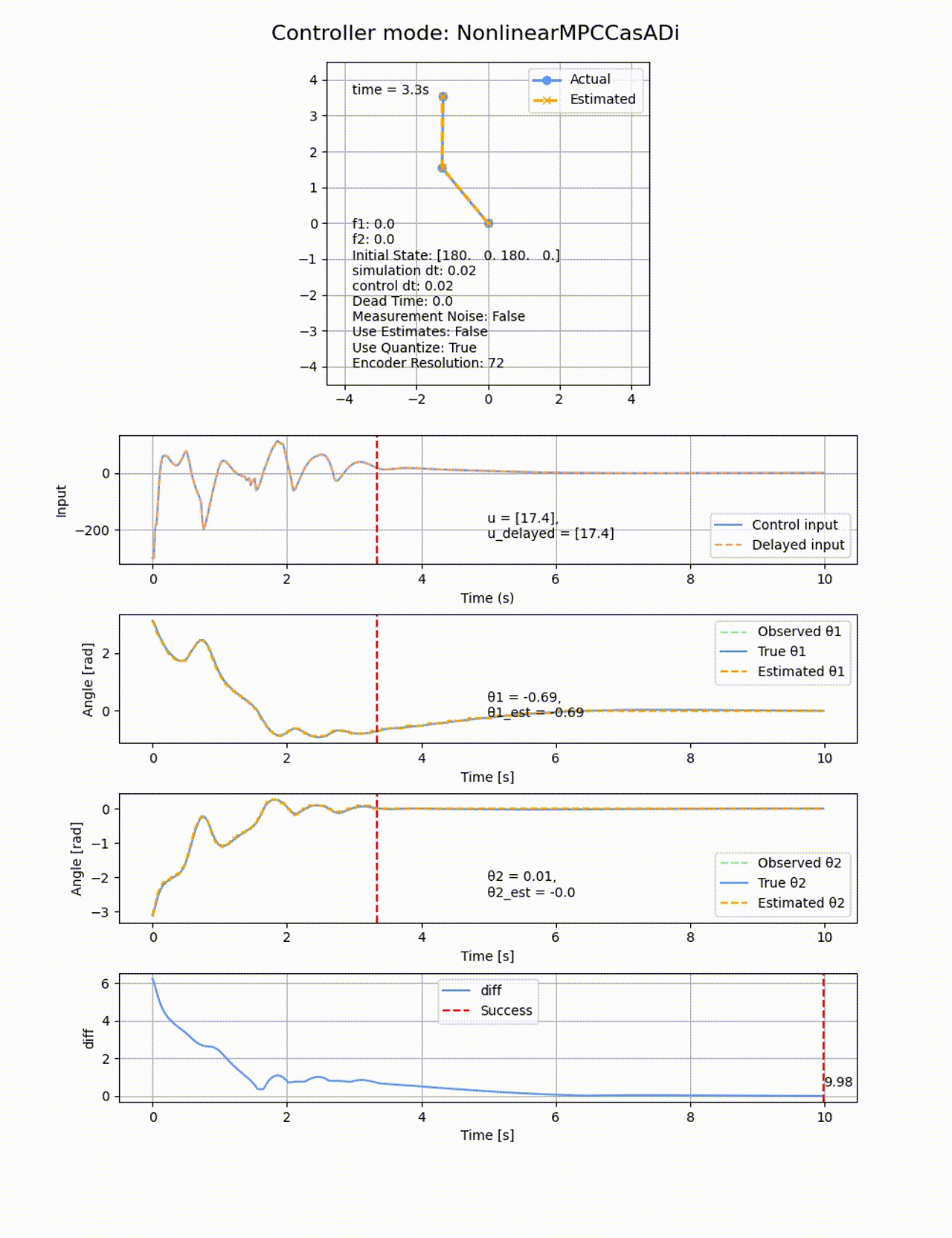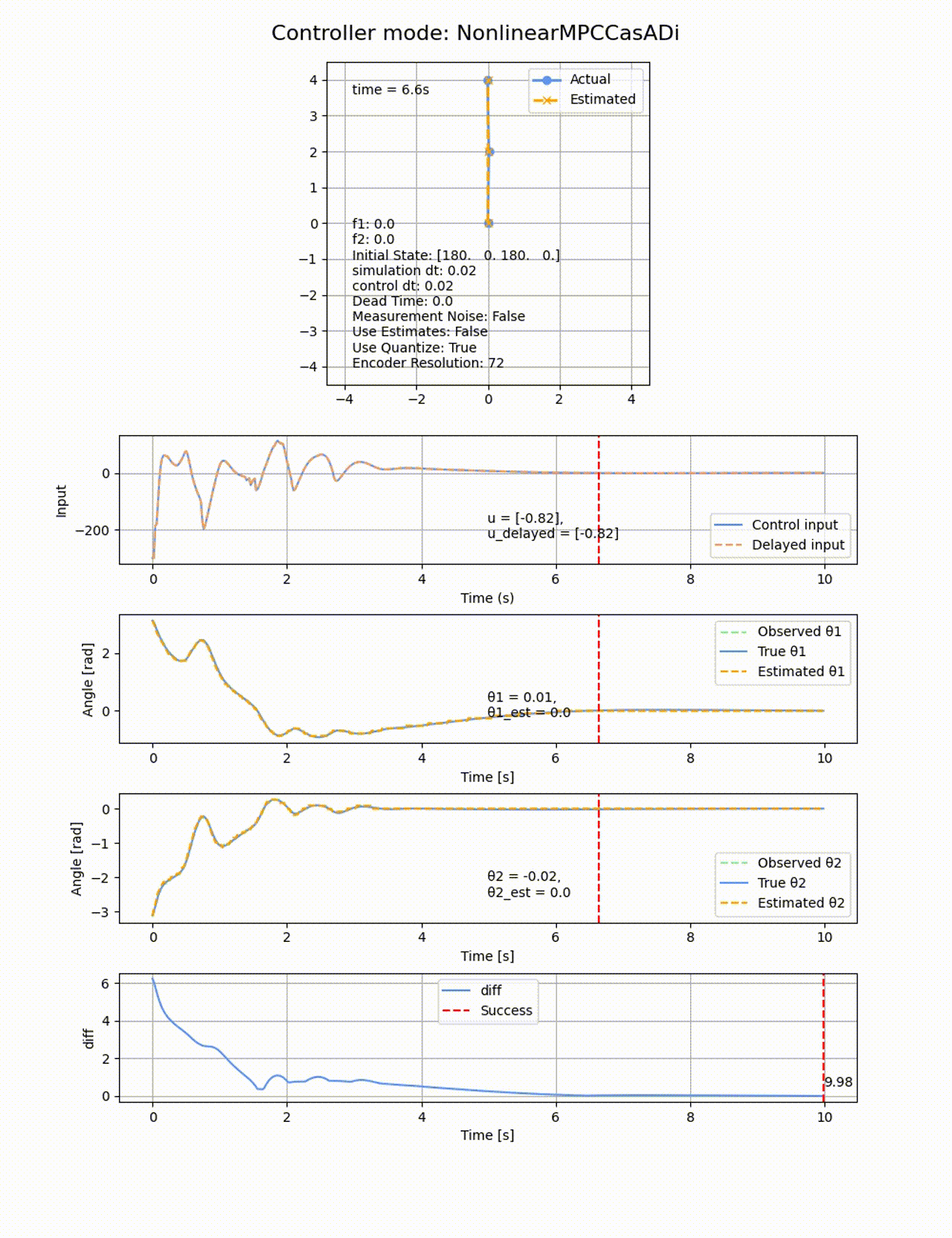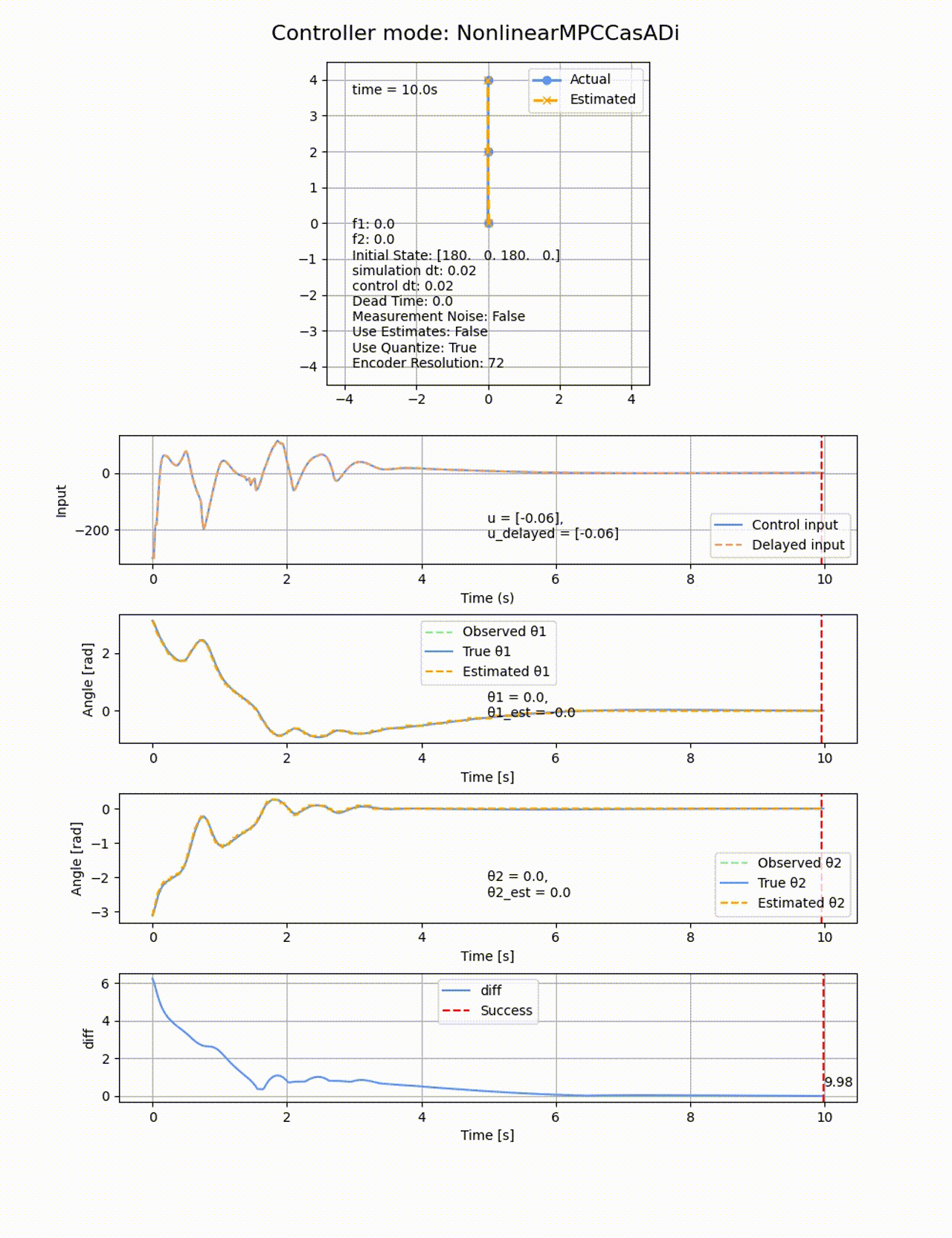
非線形MPC
非線形MPCは、非線形モデルを予測に用いて、コスト関数を非線形最適化で解く方法になります。線形MPCでは0度付近で線形化したモデルを使用したため、角度が大きくなった際に上手く制御が出来ない場合がありましたが、非線形性を直接扱うことでより広い範囲での制御ができます。ただし計算負荷が高かったり、数値解放の安定性や収束性が問題になることがあります。
実装にはCasADiを用います。CasAdiはsympyと同じようにシンボリックで数式を記述したり、微分計算を行ったり、最適化計算を行うことで出来るライブラリです。CasAdiを用いたMPCに関しては、PythonとCasADiで学ぶモデル予測制御が詳しいです。
非線形MPCにもiLQRの時と同様に、制御側に非線形モデルをそのまま与えてあげます。ここでCasAdiの変数として記述することで、最適化計算時に自動的に微分を計算してくれます。非線形最適化ソルバーにはIPOPTを使用します。IPOPTはオープンソースの非線形最適化ソルバーで、主双対内点法を用いて大規模な非線形最適化問題を解くことができます。主双対内点法 に関しては以下の記事が詳しいです。
import numpy as np
import casadi as ca
from controller.base import Controller
class NonlinearMPCControllerCasADi(Controller):
def __init__(
self, dynamics, A, B, Q, R, N, dt, horizon_dt, integration_method="rk4"
):
self.dynamics = dynamics
self.Q = Q
self.R = R
self.N = N # Prediction horizon
self.nx = A.shape[0]
self.nu = B.shape[1]
self.integration_method = integration_method
self.prev_u = np.zeros(self.nu)
self.horizon_dt = horizon_dt
self.dt = dt
self.last_update_time = None
self.u = np.zeros(self.nu)
self.alpha1 = dynamics.alpha1
self.alpha2 = dynamics.alpha2
self.alpha3 = dynamics.alpha3
self.alpha4 = dynamics.alpha4
self.alpha5 = dynamics.alpha5
self.f1 = dynamics.f1
self.f2 = dynamics.f2
self.c1 = dynamics.c1
self.c2 = dynamics.c2
# CasADi symbolic variables
self.state_sym = ca.MX.sym("state", self.nx)
self.u_sym = ca.MX.sym("u", self.nu)
self.dxdt_sym = self.f(self.state_sym, 0, self.u_sym)
self.f_func = ca.Function(
"f_func", [self.state_sym, self.u_sym], [self.dxdt_sym]
)
def predict_state(self, x, u, dt):
if self.integration_method == "euler":
return self.euler_step(self.f_func, x, dt, u)
elif self.integration_method == "rk4":
return self.runge_kutta_step(self.f_func, x, dt, u)
else:
raise ValueError("Invalid integration method. Choose 'euler' or 'rk4'.")
def euler_step(self, func, x, dt, u):
return x + dt * func(x, u)
def runge_kutta_step(self, func, x, dt, u):
k1 = func(x, u)
k2 = func(x + 0.5 * dt * k1, u)
k3 = func(x + 0.5 * dt * k2, u)
k4 = func(x + dt * k3, u)
y = x + (dt / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
return y
def cost_function(self, U, x0, ref):
x = x0
cost = 0
for i in range(self.N):
u = U[i * self.nu : (i + 1) * self.nu]
x = self.predict_state(x, u, self.horizon_dt)
cost += ca.mtimes([(x - ref).T, self.Q, (x - ref)]) + ca.mtimes(
[u.T, self.R, u]
)
return cost
def f(self, state, t, u):
theta1 = state[0]
theta1_dot = state[1]
theta2 = state[2]
theta2_dot = state[3]
theta12 = theta1 - theta2
cos_theta12 = ca.cos(theta12)
sin_theta12 = ca.sin(theta12)
denominator = self.alpha1 * self.alpha2 - self.alpha3**2 * cos_theta12**2
theta1_ddot = (
-self.alpha2 * self.alpha3 * sin_theta12 * theta2_dot**2
+ self.alpha2 * self.alpha4 * ca.sin(theta1)
- self.alpha2 * self.c1 * theta1_dot
- self.alpha2 * self.c2 * theta1_dot
+ self.alpha2 * self.c2 * theta2_dot
+ self.alpha2 * u
- self.alpha3**2 * sin_theta12 * cos_theta12 * theta1_dot**2
- self.alpha3 * self.alpha5 * ca.sin(theta2) * cos_theta12
- self.alpha3 * self.c2 * cos_theta12 * theta1_dot
+ self.alpha3 * self.c2 * cos_theta12 * theta2_dot
) / denominator
theta2_ddot = (
self.alpha1 * self.alpha3 * sin_theta12 * theta1_dot**2
+ self.alpha1 * self.alpha5 * ca.sin(theta2)
+ self.alpha1 * self.c2 * theta1_dot
- self.alpha1 * self.c2 * theta2_dot
+ self.alpha3**2 * sin_theta12 * cos_theta12 * theta2_dot**2
- self.alpha3 * self.alpha4 * ca.sin(theta1) * cos_theta12
+ self.alpha3 * self.c1 * cos_theta12 * theta1_dot
+ self.alpha3 * self.c2 * cos_theta12 * theta1_dot
- self.alpha3 * self.c2 * cos_theta12 * theta2_dot
- self.alpha3 * u * cos_theta12
) / denominator
dxdt = ca.vertcat(theta1_dot, theta1_ddot, theta2_dot, theta2_ddot)
return dxdt
def control(self, state, desired_state, t):
if (
self.last_update_time is None
or np.round(t - self.last_update_time, 2) >= self.dt
):
self.last_update_time = t
x0 = state
ref = desired_state
opti = ca.Opti()
U = opti.variable(self.N * self.nu)
x = ca.MX(x0)
cost = 0
for i in range(self.N):
u = U[i * self.nu : (i + 1) * self.nu]
x = self.predict_state(x, u, self.horizon_dt)
cost += ca.mtimes([(x - ref).T, self.Q, (x - ref)]) + ca.mtimes(
[u.T, self.R, u]
)
opti.minimize(cost)
for i in range(self.N * self.nu):
opti.subject_to(U[i] >= -300)
opti.subject_to(U[i] <= 300)
opts = {"ipopt.print_level": 0, "print_time": 0}
opti.solver("ipopt", opts)
try:
sol = opti.solve()
stats = sol.stats()
if stats["return_status"] == "Solve_Succeeded":
self.u = np.array(sol.value(U)[: self.nu]).flatten()
self.last_U = sol.value(U)
self.prev_u = self.u
else:
print(f"Optimization failed with status: {stats['return_status']}")
self.u = self.prev_u
except RuntimeError as e:
print(f"Optimization failed: {e}")
self.u = self.prev_u
return self.u
パラメタは以下のようにしました。
Q_mpc = np.diag([100, 1, 100, 1])
R_mpc = np.diag([0.01])
N = 10
horizon_dt = 0.1
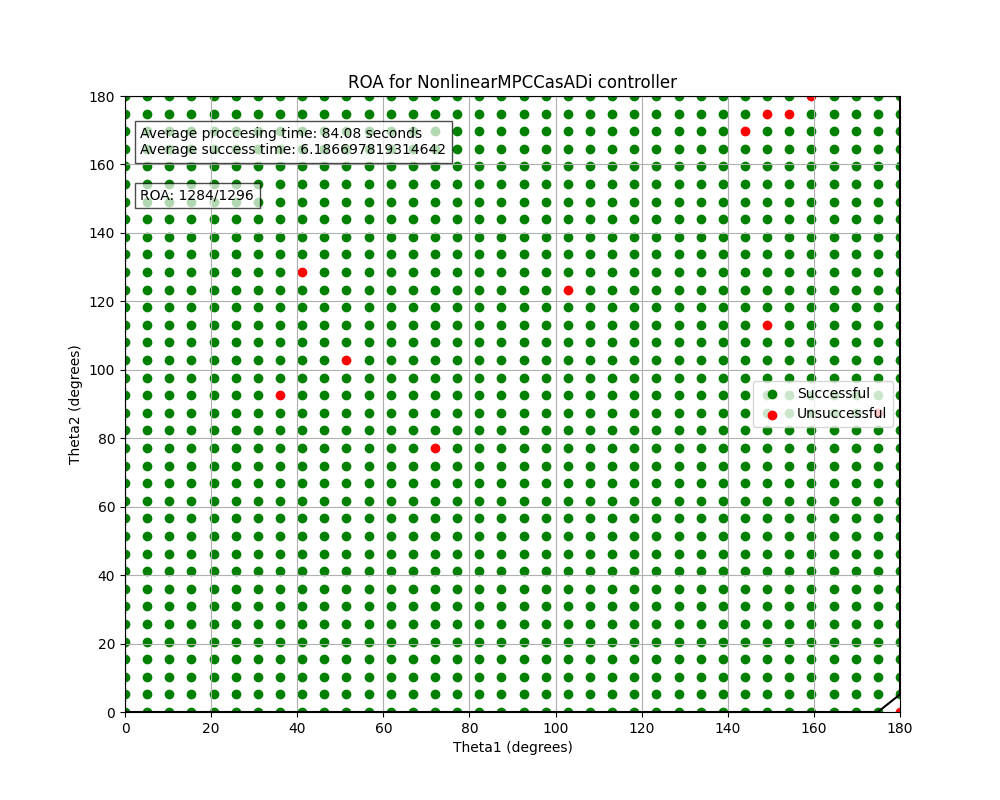
真下の状態
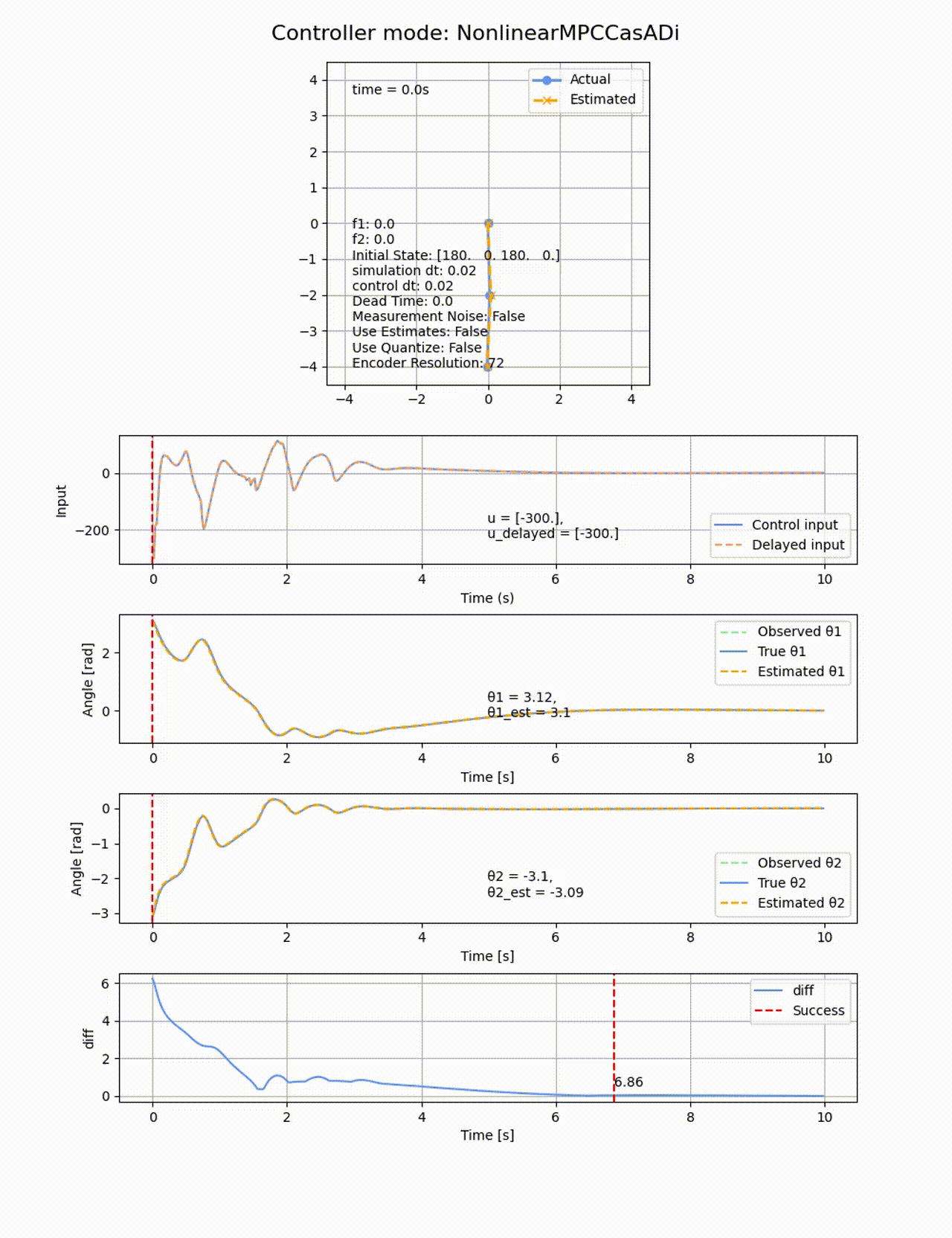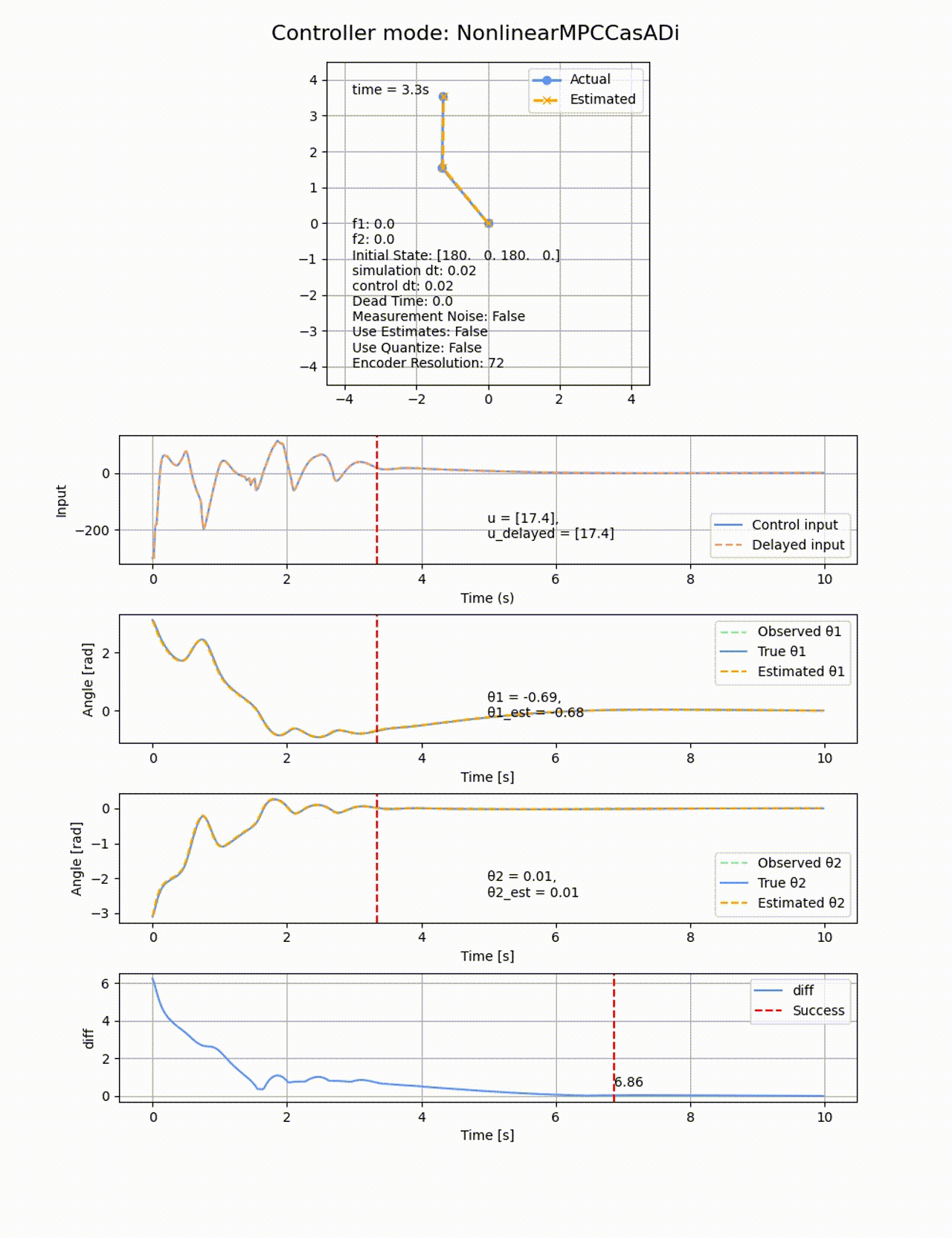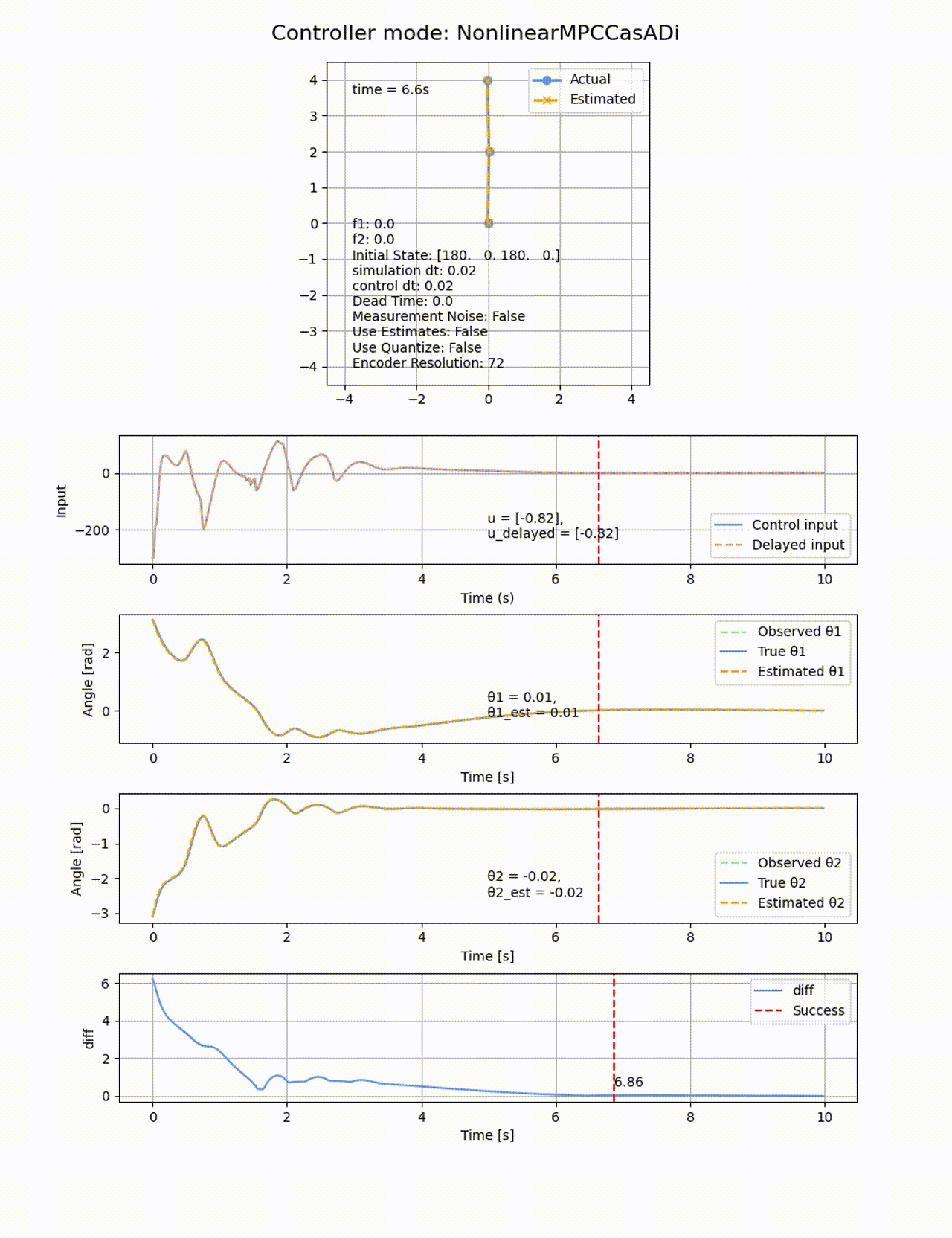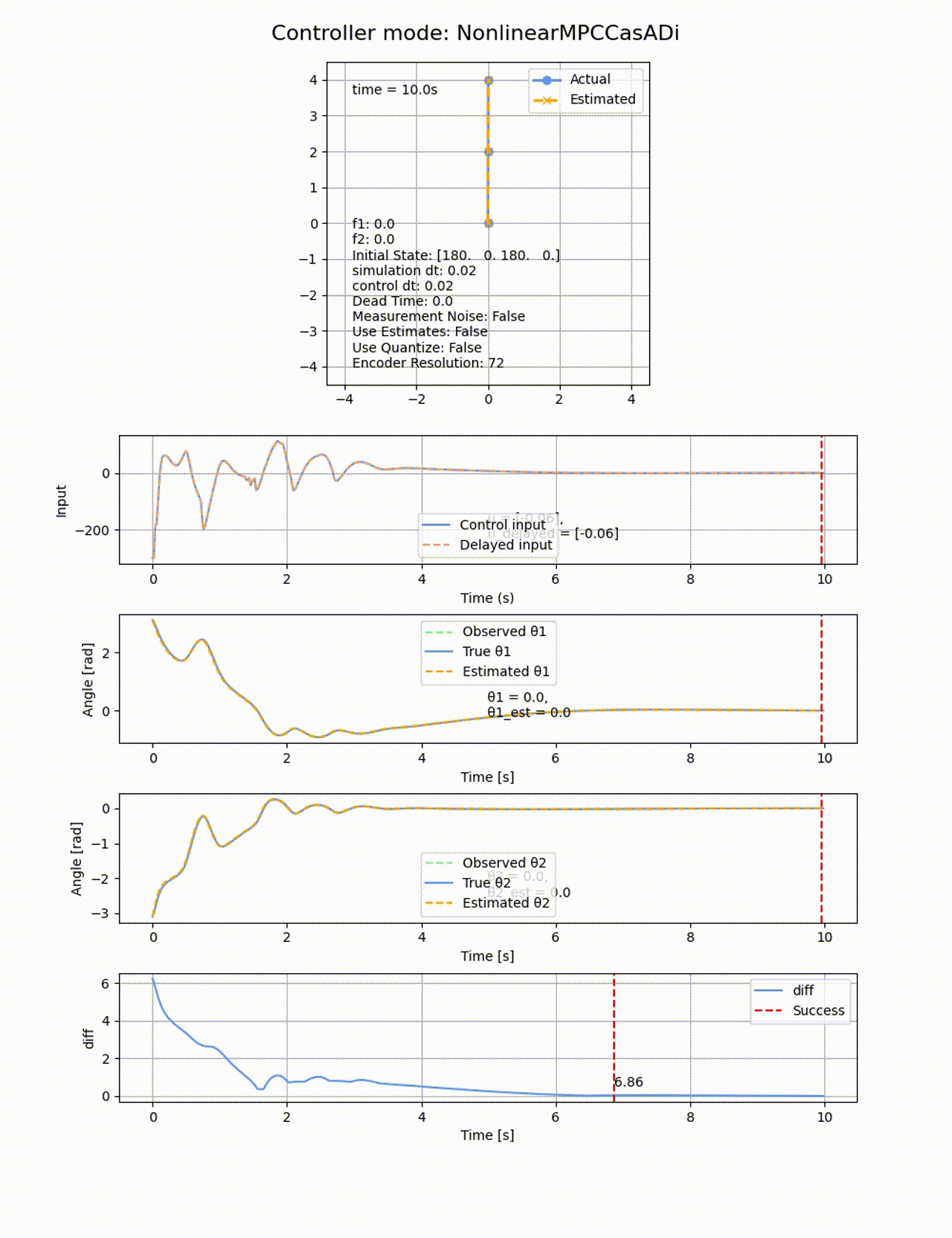
処理時間は84.08sと線形MPCよりも遅くなっています、ROAはもの凄く広くなり、ほぼ全ての初期値から倒立させることに成功しています。
比較表
以下に各制御器の比較表を示します。シミュレーション全体にかかる処理時間、倒立するまでの時間、成功した回数を示しています。ただし、それぞれ性能改善・処理時間改善の余地は多く残されているため、参考程度のまとめになります。
| 制御器 | 処理時間[s] | 成功時間[s] | ROA |
|---|---|---|---|
| PID | 0.33 | - | 1/1296 |
| Pole Placement | 0.32 | 5.664 | 44/1296 |
| LQR | 0.3 | 2.89 | 30/1296 |
| iLQR | 22.97 | 6.69 | 73/1296 |
| Linear MPC | 65.84 | 5.07 | 77/1296 |
| Nonlinear MPC | 84.08 | 6.18 | 1284/1296 |
計算時間がかかるものの非線形MPCが圧倒的に多くの初期値から倒立させることが出来ました。iLQRは非線形MPCよりは速く、比較的に多くの範囲での成功しています。極配置とLQRはこれらと比べるとかなり高速でした。
制御を難しくする
動摩擦
今度は2つのリンクに動摩擦を追加し、f1=0.3, f2=0.3とします。動摩擦は非連続の項になるため、微分による最適化ベースの制御であっても難しくなります。いずれの制御器であっても定常偏差が残ってしまいました。以下はLQRでの結果の例です
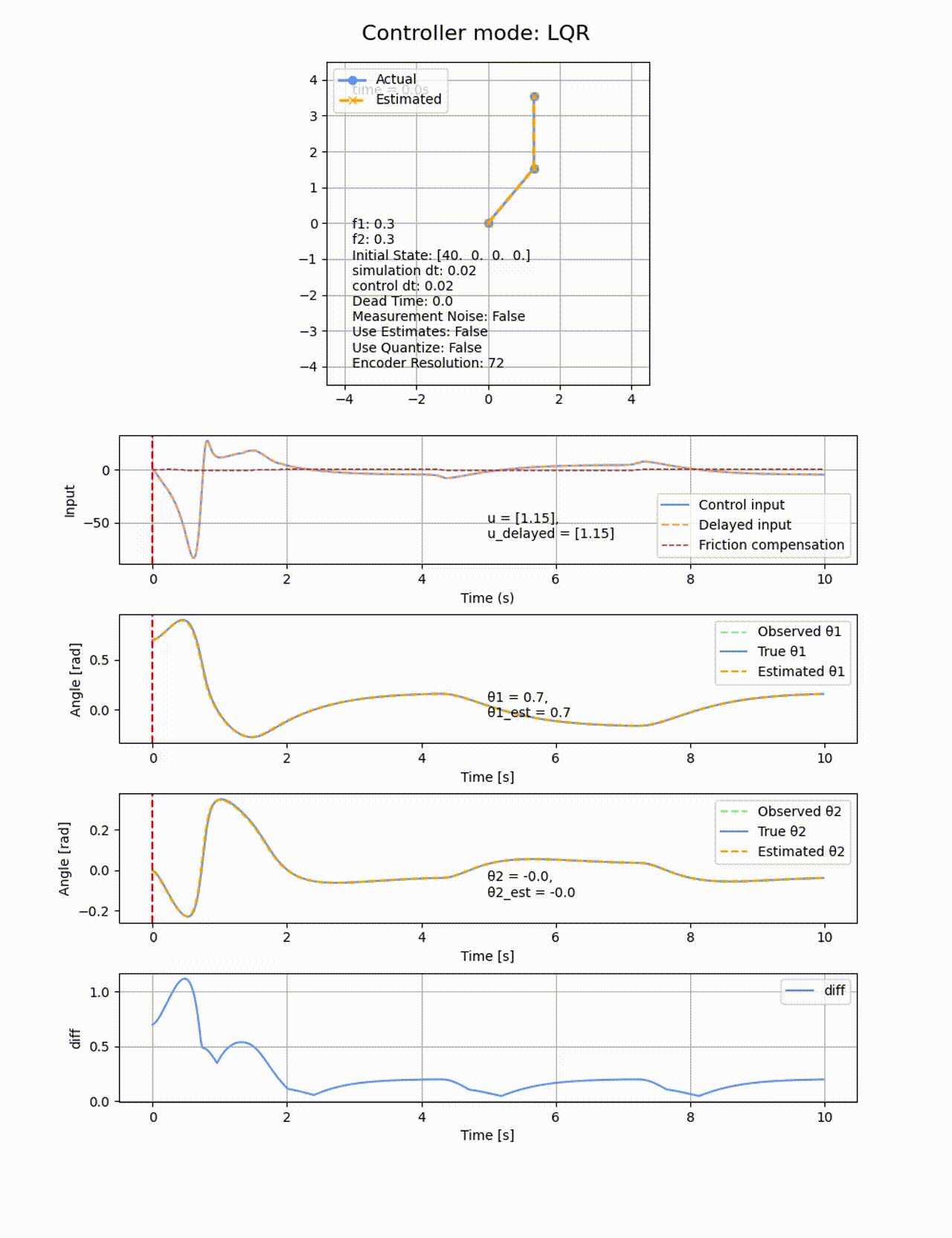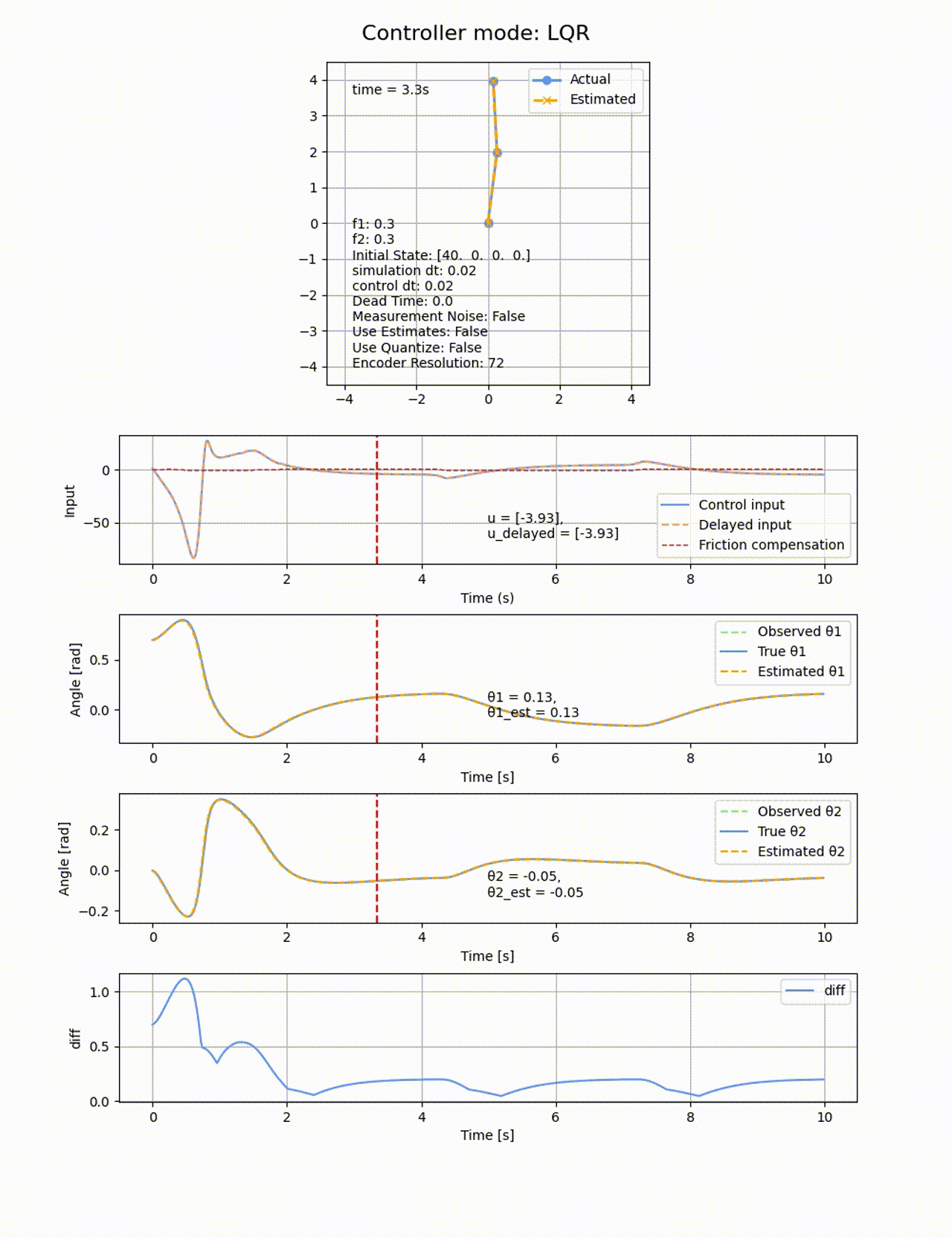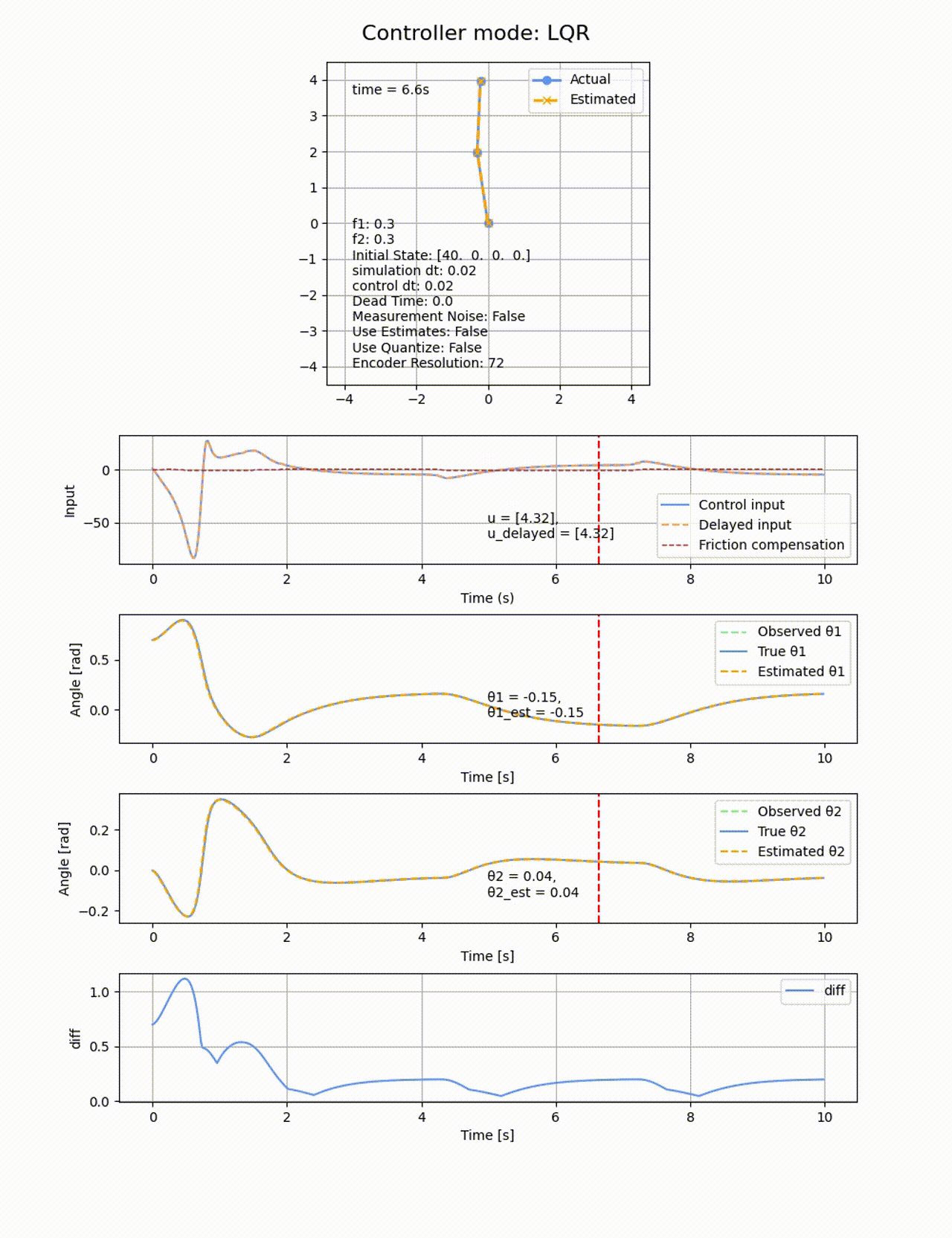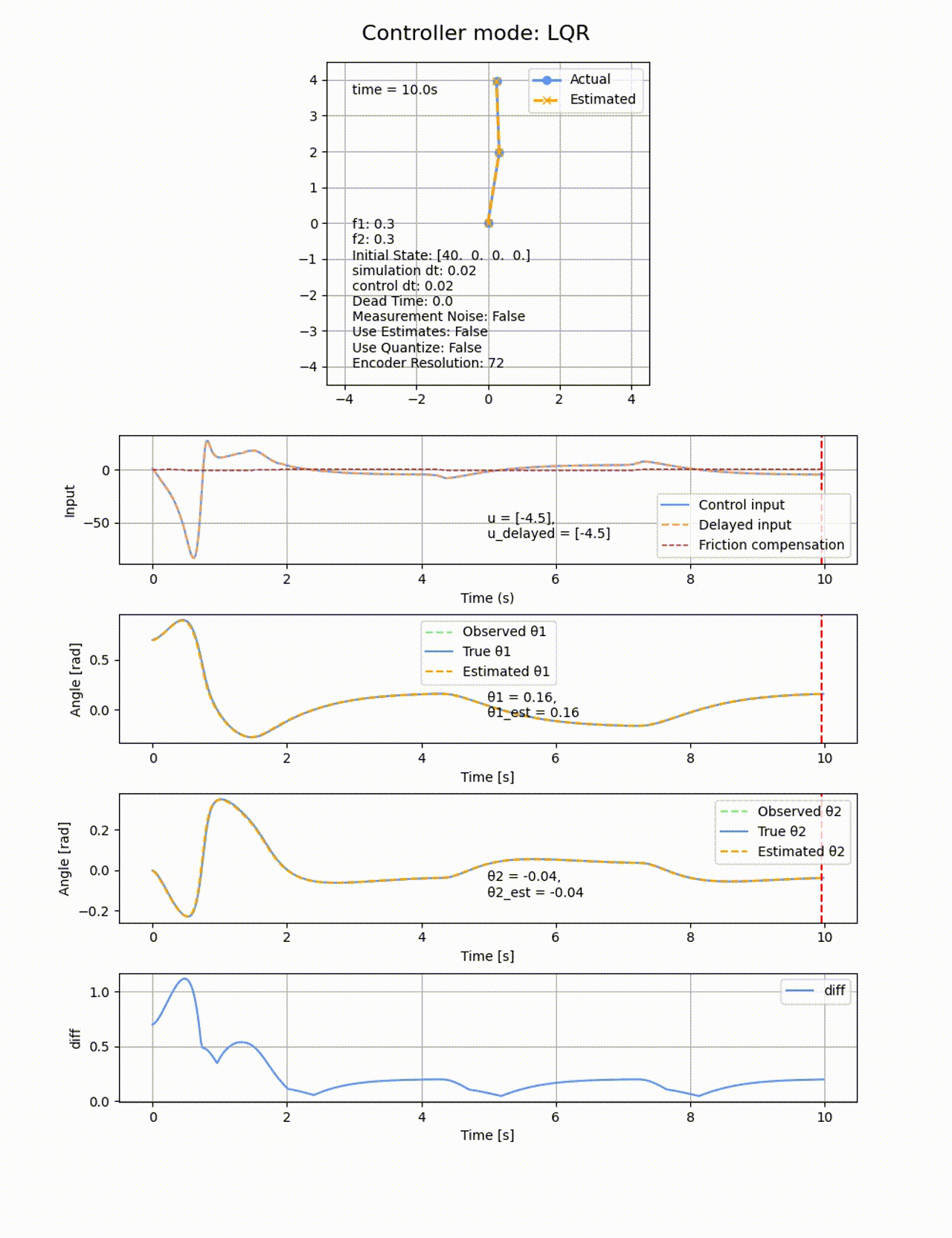
LQRに積分項を追加して、さらに動摩擦方向と逆向きに補正のための力を加えることで、動摩擦の影響を除けるか試してみます。
状態方程式を拡張して積分項を追加する方法は以下が参考になります
実装はこちらです。
class LQRControllerWithIntegral(Controller):
def __init__(self, A, B, C, Q, R, dt):
super().__init__(dt)
self.A_aug, self.B_aug, self.C_aug = self._augment_matrices(A, B, C)
self.K = self._calculate_lqr_gain(self.A_aug, self.B_aug, Q, R)
self.integral_error = np.zeros(1)
self.use_friction_compensation = True
self.f1 = 0.3
self.f2 = 0.3
self.friction_compensation = 0
self._friction_compensations = []
def _augment_matrices(self, A, B, C):
n = A.shape[0]
p = 1 # θ1, θ2のみの誤差を状態量に含めると可制御ではなくなるため、θ1のみの誤差を状態量に含める
A_aug = np.zeros((n + p, n + p))
A_aug[:n, :n] = A
A_aug[:n, n:] = np.zeros((n, p))
A_aug[n:, :n] = -np.array([[1, 0, 0, 0]])
B_aug = np.zeros((n + p, B.shape[1]))
B_aug[:n, :] = B
Wc = control.ctrb(A_aug, B_aug)
print(f"Wc: {Wc}")
if np.linalg.matrix_rank(Wc) != n + p:
print("System not Controllability\n")
else:
print("System Controllability\n")
C_aug = np.zeros((C.shape[0], C.shape[1] + p))
C_aug[:, : C.shape[1]] = C
return A_aug, B_aug, C_aug
def _calculate_lqr_gain(self, A, B, Q, R):
X = solve_continuous_are(A, B, Q, R)
K = inv(R) @ B.T @ X
return K
def control(self, state, desired_state, t):
if (
self.last_update_time is None
or np.round(t - self.last_update_time, 2) >= self.dt
):
self.last_update_time = t
error = desired_state[0] - state[0] # θ1の誤差のみを積分
self.integral_error += error * self.dt
augmented_state = np.hstack((state - desired_state, self.integral_error))
self.u = -self.K @ augmented_state
if self.use_friction_compensation:
self.friction_compensation = (
self.f1 * sign(state[1]) + self.f2 * sign(state[1] + state[3])
) * 1
self.u += self.friction_compensation
if self.use_friction_compensation:
self._friction_compensations.append(self.friction_compensation)
return self.u
def get_friction_compensations(self):
return self._friction_compensations
ここで、Wc = control.ctrb(A_aug, B_aug)で計算でき、そのランクが np.linalg.matrix_rank(Wc) != n + p:によってシステムの状態変数の数に等しいか確認しています。可制御性はシステムがある状態から別の望ましい状態へ遷移させることが可能かどうかを示す指標です。
積分項を追加した場合、確かに一定時間経過すると定常偏差を無くす方向に制御が働きますが、オーバシュートしてしまいます。ぴったり倒立させることは難しいです。
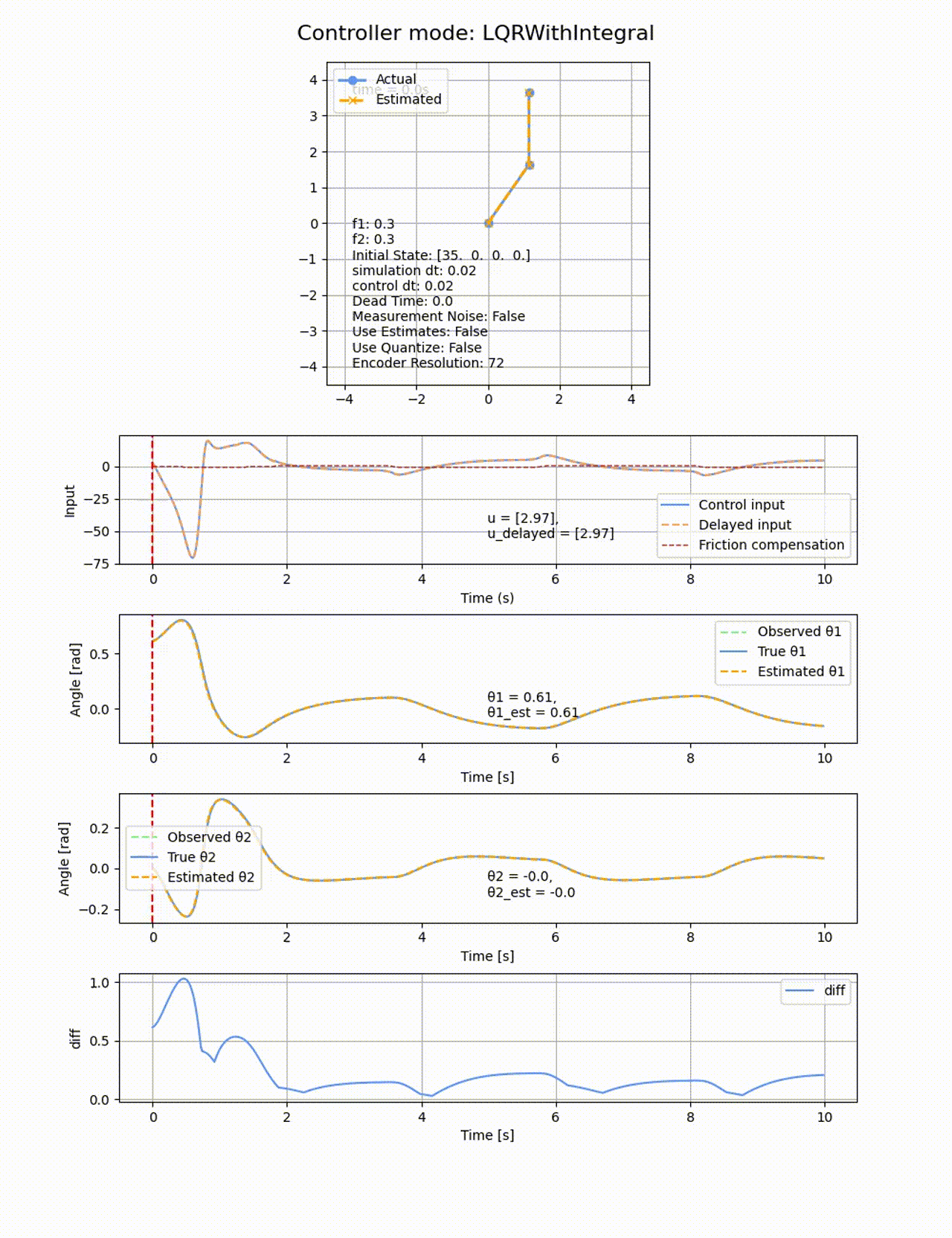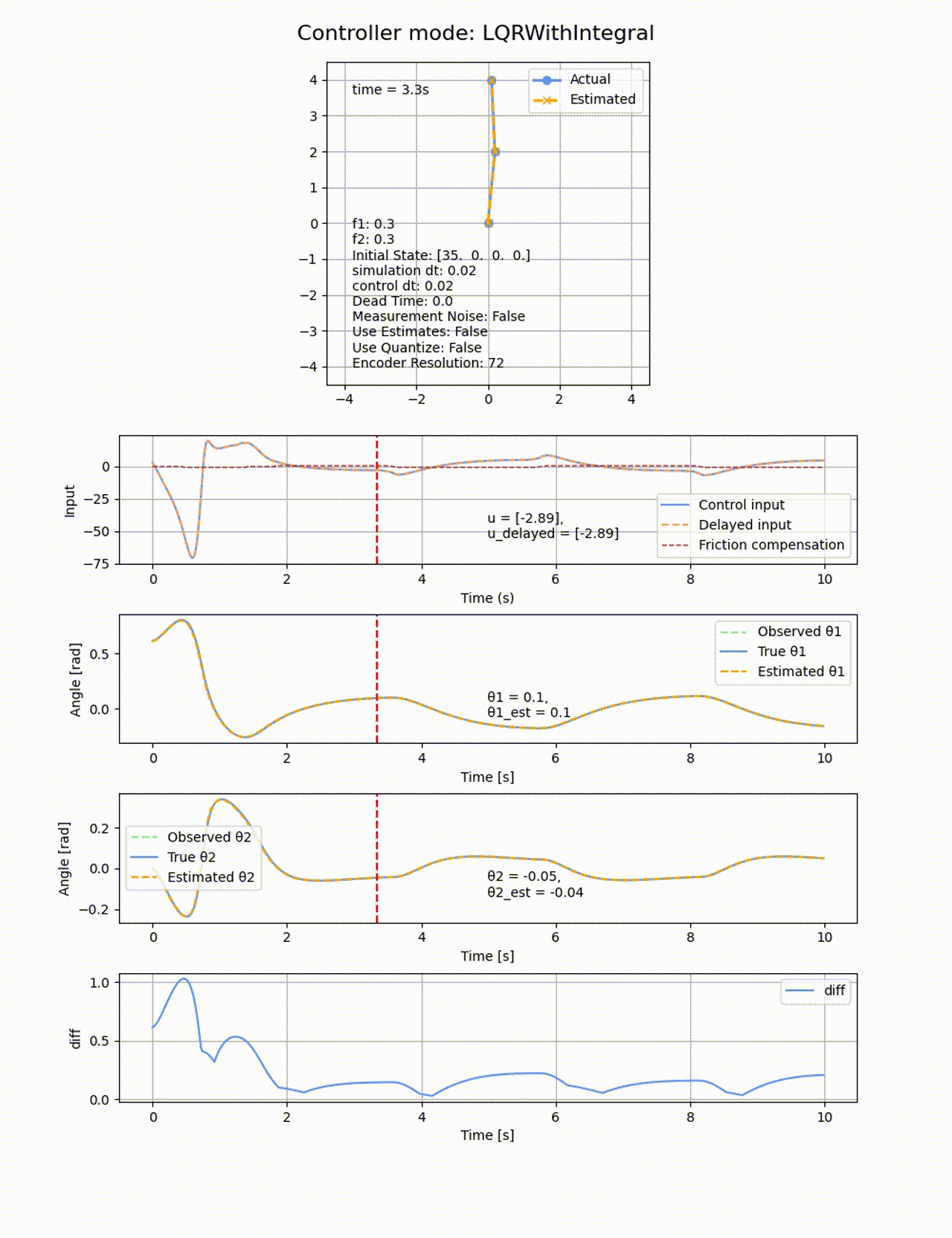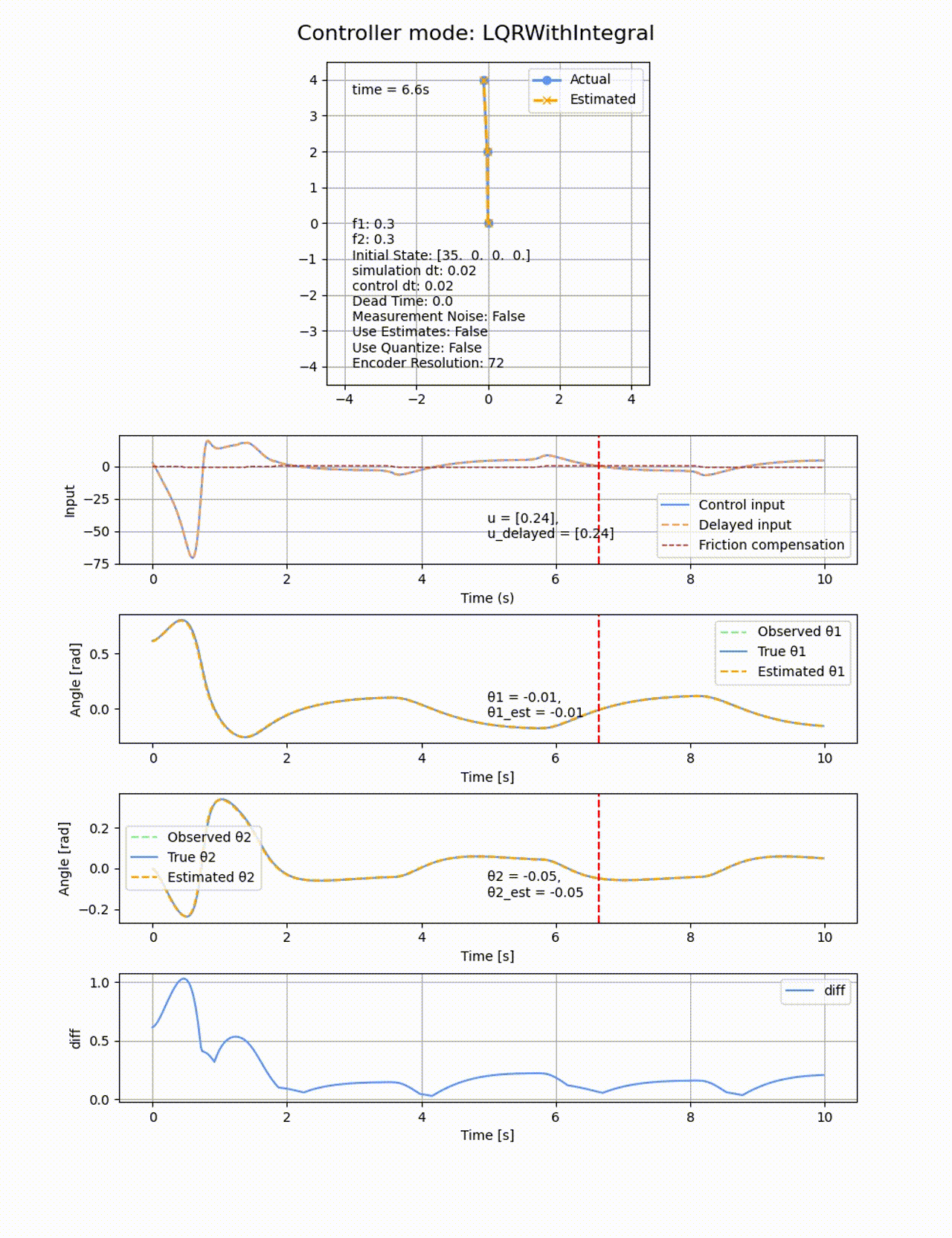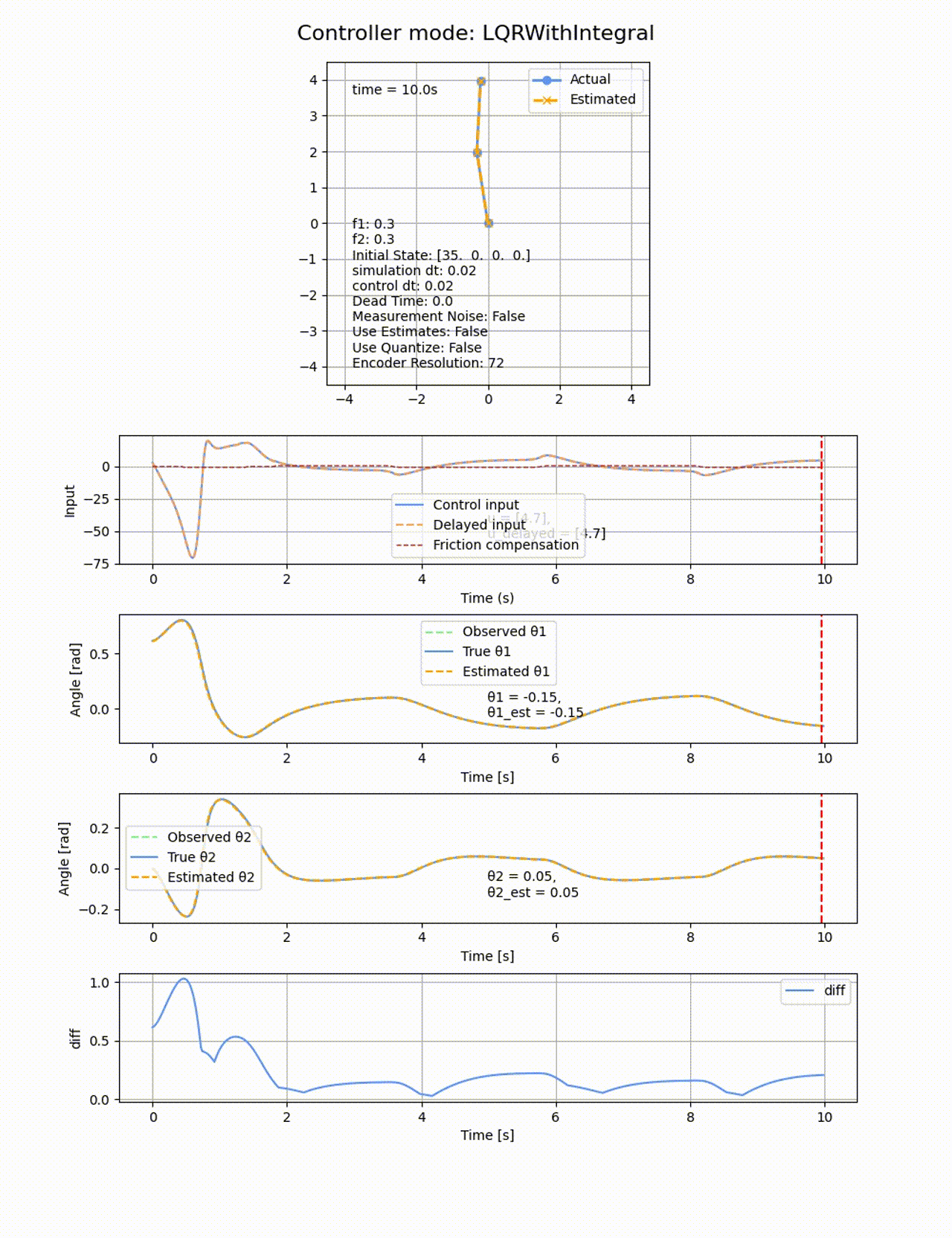
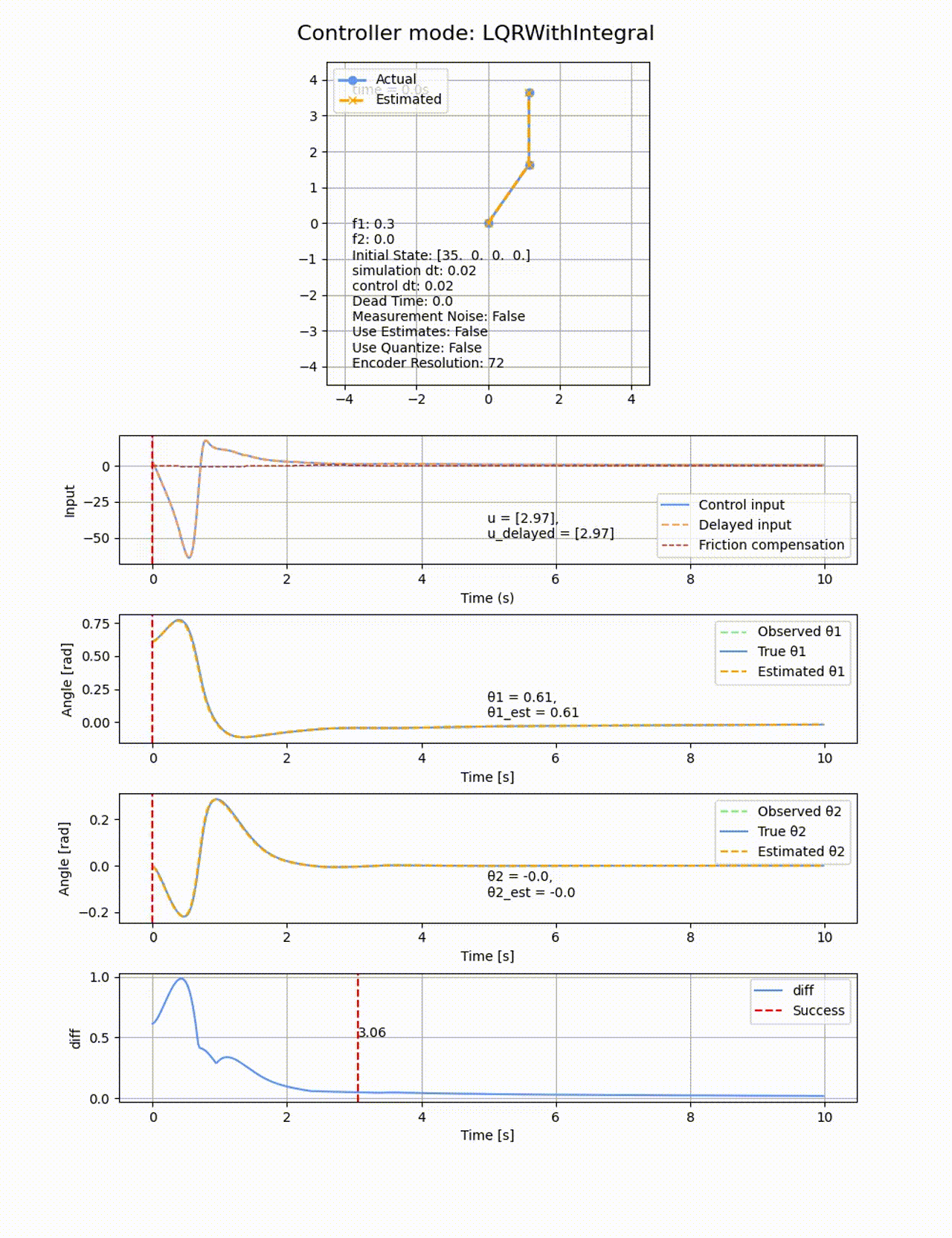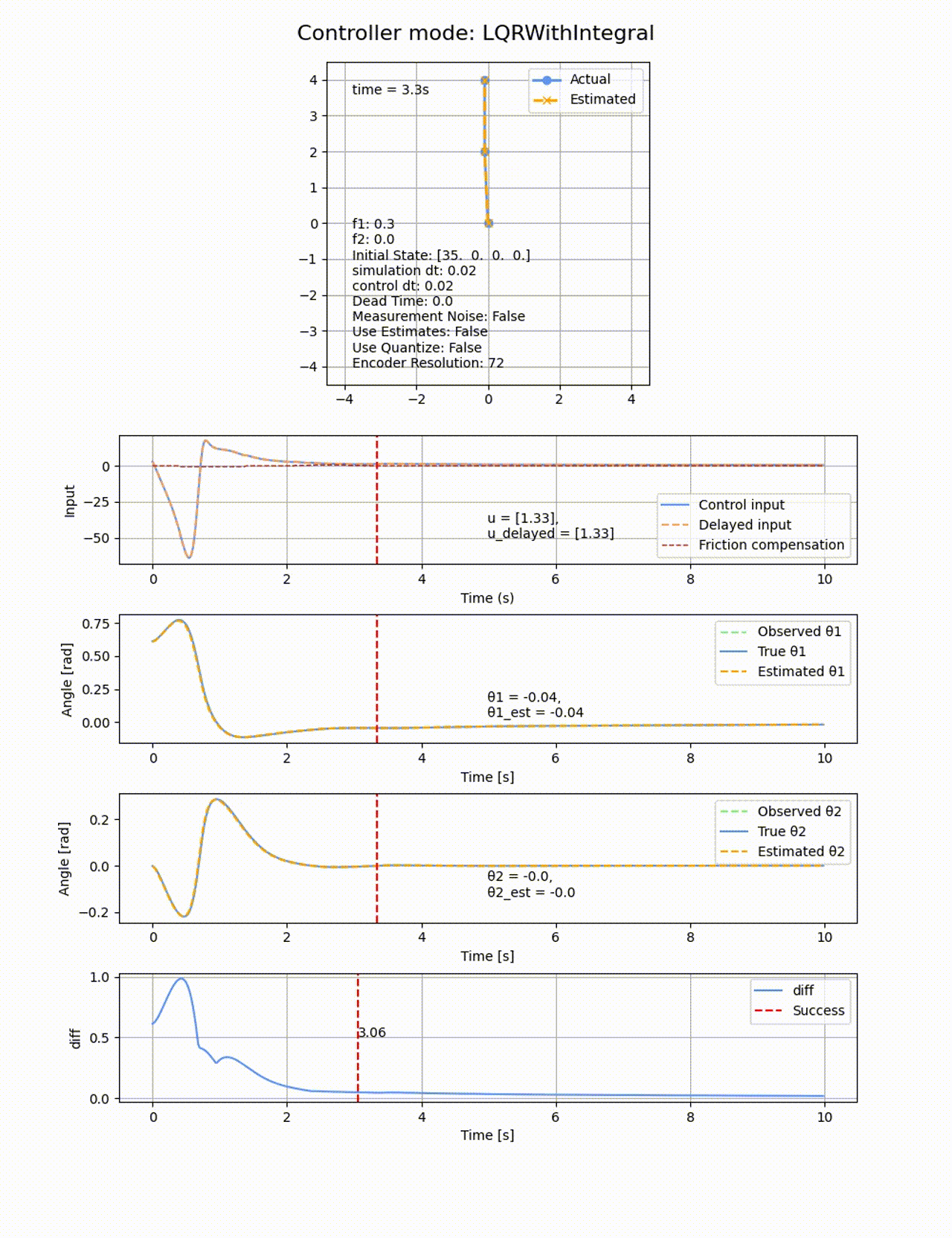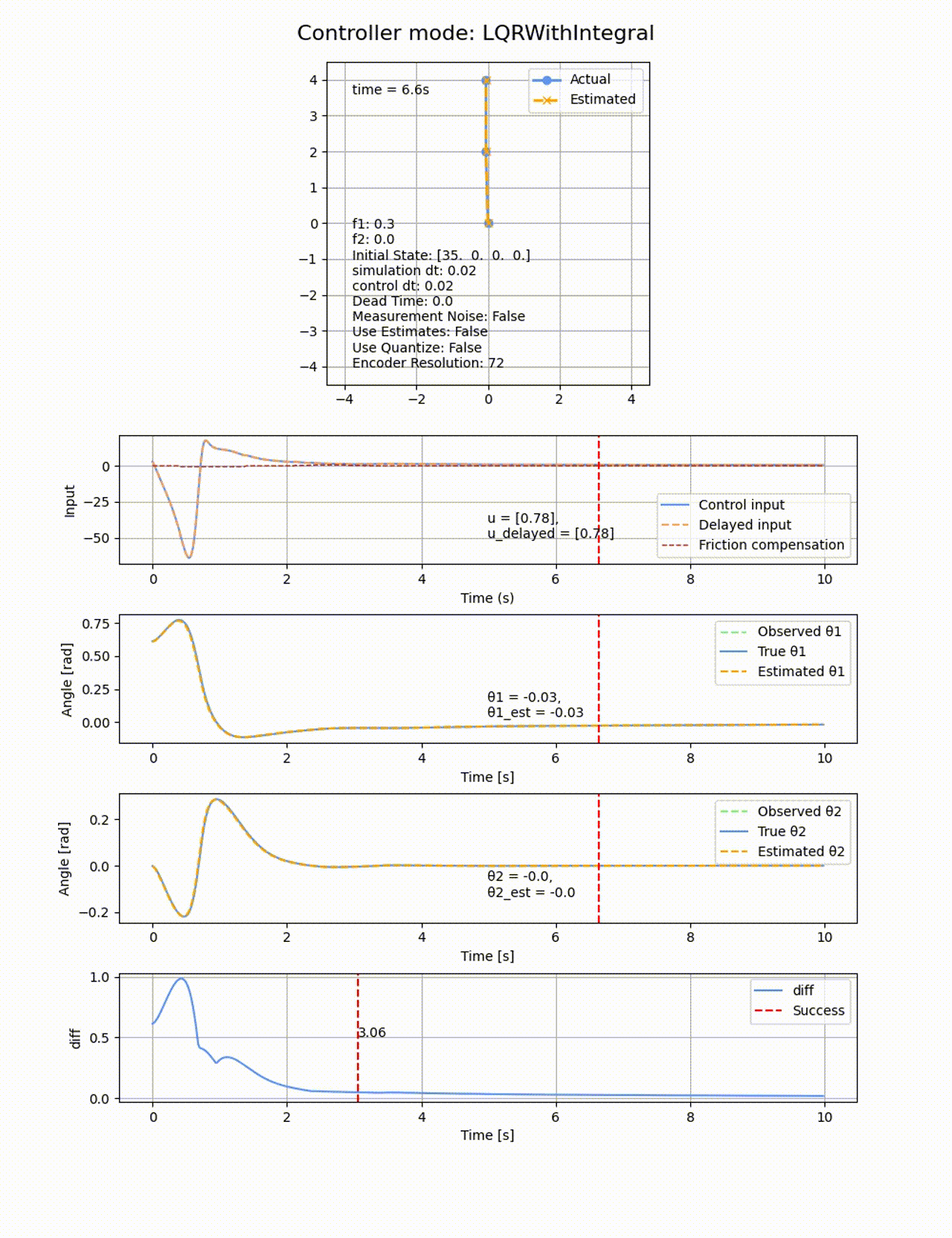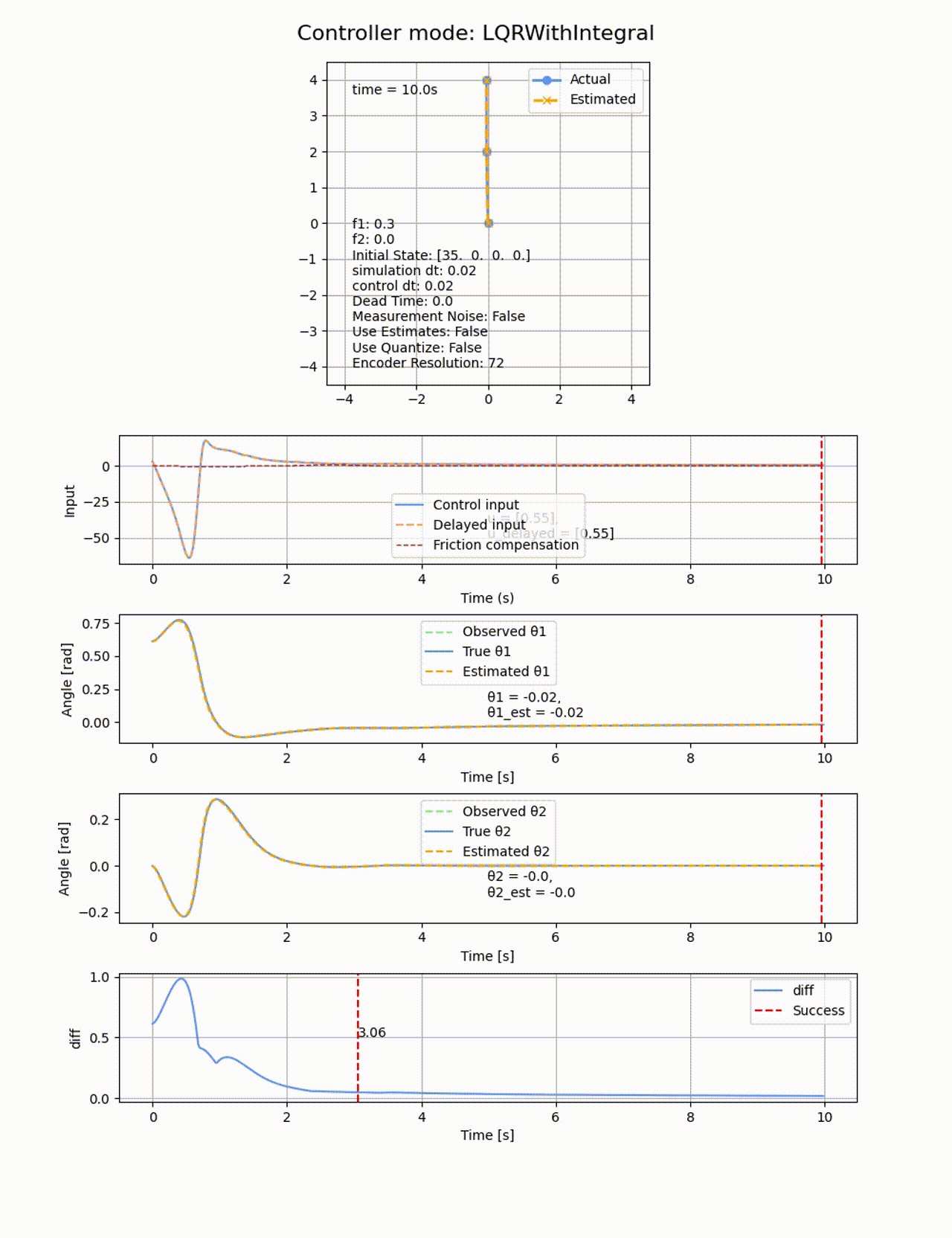
2つ目のリンクの動摩擦係数f2=0にすると上手く収束するので、非駆動のリンクに動摩擦があることが難易度が上がることが分かります。
遅延
制御入力に無駄時間を追加してみます。0.02sの制御周期に対して、0.05sの遅延を追加します。LQRで制御を行ったところ、ちょっとプルプルしましたが、
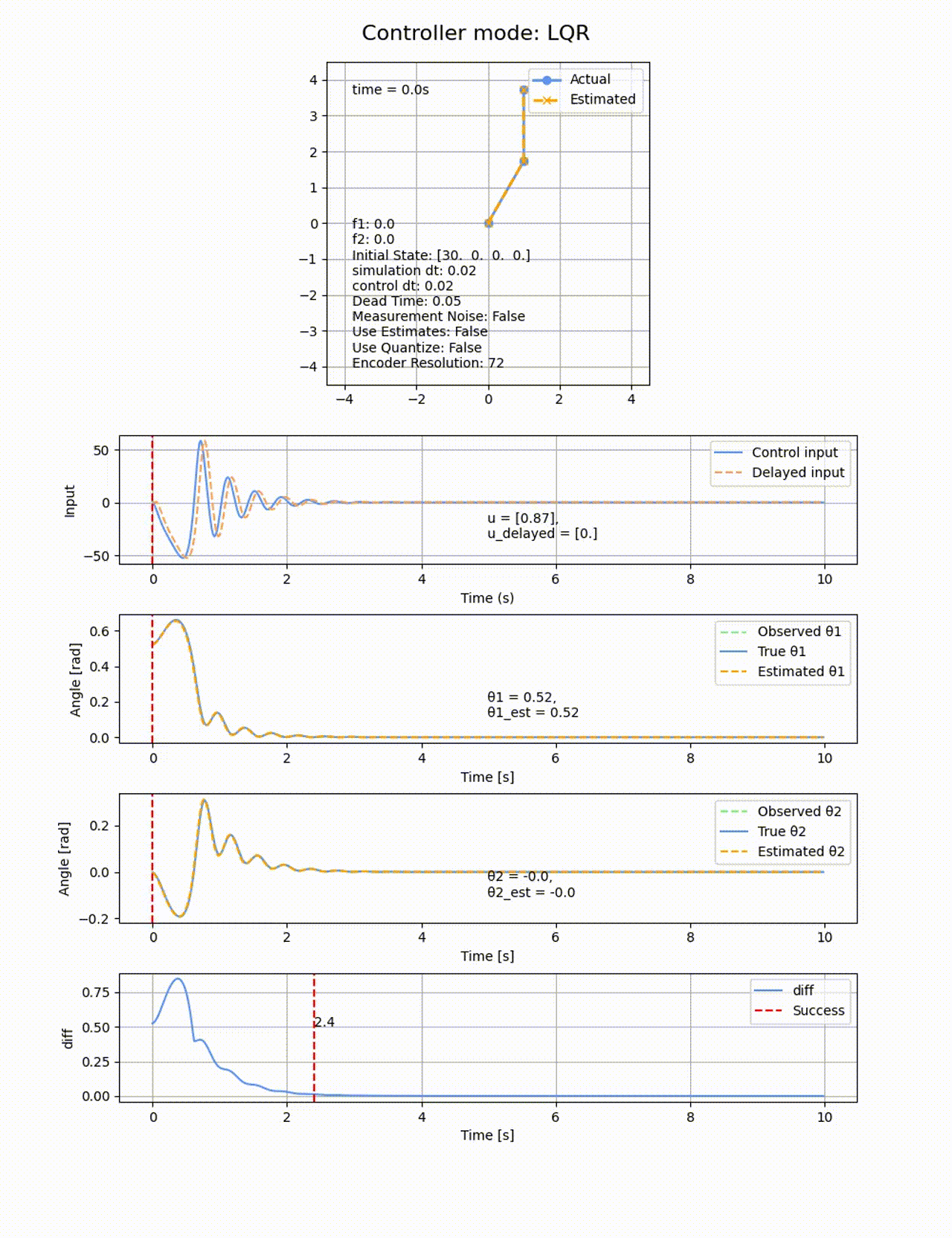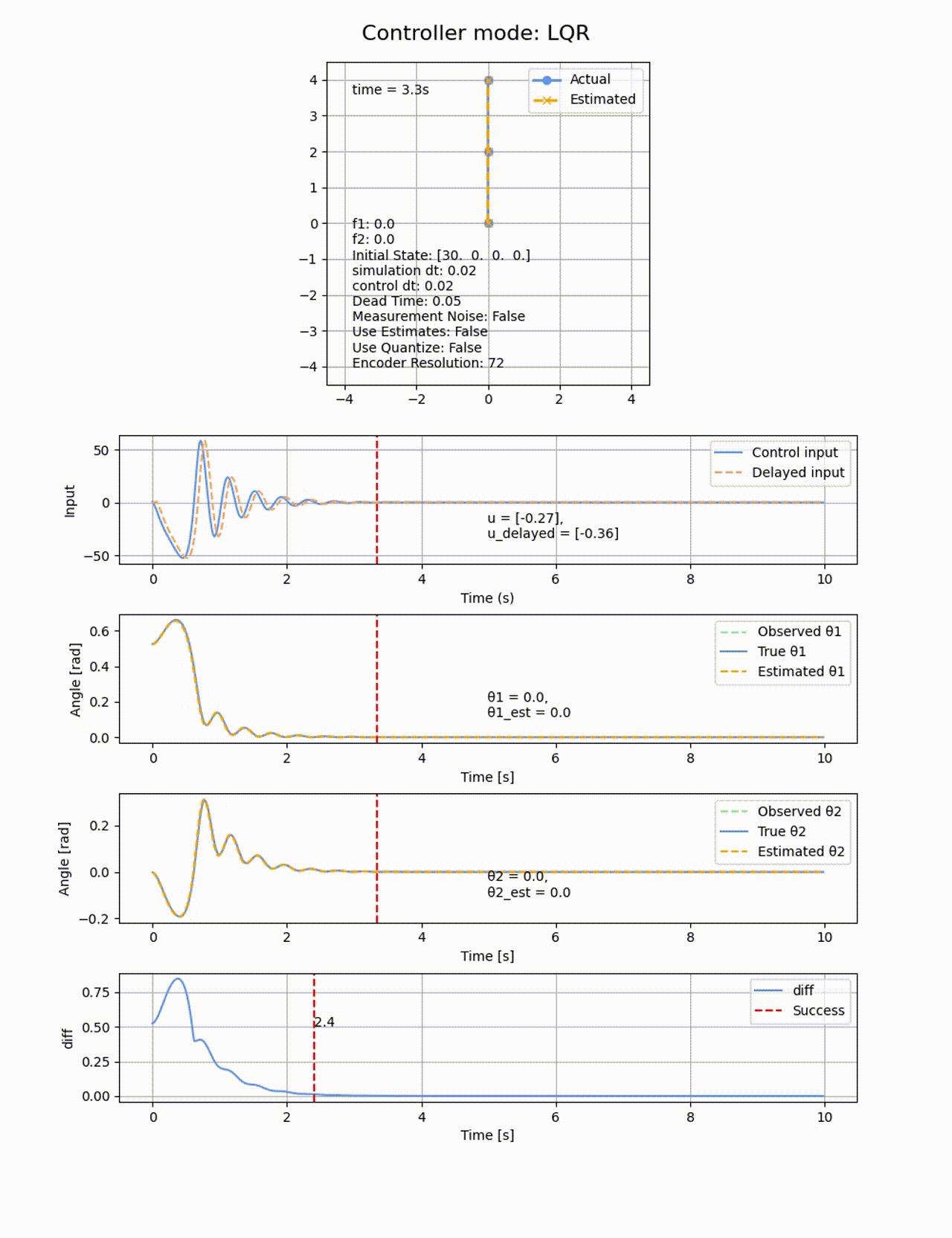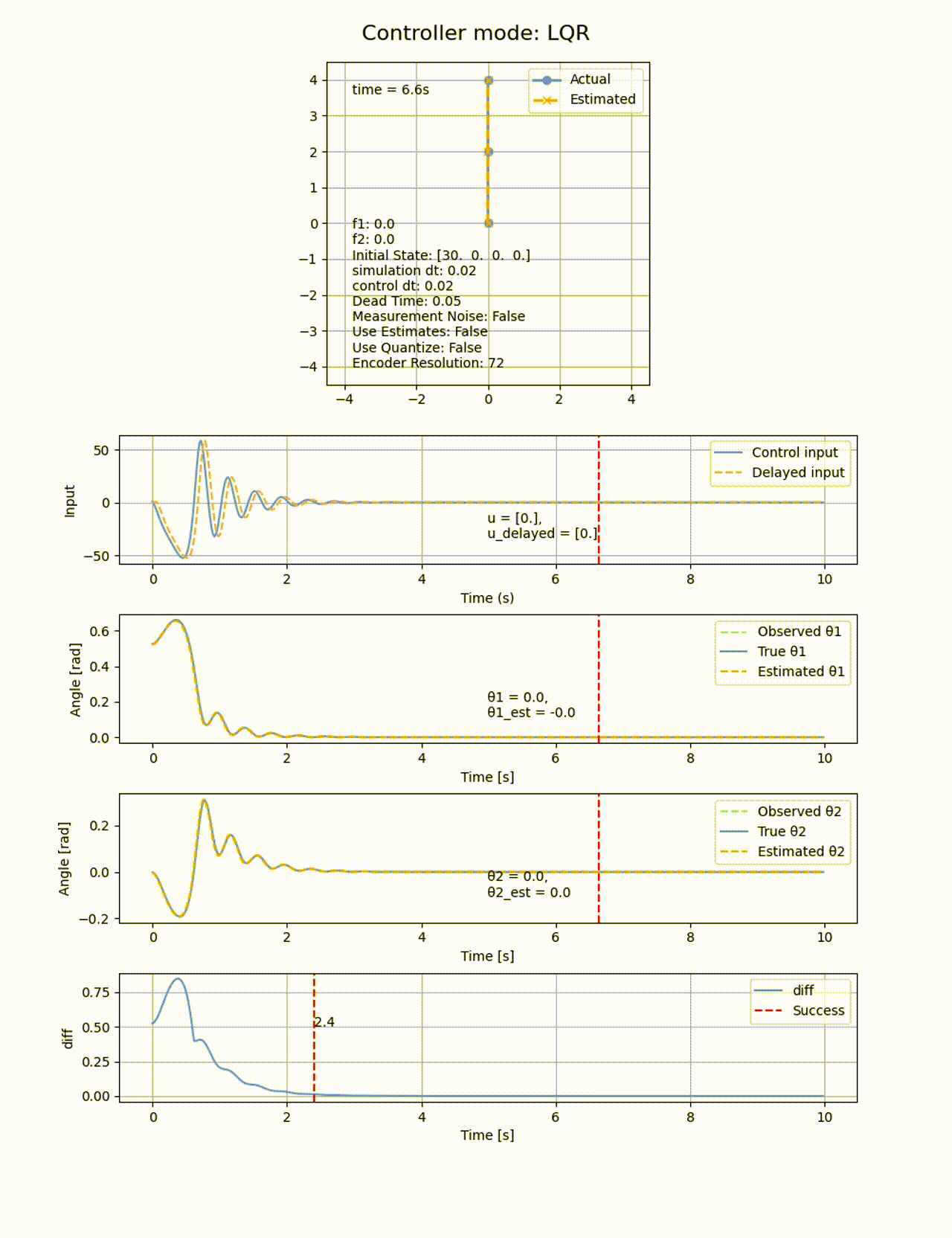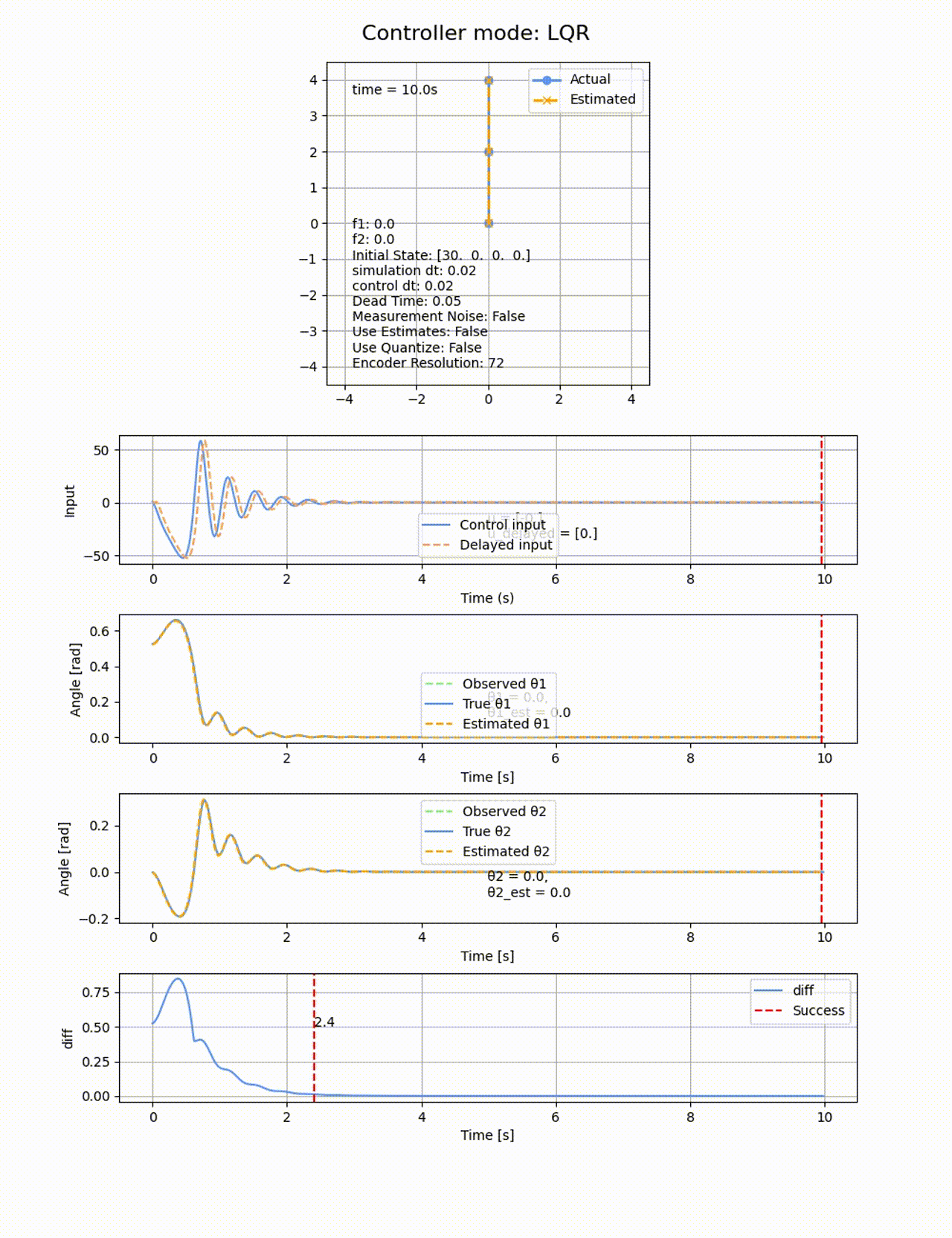
遅延がないのときのROA

遅延0.05sのときのROA:縮小していることが分かります。

遅延0.1sのときのROA:全滅です

遅延への対応はスミス予測器というものが有名です。
参考文献
- 倒立振子で学ぶ制御工学 (川田 昌克, 東 俊一, 市原 裕之, 浦久保 孝光, 大塚 敏之, 2017)
- PythonとCasADiで学ぶモデル予測制御 (深津 卓弥, 菱沼 徹, 荒牧 大輔)
- Pythonによる車輪形倒立振子の運動方程式の導出
- Pythonによる台車形倒立振子のシミュレーション
- Pythonによる車輪形倒立振子の線形化と最適レギュレータ
- Pythonによる台車形倒立振子の線形化と最適レギュレータ
- 線形最適制御(LQR)とRiccatiソルバーについて
- 凸最適化の概要と主双対内点法のアルゴリズムの解説
- iLQR全解説-基礎理論編-
- LQR/iLQRを理解する
- iLQRによる差動二輪車の非線形モデル予測制御
- モデル予測制御(MPC)による軌道追従制御
Discussion