本記事の内容
本記事では以下の内容について解説します。
テブナンの定理による等価回路の作り方
テブナンの定理は簡潔に言うと、「回路上の任意の2端子を選んだ時、その間の開放電圧、内部抵抗を用いて等価電圧源を構成できる」 というものです。
回路図を用いて説明します。下図のように、内部に電圧源や電流源を含む回路網を N_0、含まない回路網を N とします。
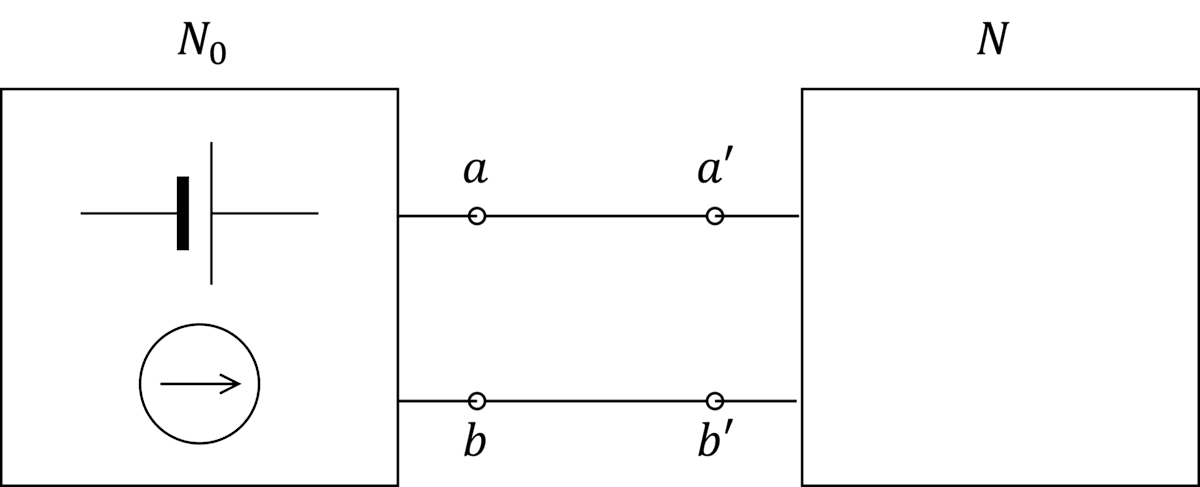
回路網 N_0 の電圧源を短絡、電流源を開放したときの開放インピーダンスを R_0、 端子 a,b 間を開放したときの N_0 の開放電圧を V_0 とおきます。

このとき、回路網 N_0 は電圧 V_0 の理想電圧源と内部抵抗 R_0で構成される電圧源と等価になります。

回路網 N に電圧源あるいは電流源を含む場合も等価電圧源の作り方は同じで、等価電圧源に回路網 Nを接続すれば、変換前の回路と同じ動作になります。

ちなみに、回路全体に複数の電源がある場合は、重ね合わせの原理を用いることで解析することができます。
例題
テブナンの定理を使った問題を2題示します。
例題1
下図の回路の抵抗 R_4 に流れる電流を求めてみましょう。

端子 a,b を開放したときの開放電圧 V_0 は次式で与えられます。
V_0 = \frac{R_2}{R_1+R_2} E
開放インピーダンス R_0 は、電圧源を短絡することで、次式で与えられます。
R_0 = \frac{R_1 R_2}{R_1+R_2} + R_3

したがって、等価回路は下図のようになります。

抵抗 R_4 に流れる電流 I は、開放電圧 V_0 と開放インピーダンス R_0 を用いて次式で表されます。
例題2
下図の回路の抵抗 R_4 に流れる電流を求めてみましょう。

端子 a,b の左側の等価回路については例題1と全く同様になります。

端子 a,b の右側に電圧源 E_2 が接続されているため、重ね合わせの原理を適用することで、抵抗 R_4 に流れる電流 I が次式で与えられます。
I = \frac{V_0-E_2}{R_0 + R_4}
テブナンの定理の証明
本節では、テブナンの定理の証明を行います。
回路網Nに電源を含まない場合
テブナンの定理の証明には、重ね合わせの原理を用います。内部に電圧源や電流源を含む回路網を N_0、含まない回路を N とし、端子 a,b で接続されているとします。

回路網 N_0 の開放電圧を V_0 とします。

ここで、端子 a,a' 間と端子 b,b' 間に電圧 V_0 の電圧源を置いた回路を考えてみます。

回路網 N の端子 a', b' の電圧は V_0 ずつ上がりますが、端子間の電圧 V は変化しないため、回路網 N に流れる電流 I も変化しません。したがって、 端子 a,a' 間と端子 b,b' 間に電圧 V_0 の電圧源を置いた回路は、元の回路と同じ動作になります。
この回路について、下図のように重ね合わせの原理を適用します。

左側の回路は端子 a, a' 間の電圧源を短絡したもの、右側の回路は他のすべての電圧源・電流源を短絡・開放したものです。左側の回路について、端子 a', b' 間の電圧は、N_0 の開放電圧が V_0 だったことから、0\,\mathrm{V} となります。そのため、回路網 N には電流が流れません。したがって、重ね合わせの原理より、右側の回路の回路網 N に流れる電流および発生する電圧は、元の回路のそれと等しくなります。右側の回路は、回路網 N_0 の電圧源・電流源を短絡・開放し、端子 a に開放電圧を接続したものですから、テブナンの等価回路そのものです。
以上で、テブナンの等価回路の証明が完了しました。
回路網Nに電源を含む場合
先の証明では、回路網 N に電源を含まない場合を考えましたが、電源を含む場合はどうなるでしょうか。実は、重ね合わせの原理で分解した一個目の回路において、回路網 N の電圧源を短絡、電流源を開放して考えることで、同様の議論が成立します。

左側の回路について、回路網 N_0 の開放電圧 V_0 が端子 b 側に接続されていることに加え、回路網 N の内部には電源がない状態なので、端子 a', b' は等電位です。よって、回路網 N に電源が含まれない場合と同じく、回路網 N に流れる電流は 0\,\mathrm{A} となります。
したがって、回路網 N に電源を含まない場合の証明と同様に、左側の回路がテブナンの等価回路に相当します。
参考文献
- 榊米一郎・大野克郎・尾崎弘(1980)『大学課程電気回路(1) (第2版)』オーム社














Discussion