本記事の内容
本記事では、交流信号の表現方法であるフェーザについて解説します。
- フェーザ表示、フェーザ図
- インピーダンス
- 交流RLC回路
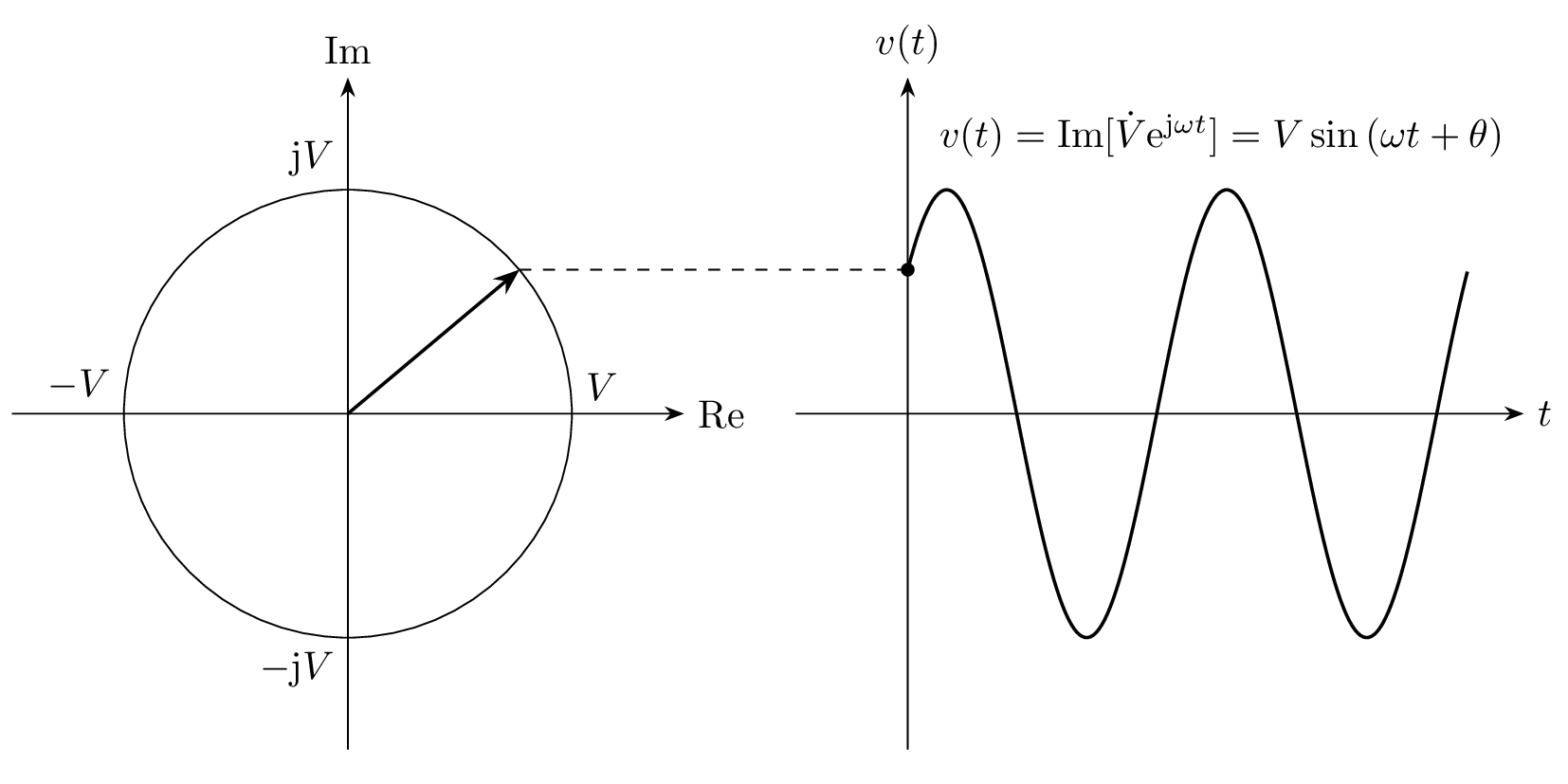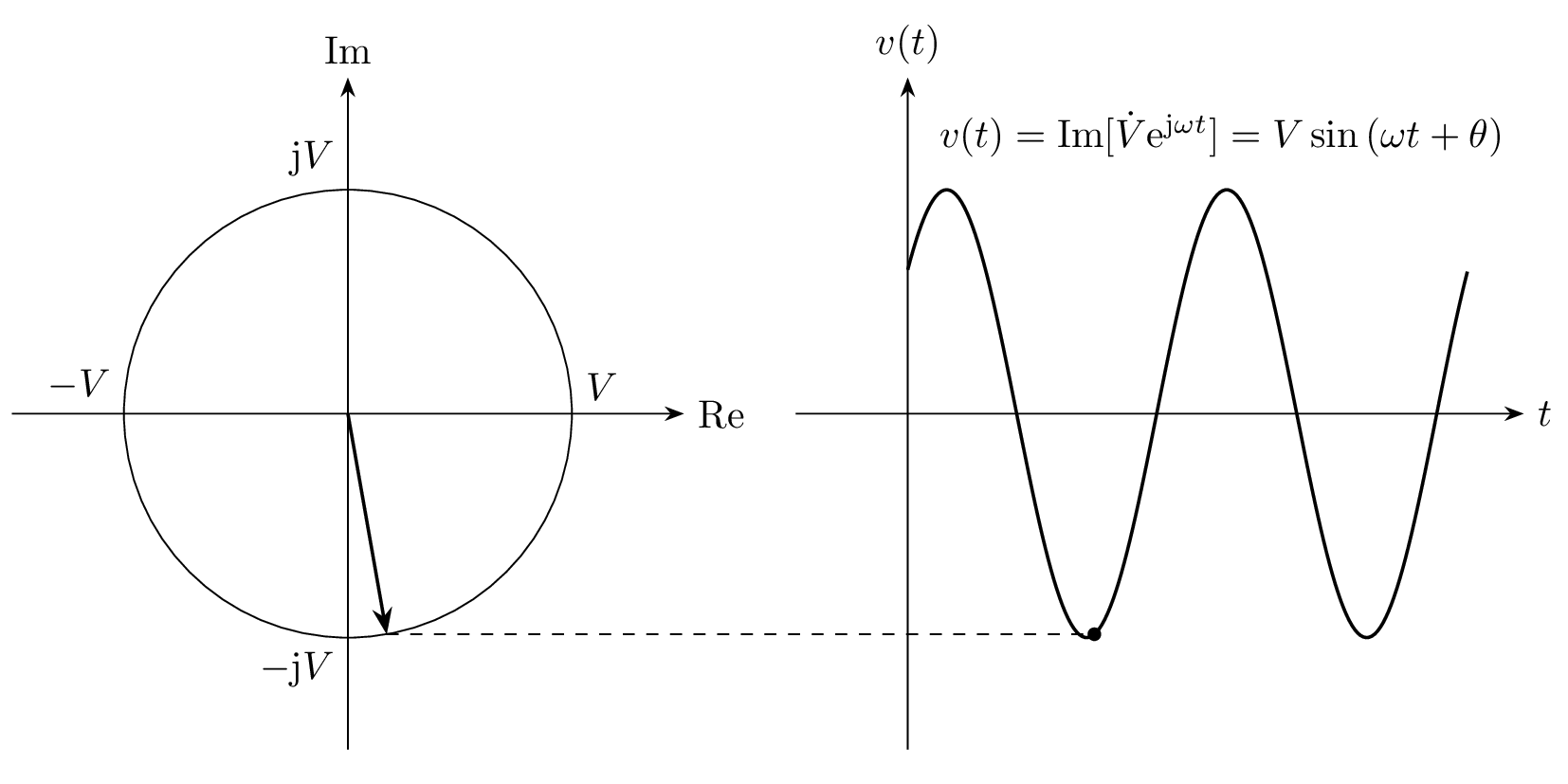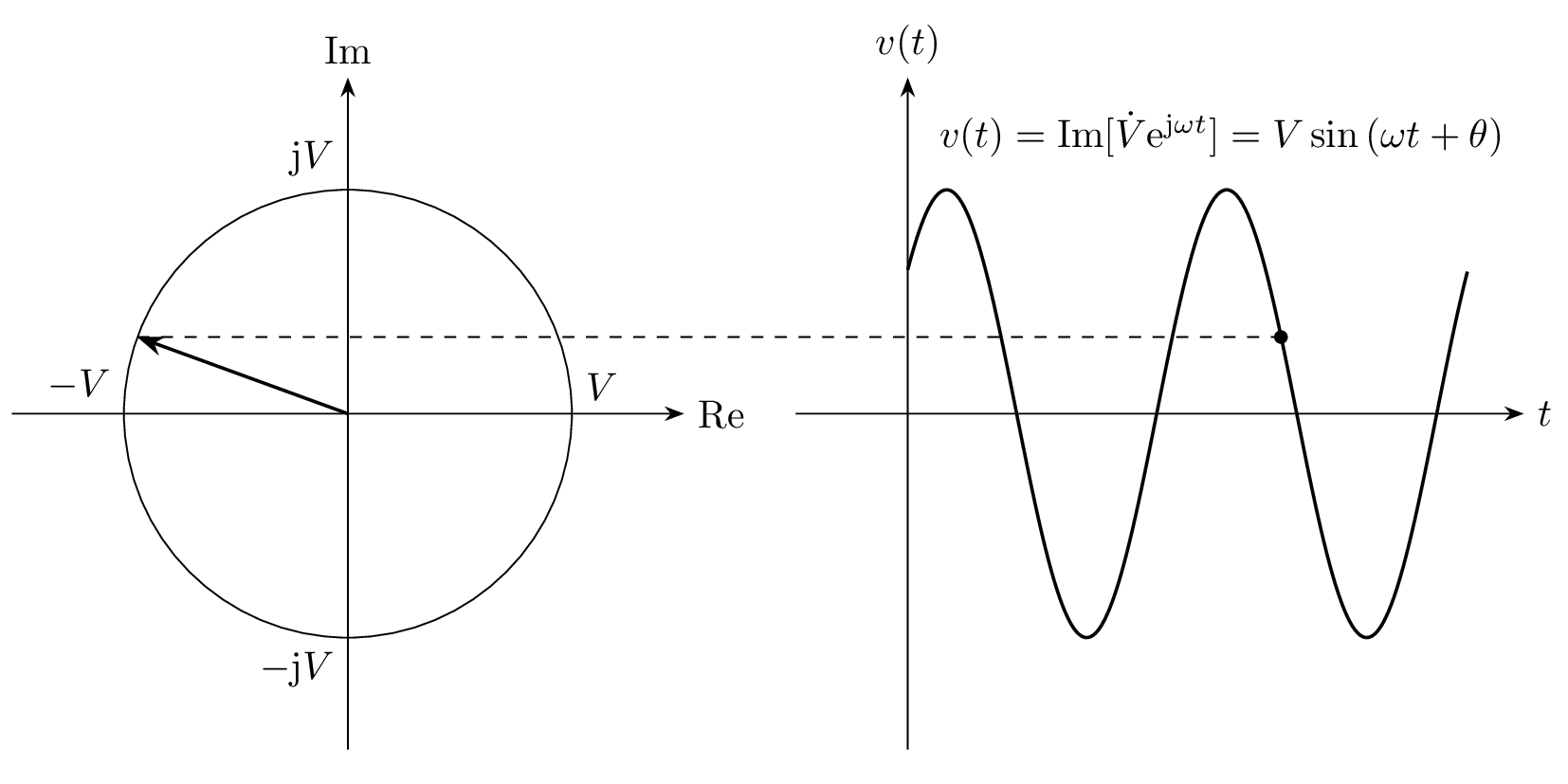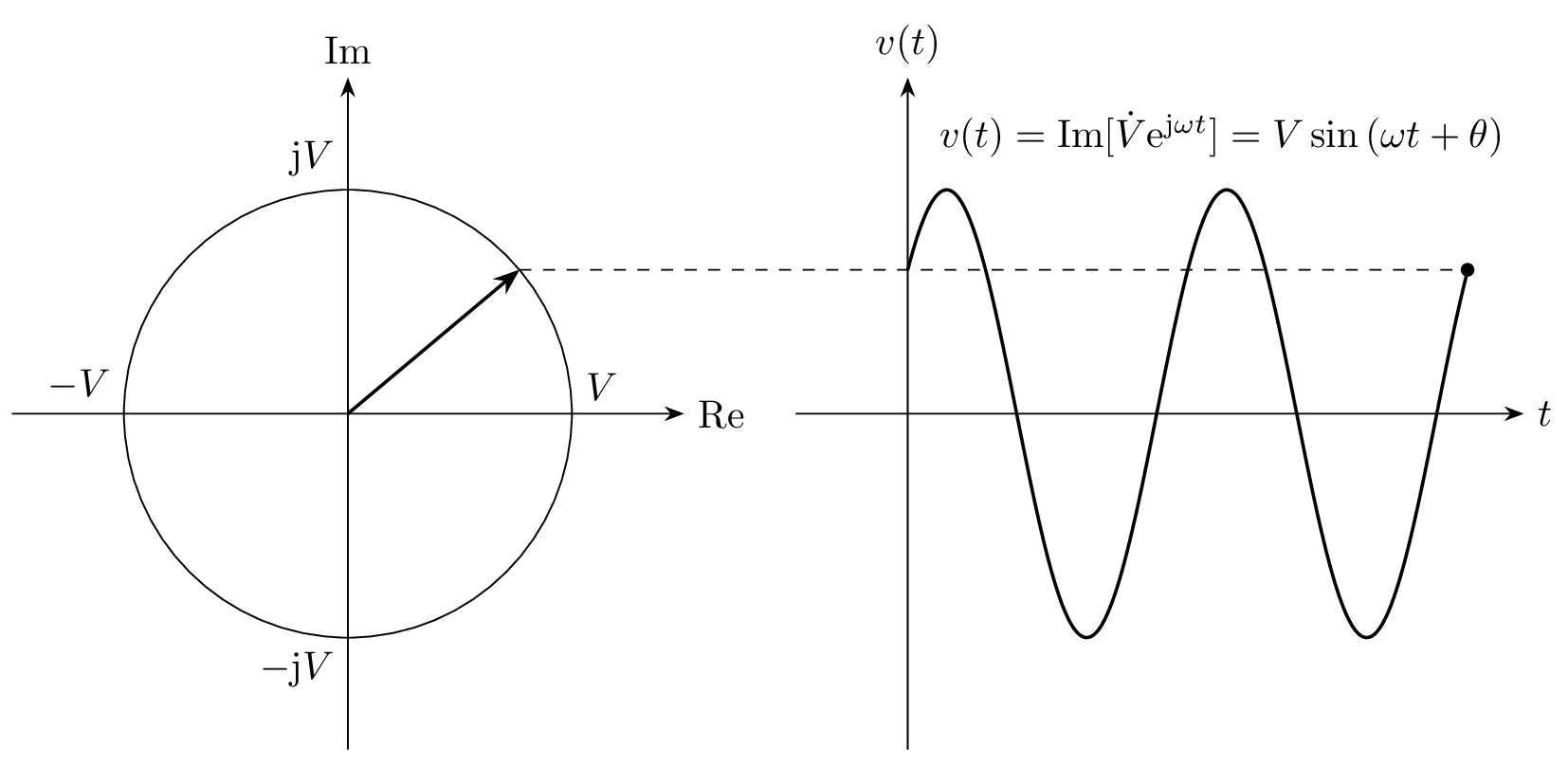
フェーザと交流信号の対応を表した図
フェーザ
フェーザ表示とフェーザ図
交流電圧のフェーザ表示を導入します。振幅 V、角周波数 \omega の交流電圧 v(t) を次式で与えます。
v(t) = V \sin (\omega t + \theta)
ここで、\theta は初期位相です。オイラーの公式より、
\mathrm{e}^{\mathrm{j}(\omega t + \theta)} = \cos (\omega t + \theta) + \mathrm{j} \sin (\omega t + \theta)
が成立するので、交流電圧 v(t) は次式で表すことができます。
v(t) = \text{Im} \left[ V \mathrm{e}^{\mathrm{j}(\omega t + \theta)} \right]
ただし、\text{Im}[\cdot] は複素数の虚部を取る操作です。ここで、大きさ V、位相 \theta の複素数 \dot{V}を定義します。
\dot{V} = V\mathrm{e}^{\mathrm{j}\theta} = V\angle \theta
これを用いると、電圧の瞬時値 v(t) は次式で表すことができます。
v(t) = \text{Im} \left[ \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right]
この複素数 \dot{V} を交流信号 v(t) のフェーザ (phasor) または複素振幅といいます。
フェーザ \dot{V} は複素数なので、複素平面上でベクトルとして表現することができ、これをフェーザ図といいます。
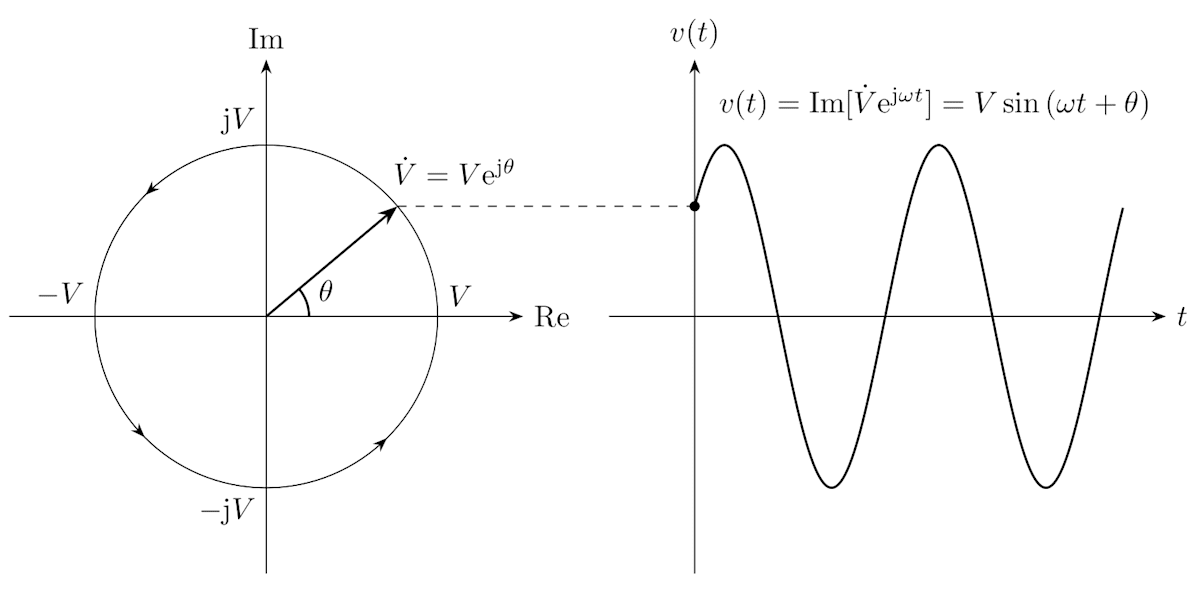
左:フェーザ図(横軸:実部、縦軸:虚部)、右:交流信号との対応
フェーザと瞬時値 v(t) の時間変化を下図に示します。フェーザ \dot{V} が角周波数 \omega で回転し、その虚部を取ったものが瞬時値として変換されているのが分かります。
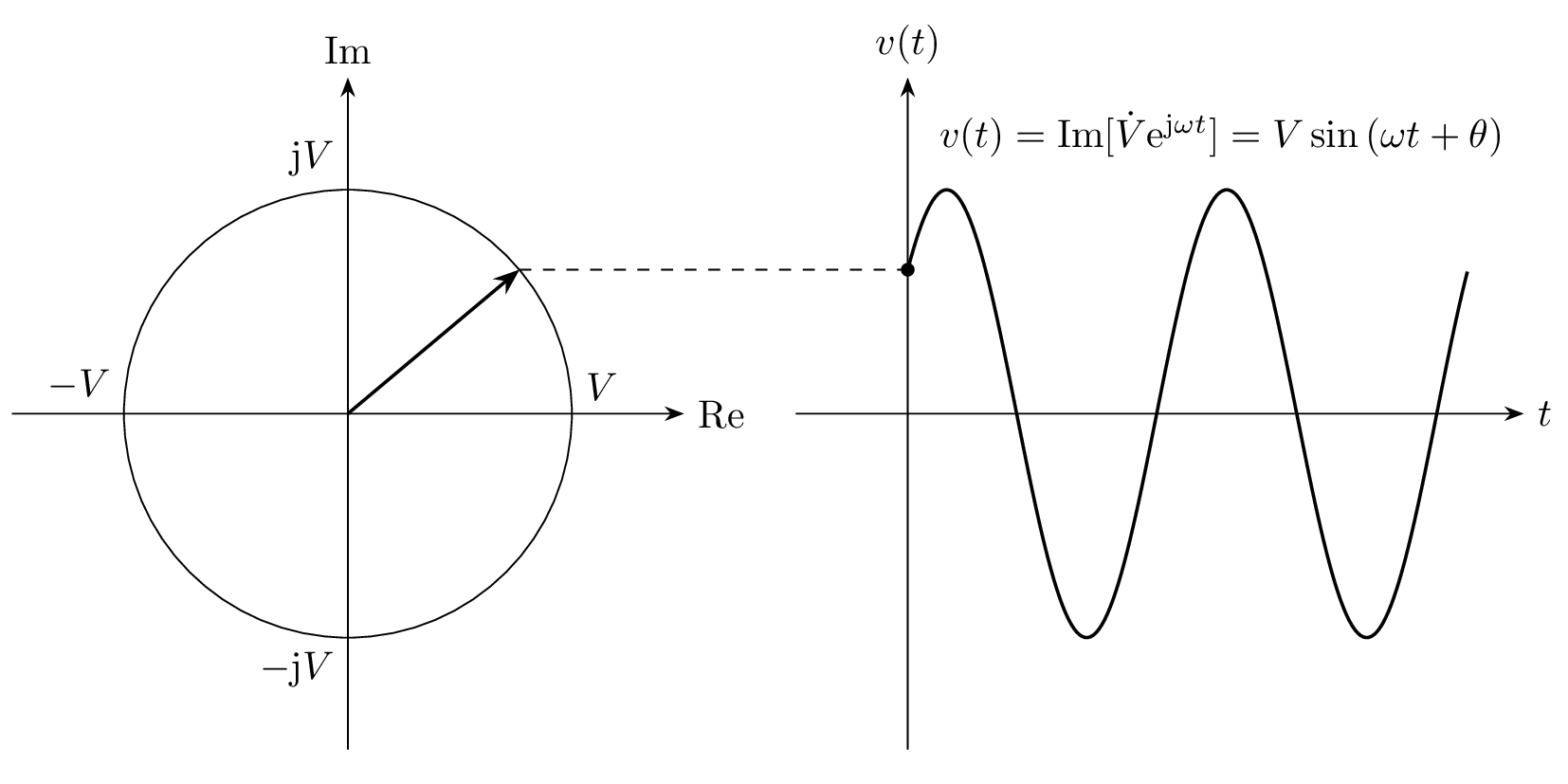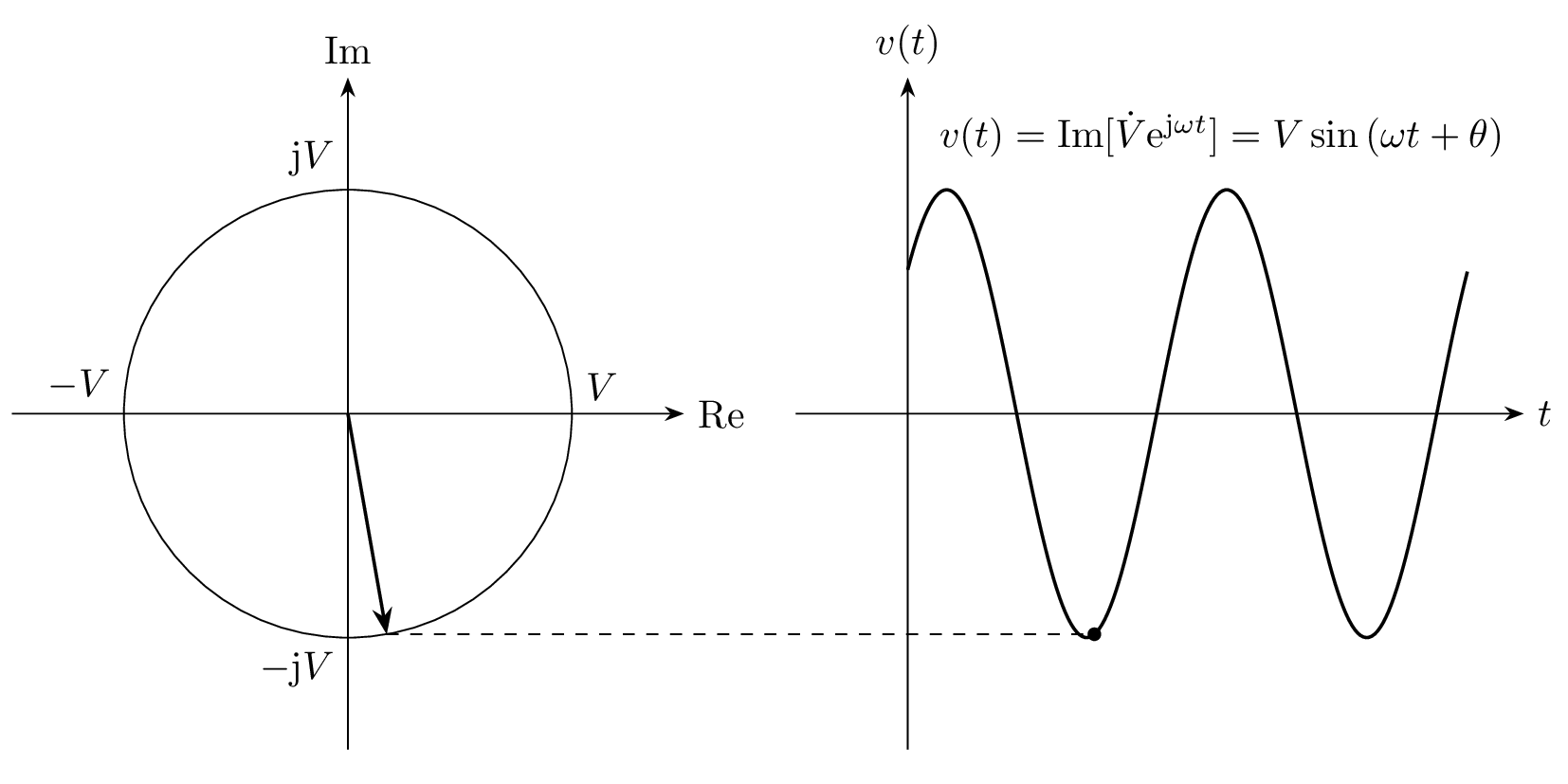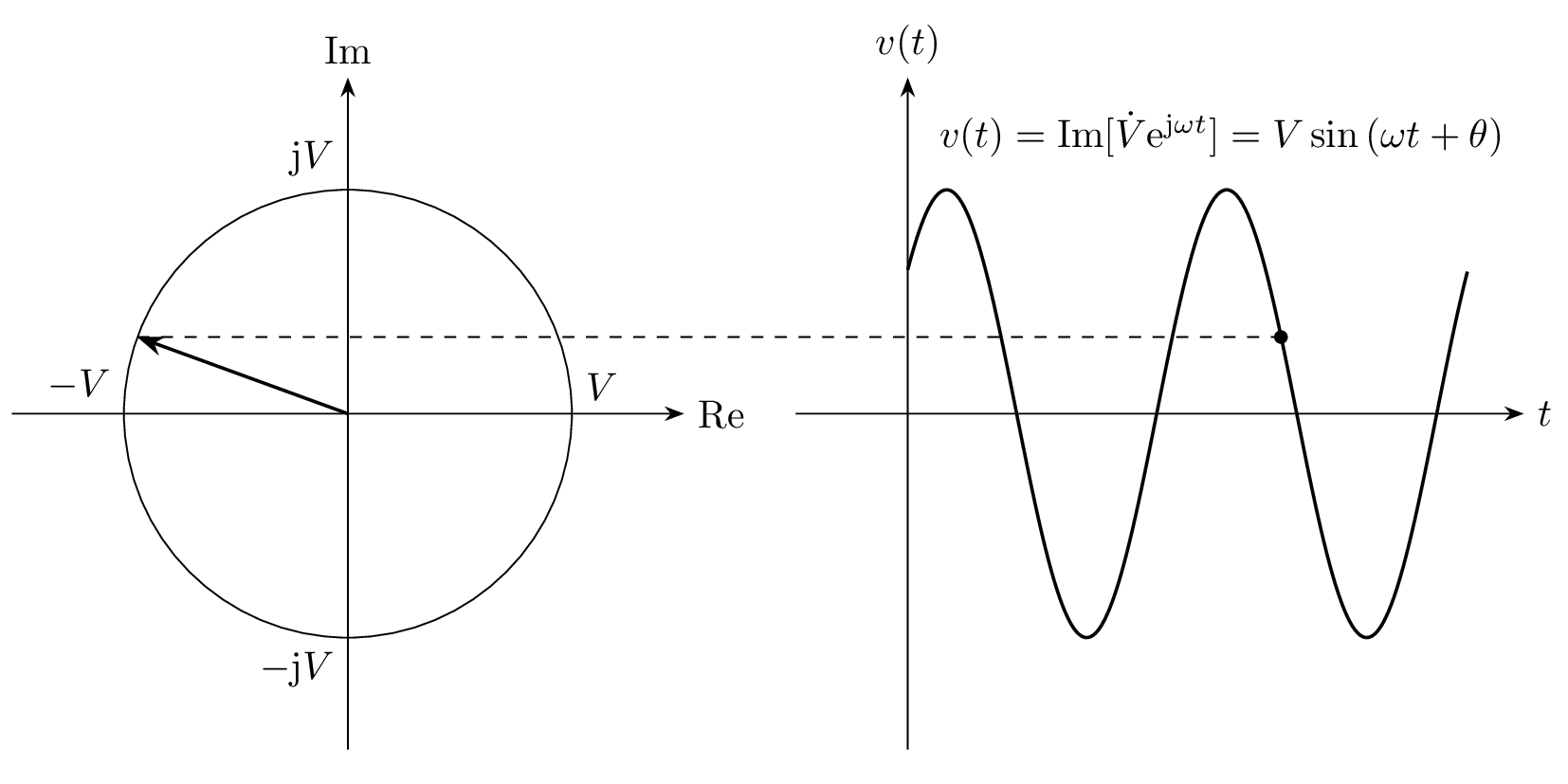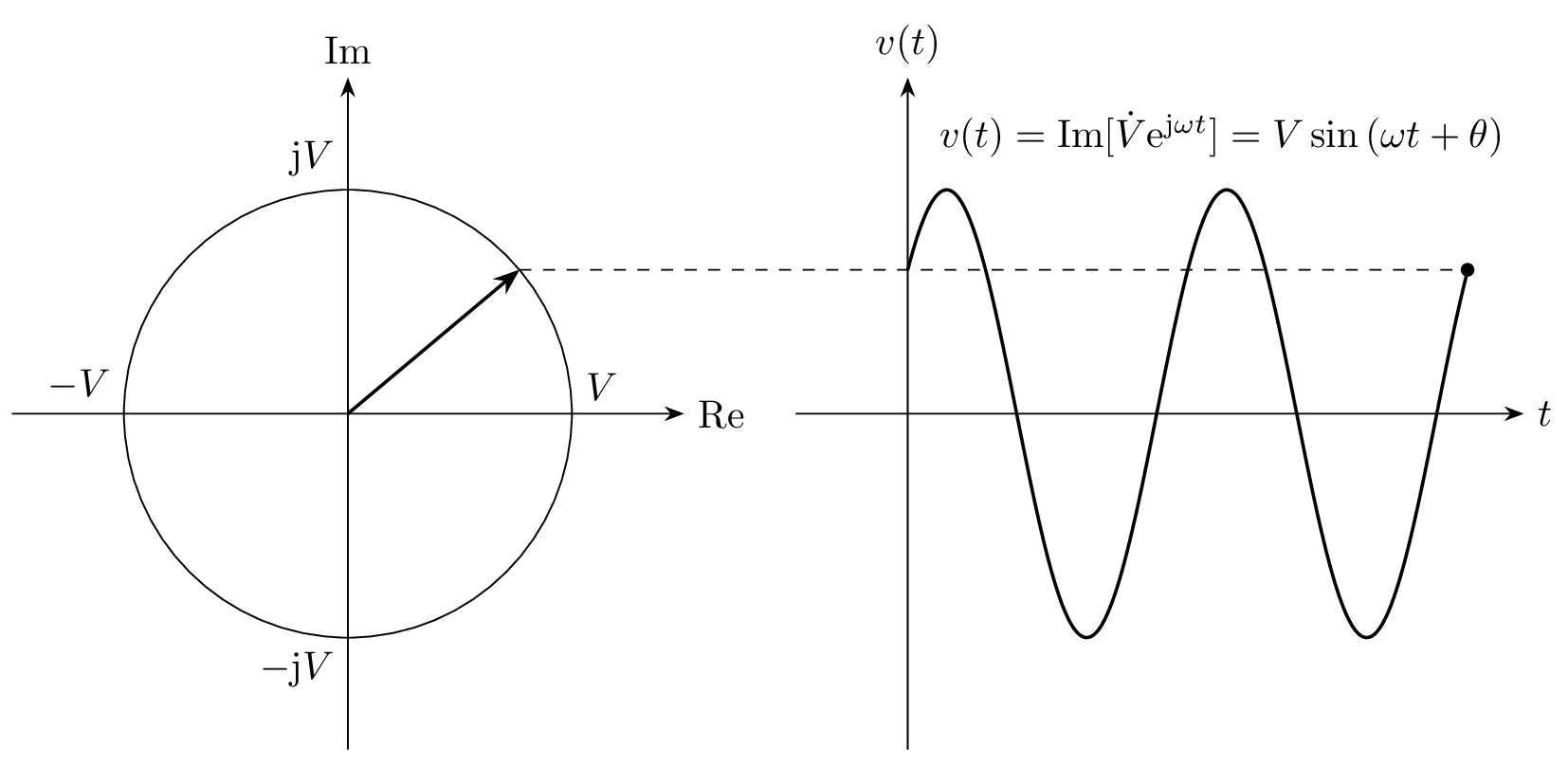
フェーザ \dot{V}と瞬時値 v(t) の時間変化を表した図
フェーザから瞬時値への4つの変換パターン
フェーザ \dot{V}=V\mathrm{e}^{\mathrm{j}\theta} から瞬時値 v(t) への変換方法には、以下の2点に自由度があります。
- 実部をとる or 虚部をとる
- フェーザの振幅 V を交流信号 v(t) の最大値とする or 実効値とする
各2通りの組み合わせを考慮すると、合計で4通りの変換方法が存在し、それぞれ以下の式で表されます。
| V |
実部をとる |
虚部をとる |
| 最大値 |
\mathrm{Re} \left[ \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right] = V \cos (\omega t + \theta) |
\mathrm{Im} \left[ \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right] = V \sin (\omega t + \theta) |
| 実効値 |
\mathrm{Re} \left[ \sqrt{2} \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right] = \sqrt{2} V \cos (\omega t + \theta) |
\mathrm{Im} \left[ \sqrt{2} \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right] = \sqrt{2} V \sin (\omega t + \theta) |
解析する上では、いずれかの定義に統一する必要があります。
電力の分野では実効値基準のフェーザを用いることが多いのに対して、電磁波解析の分野では最大値フェーザを用いることが多いようです[2]。
電圧則と電流則
電圧則・電流則はフェーザに対しても成立します。例えば、下図のループについて、フェーザに関する電圧則が成立します。
\dot{V}_1 + \dot{V}_2 + \dot{V}_3 = 0
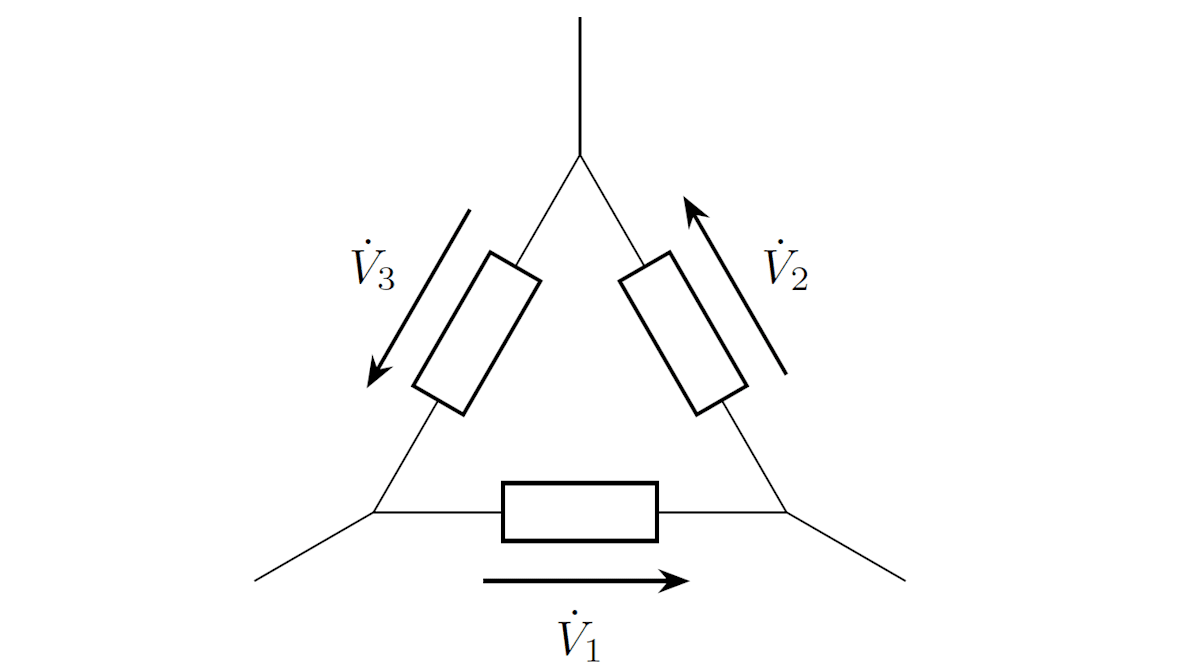
上式が成り立つことを確認してみましょう。各素子の電圧の瞬時値に関して
v_1(t) + v_2(t) + v_3(t) = 0
が成り立ちます。それぞれフェーザを用いて表現すると
\text{Re} \left[ \dot{V}_1 \mathrm{e}^{\mathrm{j}\omega t} \right] + \text{Re} \left[ \dot{V}_2 \mathrm{e}^{\mathrm{j}\omega t} \right] + \text{Re} \left[ \dot{V}_3 \mathrm{e}^{\mathrm{j}\omega t} \right] = 0
を得ます。一般の複素数 z_1, z_2 について
\text{Re}[z_1] + \text{Re}[z_2] = \text{Re}[z_1 + z_2]
が成り立つので、
\text{Re} \left[ \dot{V}_1 \mathrm{e}^{\mathrm{j}\omega t} + \dot{V}_2 \mathrm{e}^{\mathrm{j}\omega t} + \dot{V}_3 \mathrm{e}^{\mathrm{j}\omega t} \right] = 0
\therefore\quad \dot{V}_1 + \dot{V}_2 + \dot{V}_3 = 0
を得ます。よって、電圧則がフェーザに関しても成立することが示されました。
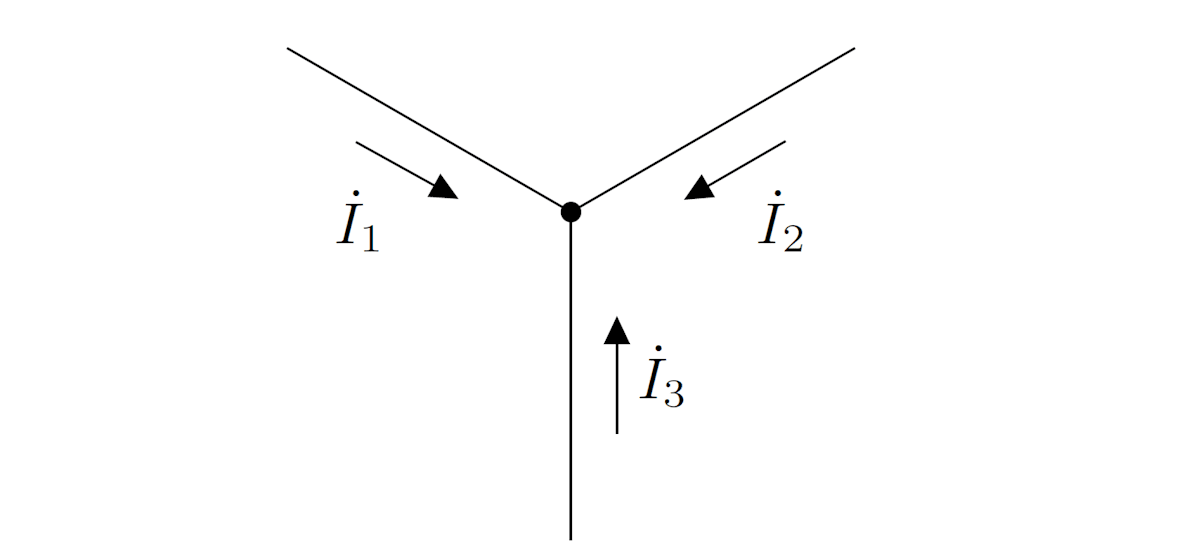
同様にして、任意の節点に流出入する電流のフェーザの和が 0 になることを示すことができます。
\dot{I}_1 + \dot{I}_2 + \dot{I}_3 = 0
回路素子とフェーザ表示
抵抗 R、インダクタンス L、コンデンサ Cそれぞれの電圧と電流の関係をフェーザで表現してみましょう。特に、インダクタンス L、コンデンサ C は時間領域における微分・積分操作が、\mathrm{j}\omega, 1/\mathrm{j}\omega の積として表現されるという重要な性質があります。
抵抗にかかる電圧と電流の関係
抵抗 R にかかる電圧、電流を v(t), i(t) とすると、オームの法則より次式が成立します。
電圧、電流のフェーザを \dot{V}, \dot{I} とすると以下の関係式を得ます。
\text{Re} \left[ \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right] = R \cdot \text{Re} \left[ \dot{I} \mathrm{e}^{\mathrm{j}\omega t} \right]
= \text{Re} \left[ R \dot{I} \mathrm{e}^{\mathrm{j}\omega t} \right]
この式は任意の t について成立する必要があるため、フェーザも時間領域における表現と同様に、オームの法則が成り立ちます。
R は実数なので、抵抗にかかる電圧と電流は同位相になり、\dot{V}, \dot{I} はフェーザ図上で平行になります。
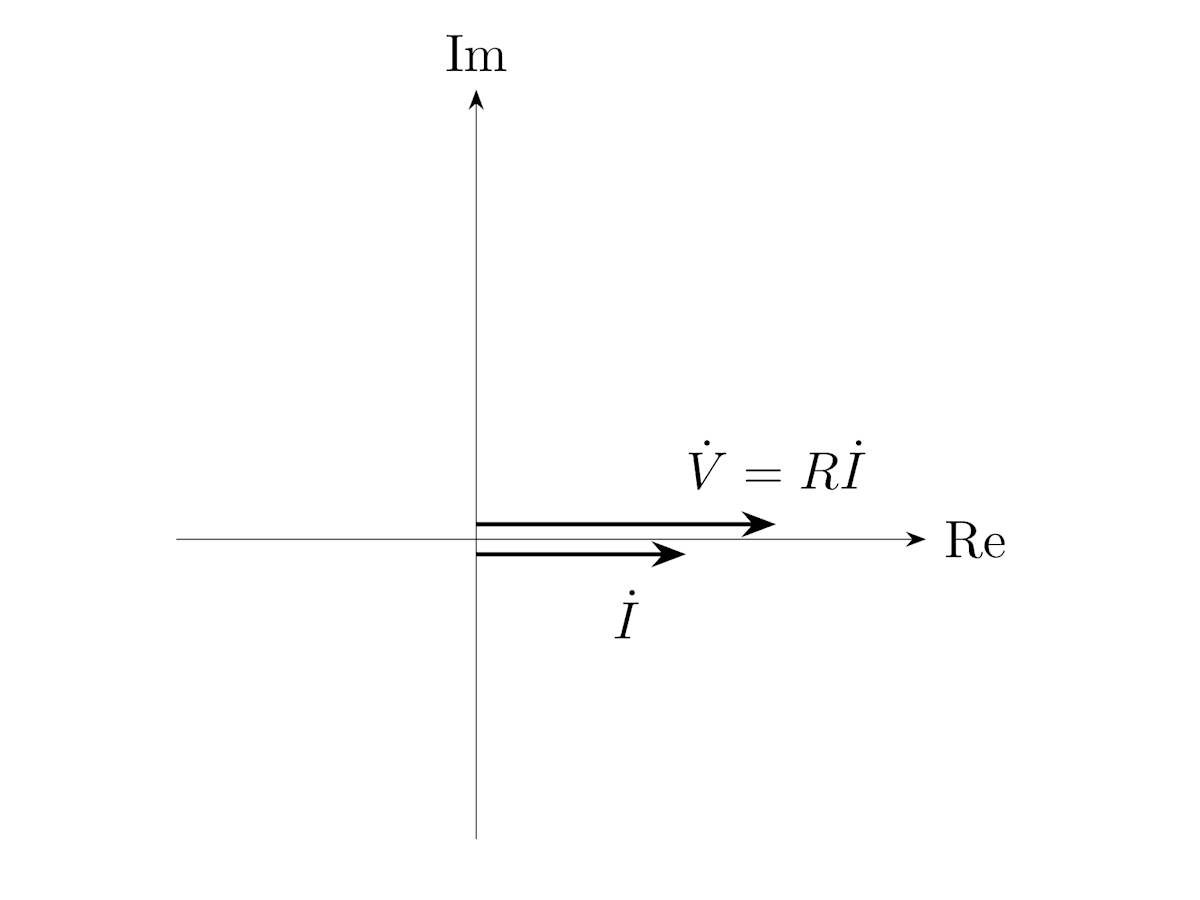
インダクタにかかる電圧と電流の関係
インダクタ L にかかる電圧、電流を v(t), i(t) とすると、
v(t) = L \frac{\mathrm{d}i}{\mathrm{d}t}
と表されます。電圧、電流のフェーザを \dot{V}, \dot{I} とすると以下の関係式を得ます。
\text{Re} \left[ \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right] = L \frac{\mathrm{d}}{\mathrm{d}t} \text{Re} \left[ \dot{I} \mathrm{e}^{\mathrm{j}\omega t} \right]
= \text{Re} \left[ L \frac{\mathrm{d}}{\mathrm{d}t} \dot{I} \mathrm{e}^{\mathrm{j}\omega t} \right]
= \text{Re} \left[ \mathrm{j}\omega L \dot{I} \mathrm{e}^{\mathrm{j}\omega t} \right]
この式は任意の t について成立する必要があるため、次式を得ます。
\dot{V} = \mathrm{j}\omega L \dot{I}
形式的にインダクタを \mathrm{j}\omega L の抵抗成分を持つ素子として解釈すると、オームの法則が成立することが分かります。この抵抗成分をインダクタのインピーダンス (impedance) と呼びます。
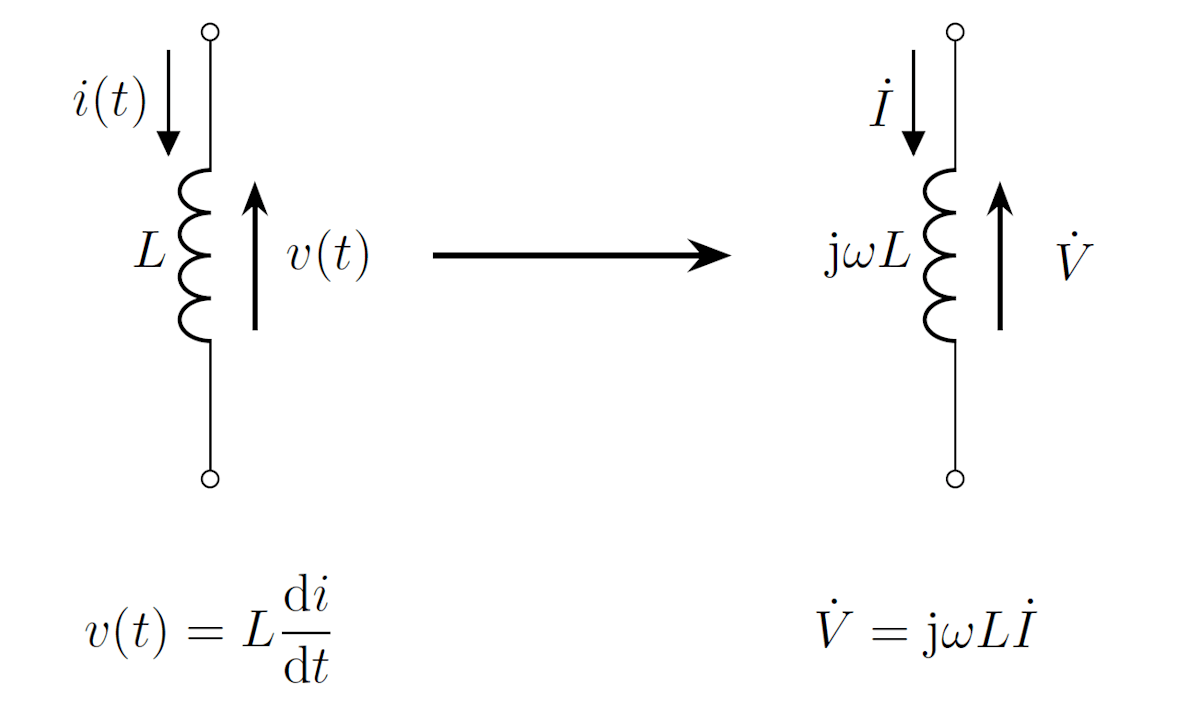
インダクタ L のインピーダンスは \mathrm{j}\omega L
電圧と電流の位相について考えると、電流 \dot{I} に \mathrm{j} = \mathrm{e}^{\mathrm{j}\frac{\pi}{2}} がかけられているので、電圧 \dot{V} に対して電流 \dot{I} は 90^\circ 遅れます。フェーザ図で描くと、\dot{V}, \dot{I}は直交します。
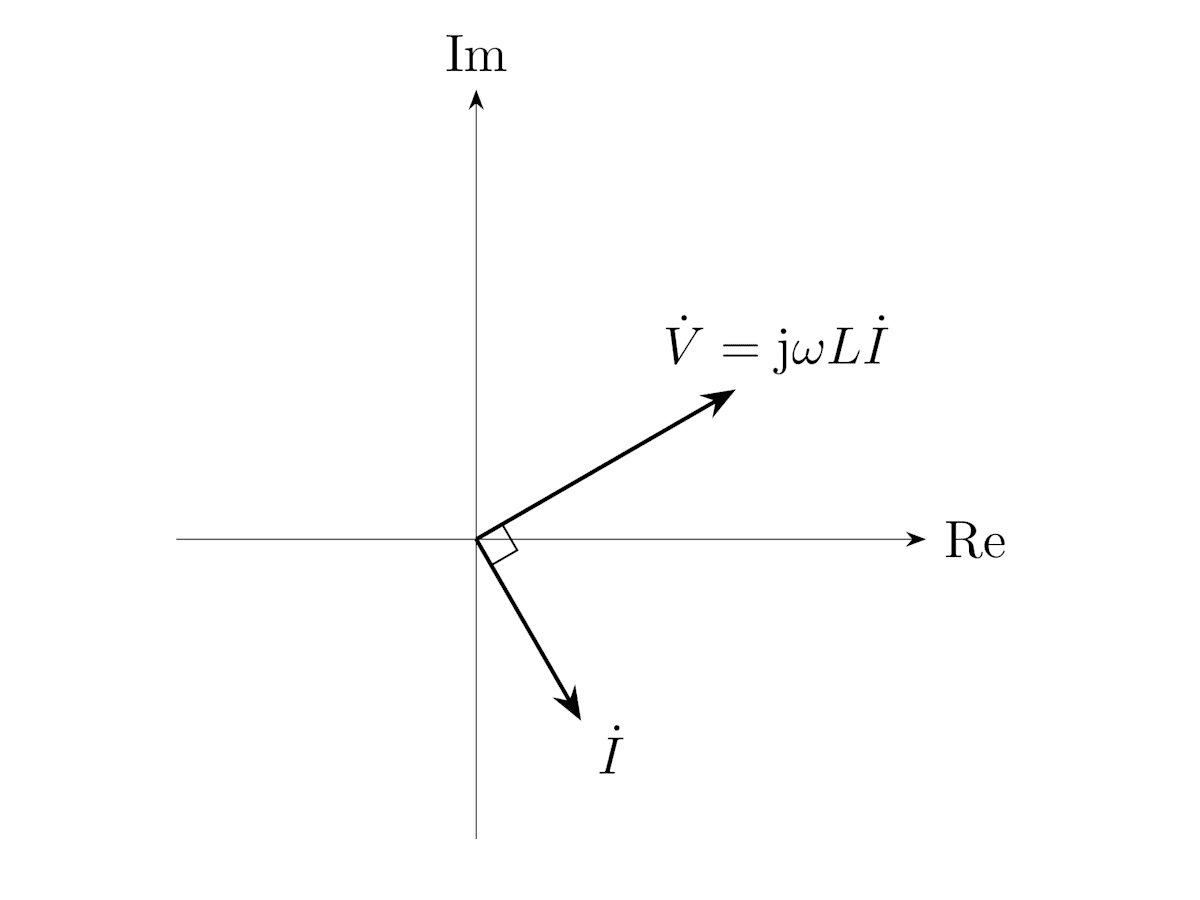
フェーザと瞬時値 v(t), i(t) の時間変化を下図に示します。交流電圧 v(t) に対して、交流電流 i(t) が 90^\circだけ遅れていることが分かります。
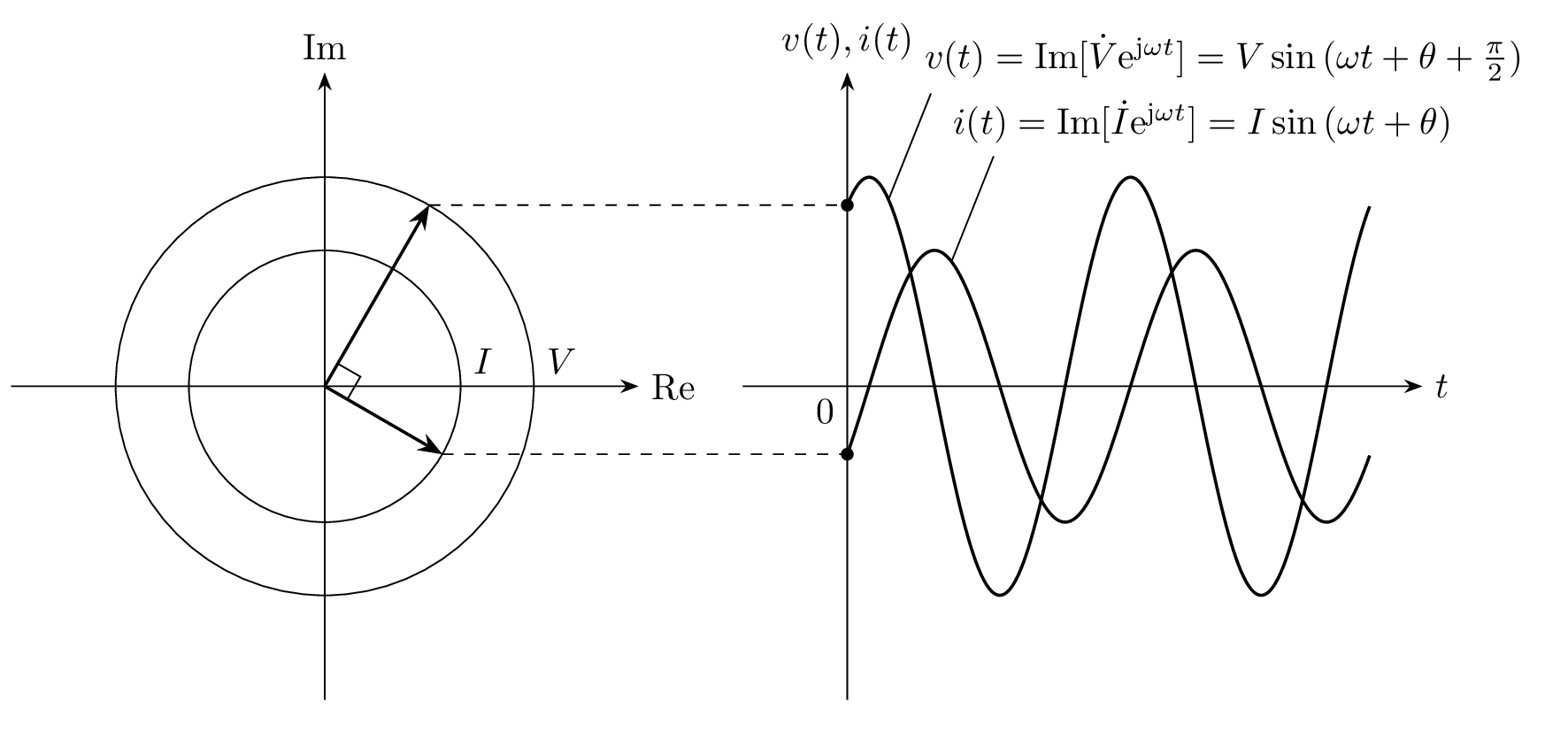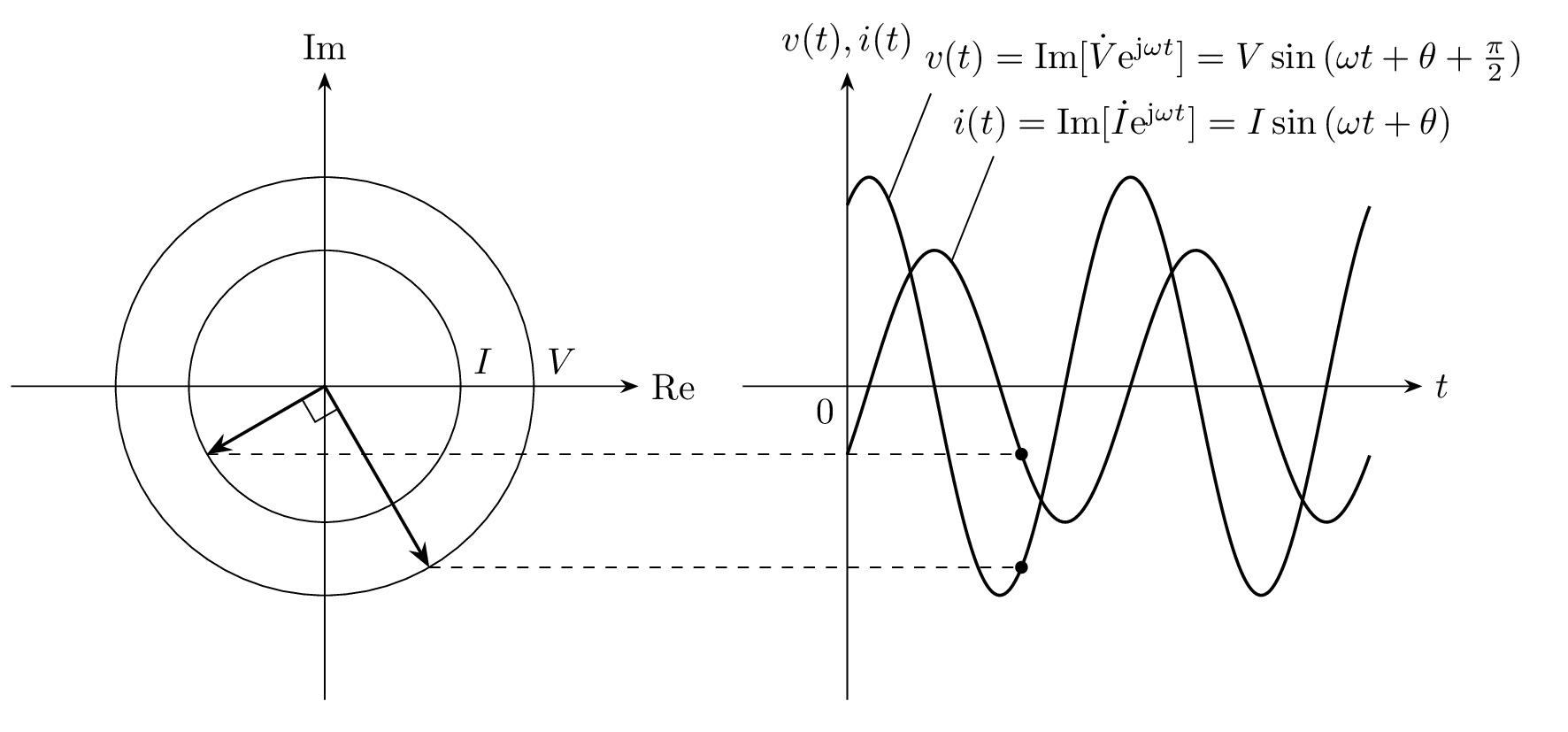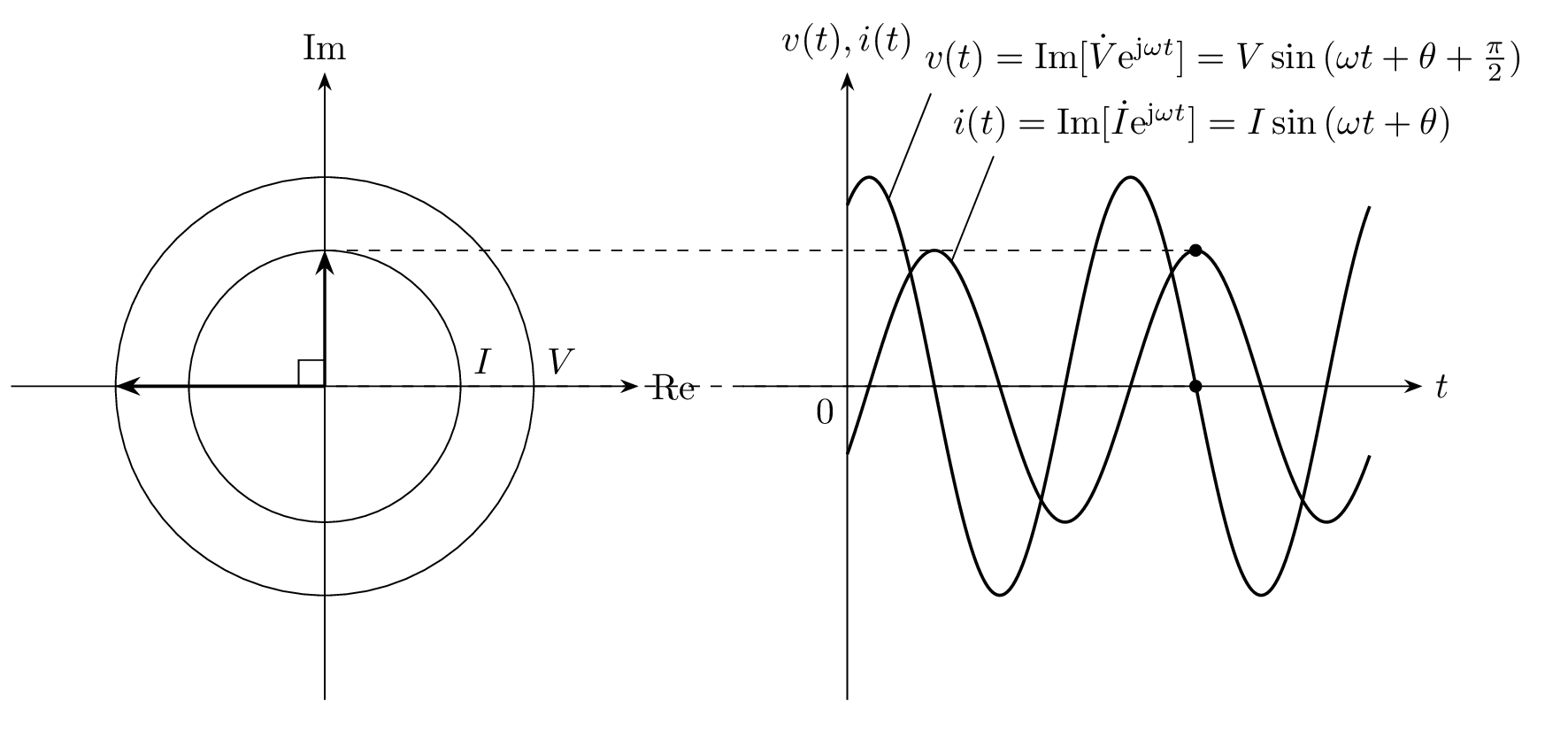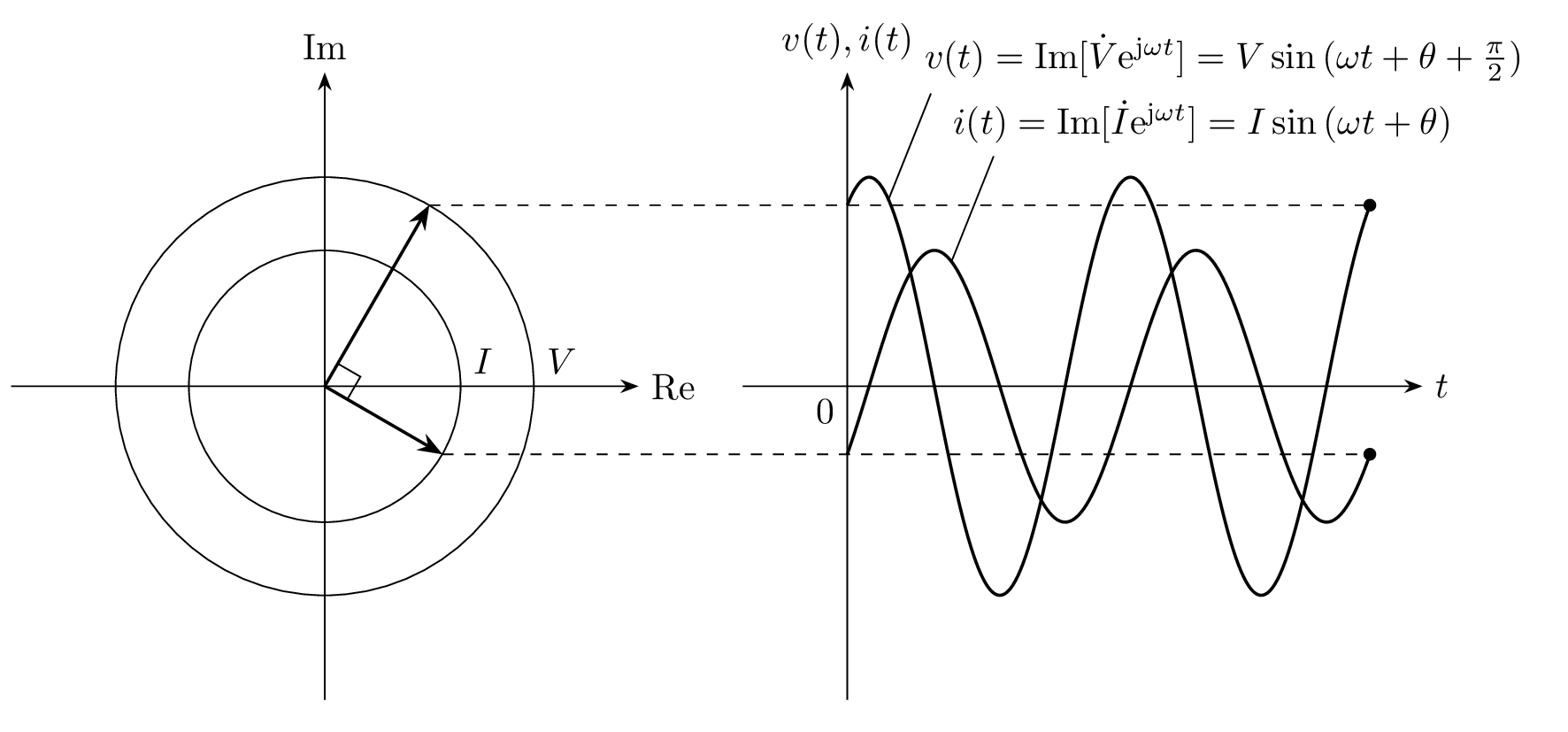
フェーザ \dot{V}, \dot{I} と交流信号 v(t), i(t) の対応を表した図
コンデンサにかかる電圧と電流の関係
コンデンサ C にかかる電圧、電流を v(t), i(t) とすると、
v(t) = \frac{1}{C} \int i(t) \mathrm{d}t
と表されます。電圧、電流のフェーザを \dot{V}, \dot{I} とすると以下の関係式を得ます。
\text{Re} \left[ \dot{V} \mathrm{e}^{\mathrm{j}\omega t} \right] = \frac{1}{C} \int \text{Re} \left[ \dot{I} \mathrm{e}^{\mathrm{j}\omega t} \right] \mathrm{d}t
= \text{Re} \left[ \frac{\dot{I}}{\mathrm{j}\omega C} \mathrm{e}^{\mathrm{j}\omega t} \right]
この式は任意の t について成立する必要があるため、次式を得ます。
\dot{V} = \frac{\dot{I}}{\mathrm{j}\omega C}
形式的にコンデンサを 1/\mathrm{j}\omega C の抵抗成分を持つ素子として解釈すると、オームの法則が成立することが分かります。
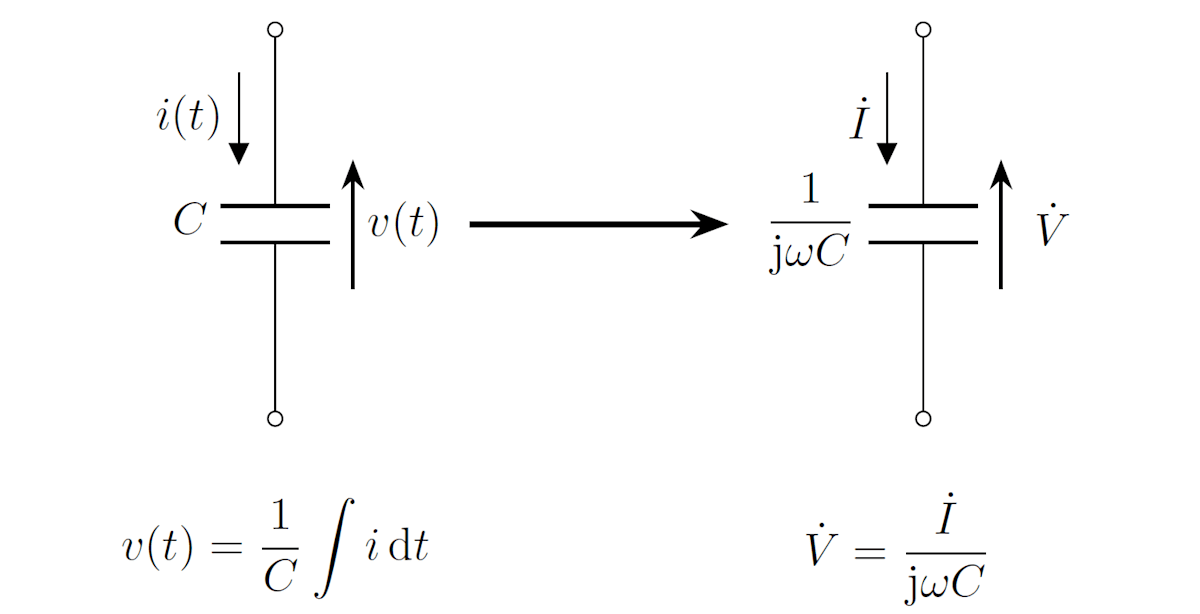
コンデンサ C のインピーダンスは 1/\mathrm{j}\omega C
電圧と電流の位相について考えると、電流 \dot{I} に 1/\mathrm{j} = \mathrm{e}^{-\mathrm{j}\frac{\pi}{2}} がかけられているので、電圧 \dot{V} に対して電流 \dot{I} は 90^\circ 進みます。
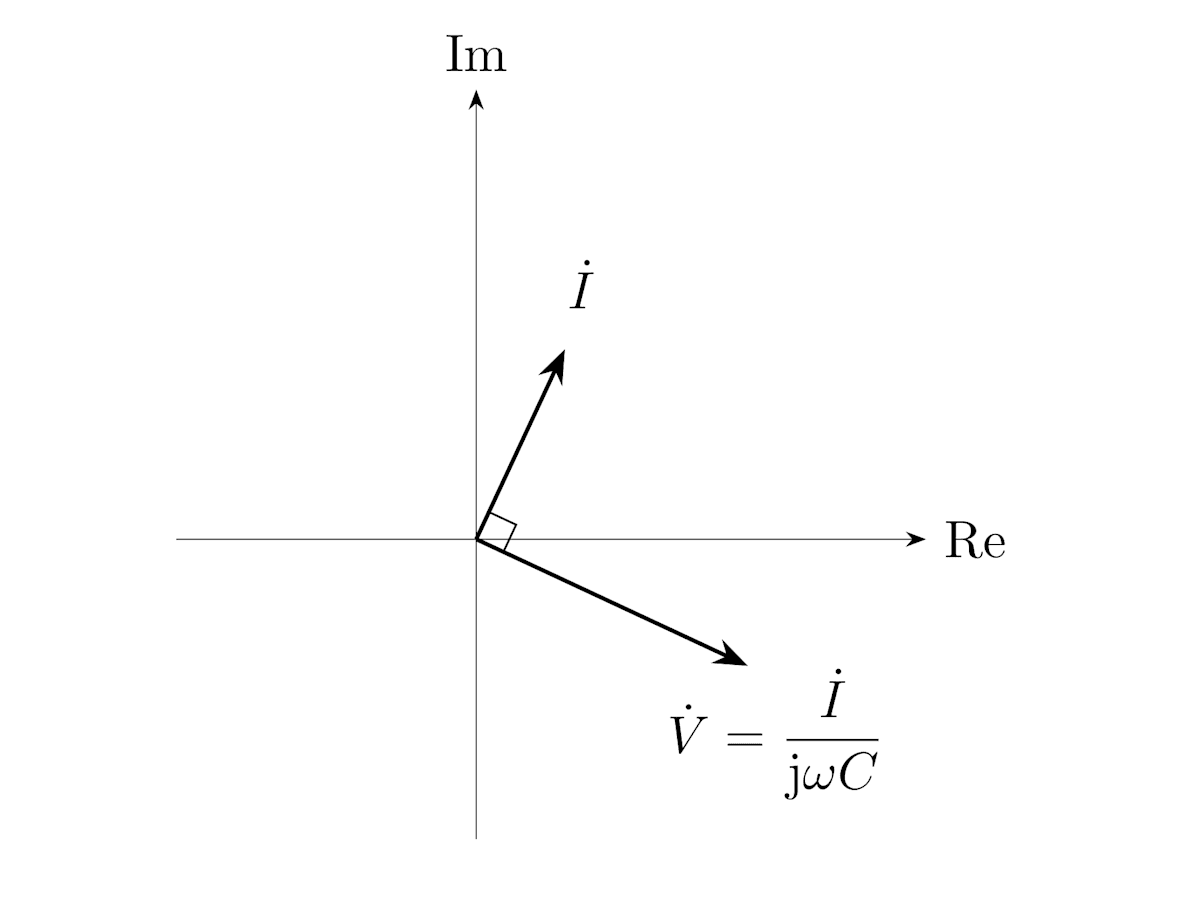
フェーザと瞬時値 v(t), i(t) の時間変化を下図に示します。交流電圧 v(t) に対して、交流電流 i(t) が 90^\circだけ進んでいることが分かります。
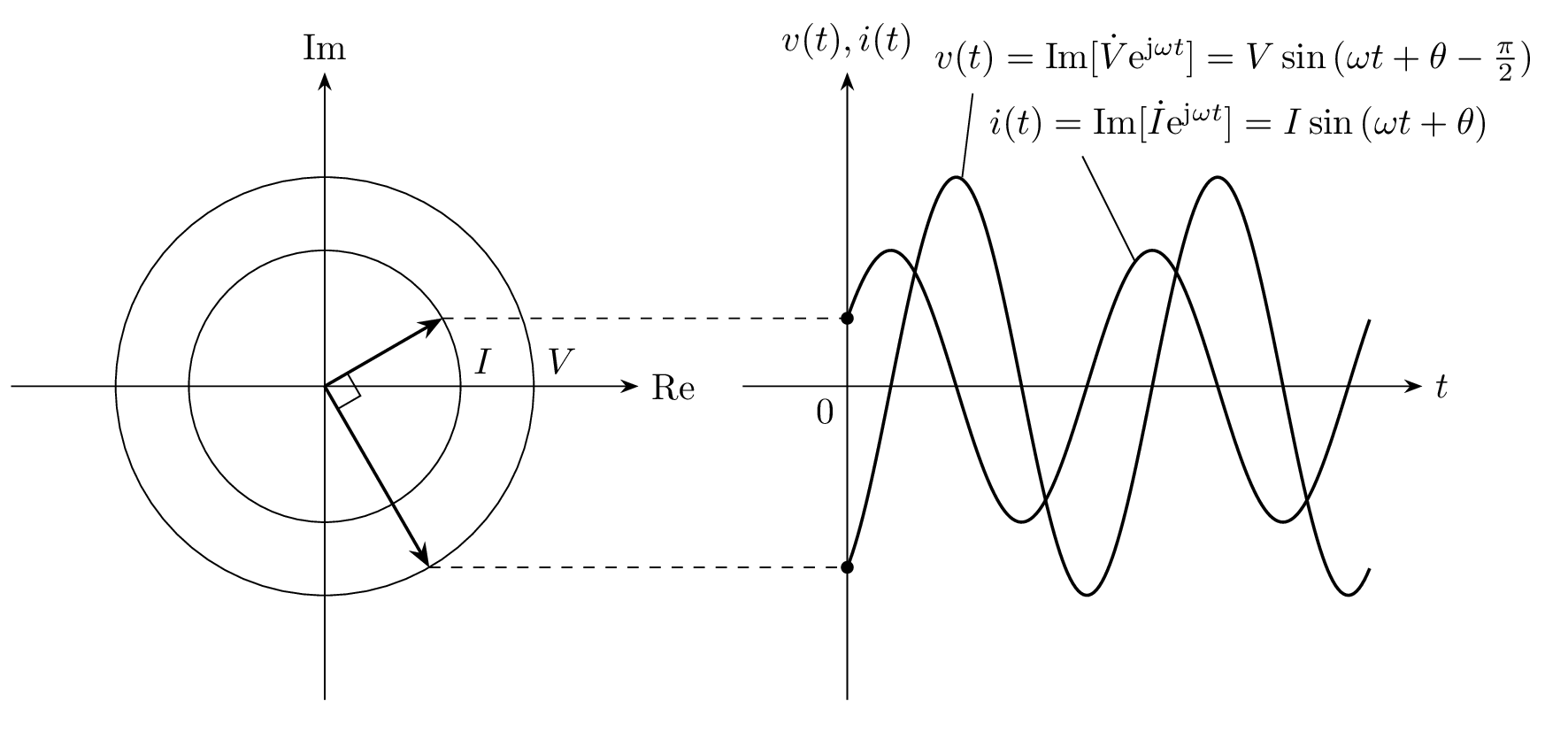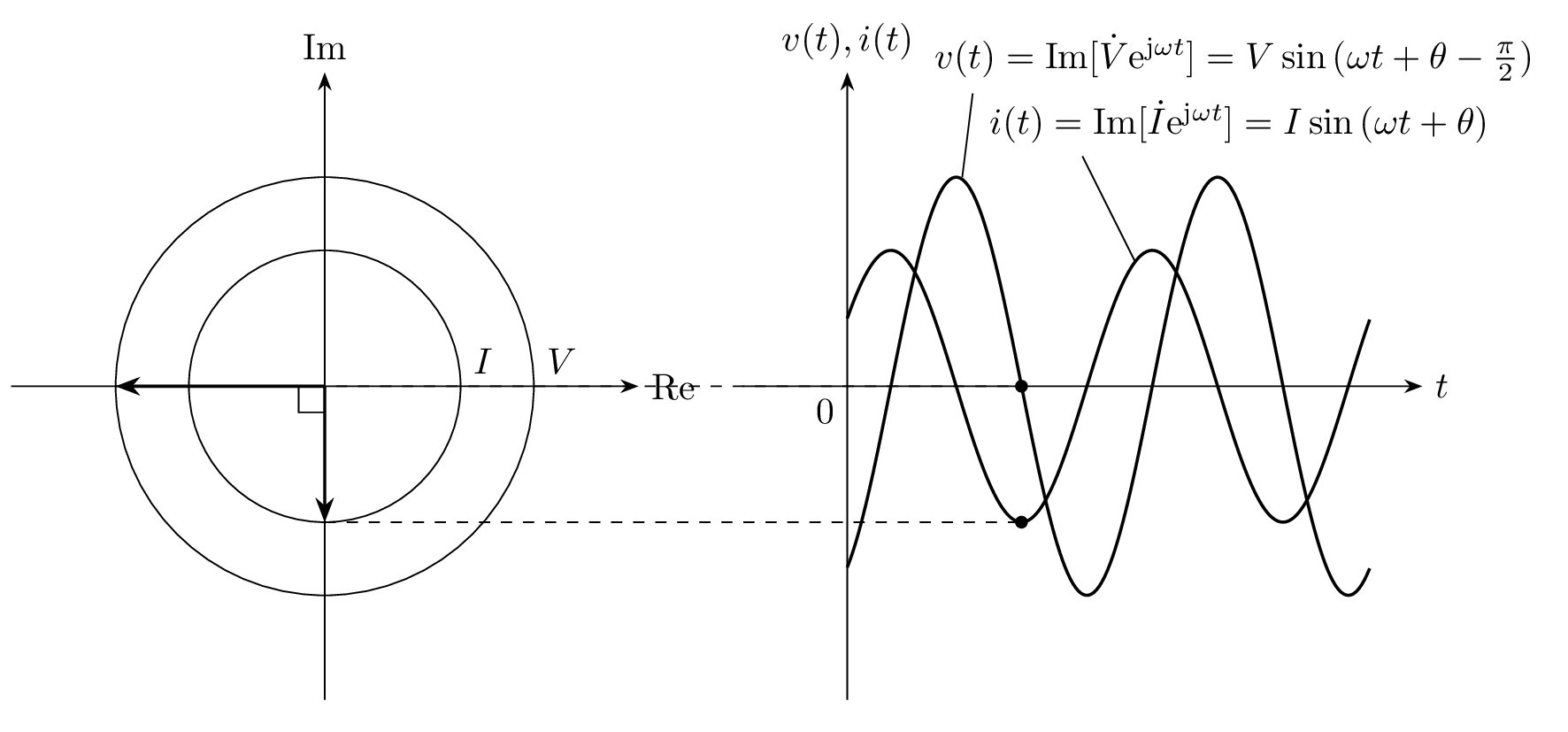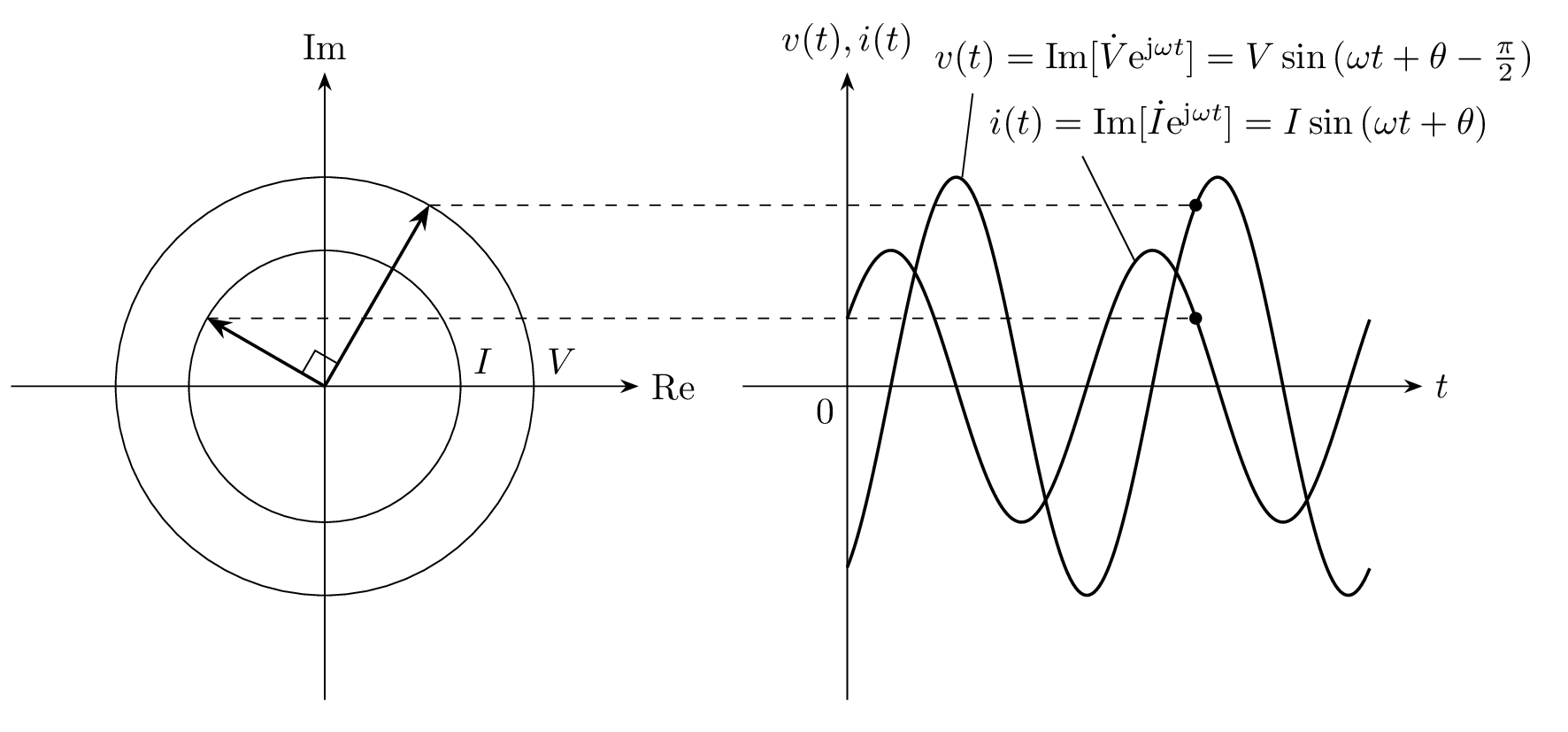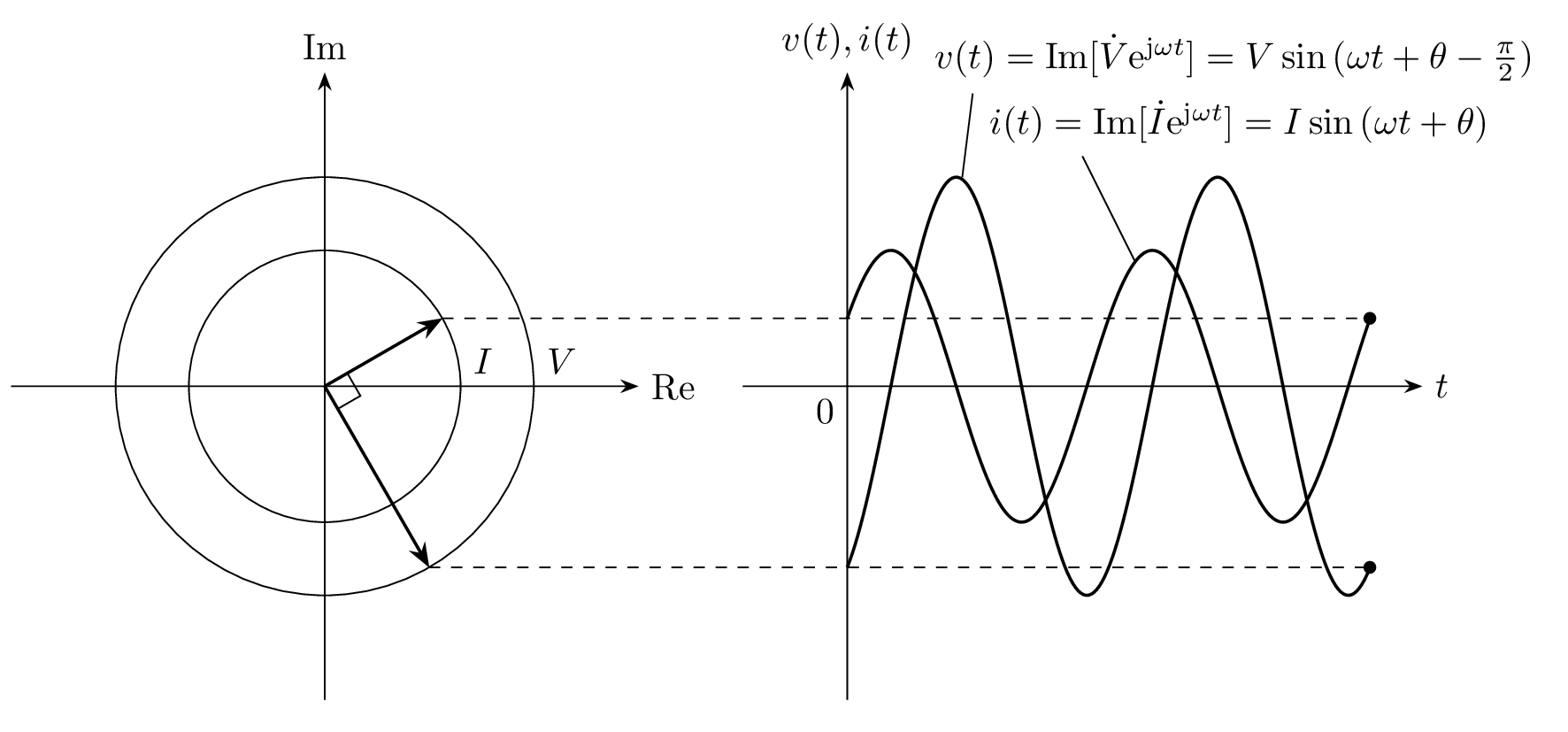
フェーザ \dot{V}, \dot{I} と交流信号 v(t), i(t) の対応を表した図
インピーダンスとアドミタンス
2端子間の電圧フェーザが \dot{V}、電流フェーザが \dot{I} のとき、その比 \dot{Z} をインピーダンス (impedance) と呼び、単位は通常の抵抗と同じくオーム \Omega です。
\dot{Z} = \frac{\dot{V}}{\dot{I}}

2端子間の電圧フェーザ \dot{V} と電流フェーザ \dot{I} の比をインピーダンス \dot{Z} という
具体例として、直列接続したRLC回路を考えます。
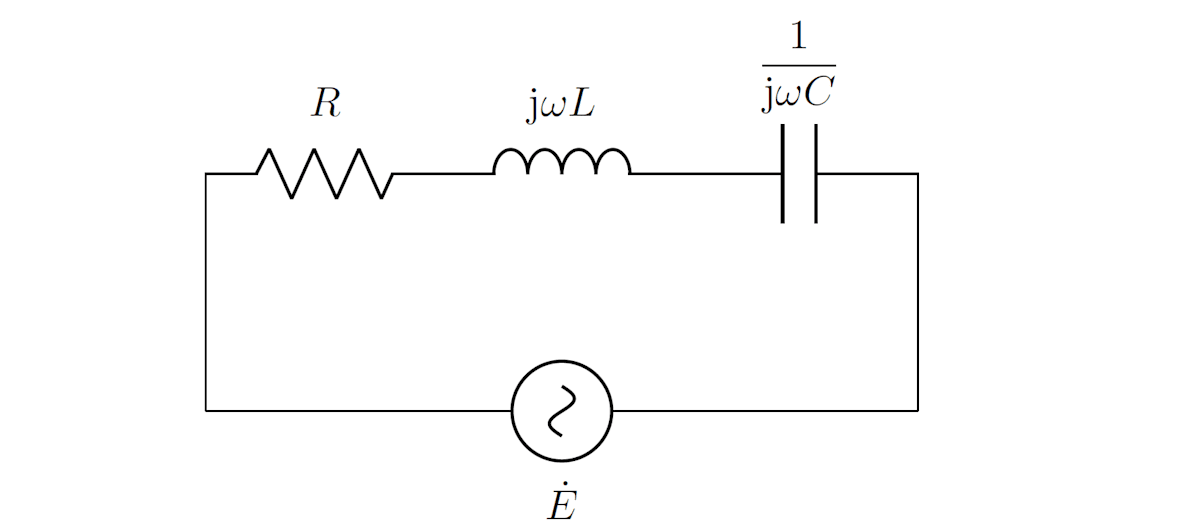
抵抗・インダクタ・コンデンサそれぞれの電圧のフェーザを \dot{V}_R, \dot{V}_L, \dot{V}_C、電圧源のフェーザを \dot{E} とすると、電圧則より次式が成立します。
\dot{V}_R + \dot{V}_L + \dot{V}_C = \dot{E}
それぞれのインピーダンスを考えると、回路に流れる電流のフェーザを \dot{I} として
\left( R + \mathrm{j}\omega L + \frac{1}{\mathrm{j}\omega C} \right) \dot{I} = \dot{E}
を得ます。よって、直列接続したRLC回路のインピーダンス \dot{Z} は次式で表されます。
\dot{Z} = R + \mathrm{j}\omega L + \frac{1}{\mathrm{j}\omega C}
インピーダンスの逆数はアドミタンス (admittance) と呼ばれ、単位はジーメンス \mathrm{S} です。アドミタンスを \dot{Y}とおくと次式で与えられます。
\dot{Y} = \frac{1}{\dot{Z}} = \frac{\dot{I}}{\dot{V}}
なお、イミタンス (immitance) はインピーダンスとアドミタンスを総称したものです。インピーダンスとアドミタンスを同時に扱いたいときに使われ、次元は存在しません。
インピーダンス \dot{Z} = R + \mathrm{j}X の実部 R と虚部 X はそれぞれ抵抗分・リアクタンス分 (reactance) と呼ばれます。また、アドミタンス \dot{Y} = G + \mathrm{j}B の実部 G と虚部 B はそれぞれコンダクタンス分・サセプタンス分 (susceptance) と呼ばれます。
例題:RLC回路
下図の回路において、電源電圧 e(t) = E \sin \omega t を印加したとき、以下の問題に答えてください。ただし、E = 100\sqrt{2} \, \mathrm{V}, \, \omega = 10000 \, \mathrm{rad/s} とし、フェーザの振幅は最大値として扱ってください。
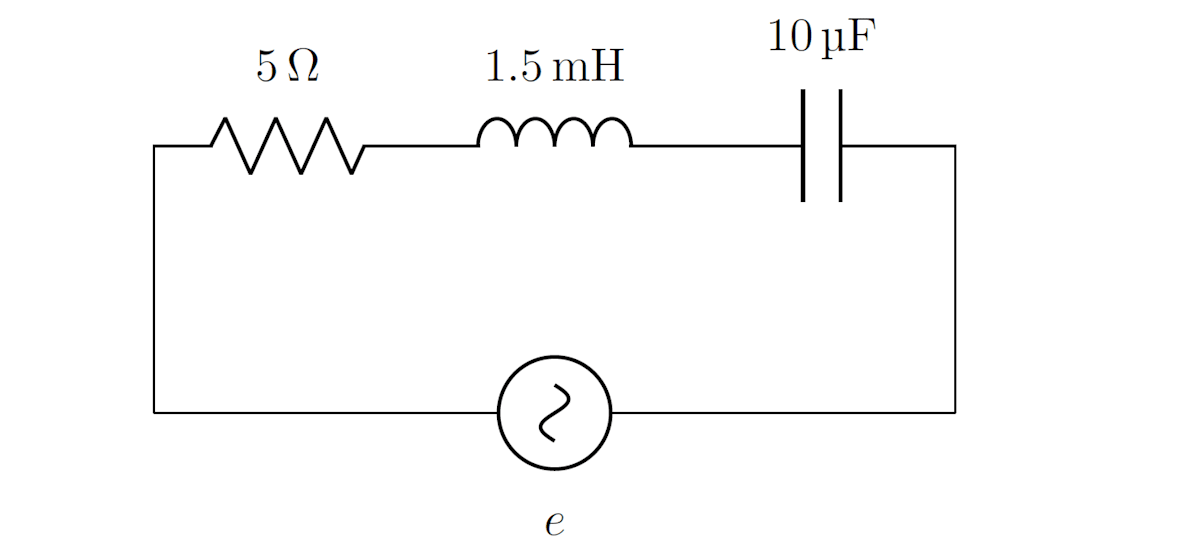
(1) 回路のインピーダンス \dot{Z} を求めてください。
答え
\begin{align*}
\dot{Z} &= R + \mathrm{j}\omega L + \frac{1}{\mathrm{j}\omega C} \\
&= 5 + \mathrm{j}5 \\
&= 5\sqrt{2} \mathrm{e}^{\mathrm{j}\frac{\pi}{4}} \left( = 5\sqrt{2}\angle \frac{\pi}{4}\right)
\end{align*}
(2) 回路に流れる電流のフェーザ \dot{I} および瞬時値 i(t) を求めてください。
答え
電源電圧のフェーザ \dot{E} は \dot{E} = 100\sqrt{2} と表せるので、電流のフェーザ \dot{I} は次式で表されます。
\dot{I} = \frac{\dot{E}}{\dot{Z}} = \frac{100\sqrt{2}}{5\sqrt{2} \mathrm{e}^{\mathrm{j}\frac{\pi}{4}}} = 20 \mathrm{e}^{-\mathrm{j}\frac{\pi}{4}} \left( = 20\angle -\frac{\pi}{4}\right)
瞬時値 i(t) は次式で与えられます。
i(t) = \text{Im} \left[ \dot{I} \mathrm{e}^{\mathrm{j}\omega t} \right] = \text{Im} \left[ 20 \mathrm{e}^{\mathrm{j}(\omega t - \frac{\pi}{4})} \right] = 20 \sin{\left( \omega t - \frac{\pi}{4} \right)}
与えられたRLC回路に流れる電流 i(t)は、電源電圧 e(t) に対して 45^\circ 遅れます。
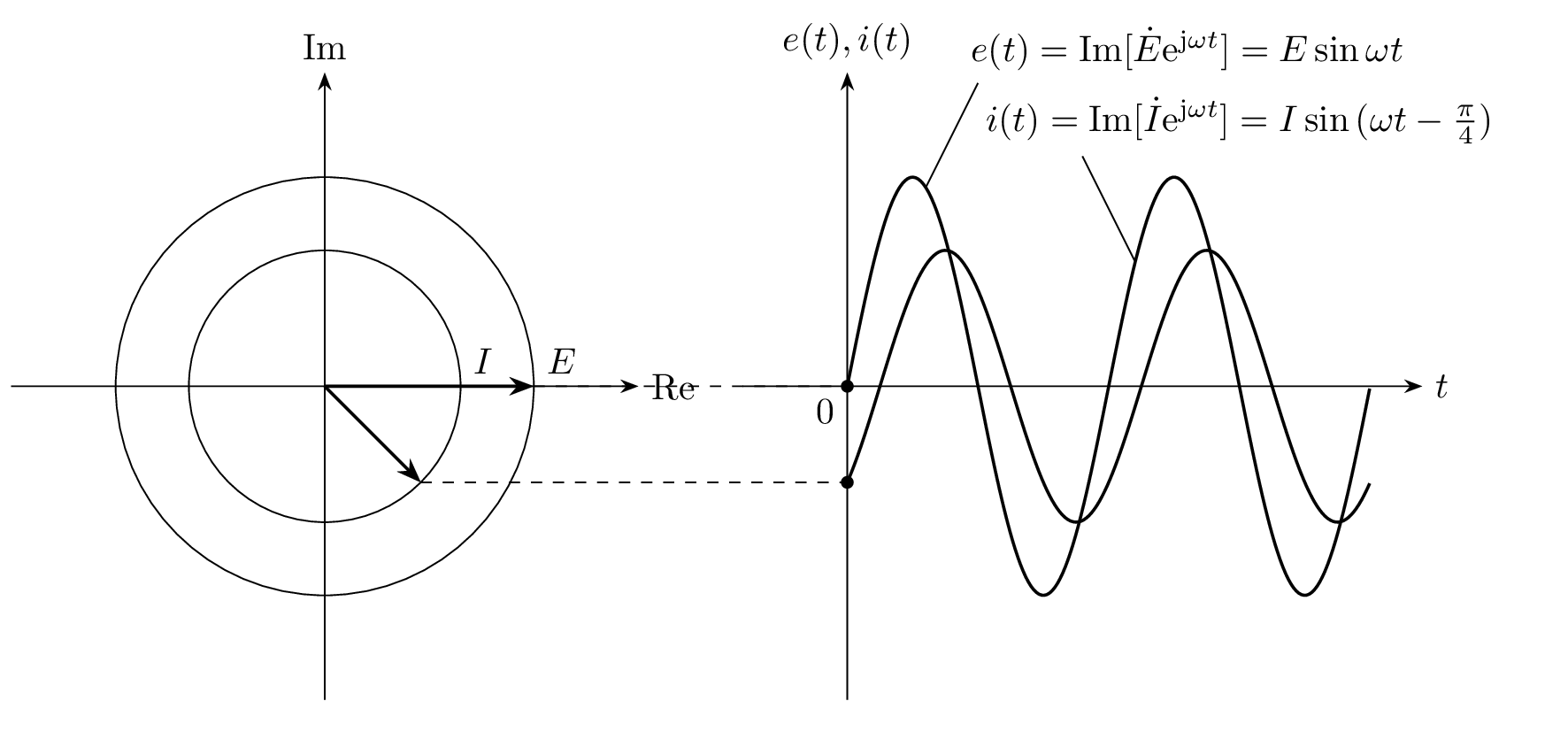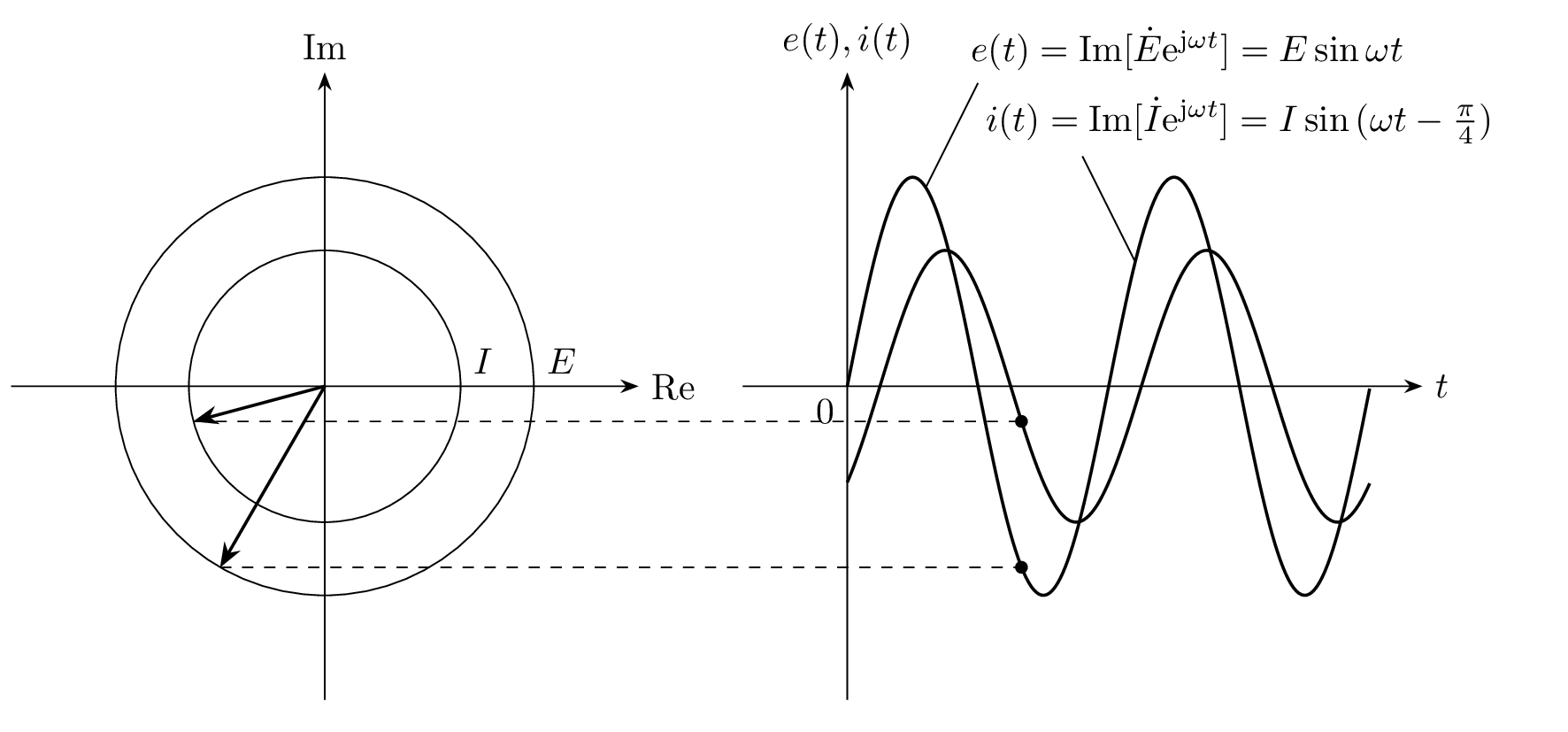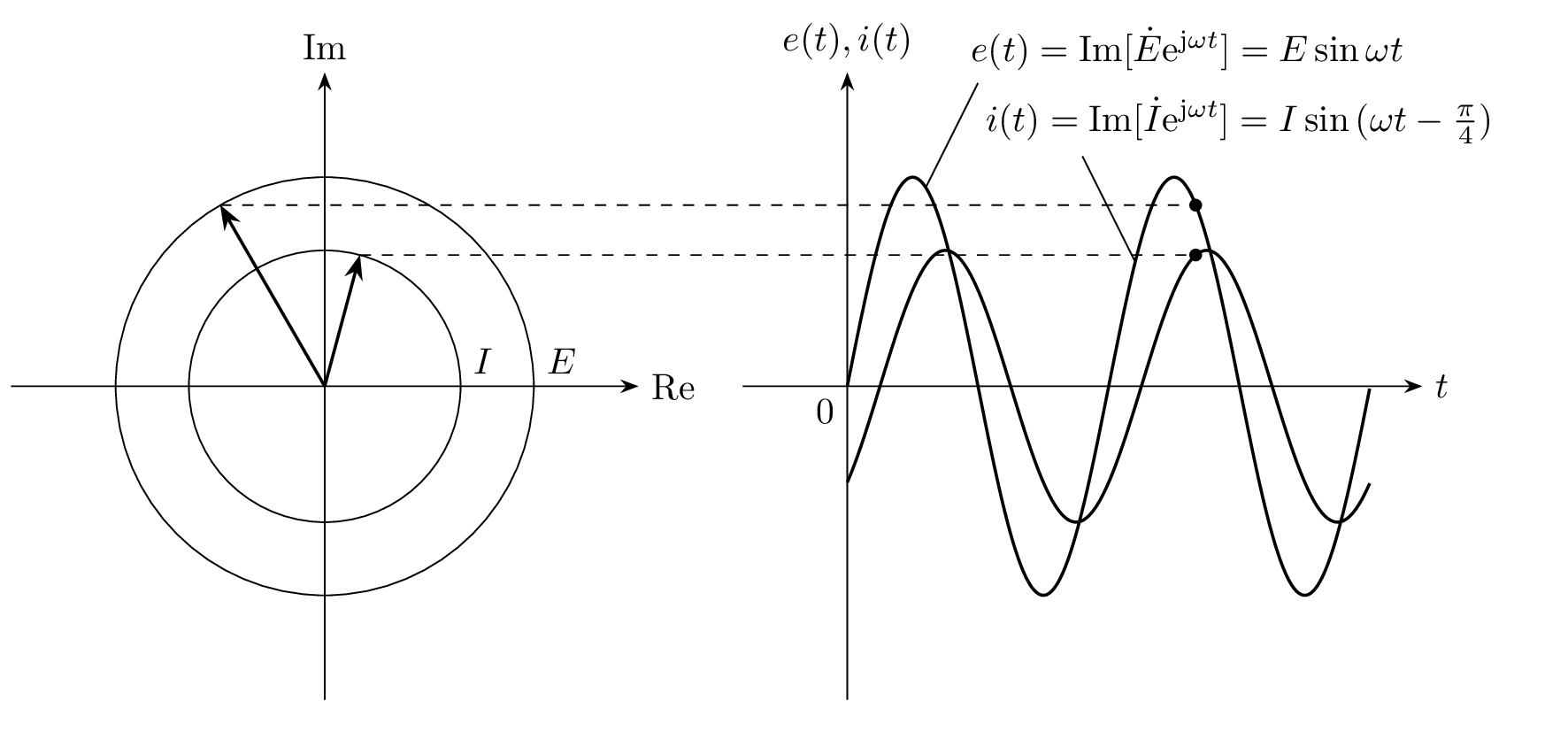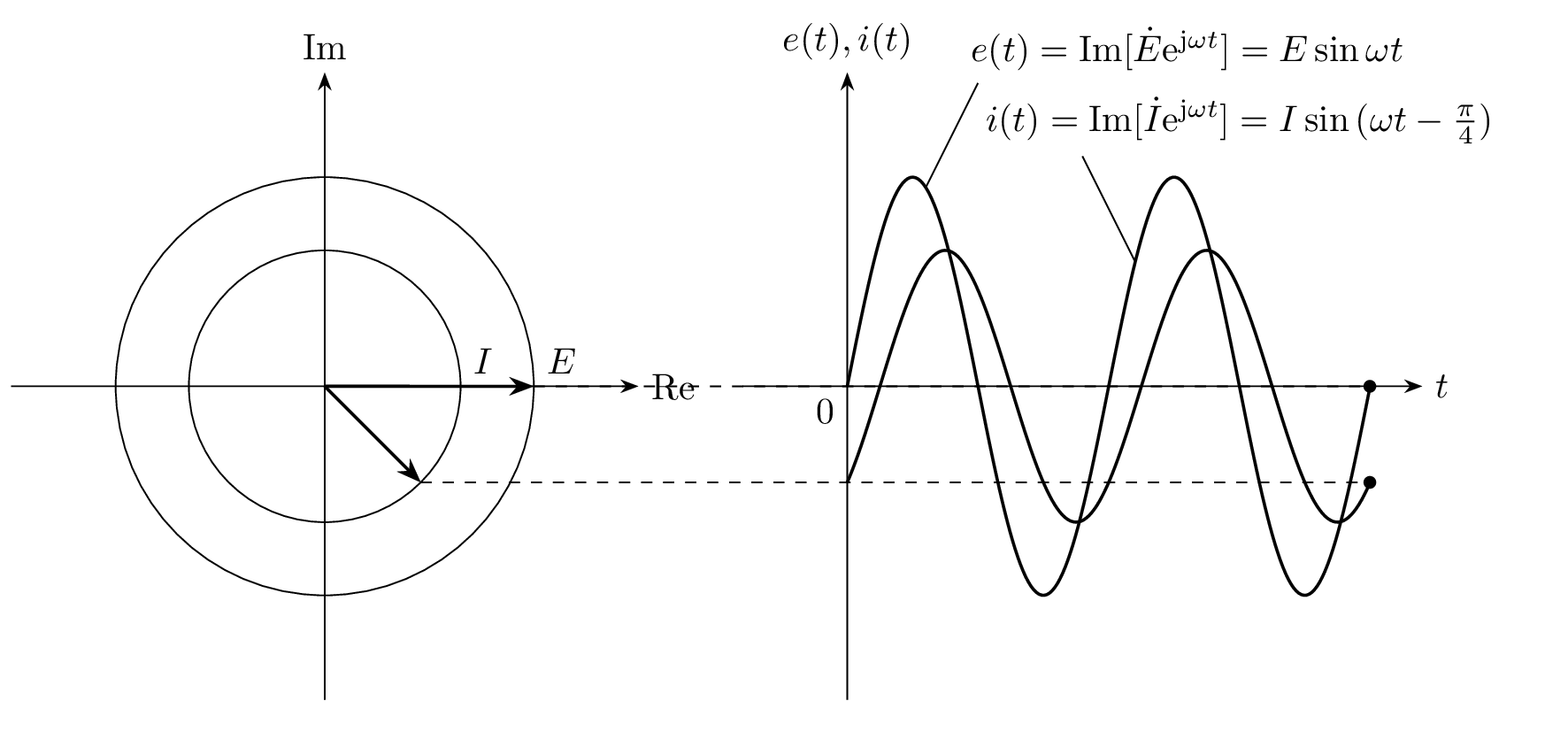
フェーザ \dot{E}, \dot{I} と電源電圧 e(t) と回路に流れる電流 i(t) の対応を表した図(I=|\dot{I}| とした)
(3) 抵抗・インダクタ・コンデンサの電圧のフェーザ \dot{V}_R, \dot{V}_L, \dot{V}_C および瞬時値 v_R(t), v_L(t), v_C(t) を求めてください。
答え
各素子の電圧のフェーザは次式で与えられます。
\begin{align*}
\dot{V}_R &= R\dot{I} = 100 \mathrm{e}^{-\mathrm{j}\frac{\pi}{4}} \left( = 100\angle -\frac{\pi}{4}\right) \\
\dot{V}_L &= \mathrm{j}\omega L \dot{I} = 300 \mathrm{e}^{\mathrm{j}\frac{\pi}{4}} \left( = 300\angle \frac{\pi}{4}\right) \\
\dot{V}_C &= \frac{\dot{I}}{\mathrm{j}\omega C} = 200 \mathrm{e}^{-\mathrm{j}\frac{3\pi}{4}} \left( = 200\angle -\frac{3\pi}{4}\right)
\end{align*}
各素子電圧の瞬時値は電圧フェーザに \mathrm{e}^{\mathrm{j}\omega t} を乗算して虚部をとることで次式で与えられます。
\begin{align*}
v_R(t) &= \text{Im} \left[ \dot{V}_R \mathrm{e}^{\mathrm{j}\omega t} \right] = 100 \sin \left( \omega t - \frac{\pi}{4} \right) \\
v_L(t) &= \text{Im} \left[ \dot{V}_L \mathrm{e}^{\mathrm{j}\omega t} \right] = 300 \sin \left( \omega t + \frac{\pi}{4} \right) \\
v_C(t) &= \text{Im} \left[ \dot{V}_C \mathrm{e}^{\mathrm{j}\omega t} \right] = 200 \sin \left( \omega t - \frac{3\pi}{4} \right)
\end{align*}
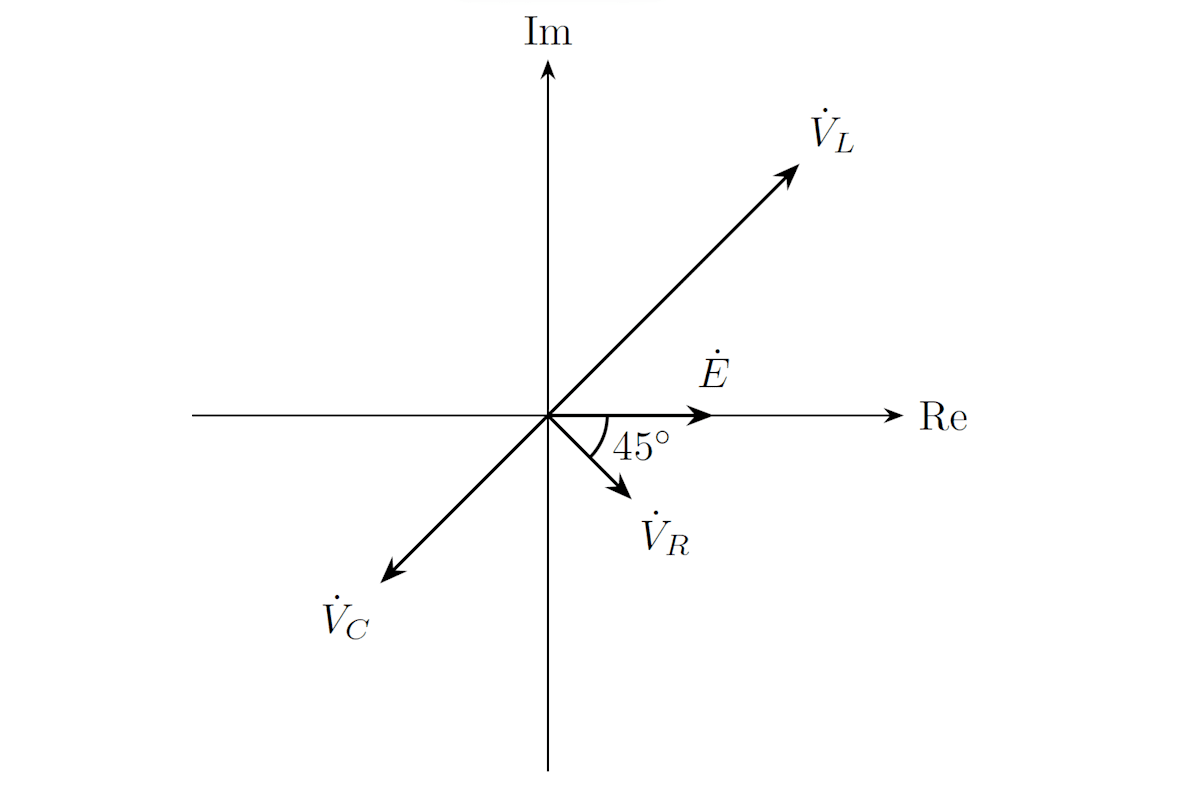
(4) 抵抗・インダクタ・コンデンサの電圧のフェーザ \dot{V}_R, \dot{V}_L, \dot{V}_C のフェーザ図を描いてください。ただし、電源電圧のフェーザ \dot{E} を実軸正方向としてください。
答え
\dot{V}_Rと \dot{V}_L、\dot{V}_Rと \dot{V}_C は直交します。また、フェーザ図上でも \dot{E} = \dot{V}_R + \dot{V}_L + \dot{V}_C が成立している必要があります。
参考文献
- 奥村浩士(2002)『エース電気回路理論入門(エース電気・電子・情報工学シリーズ)』朝倉書店 pp.83-89
- 黒木修隆(2012)『電気回路I』オーム社 pp.50-51
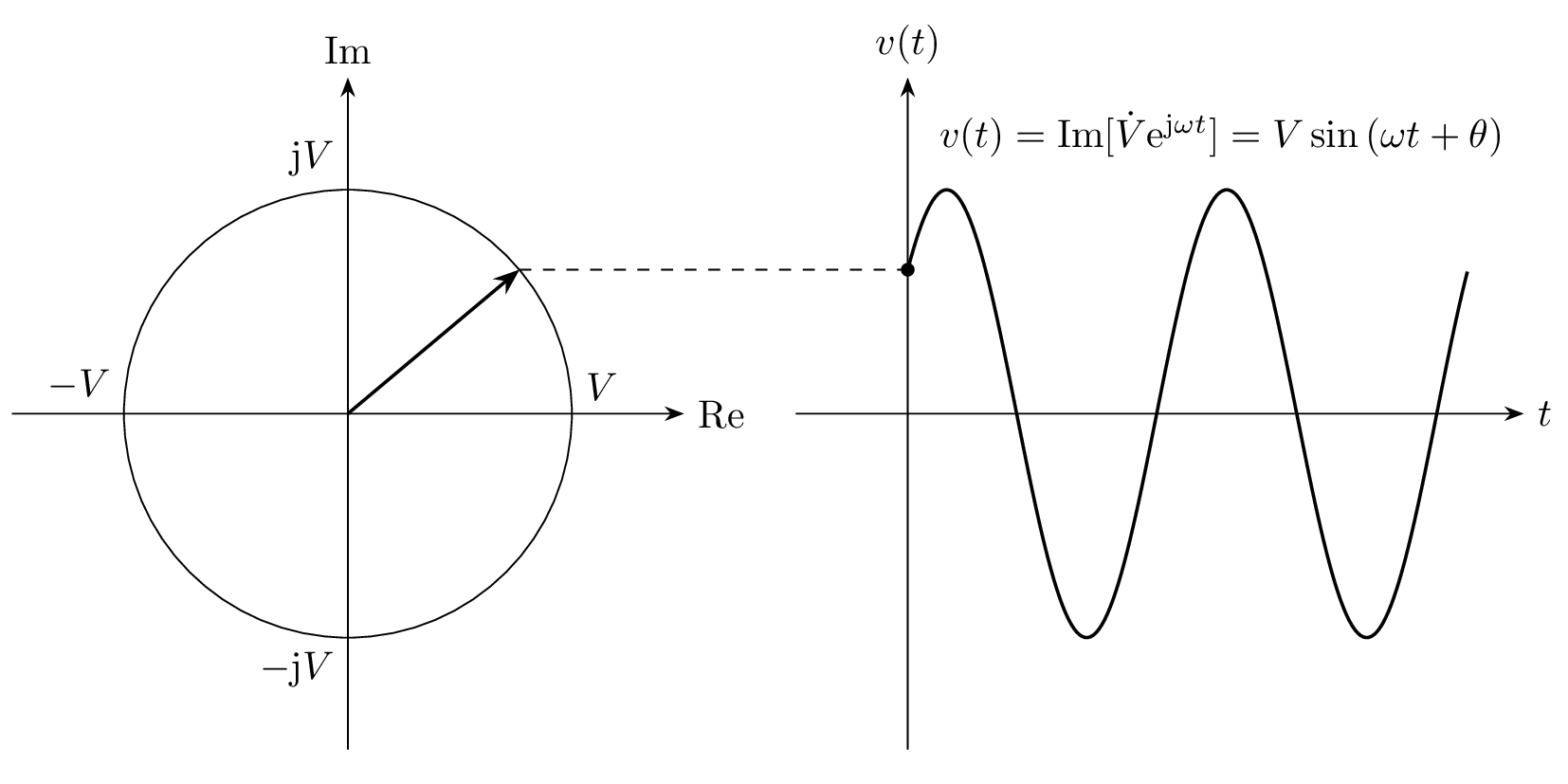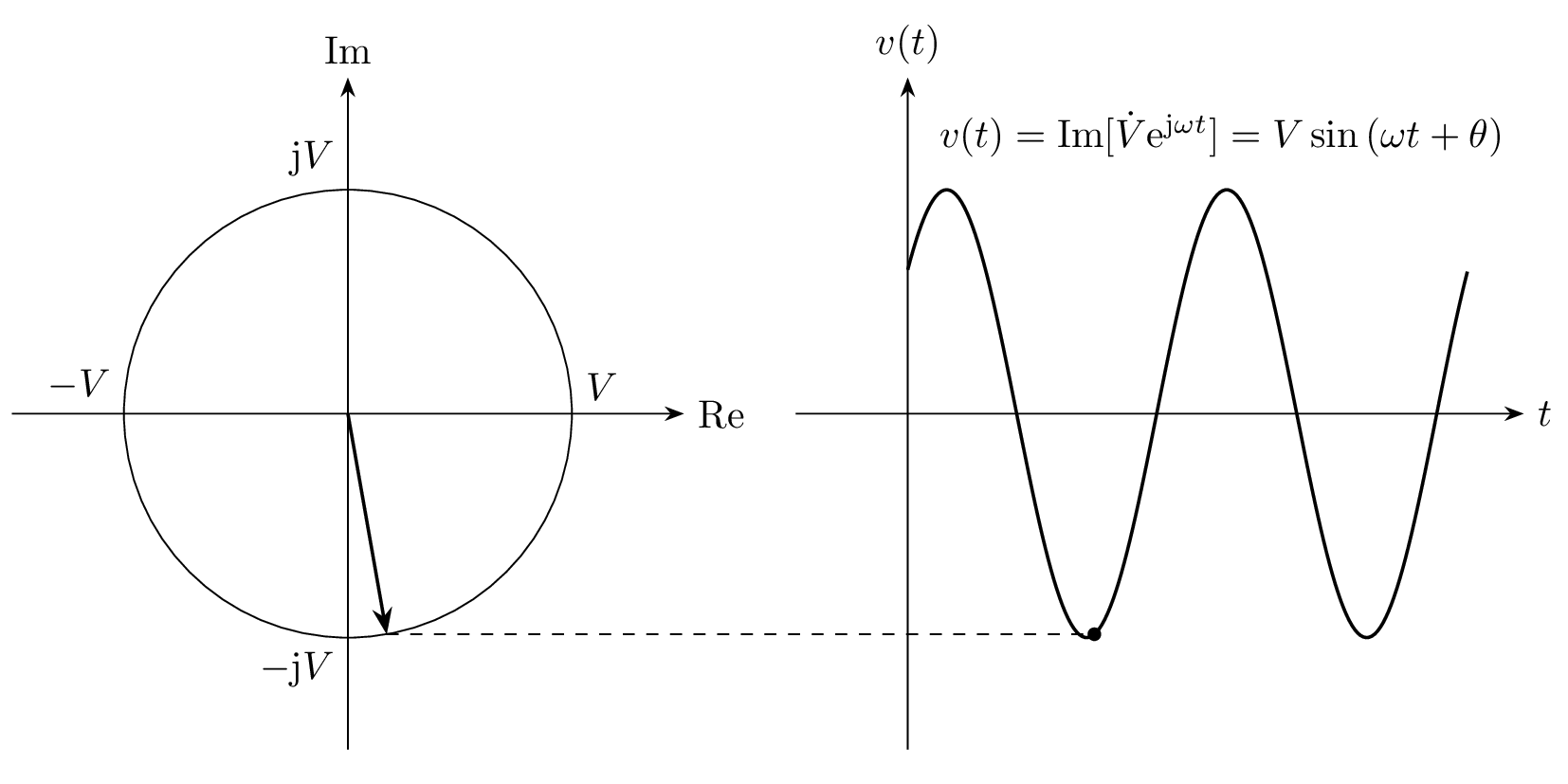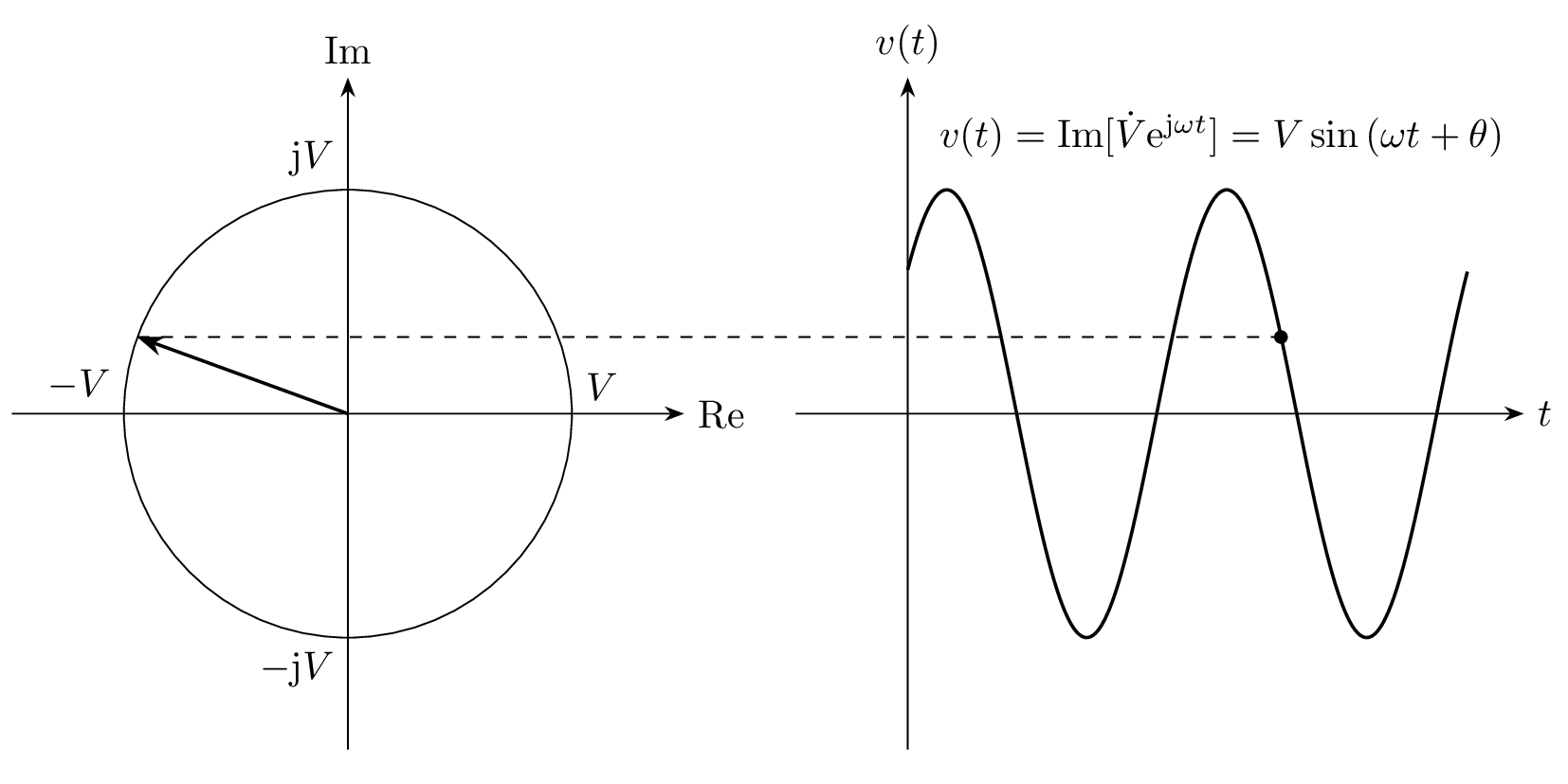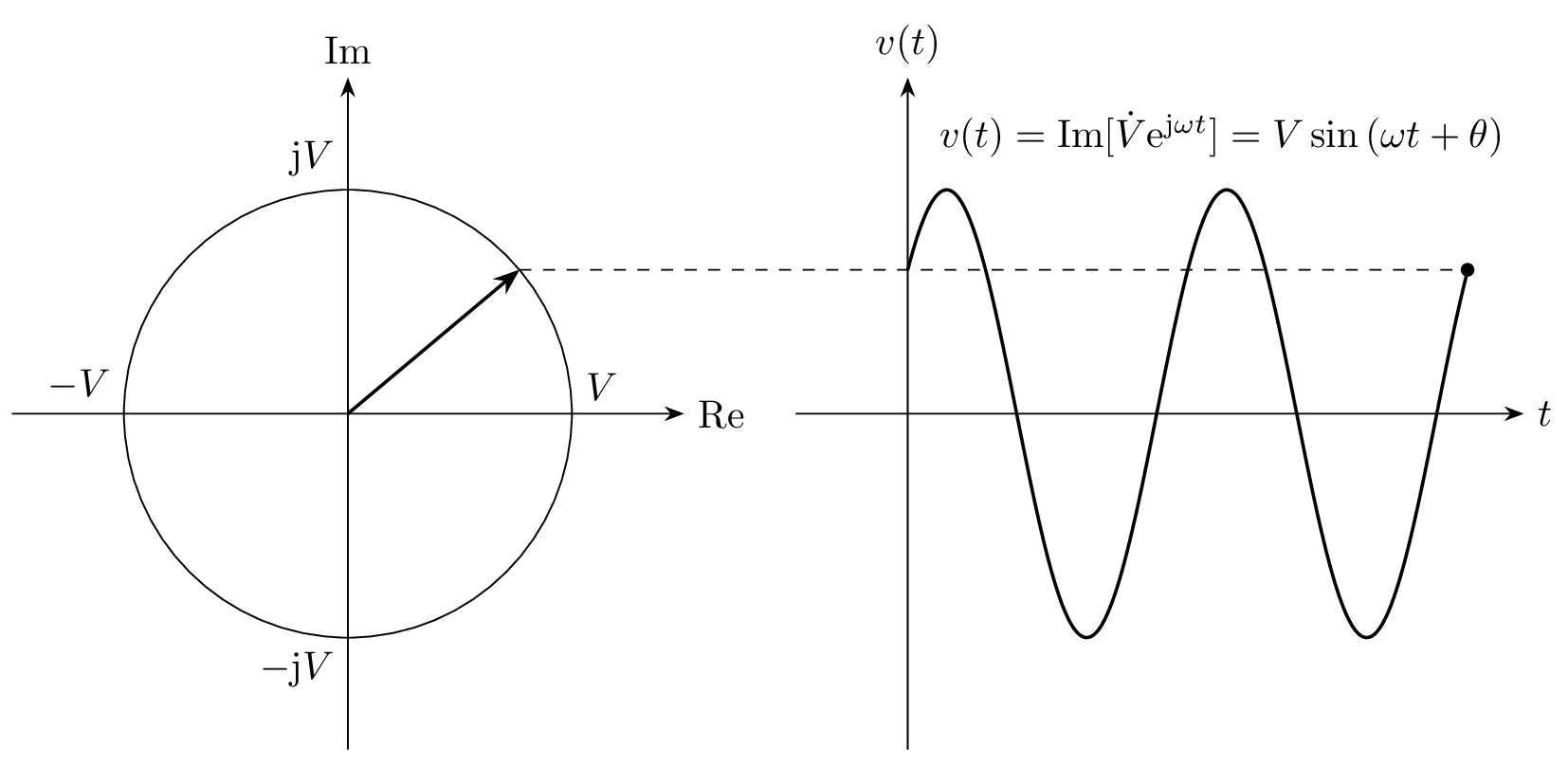

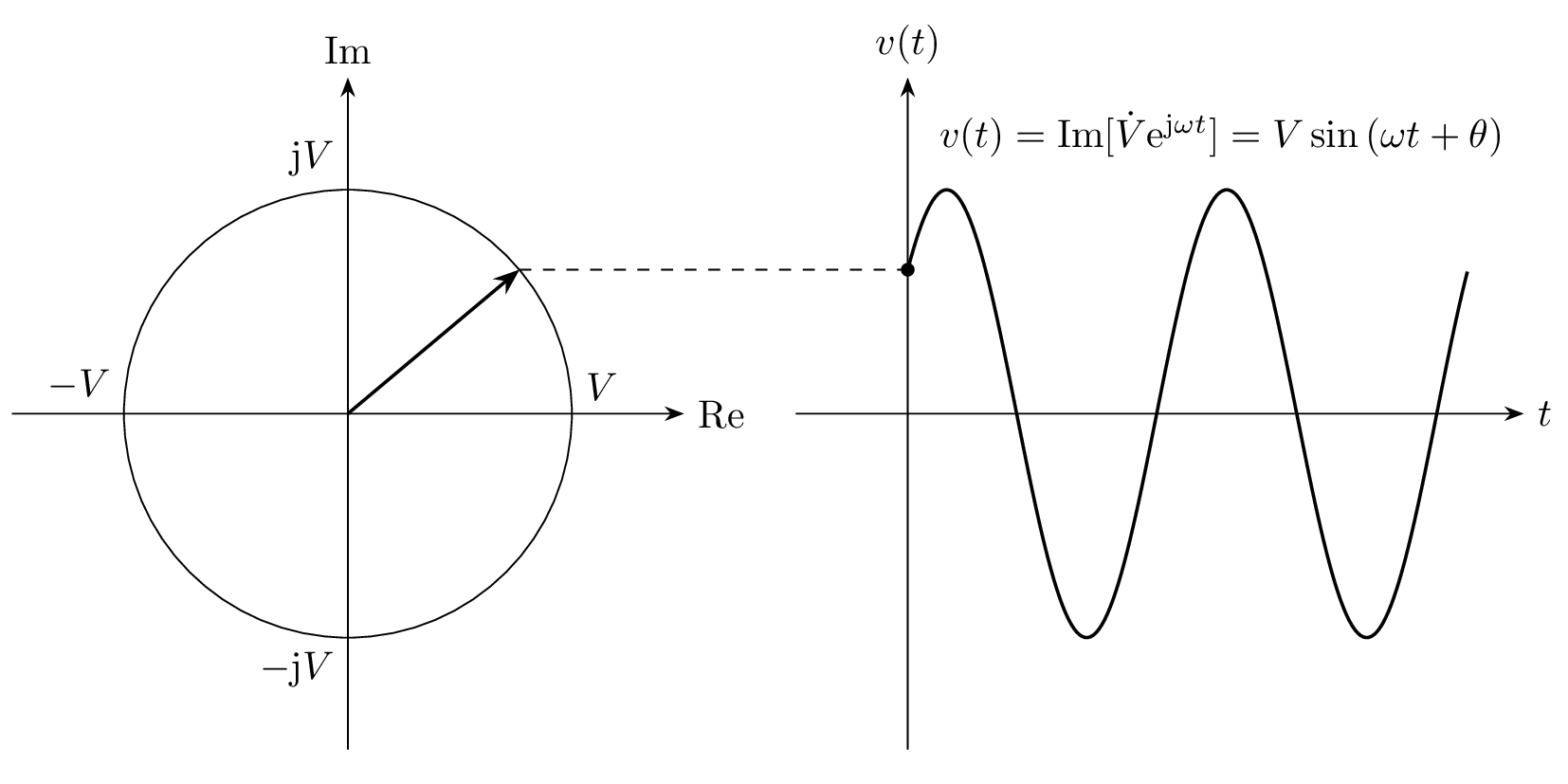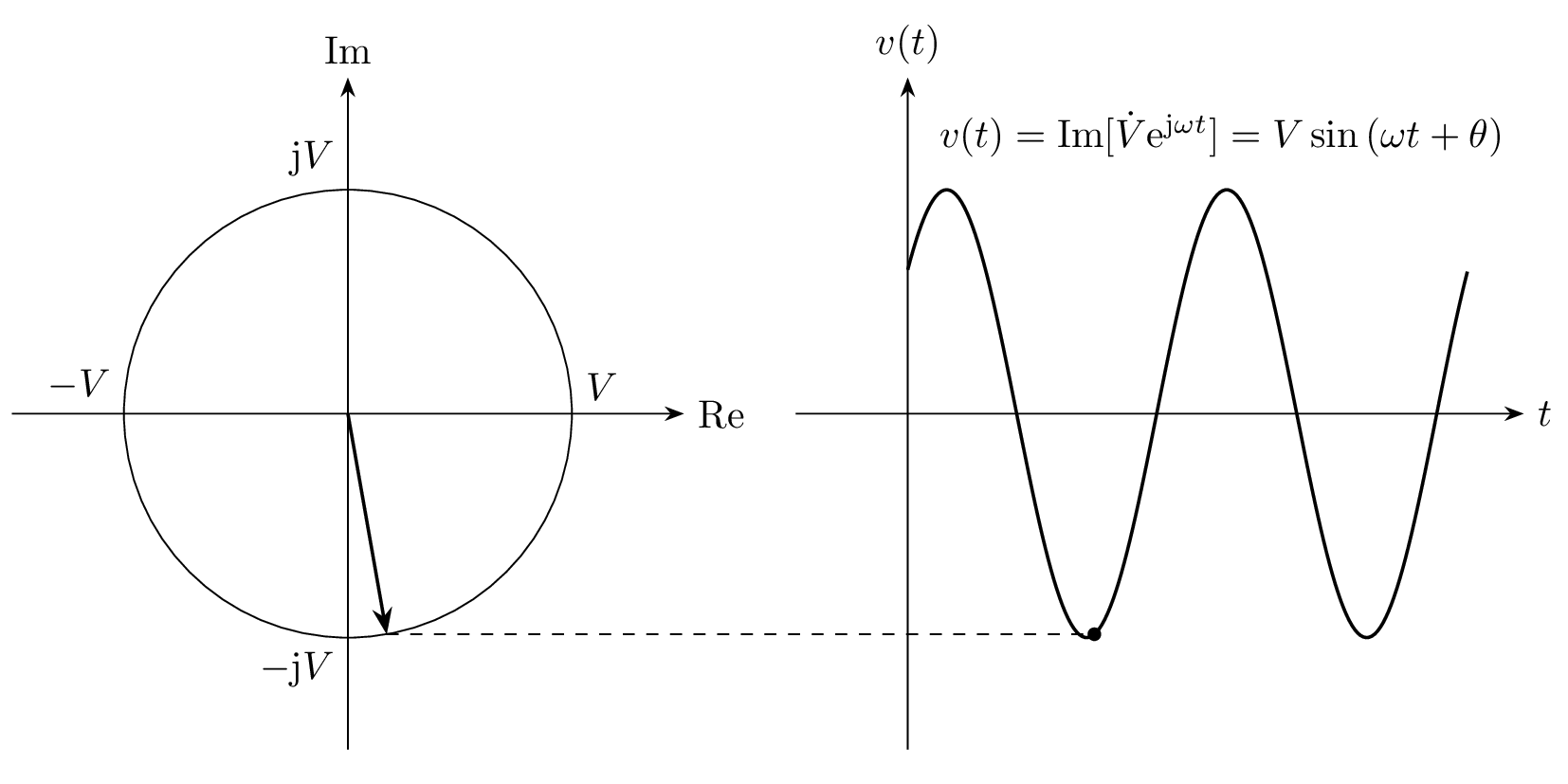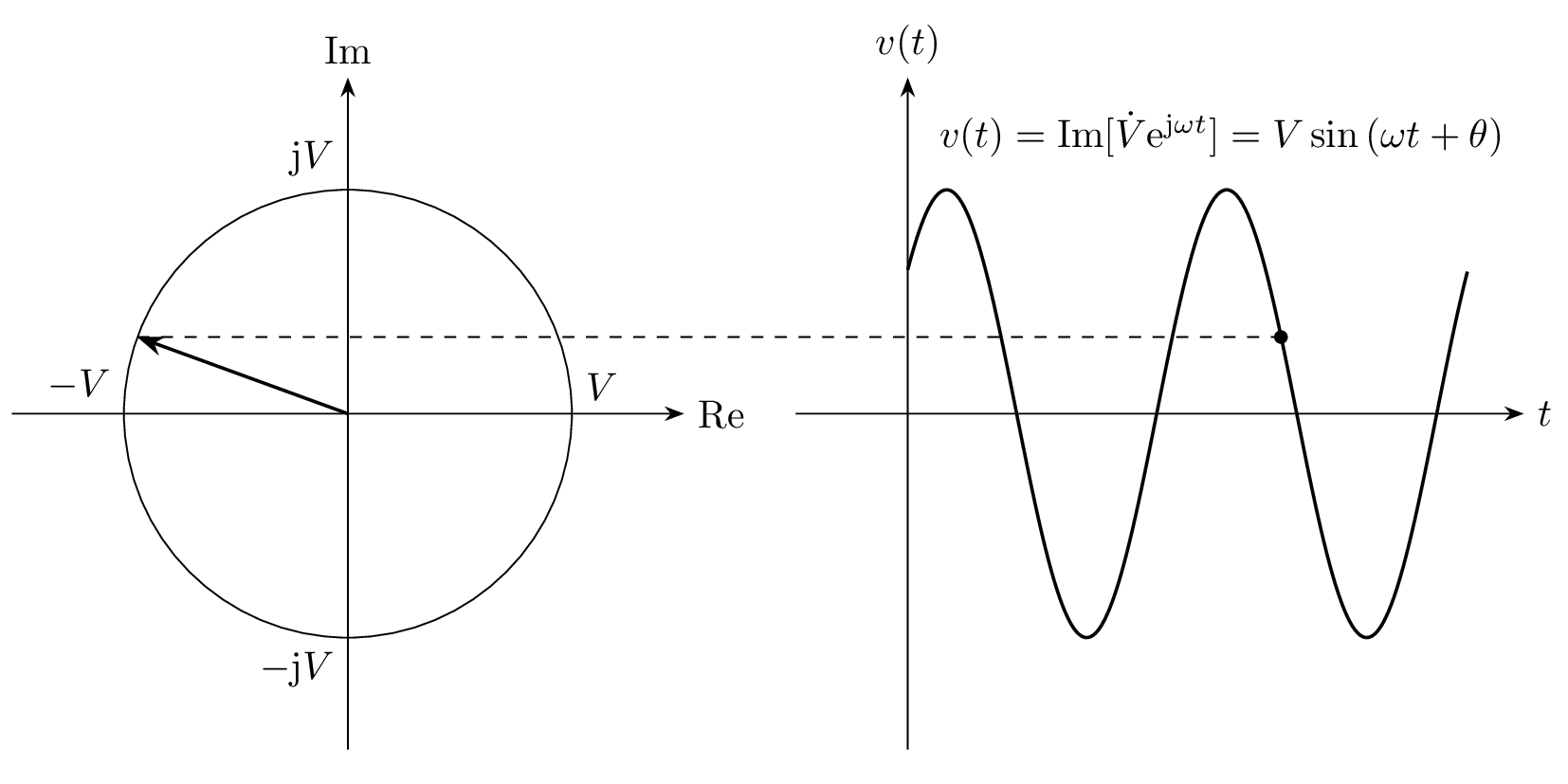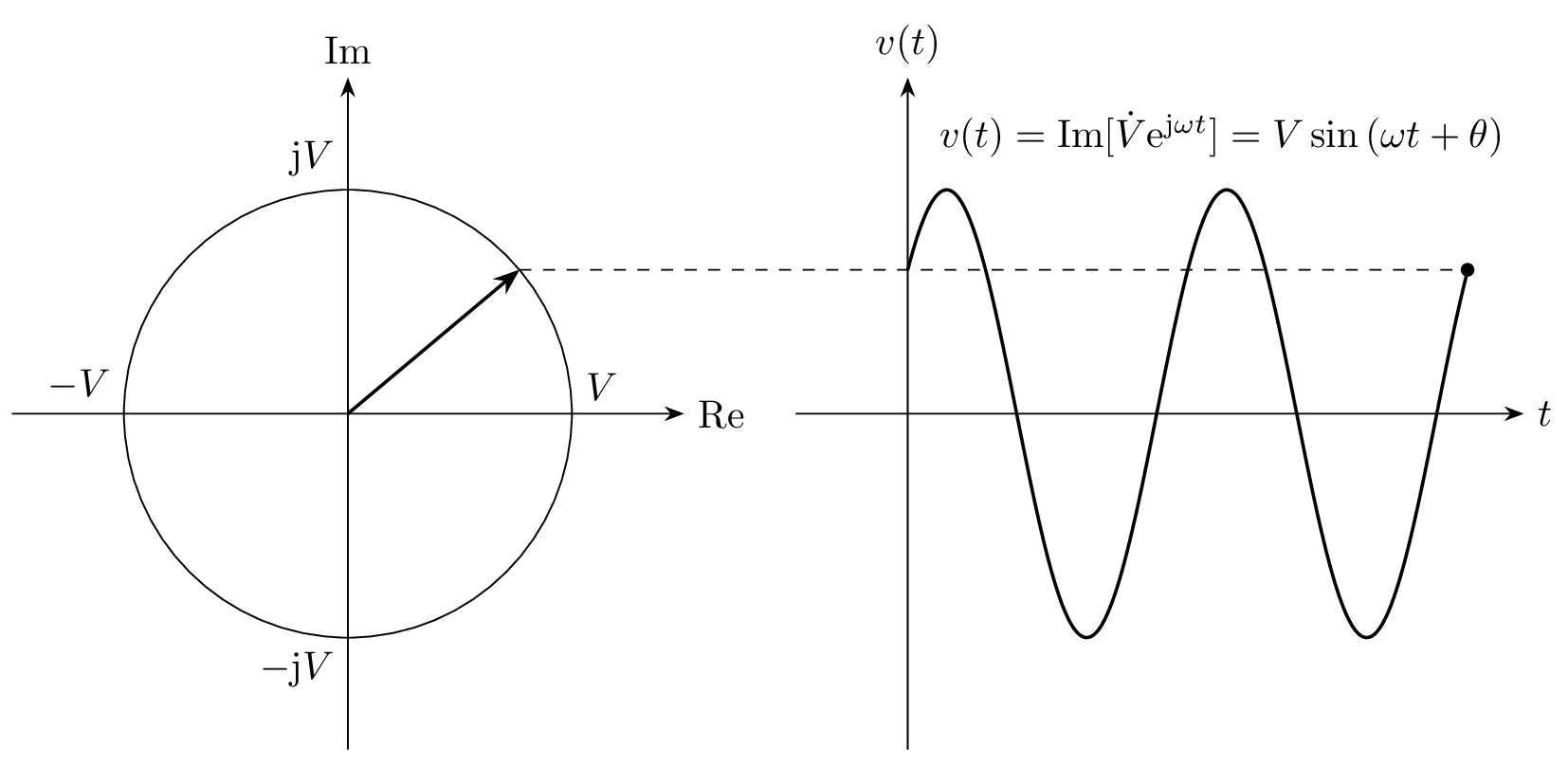


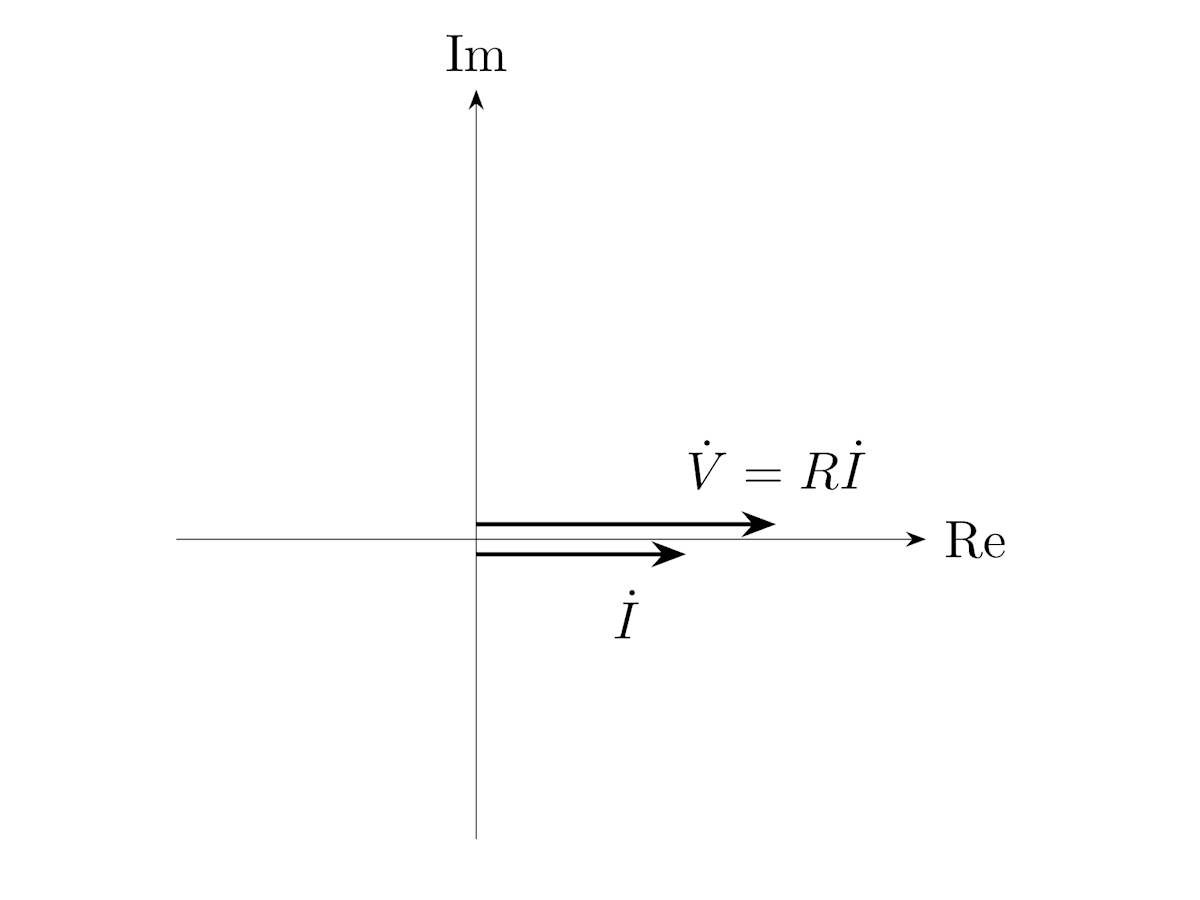
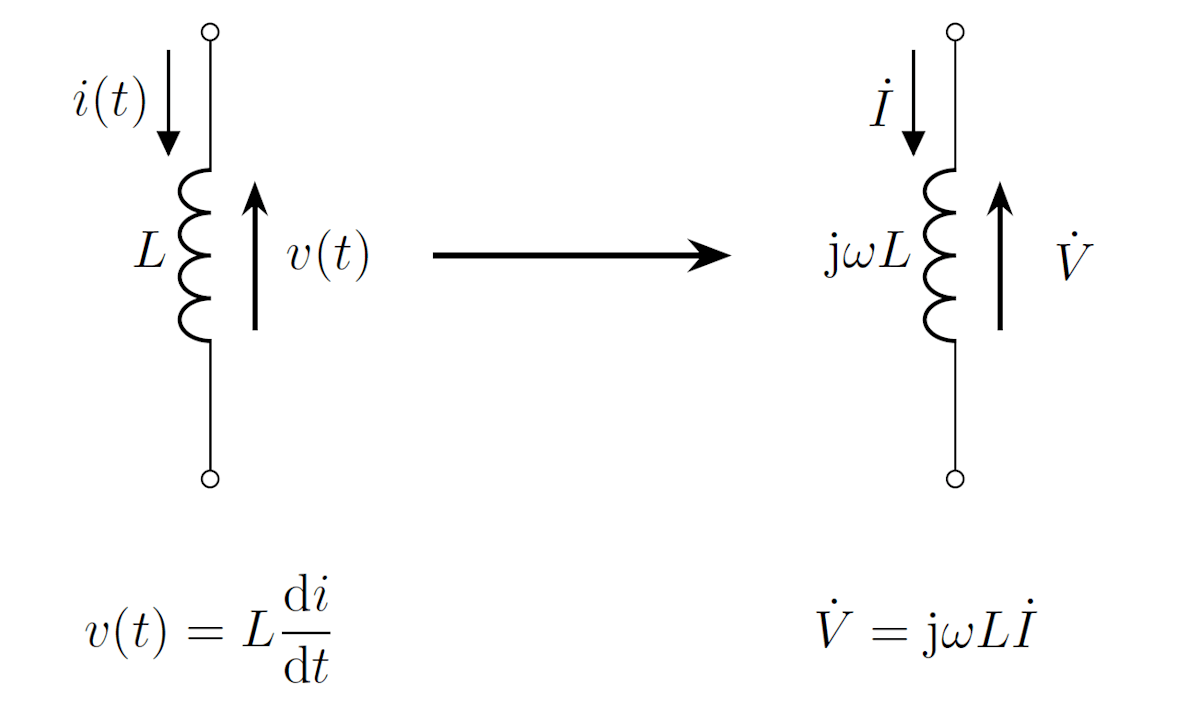
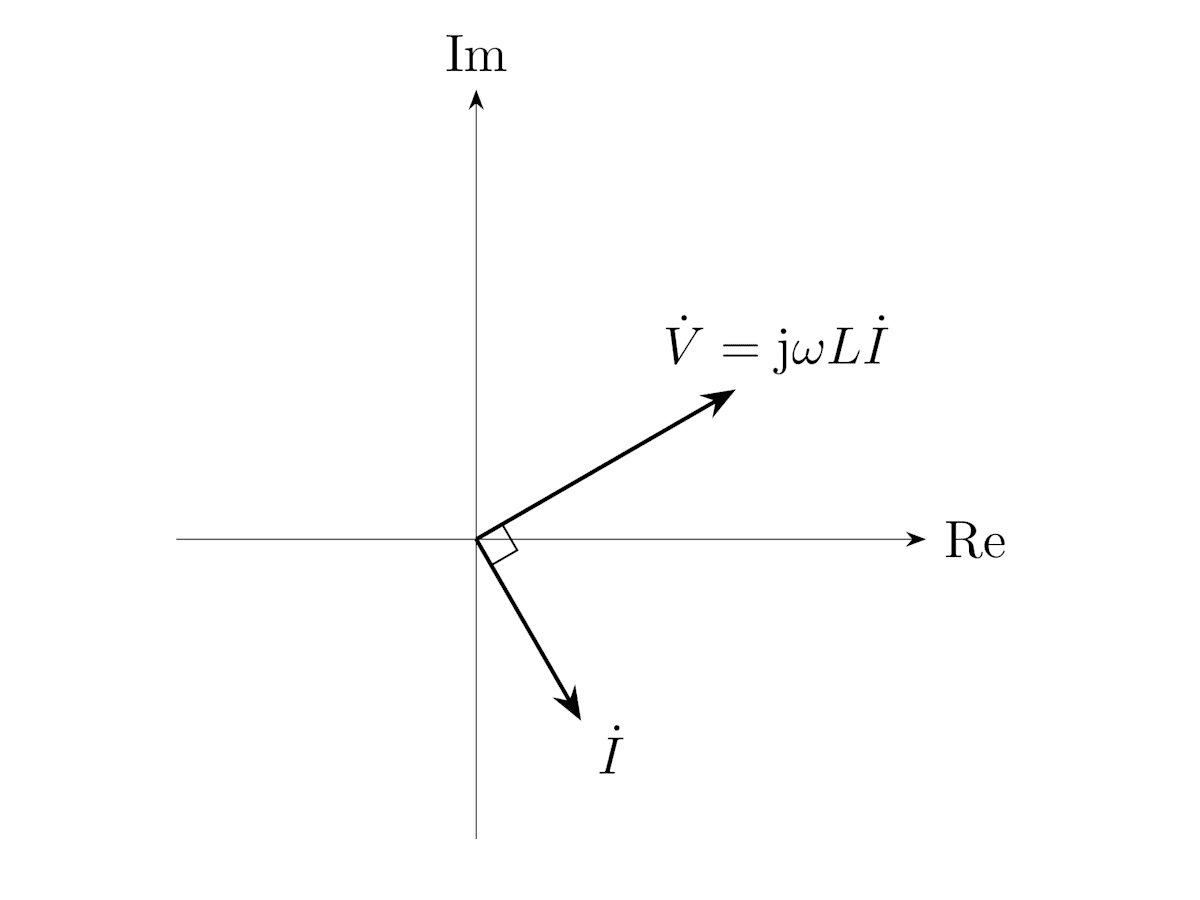
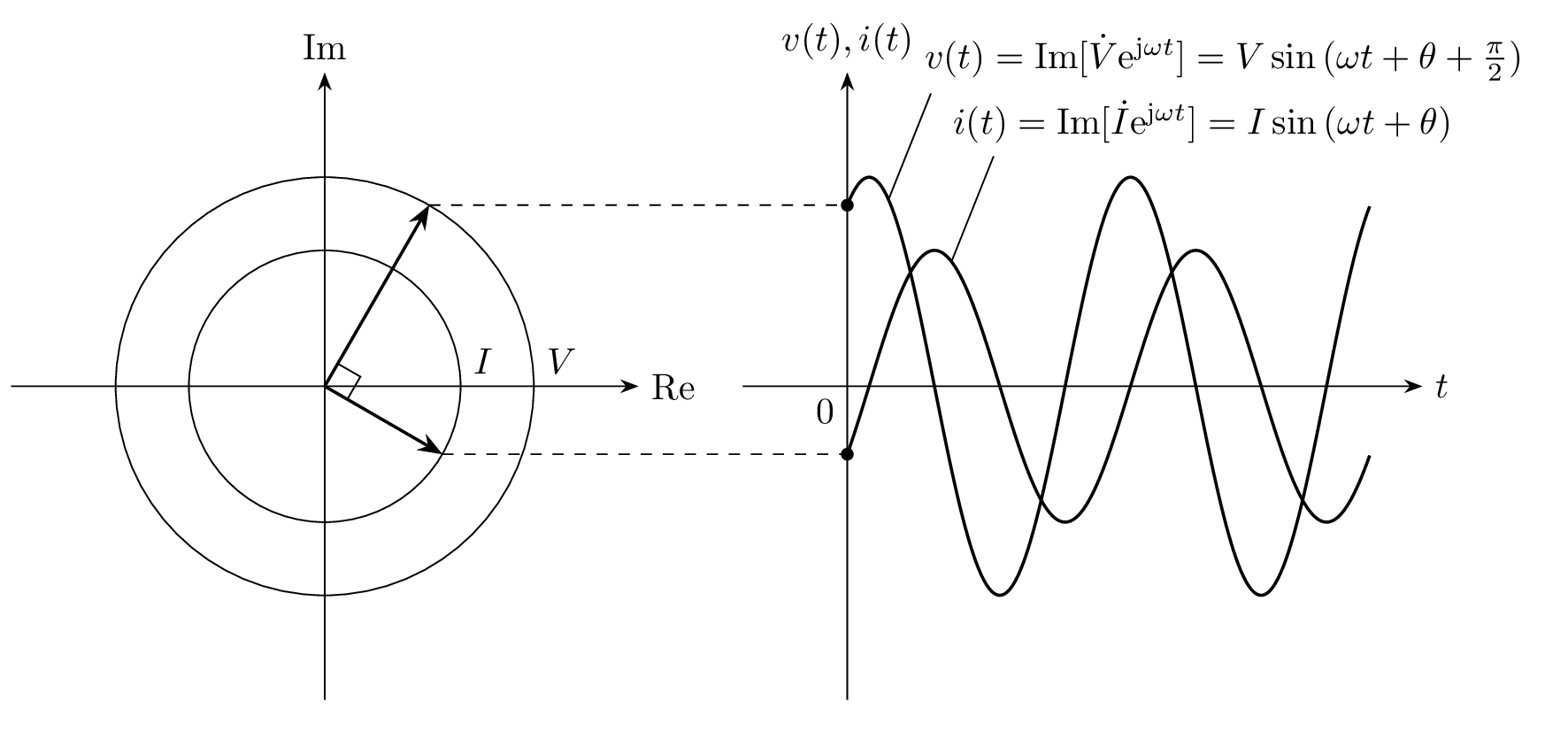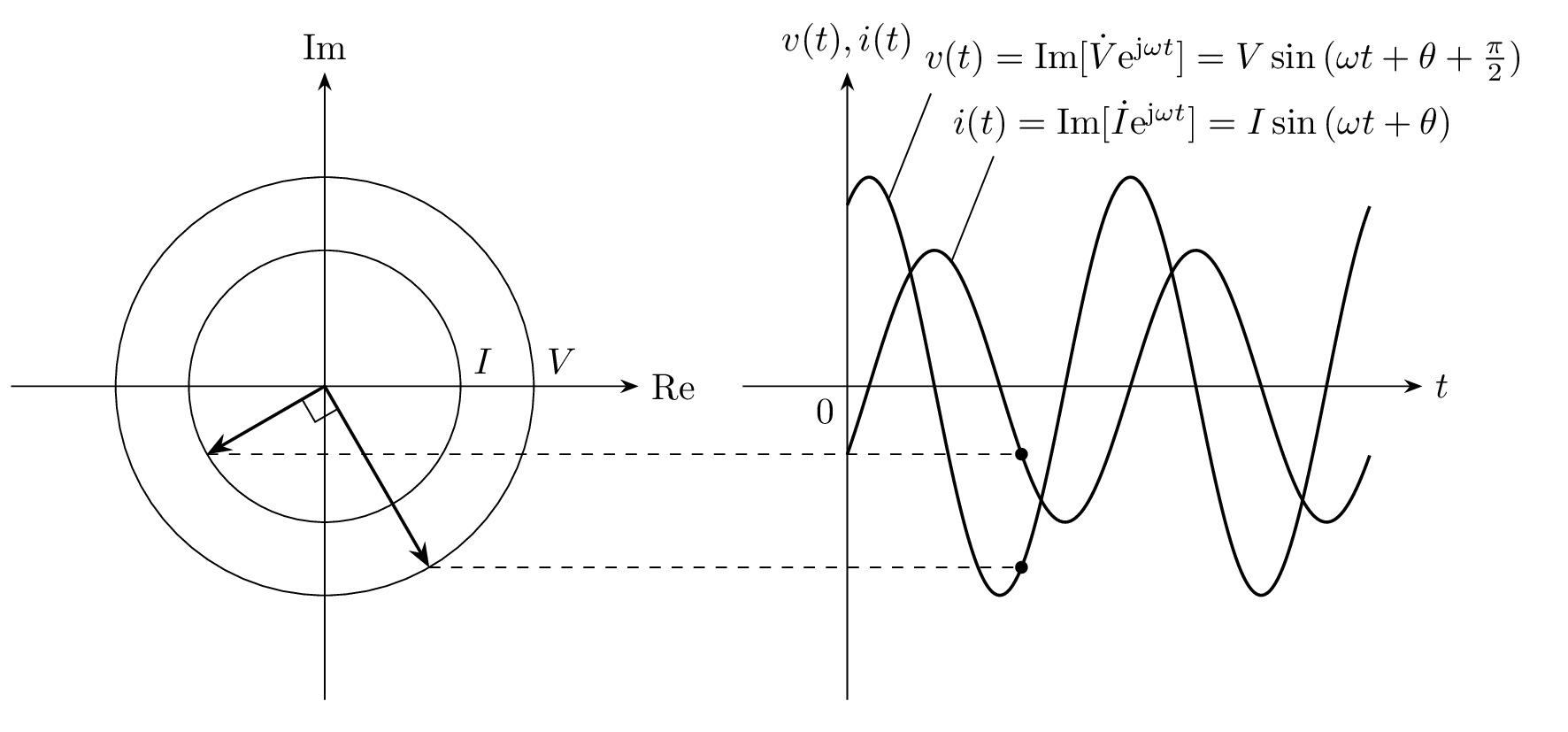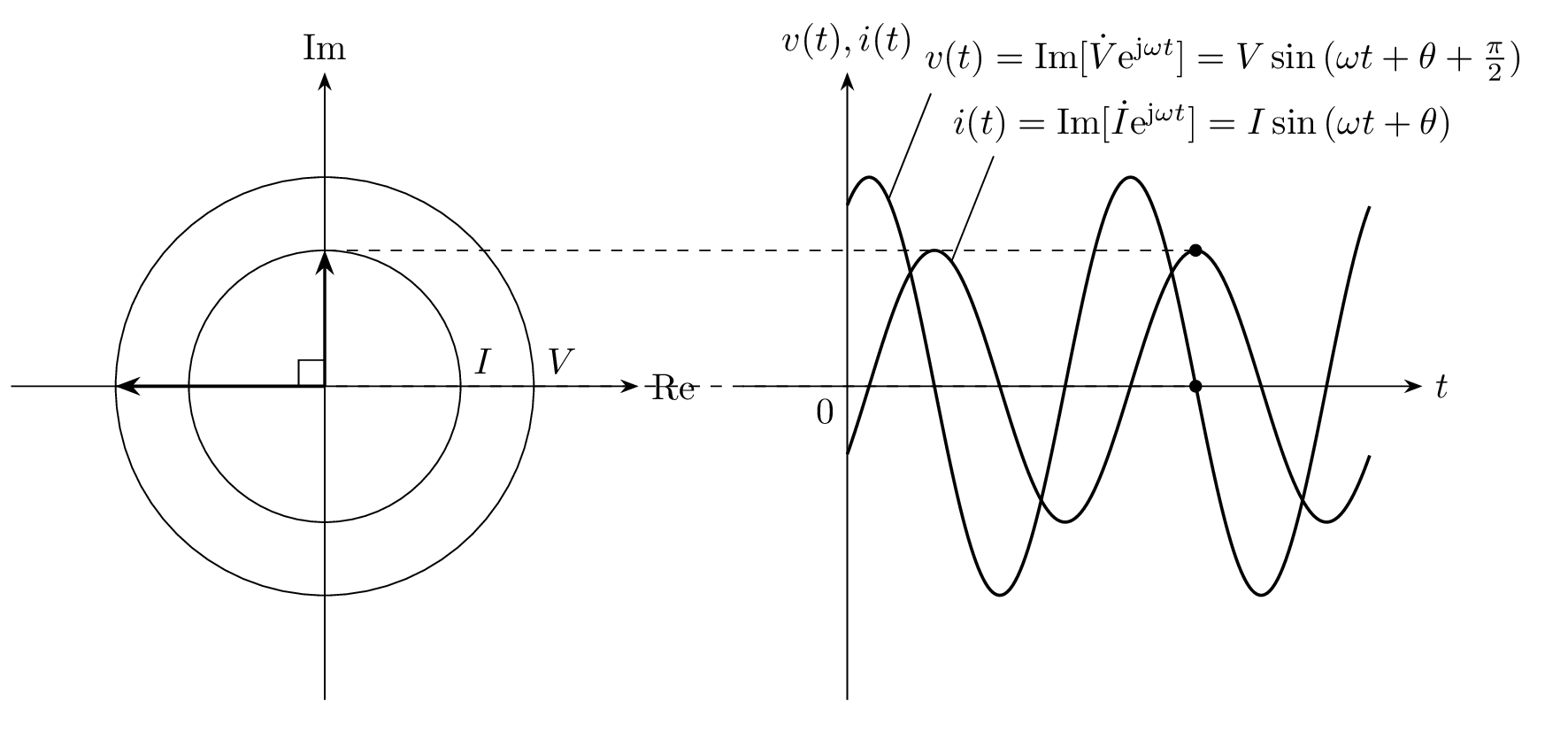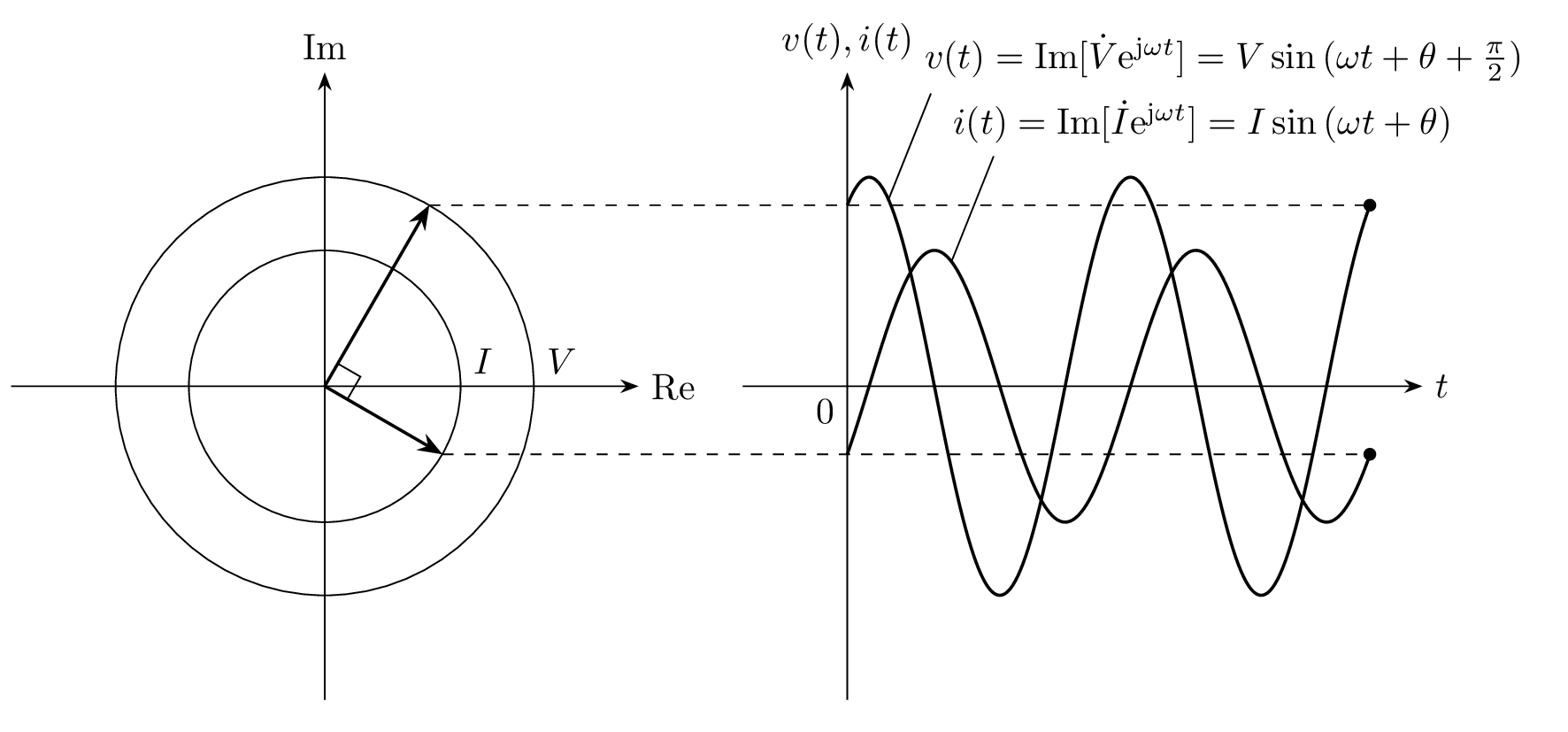
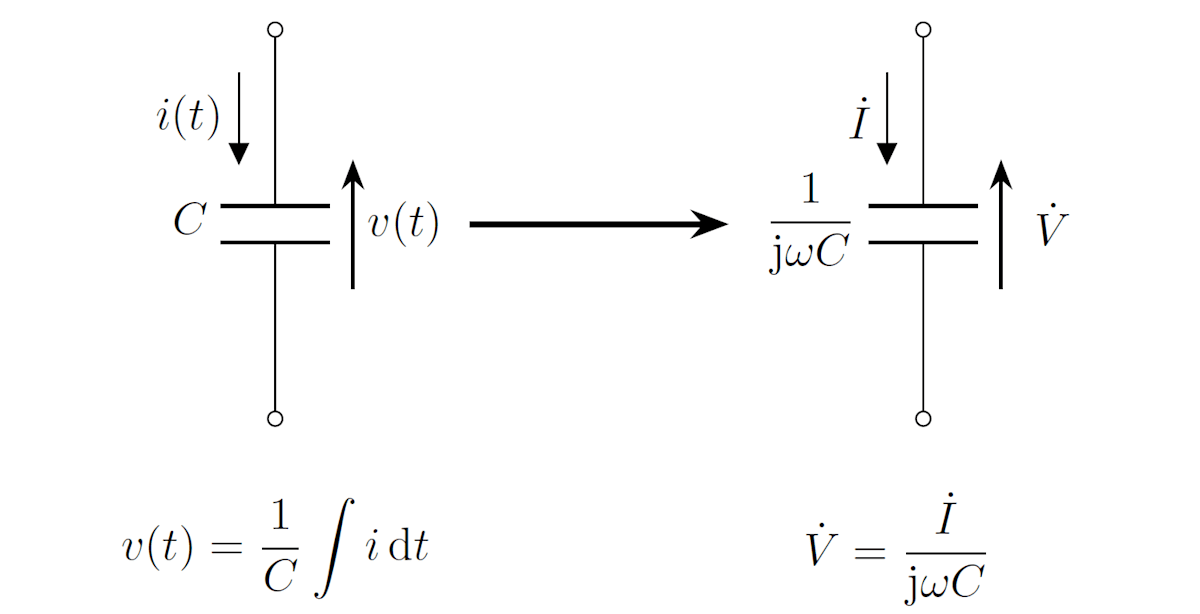
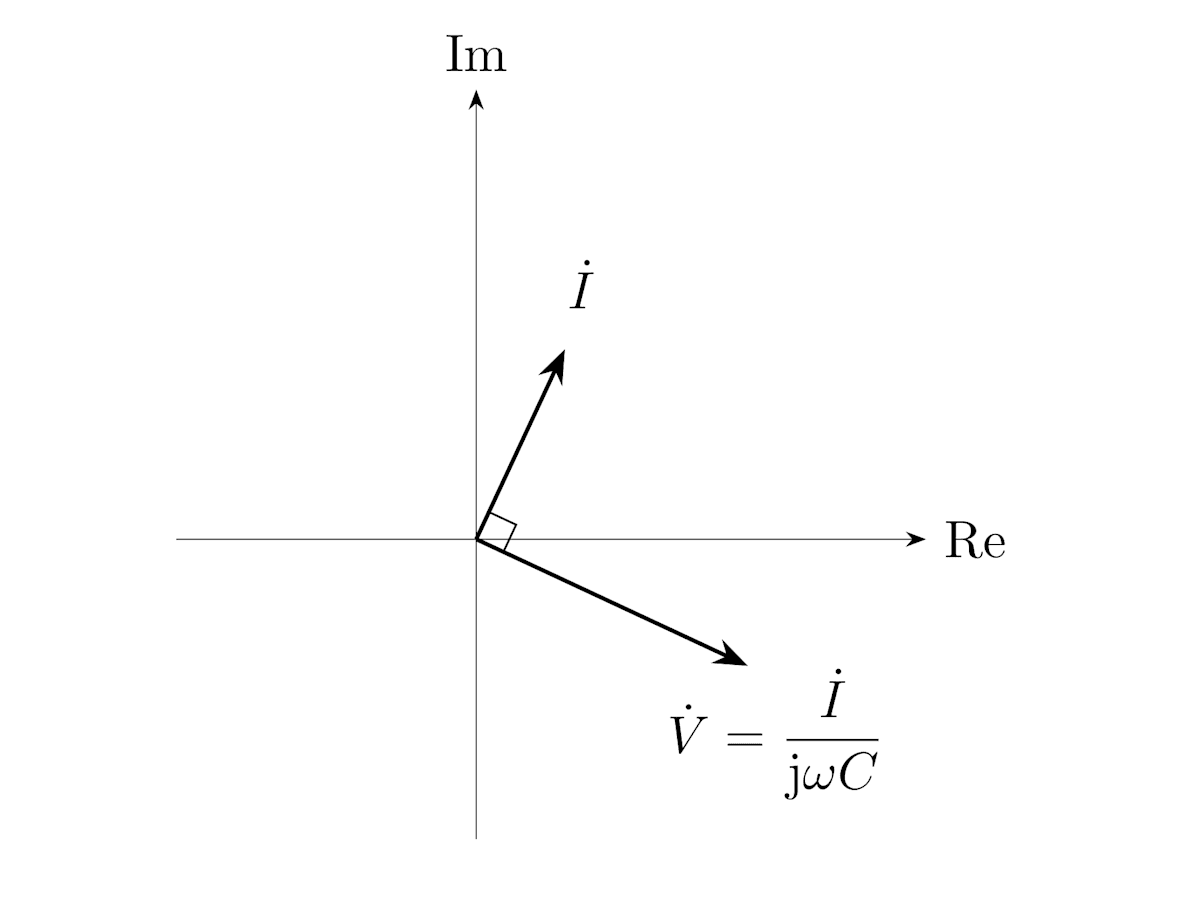






Discussion
フェーザ法をアニメーション表示で説明いただき、とても分かりやすいです。投稿をありがとうございました。
グラフも数式もとてもきれいに描かれており、勉強がしやすいので助かりました。