本記事の内容
本記事では以下の内容について解説します。
ノートンの定理による等価回路の作り方
ノートンの定理は簡潔に言えば、「回路上の任意の2端子を選んだ際、その間の短絡電流と開放コンダクタンスを基に等価な電流源を構成できる」 という定理です。
回路図を用いて説明します。下図のように、内部に電圧源や電流源を含む回路網を N_0、含まない回路網を N とします。
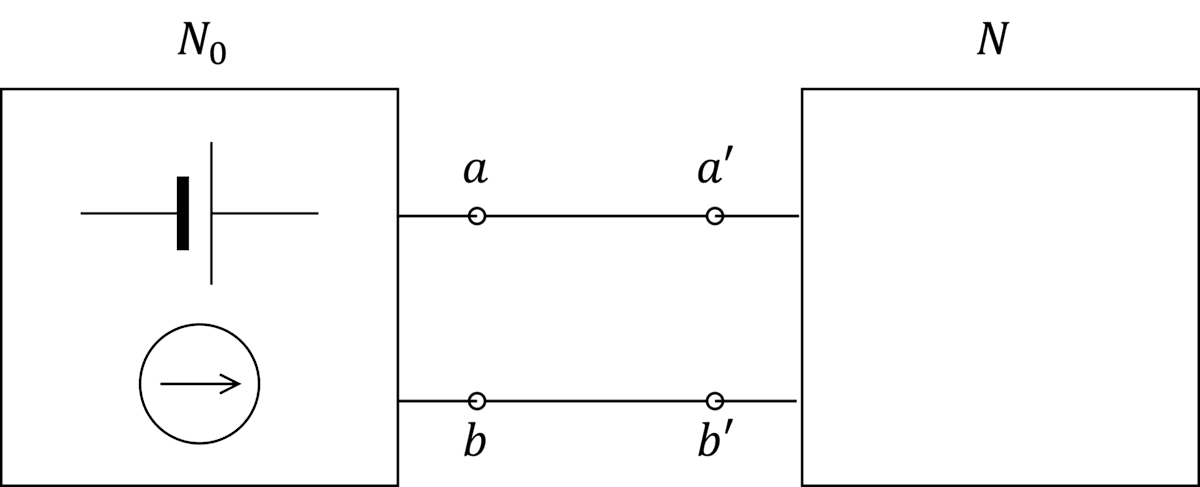
回路網 N_0 の電圧源を短絡し、電流源を開放したときの開放コンダクタンスを G_0、端子 a,b 間を短絡したときの N_0 における短絡電流を J_0 と定義します。

このとき、回路網 N_0 は短絡電流 J_0 と内部コンダクタンス G_0 で構成される等価電流源として表現できます。

例題
ノートンの定理を使った問題を2題示します。
例題1
下図の回路の抵抗 R に流れる電流 I を求めてみましょう。

端子 a,b を短絡したときの短絡電流 J_0 は次式で与えられます。
J_0 = \frac{E_1}{R_1} + \frac{E_2}{R_2}
開放コンダクタンス G_0 は、電圧源を短絡することで、次式で与えられます。
G_0 = \frac{1}{R_1} + \frac{1}{R_2}

したがって、等価回路は下図のようになります。

抵抗 R に流れる電流 I は次式で表されます。
\begin{align*}
I &= \frac{\frac{1}{R}}{G_0 + \frac{1}{R}} J_0 \\
&= \dfrac{1}{\frac{R}{R_1} + \frac{R}{R_2} + 1}\left(\dfrac{E_1}{R_1} + \dfrac{E_2}{R_2}\right)
\end{align*}
例題2
下図の回路の抵抗 R に流れる電流 I を求めてみましょう。

端子 a,b 間の短絡電流 J_0 は次式で与えられます。
開放コンダクタンス G_0 は次式で与えられます。

等価回路より、電流 I は次式で与えられます。
I = \frac{R_1}{R_1+R} J_0
ノートンの定理の証明
ノートンの定理の証明には、重ね合わせの原理を利用します。
内部に電源(電圧源や電流源)を含む回路網を N_0、電源を含まない回路を N とし、これらが端子 a, b で接続されているとします。

そして、回路網 N_0 の短絡電流を J_0 とおきます。

ここで、N_0 と N の間に電流 J_0 の電流源を接続した、下図の回路を考えます。

たとえ電流源を2つ配置したとしても、電流則に従えば、回路網 N に流れる電流 I は変わりません。したがって、上の回路は元の回路と同じ動作となります。
ここで、この回路に重ね合わせの原理を適用します。

左図の回路は、回路網 N 側に接続した電流源を開放したものです。一方、右図の回路は、その他のすべての電圧源を短絡、電流源を開放したものです。
左図の回路において、回路網 N に流れる電流は、短絡電流が J_0 であったことから、0\,\mathrm{A} になります。
したがって、右図の回路において回路網 N に流れる電流は、元の回路におけるそれと等しくなります。このため、この回路を解析することで、元の回路における回路網 N の電圧および電流を求めることが可能です。












Discussion