逆ラプラス変換
逆ラプラス変換の定義
時刻 t の関数 f(t) のラプラス変換(Laplace transform)F(s) は次式で定義されます。
F(s) = \mathcal{L}[f(t)] = \int_0^{\infty} f(t)\mathrm{e}^{-st} \mathrm{d}t
ただし、f(t) = 0 \, (t < 0) を満たし、s は s = \sigma + \mathrm{j}\omega (\sigma および \omega は実数) なる複素数で、ラプラス変換 F(s) は複素数全体で定義されます。
逆ラプラス変換(inverse Laplace transform) は次式で定義されます。
f(t) = \mathcal{L}^{-1}[F(s)] = \frac{1}{2\pi \mathrm{j}} \int_{\sigma-\mathrm{j}\infty}^{\sigma+\mathrm{j}\infty} F(s)\mathrm{e}^{st} \mathrm{d}s \tag{1}
逆ラプラス変換 (1) の右辺にある積分はブロムウィッチ積分(Bromwich integral) と呼ばれます。
逆ラプラス変換の計算方法
ラプラス変換 F(s) から元の実関数 f(t) を計算する方法は2つあります。
-
部分分数分解によって典型的なラプラス変換の形に持っていく
-
ブロムウィッチ積分を求める
1つ目の方法を適用する場合は、典型的なラプラス変換の形を覚えておく必要があります。一方、2つ目の方法はラプラス変換表に載っていないような関数に対しても適用できますが、複素解析に慣れている必要があります。本記事では、1つ目の方法である、部分分数分解によって逆ラプラス変換を求める方法を扱います。
典型的なラプラス変換を以下の表にまとめました。本記事では、この表に記載されているラプラス変換のみを扱います。
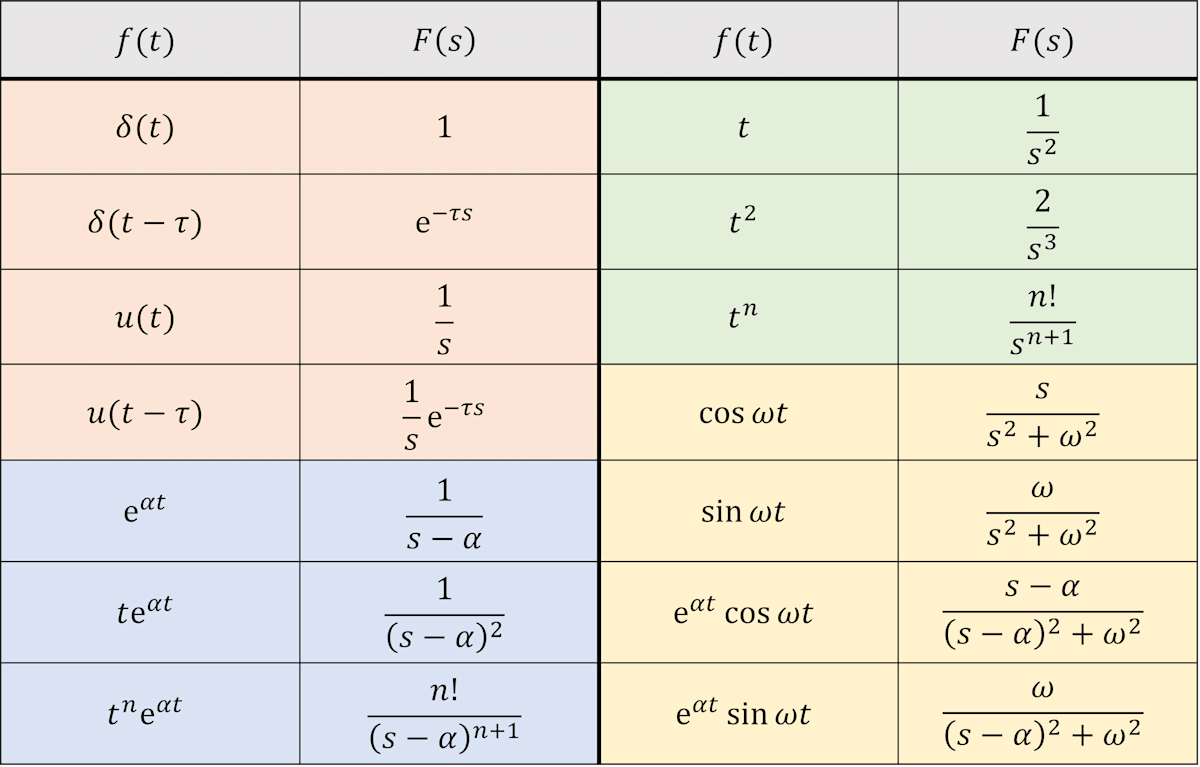
ラプラス変換表
部分分数分解による逆ラプラス変換の計算
ラプラス変換 F(s) の分母・分子がそれぞれ s に関する多項式 M(s), N(s) で表され、なおかつ分母の次数が分子の次数より大きい場合を考えます。
部分分数分解を行う際、M(s) = 0 の根が重要になり、これを F(s) の極(pole) といいます。また、その極が n 重根のとき、これをその極の位数(order) といいます。本記事では「n 位の極」のように呼びます。
例えば、M(s) = (s + 2)(s - 1)^3 のとき、s = -2 は 1 位の極、s = 1 は 3 位の極となります。
極と位数によって、部分分数分解の手続きが異なります。本記事では以下のように場合分けします。
- すべて1位の極
- 2位以上の極を含む
- 複素数の極を含む
すべて1位の極
具体例として、次式のラプラス変換の部分分数分解を考えます。
F(s) = \frac{s + 3}{(s + 1)(s + 2)}
F(s) の極は s = -1, -2 であり、それぞれ 1 位の極です。この部分分数分解を
F(s) = \frac{A}{s + 1} + \frac{B}{s + 2}
とおきます。ここで A, B はある定数です。A は F(s)(s + 1) に s = -1 を代入することで求められます。なぜなら、
F(s)(s + 1) = A + \frac{B}{s + 2}(s + 1) \xrightarrow{s = -1} A
のように第2項が 0 となるからです。B についても同様に考えれば、A, B はそれぞれ次式で与えられます。
A = F(s)(s + 1)\big|_{s = -1} = \left.\frac{s + 3}{s + 2}\right|_{s=-1} = 2
B = F(s)(s + 2)\big|_{s = -2} = \left.\frac{s + 3}{s + 1}\right|_{s = -2} = -1
以上より、ラプラス変換 F(s) の部分分数分解が求まりました。
F(s) = \frac{2}{s + 1} - \frac{1}{s + 2}
ラプラス変換表より、求めるラプラス逆変換 f(t) は次式で与えられます。
f(t) = 2\mathrm{e}^{-t} - \mathrm{e}^{-2t} \quad (t \geq 0)
2位以上の極を含む
具体例として、次式のラプラス変換の部分分数分解を考えます。
F(s) = \frac{4}{(s + 1)^2 (s + 3)}
F(s) の極は s = -1, -3 であり、それぞれ 2 位と 1 位の極です。この部分分数分解を
F(s) = \frac{A}{s + 1} + \frac{B}{(s + 1)^2} + \frac{C}{s + 3} \tag{2}
とおきます。ここで、A, B, C はある定数です。B, C に関しては、極がすべて 1 位のときと同様にして、
B = F(s)(s + 1)^2 |_{s = -1} = \left.\frac{4}{s + 3} \right|_{s = -1} = 2
C = F(s)(s + 3) |_{s = -3} = \left.\frac{4}{(s + 1)^2} \right|_{s = -3} = 1
と求められます。A についても同様に (s+1) を乗算すると
F(s)(s + 1) = A + \frac{B}{s + 1} + \frac{C}{s + 3}(s + 1)
となります。この場合、s = -1 を代入すると第2項の分母が 0 になってしまうため、この方法では A を求めることができません。
A の求め方として2つ紹介します。
- 係数比較法
- 微分を利用する方法
係数比較法
式 (2) の両辺に (s + 1)^2(s + 3)、つまり F(s) の分母をかけると、
\begin{align}
4 &= A(s + 1)(s + 3) + 2(s + 3) + (s + 1)^2 \notag \\
\Leftrightarrow \quad 4 &= (A + 1)s^2 + (4A + 4)s + (3A + 7) \notag
\end{align}
が得られます。この式は任意の s について成立する恒等式なので、各項の係数を調べることで A = -1 と求められます。
微分を利用する方法
2 つ目は、微分による方法です。まず、F(s) に (s + 1)^2 をかけると
(s + 1)^2 F(s) = A(s + 1) + B + \frac{C}{s + 3}(s + 1)^2
となります。両辺を s で微分すると、
\frac{\mathrm{d}}{\mathrm{d}s}\left\{(s + 1)^2 F(s)\right\} = A + \frac{\mathrm{d}}{\mathrm{d}s}\left\{\frac{C}{s + 3}(s + 1)^2\right\}
を得ます。右辺第2項については (s + 1) の項が残るので、s = -1 を代入すると 0 になります。一方、左辺について考えると、
\begin{align}
A = \left.\frac{\mathrm{d}}{\mathrm{d}s}\left\{(s + 1)^2 F(s)\right\}\right|_{s = -1} &= \frac{\mathrm{d}}{\mathrm{d}s}\left.\left(\frac{4}{s + 3}\right)\right|_{s = -1} \notag \\
&= -\left.\frac{4}{(s + 3)^2}\right|_{s = -1} \notag \\
&= -1 \notag
\end{align}
となり A = -1 と求められます。
以上より、ラプラス変換 F(s) の部分分数分解が求まりました。
F(s) = -\frac{1}{s + 1} + \frac{2}{(s + 1)^2} + \frac{1}{s + 3}
ラプラス変換表より、求めるラプラス逆変換 f(t) は次式で与えられます。
f(t) = -\mathrm{e}^{-t} + 2t\mathrm{e}^{-t} + \mathrm{e}^{-3t} \quad (t \geq 0)
複素数の極を含む
例えば、以下のラプラス変換の部分分数分解を考えます。
F(s) = \frac{s + 2}{(s + 1)\left(s^2 + 2s + 5\right)}
ここで、s^2 + 2s + 5 = 0 の根は s = -1 \pm 2\mathrm{j} で、F(s) は複素数の極を持ちます。
複素数の極を含む場合の解法として、以下の2つを紹介します。
- 複素数の極をそのまま扱う方法
- 実数係数でまとめて処理する方法
複素数の極をそのまま扱う方法
この方法は、F(s) の極がすべて1位のときと同様に部分分数分解を行う方法です。A, B, C を複素数の係数(実数の場合を含む)として部分分数分解を行うと、
F(s) = \frac{A}{s + 1} + \frac{B}{s + 1 - 2\mathrm{j}} + \frac{C}{s + 1 + 2\mathrm{j}}
となります。A, B, C はそれぞれ以下のように求められます。
A = F(s)(s + 1)\big|_{s = -1} = \left.\frac{s + 2}{s^2 + 2s + 5}\right|_{s = -1} = \frac{1}{4}
B = F(s)(s + 1 - 2\mathrm{j})\big|_{s = -1 + 2\mathrm{j}} = -\frac{1 + 2\mathrm{j}}{8}
C = F(s)(s + 1 + 2\mathrm{j})\big|_{s = -1 - 2\mathrm{j}} = -\frac{1 - 2\mathrm{j}}{8}
\mathrm{e}^{\mathrm{j}\alpha t} = \cos{\alpha t} + \mathrm{j}\sin{\alpha t} (\alpha は定数) であることに注意して、求めるラプラス逆変換 f(t) は次式で与えられます。
\begin{align*}
f(t) &= \frac{1}{4}\mathrm{e}^{-t} - \frac{1 + 2\mathrm{j}}{8}\mathrm{e}^{-(1 - 2\mathrm{j})t} - \frac{1 - 2\mathrm{j}}{8}\mathrm{e}^{-(1 + 2\mathrm{j})t} \\
&= \frac{1}{4}\mathrm{e}^{-t} - \frac{1}{8}\mathrm{e}^{-t}\left\{(1 + 2\mathrm{j})\mathrm{e}^{2\mathrm{j}t} + (1 - 2\mathrm{j})\mathrm{e}^{-2\mathrm{j}t}\right\} \\
&= \frac{1}{4}\mathrm{e}^{-t} - \frac{1}{4}\mathrm{e}^{-t}\cos 2t + \frac{1}{2}\mathrm{e}^{-t}\sin 2t
\end{align*}
実数係数でまとめて処理する方法
この方法は、複素数の極で部分分数分解をせずに実数係数のまま解く方法です。実数係数 A, D, E を用いて、以下のように F(s) を分解します。
F(s) = \frac{A}{s + 1} + \frac{Ds + E}{s^2 + 2s + 5} \tag{3}
第2項をこのように変形したのは、\mathrm{e}^{\alpha t}\cos \omega t, \, \mathrm{e}^{\alpha t}\sin \omega t のラプラス変換の形に持っていくことを狙っているためです。
\begin{align*}
\mathcal{L}[\mathrm{e}^{\alpha t}\cos \omega t] &= \frac{s - \alpha}{(s - \alpha)^2 + \omega^2} \\
\mathcal{L}[\mathrm{e}^{\alpha t}\sin \omega t] &= \frac{\omega}{(s - \alpha)^2 + \omega^2}
\end{align*}
A は先程と同様の方法で A = 1/4 と求められます。D, E は係数比較法により求めます。式 (3) の両辺に (s + 1)(s^2 + 2s + 5) を乗算して s に関する恒等式を得ます。
\begin{align*}
s + 2 &= A(s^2 + 2s + 5) + (Ds + E)(s + 1) \\
\Leftrightarrow \quad s + 2 &= (A + D)s^2 + (2A + D + E)s + (5A + E)
\end{align*}
係数を比較して、以下の連立方程式を得ます。
\begin{cases}
A + D = 0 \\
2A + D + E = 1 \\
5A + E = 2
\end{cases}
よって、D = -1/4, \, E = 3/4 と求められます。式 (3) に代入して、
F(s) = \frac{1}{4}\left(\frac{1}{s + 1} - \frac{s - 3}{s^2 + 2s + 5}\right)
を得ます。ここで、右辺第 2 項の分母を平方完成します。
\begin{align*}
\frac{s - 3}{s^2 + 2s + 5} &= \frac{s + 1 - 4}{(s + 1)^2 + 4} \\
&= \frac{s + 1}{(s + 1)^2 + 2^2} - 2\cdot\frac{2}{(s + 1)^2 + 2^2}
\end{align*}
第1項は \mathrm{e}^{-t}\cos 2t、第2項は -2\mathrm{e}^{-t}\sin 2t のラプラス変換に他なりません。これで、F(s) を典型的なラプラス変換の形に分解できたので、求めるラプラス逆変換 f(t) は次式で与えられます。
f(t) = \frac{1}{4}\mathrm{e}^{-t} - \frac{1}{4}\mathrm{e}^{-t}\left(\cos 2t - 2\sin 2t\right)
例題
各ラプラス変換 F(s) のラプラス逆変換 f(t) を求めてみましょう。
問1: 部分分数分解が不要な場合
F(s) = \frac{3}{s} + \frac{4}{s^2 + 4} + \frac{s + 7}{s^2 + 10s + 29}
答え
典型的なラプラス変換の形になるように変形します。
\begin{align*}
F(s) &= \frac{3}{s} + \frac{4}{s^2 + 4} + \frac{s + 7}{s^2 + 10s + 29} \\
&= \frac{3}{s} + 2\cdot\frac{2}{s^2 + 2^2} + \frac{s + 5}{(s + 5)^2 + 2^2} + \frac{2}{(s + 5)^2 + 2^2}
\end{align*}
ラプラス変換表を参照して、求めるラプラス逆変換 f(t) は次式で与えられます。
f(t) = 3 + 2\sin{2t} + \mathrm{e}^{-5t}\cos{2t} + \mathrm{e}^{-5t}\sin{2t}
問2: すべて1位の極の場合
F(s) = \frac{(s + 2)^2}{(s + 1)(s + 3)(s + 4)}
答え
実数係数をA,B,C として部分分数分解を行います。
F(s) = \frac{A}{s+1} + \frac{B}{s+3} + \frac{C}{s+4}
各係数は次式で与えられます。
\begin{align*}
A &= (s+1)F(s)|_{s=-1} = \frac{1}{6} \\
B &= (s+3)F(s)|_{s=-3} = -\frac{1}{2} \\
C &= (s+4)F(s)|_{s=-4} = \frac{4}{3}
\end{align*}
よって、求めるラプラス逆変換 f(t) は次式で与えられます。
f(t) = \frac{1}{6}\mathrm{e}^{-t} - \frac{1}{2}\mathrm{e}^{-3t} + \frac{4}{3}\mathrm{e}^{-4t}
問3: 2位以上の極を含む場合
F(s) = \frac{s^2 + s + 1}{(s + 2)^2(s + 3)}
答え
実数係数をA,B,C として部分分数分解を行います。
F(s) = \frac{A}{s+2} + \frac{B}{(s+2)^2} + \frac{C}{s+3}
B,C は次式で与えられます。
\begin{align*}
B &= (s+2)^2F(s)|_{s=-2} = 3 \\
C &= (s+3)F(s)|_{s=-3} = 7
\end{align*}
A は係数比較法により求めます。F(s) の両辺に (s+2)^2(s+3) を乗算して s に関する恒等式を得ます。
s^2 + s + 1 = (A+C)s^2 + (5A+B+4C)s + (6A+3B+4C)
係数を比較することで A=-6 と求められます。よって、部分分数分解は以下になります。
F(s) = -\frac{6}{s+2} + \frac{3}{(s+2)^2} + \frac{7}{s+3}
以上より、求めるラプラス逆変換 f(t) は次式で与えられます。
f(t) = -6\mathrm{e}^{-2t} + 3t\mathrm{e}^{-2t} + 7\mathrm{e}^{-3t}
(別解)係数 A は (s+2)^2 F(s) を s で微分したものに s=-2 を代入することでも求められます。(s+2)^2 F(s) の1階微分は次式で与えられます。
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d}s}\left\{(s+2)^2F(s)\right\} &= \frac{\mathrm{d}}{\mathrm{d}s}\left(\frac{s^2+s+1}{s+3}\right) \\
&= \frac{s^2+6s+2}{(s+3)^2}
\end{align*}
s=-2 を代入して A が求まります。
A = \left.\frac{\mathrm{d}}{\mathrm{d}s}\left\{(s+2)^2F(s)\right\}\right|_{s=-2} = \left.\frac{s^2+6s+2}{(s+3)^2}\right|_{s=-2} = -6
問4: 複素数の極を含む場合
F(s) = \frac{s + 2}{(s + 1)(s^2 + 4s + 8)}
答え
実数係数をA,B,C として部分分数分解を行います。
F(s) = \frac{A}{s+1} + \frac{Bs+C}{s^2+4s+8}
A は次式で与えられます。
A = (s+1)F(s)|_{s=-1} = \frac{1}{5}
B,C は係数比較法により求めます。F(s) の両辺に (s + 1)(s^2 + 4s + 8) を乗算して s に関する恒等式を得ます。
s + 2 = (A + B)s^2 + (4A + B + C)s + (8A + C)
係数を比較することで、以下の連立方程式を得ます。
\begin{cases}
A + B = 0 \\
4A + B + C = 1 \\
8A + C = 2
\end{cases}
これを解くことで B = -1/5, C = 2/5 と求められ、部分分数分解の結果は次式で表されます。
\begin{align*}
F(s) &= \frac{1}{5} \frac{1}{s+1} - \frac{1}{5} \frac{s-2}{s^2+4s+8} \\
&= \frac{1}{5} \frac{1}{s+1} - \frac{1}{5} \left\{\frac{s+2}{(s+2)^2+2^2} - 2\cdot\frac{2}{(s+2)^2+2^2}\right\}
\end{align*}
以上より、求めるラプラス逆変換 f(t) は次式で与えられます。
f(t) = \frac{1}{5}\mathrm{e}^{-t} - \frac{1}{5}\mathrm{e}^{-2t}\left(\cos{2t} - 2\sin{2t}\right)
(別解)複素数の極を個別に扱い、それぞれ部分分数分解する方法でも解を得ることができます。複素数の係数をA, D, E として次式のように部分分数分解を行います。
F(s) = \frac{A}{s+1} + \frac{D}{s+2-2\mathrm{j}} + \frac{E}{s+2+2\mathrm{j}}
A,D,E をそれぞれ計算します。
\begin{align*}
A &= (s+1)F(s)|_{s=-1} = \frac{1}{5} \\
D &= (s+2-2\mathrm{j})F(s)|_{s=-2+2\mathrm{j}} = -\frac{1+2\mathrm{j}}{10} \\
E &= (s+2+2\mathrm{j})F(s)|_{s=-2-2\mathrm{j}} = -\frac{1-2\mathrm{j}}{10}
\end{align*}
求めるラプラス逆変換 f(t) は次式で与えられます。
\begin{align*}
f(t) &= \frac{1}{5}\mathrm{e}^{-t} -\frac{1+2\mathrm{j}}{10}\mathrm{e}^{(-2+2\mathrm{j})t} -\frac{1-2\mathrm{j}}{10}\mathrm{e}^{(-2-2\mathrm{j})t} \\
&= \frac{1}{5}\mathrm{e}^{-t} - \frac{1}{5}\mathrm{e}^{-2t}\left(\cos{2t} - 2\sin{2t}\right)
\end{align*}
参考文献
- 荒木光彦(2000)「古典制御理論 基礎編」培風館 pp.22-25
Discussion