🤖
友達からボットを探す

2024/09/16に公開
GitHub
Netflix の番組[1]でベンフォードの法則を利用したボット判定について紹介されており、面白そうだったので出演者であるJennifer Golbeck の論文[2] を参考にして、実際に試してみました！

 ベンフォードの法則とはベンフォードの法則とは、自然に発生する数字の一桁目の頻度は均等ではなく、1から9まで数式に沿って減少するという法則です。


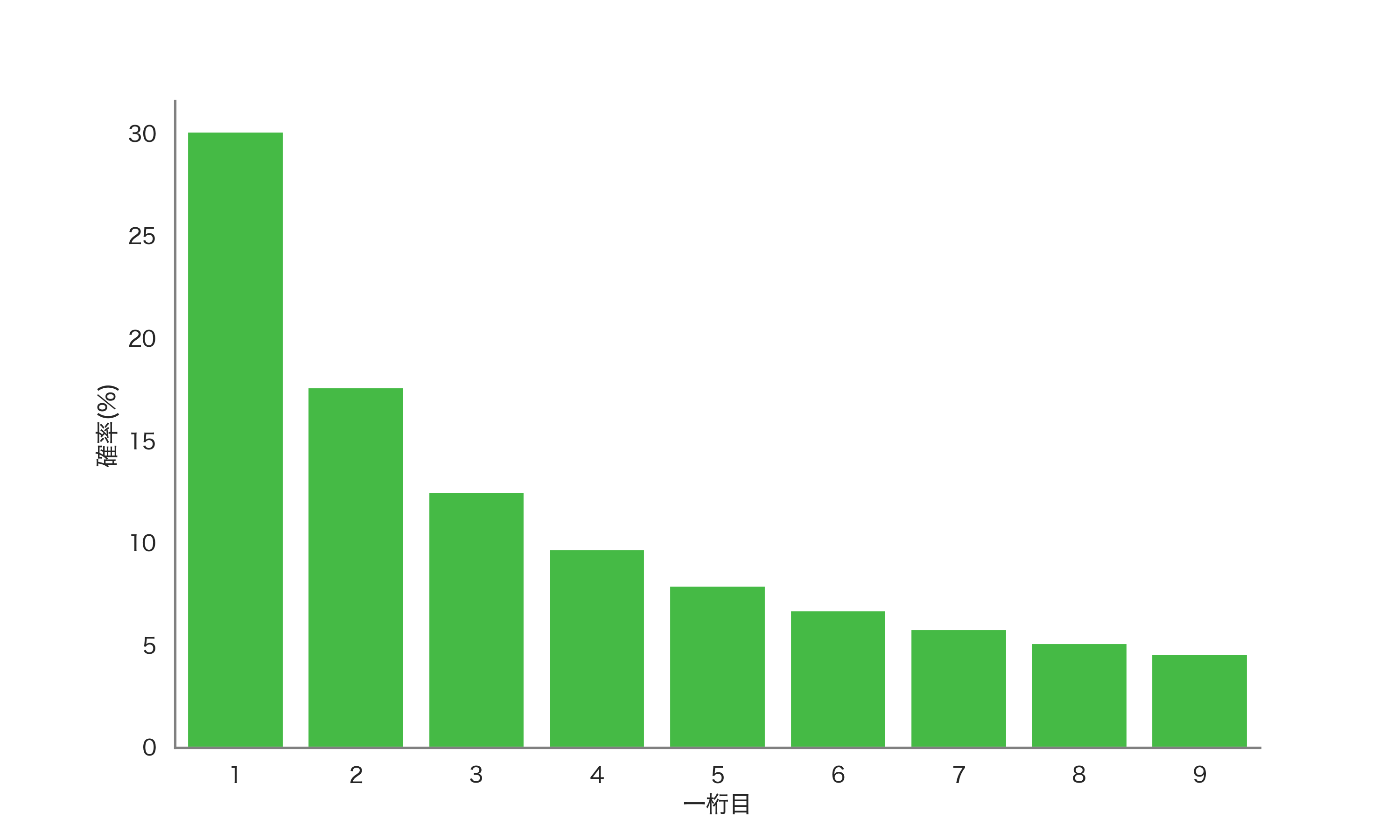
ご覧のように、最初の一桁目が"1"になるのは約30.1%、"2"になるのは約17.6%と減少していきます。
「自然発生する数字」が当てはまりやすいことから、人の手で操作された人為的な統計はこの確率分布から大きく外れる可能性が高いという点を利用します。
この法則は実は色々なところで活用されています。例えば、脱税の検出が有名な例です。納税者が提出する領収書に記載されている数字の最初の一桁目がこの分布から大きく外れていると、脱税の可能性が高くなることから活用されているだろうと言われています。

番組では脱税の検出以外にもこれから挙げるSNS のボット、ディープフェイクの検出などにもこの法則を使えることが紹介されていました。

 ボット判定への利用ベンフォードの法則について理解したところで、本題のSNS のボット判定にもこの法則が利用できることを見ていきましょう。

最初に挙げた論文によるとFacebook, Twitter, Google Plus、Pinterest、Live Journal の5つのプラットフォームの全てにおいてベンフォードの法則に沿うことが分かります。

※FSD とはFirst Significant Digits の略で1桁目を表しています。



from "Benford’s Law Applies To Online Social Networks"[2:1]

 試してみる実際にGitHub GraphQL API を使って、著名なアカウントのフォロワー・フレンド（フォローしてる人）がこの法則に従っているか検証します。データ取得に使用したコードをGitHub で公開しています。[3]
X ではやらないの？2024年9月現在のAPI 体系だとフォロワー・フレンドを取得するにはエンタープライズプランの権限が必要だったのでやめました🥺

 torvaldsLinux やGit を発明したリーナス・トーバルズさんのGitHub アカウントの、215,854人の全てのフォロワーのフォロワー数を取得し、一桁目をプロットしました。
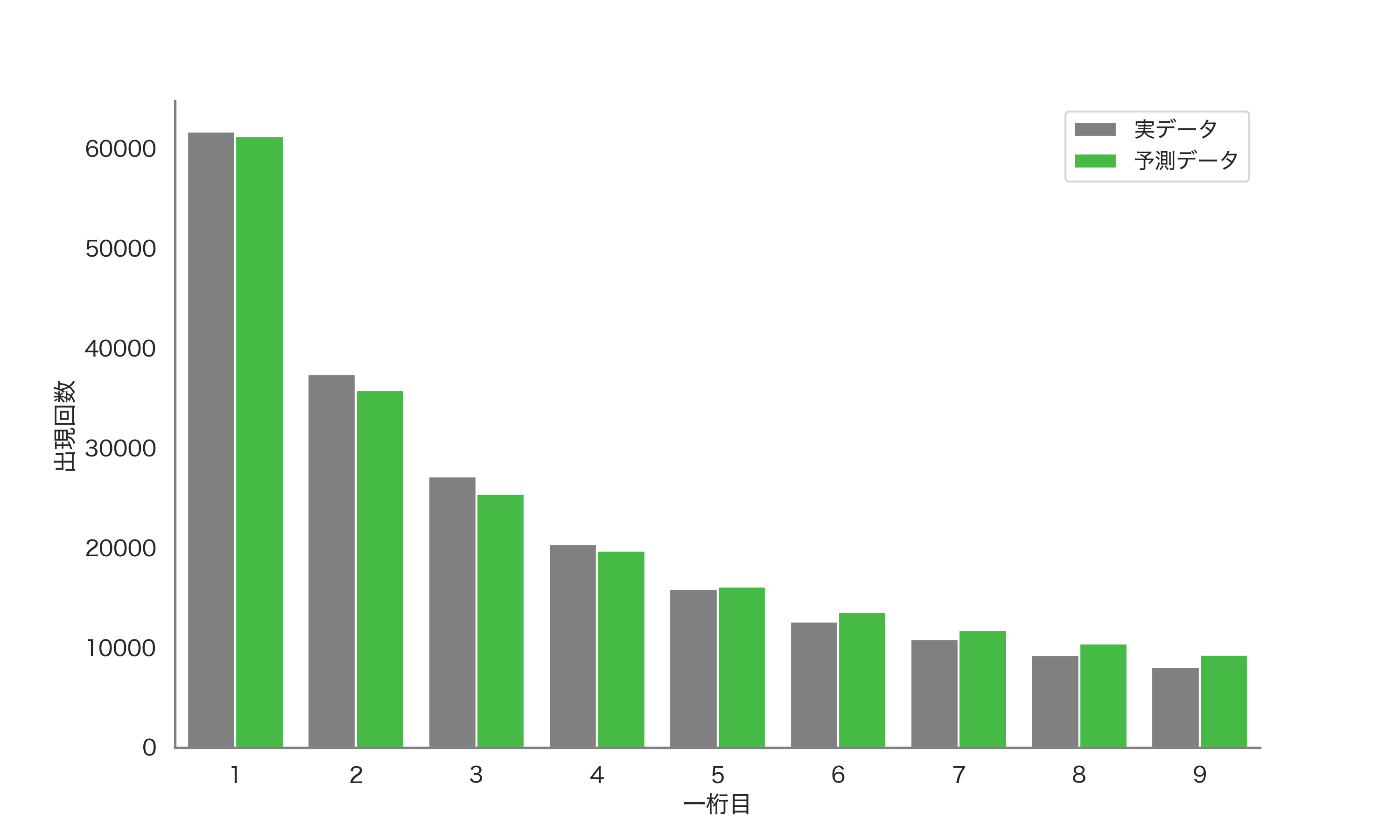
ベンフォードの法則での予測と実データに相関ありそうですね！

相関係数を計算すると、0.99855034という結果になりました。


from "Benford’s Law Applies To Online Social Networks"[2:2]
論文での計算結果と比較しても引けを取らない結果となりました。
次に、フォロワーのフレンド数を取得しプロットしました。

こちらも相関係数を計算すると、0.99996188というフォロワー数よりも高い相関が見られました。

 matzRuby を発明したまつもとゆきひろさんのGitHub アカウントの9,760人の全てのフォロワー・フレンド数の一桁目をプロットしました。


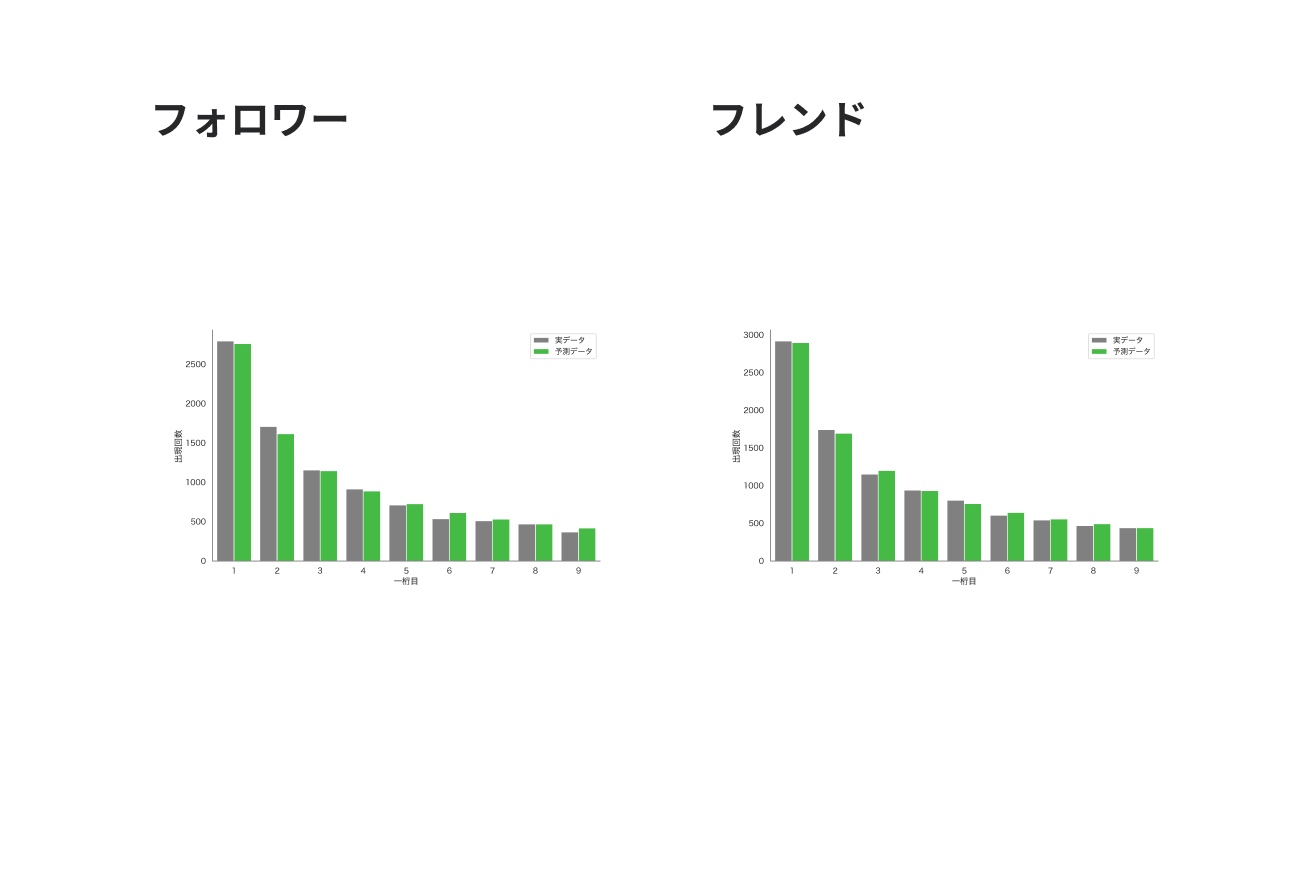
こちらも相関がありそれぞれフォロワー0.99873293、フレンド数0.99925624という高い相関係数が得られました。
ボットではないアカウントは法則に従うことがわかりました。

 数式で理解する自然発生する数字の一桁目に法則があるというのは、やはり不思議だと思います。ここで改めて法則を数式で理解してみましょう。
まずベンフォードの法則は、一桁目をdとして以下のような確率質量関数で表せます。

 P(d) = \log_{10}(1 + \frac{1}{d}) 
予測したい数字の一桁目が"2"ならば

    \begin{aligned}
        P(2) &= \log_{10}(1 + \frac{1}{2}) \\
             &= \log_{10}1.5 \\
             &\approx 0.176
    \end{aligned}
となります。
なぜ上記の確率質量関数で表せるのかを見ていきます。

ここまでの「自然に発生する数字」という表現を、指数関数的に増加するものと言い換えれます。感覚としても、フォロワーが1人から2人に増えるよりも8人から9人に増える方が早いというのがあると思います。
例えば、1日に2倍フォロワーが増えるとして数式で表します。

フォロワー数をx、増える時間をa とすると、

    \begin{aligned}
        x &= 2^a \\
        log_2{x} &= log_2{2^a} \\
        a &= log_2{x}
    \end{aligned}
フォロワーがx から1人増える時間をb とすると、

    \begin{aligned}
        x+1 &= 2^b \\
        log_2({x+1}) &= log_2{2^b} \\
        b &= log_2({x+1})
    \end{aligned}
これらを整理して、1人増える時間をb-a で表すと

    \begin{aligned}
        b-a &= log_2({x+1}) - log_2{x} \\
        &= log_2{\frac{x+1}{x}}
    \end{aligned}
桁が一桁(10人まで)の時間の中の1人増える時間の割合を求めます

    \begin{aligned}
        \frac{b-a}{log_2{10}} &= \frac{log_2{(\frac{x+1}{x})}}{log_2{10}} \\
        &= \frac{\frac{log_{10}\frac{x+1}{x}}{log_{10}2}}{\frac{log_{10}10}{log_{10}2}} \\
        &= log_{10}\frac{x+1}{x} \\
        &= \log_{10}(1 + \frac{1}{x})
        
    \end{aligned}
この割合が2桁以上になっても同じなので、そのまま最初の確率質量関数になります。

また、例としていた「1日に2倍」も「1日にn倍」でも同じ結果になります。

 まとめベンフォードの法則とは何か、2024年9月現在のGitHub でもその法則に従うこと、また数式からの視点でも学ぶことができました。

この記事でベンフォードの法則を活用する手助けになれば嬉しく思います。

また、論文を公開しているJennifer Golbeck、寛容にデータを取得可能にしているGitHub、わかりやすい数学の記事、動画を公開されている方々のおかげで、この記事を完成できました。この場で感謝申し上げます。

ご覧いただきありがとうございました👋

脚注
『ビックデータ黄金時代、世界の繋がりを科学する Ep:桁と数字の法則』https://www.netflix.com/jp/title/81031737?s=i&trkid=14170286&vlang=ja ↩︎
https://arxiv.org/abs/1504.04387 ↩︎ ↩︎ ↩︎
https://github.com/koshin01/research/tree/main/benford_laws ↩︎
ベンフォードの法則とは

ボット判定への利用

試してみる

torvalds

matz

数式で理解する

まとめ

Discussion
