音声の群遅延なんもわからん

これは日本音響学会 学生・若手フォーラム Advent Calendar 2023 の 11 日目の記事ですが、
群遅延だけに投稿日も遅延してしまいました、すみません......。

群遅延なんもわからん

群遅延 $\tau_{\rm{g}}$ は通常、以下のように位相 $\varphi(\omega)$ を角周波数 $\omega$ について微分し、マイナスをつけたものとして定義されます。

$$\tau_{\rm{g}}=-\frac{d\varphi(\omega)}{d\omega}$$

しかしこれを見ても、なぜ周波数について微分するのか？とか、このマイナスなんだよ！とか、直感的に分かりにくいです。
講義や教科書では詳しい説明は省かれることも多く、イマイチよく分かっていない方も多いのではないでしょうか？（私です）

しかしながら、比較的最近の研究 [1-3] でも度々取り扱われる重要な概念なので、知っておいて損はありません。
この記事では、群遅延の意味や興味深い性質について紹介していきます。

群遅延の直感的なイメージ

まず、時間 $t$ の信号 $x(t)$ の時間領域におけるエネルギー重心時刻 $\langle t \rangle$ を考えます。
簡単のため、エネルギーの総和が $1$ に正規化されているとすると $\langle t \rangle$ は

$$\begin{aligned} \langle t \rangle &= \int_{-\infty}^{\infty}t|x(t)|^2dt \end{aligned}$$

と書けます。
エネルギーで重み付けした時刻の平均ということで、$\langle t \rangle$ は 平均時刻（時間） と呼ばれます。

$\langle t \rangle$ は $x(t)$ の振幅スペクトル $A(\omega)$ と位相スペクトル $\varphi(\omega)$ を使って、

$$\begin{aligned} \langle t \rangle = \int_{-\infty}^{\infty}-\frac{d\varphi(\omega)}{d\omega} A^2(\omega)d\omega \end{aligned}$$

と変形することができます。

フーリエ変換のユニタリ性や振幅スペクトルの虚部が $0$ であることを利用しています。具体的な導出は森勢『音声分析合成』[4] やコーエン『時間-周波数解析』 [5] を参照してください。

ここで出てきた $-\frac{d\varphi(\omega)}{d\omega}$ は群遅延の定義そのものです。
平均時刻はパワースペクトル $A^2(\omega)$ によって重み付けされた群遅延に等しいことが分かりました。

パワースペクトルは周波数領域における信号のエネルギー分布ですから、各周波数のエネルギーで重み付けされた群遅延の和が平均時刻に相当することになります。つまり、信号の各周波数成分は群遅延分だけ遅れていると解釈できます。

音声信号における群遅延

群遅延とパワースペクトル

有声音信号のパワースペクトルには、基本周波数の整数次倍音からなる調波構造が現れることが知られています。では位相、群遅延はどうでしょうか？
以下は上からパワースペクトル、位相、群遅延をプロットしたものです。

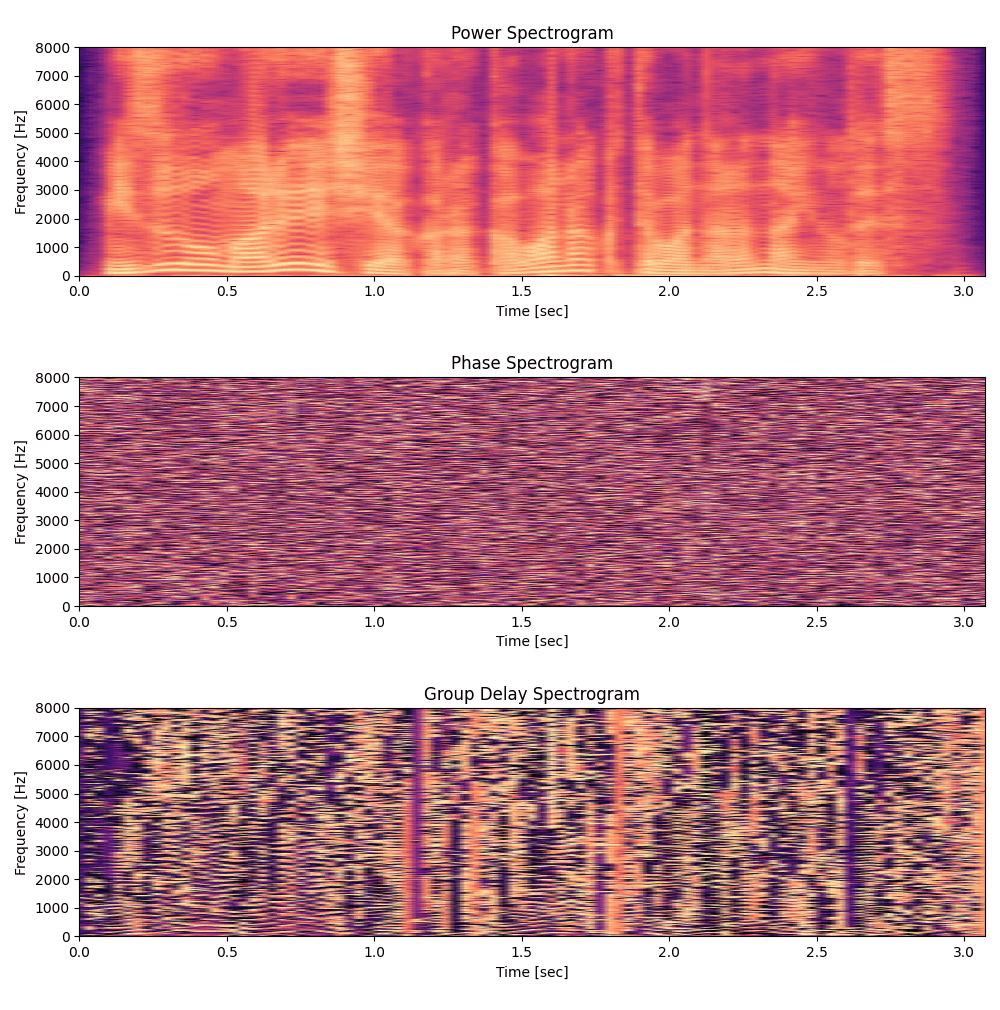
こうして並べてみると位相はランダムに見えるのに、群遅延には調波構造のような急峻なピークが観測されます。群遅延特性は各周波数成分の遅延のみならず、音声の何らかの性質を反映していそうです。

群遅延のピークは調波の谷で現れる

急峻なピークがパワースペクトルの調波に対応した形で現れるのはなぜでしょうか？
ここで、複素スペクトル $X(\omega)$ から群遅延を求めると関係性が見えてきます。

群遅延は位相とは異なり時間として求まるので、アンラップの問題を考える必要がありません。
しかし、位相に $0$ や $2\pi$ 付近の不連続なジャンプがある以上、微分を計算するためにはやはりアンラップを行う必要があります。
これを避ける方法として複素スペクトル $X(\omega)$ から計算できることが知られています。

$$\frac{-d\phi(\omega)}{d\omega} = \frac{\mathfrak{R}[\frac{dX(\omega)}{d\omega}]\mathfrak{I}[X(\omega)] - \mathfrak{R}[X(\omega)]\mathfrak{I}[\frac{dX(\omega)}{d\omega}]}{|X(\omega)|^2}$$

分母にパワースペクトル $|X(\omega)|^2=A^2(\omega)$ が現れました。これはパワースペクトルが小さくなるほどその周波数における群遅延の絶対値は大きくなることを示しています。
このことから、群遅延のピークはパワースペクトルが極小になる周波数成分、つまり調波の谷に現れると期待されます。

結局微分してるじゃないかと一見思いますが、フーリエ変換の微分公式 $\mathcal{F}[-itx(t)] = \frac{dX(\omega)}{d\omega}$ を使えば回避できます。

これも具体的な導出は省きます。詳しくは森勢『音声分析合成』[5]を以下略

群遅延包絡≒先鋭化されたフォルマント

先ほどは調波のような微細構造に着目しましたが、今度はフォルマントのような大局的なピークに注目してみましょう。
まず、スペクトルの共振成分を Linear predictive coding; LPC でモデル化します。
全極型フィルタの $p$ 個の極で表現しようとすると、それぞれの伝達関数 $H_i(z)$ は以下のようになります。

$$H(z)=\frac{1}{1+\sum_{i=1}^{p} \alpha_i z^{-i}}= \prod_{i=1}^{p} \frac{1}{1-z_i z^{-1}} = \prod_{i=1}^{p} H_i(z)$$

続いて、伝達関数のスペクトルのケプストラムを求めてみます。

これを信号から直接求めるケプストラムと区別して LPC ケプストラム と言います。

まず、対数を取って、

$$\log H_i(e^{j\omega})=\log A_i(\omega)+j\varphi_i(\omega)$$

次に、$\log A_i(\omega)$ と群遅延 ${\tau_{\rm g}}_i$ をフーリエ級数展開すると、

$$\begin{aligned} \log A_i(\omega)&=2 \sum_{n=1}^{\infty} \frac{{r_i}^n}{n} \cos n(\omega - \omega_i)\\ {\tau_{\rm g}}_i &= 2 \sum_{n=1}^{\infty} {r_i}^n \cos n(\omega - \omega_i) \end{aligned}$$

となり、級数の係数が LPC ケプストラムです。

導出は [Takamichi+ 2020] [2] や [Itakura+ 1987] [6] を参照してください。

群遅延は LPC ケプストラムの係数は $\frac{1}{n}$ 倍の関係にあることが分かりました。したがって $n$ が大きくなる、つまり高次になるほど群遅延の展開係数はケプストラムよりも大きくなるので、より鋭いスペクトルを成すことが期待されます。

合成音声の Buzzy 感との関連

ボコーダや旧来の TTS によって合成された音声はしばしば buzzy と形容されるブザーが鳴ったような音質劣化をともなうことがあります。これは基本周波数が低い音声において顕著です。
なぜこのような劣化が起こるのか完全には解明されてはいないものの、スペクトル包絡の過剰な平滑化や声道フィルタを駆動する音源の位相が原因ではないかと言われています。

位相も関係あるの？と思われるかもしれません。確かに人間の聴覚は基本的に位相の変化に鈍感ですが、150 Hz 以下の位相変化は音色に影響することが知られています [7]．
特に、チャネルボコーダの多くは駆動音源に周期インパルス列を利用しています。インパルスはゼロ位相のごく短い急峻な波形変化ですから、基本周期が長くなるとプツプツという音質が際立ちます。その buzzy 感が声道フィルタを畳み込んだ後も残ってしまうのです。

この buzzy 感の根本的な原因の一つとして、インパルスのように波形のエネルギーが時間的に局在していることが考えられそうです。
そこで、波形の持つエネルギーの散らばりとして、波形の平均時刻を中心としたエネルギー分散 ${\sigma_t}^2$ を以下のように定義します。

$$\begin{aligned} {\sigma_t}^2 &= \int_{-\infty}^{\infty}(t-\langle t \rangle)^2|x(t)|^2dt \end{aligned}$$

この $\sigma_t$ は信号のエネルギーが時間 $\left[\langle t \rangle - \sigma_t, \langle t \rangle + \sigma_t \right]$ において支配的に含まれることを意味するので、持続（継続）時間と呼ばれます。
また平均時刻と同様に、持続時間も位相スペクトル $\varphi (\omega)$ と振幅スペクトル $A(\omega)$ から以下のように計算できます。

$$\begin{aligned} {\sigma_t}^2 &=\int_{-\infty}^{\infty}{\left(\frac{d A(\omega)}{d \omega} \right)}^2 d\omega + \int_{-\infty}^{\infty}\left(\langle t \rangle - \tau_{\rm g}\right)^2A^2(\omega)d\omega \end{aligned}$$

森勢『音声分析合成』やコーエン『時間-周波数解析』を以下略

持続時間は振幅スペクトルと群遅延に依存することが分かります。
したがって、声質を変えずに buzzy 感を低減するには群遅延を制御すればよいことが示唆されます。

実際、SPIKES と呼ばれる手法は、平滑化した乱数に周波数に依存する重みを掛け、基本周期毎に群遅延の分布を設計し、インパルスの位相特性を操作することで buzzy 感を低減しています[8]。

加えて、最初の項は振幅スペクトルの微分が含まれています。振幅スペクトルが変化に乏しいほどこの積分は小さくなるので、スペクトル包絡が過剰に平滑化することで音質劣化が起こることにも説明がつきます。

おわりに

自身の理解が甘い部分が露呈し、執筆にかなりの時間を費やしてしまいましたがよい勉強になりました。この記事を読んだ皆さんの群遅延に対する理解が 1 マイクロ秒でも進めば幸いです。
もし間違いなどございましたら容赦なく突っ込んでいただけると助かります。

参考文献

[1] Y. Masuyama, et al., “Phase Reconstruction Based On Recurrent Phase Unwrapping With Deep Neural Networks,” in Proc. ICASSP, 2020, pp. 826-–830.
[2] S. Takamichi, et al., “Phase reconstruction from amplitude spectrograms based on directional-statistics deep neural networks,” Signal Processing, vol. 169, p. 107368, 2020.
[3] Y. Ai, et al., “APNet: An All-Frame-Level Neural Vocoder Incorporating Direct Prediction of Amplitude and Phase Spectra,” IEEE/ACM TASLP, vol. 31, pp. 2145-–2157, 2023.
[4] 森勢 将雅, “音声分析合成,” コロナ社, 2018.
[5] L. コーエン, “時間-周波数解析,” 1998.
[6] F. Itakura, et el., “Distance measure for speech recognition based on the smoothed group delay spectrum,” in Proc. ICASSP, IEEE, pp. 1257-–1260, 1987.
[7] R. Plomp, et al., “Effect of phase on the timbre of complex tones,” Journal of ASA., Vol. 46, No. 2B, pp. 409-–421, 1969.
[8] 河原 他, “オールパスフィルタの位相操作による時間構造制御とその知覚への影響について,” 聴覚研究会資料, 1996.