🍭

2023年の Linear Haskell で純粋・並列 FFT を実装する──「Haskell は Rust になれるのか？」補遺

2023/12/14に公開

Haskell

この記事は Haskell Advent Calendar 2023 14 日目の記事です^[1]。

更新履歴

2023-12-15 並列化のパフォーマンスに関する追記。
2023-12-14 初版公開。

はじめに

先々月、Linear Haskell のまとまりのない記事を書いたところ、思ったよりも反響を頂いてびっくりしました。

ただかなりまとまりのない長文だった結果、「長い」「結局 Rust になれるのかようわからん」といった御叱りを頂きました。本当にすいません……。
冒頭に「RustのようになるにはLinear Constraintsに期待」とか、末尾に「2023年のHaskellはまだ Rust ではないが、近い将来 Rust になれる可能性が大きい」とか書きはしましたが、全体があまりにも長いのでこの結論を見つけ出すのも大変ですし、話題があんまり散漫に過ぎまたので論拠もすごくわかりづらかったなと反省しきりです。
そこで、本記事では 「Rust になれそうな Haskell」というのが現状どんなもの で、将来的にどこまで近づき得るのか、ということを例を使って示してみたいと思います。

本記事の目標は以下の通りです：

2023年現在の Linear Haskell での純粋な可変配列の扱い雰囲気を把む
Rust 的な所有権が Linear Haskell でどう定式化されるのかを把握する
RankNTypes と Token によるスライスの扱いの雰囲気を学ぶ
Linear Constraints が入った未来の Linear Haskell の姿を幻視する

細かい説明は上記記事にあったりしますが、いかんせん詰め込みすぎてわかりづらいので、軽く読む上では本記事だけで雰囲気を掴めるようにはつとめたつもりです。
本記事の内容は、Linear Constraints の応用例のうち、可変配列に関するところだけを採り上げて集中的に説明したものです。
Linear Constraints はかなり Linear Haskell に革命を齎すもので、GHC Proposal が出されているところです。是非みなさん 👍❤️🚀 しましょう。

具体的には、高速Fourier展開を題材に、まず旧来の Haskell での ST-モナドを使った実装を復習したあと、それが 2023 年の Linear Haskell でどのように純粋に書き直せるかを確認します。Linear Haskell で純粋化したお陰で、GHC の軽量並列計算のプリミティヴを使って手軽に FFT の分割統治法を並列化できるようになります。更に、トークンを使った定式化によりリソースそのものと所有権を切り離し、細かく制御できるようになることを示します。
2023年のLinear Haskellではまだトークンを引き回す必要があり煩雑ですが、最後に上述の Linear Constraints によりトークンを暗黙的に扱えるようになり、書き心地が飛躍的に向上し Rust みたいになるという未来を幻視します。お楽しみに！

それでは、本編をどうぞ。

題材：並列・純粋・In-place 高速 Fourier 変換

この記事では、(Cooley-Tukey の)高速Fourier（フーリエ）変換を題材に取るので、簡単にどういう問題なのか説明しておきます。
手短かにいうと、Fourier変換というのは入力された波形から、周波数成分を高速に抽出するアルゴリズムです。
形式的には、Fourier 変換は関数 $h: ℝ \to ℂ$ が与えられたとき、以下を満たす関数 $H: ℝ \to ℂ$ を求めよ、という問題です：

h(t) = ∫_{-∞}^∞ H(f)e^{2πi ft} \mathrm{d} f

積分が出て来るとこわく感じるひとがいるかもしれませんね。計算機で解くのはこれを離散化した離散Fourier変換問題なので、もうちょっとこわくない表示になります。
具体的には、離散Fourier変換は以下のような問題です：

$N \in ℕ, Δt \in ℝ$ とし、 $f_k = \frac{k}{NΔt}$ として、関数 $h: ℝ \to ℂ$ が次のように表されるとします：

$h(t) = \sum_{k = -N/2}^{N/2} H_k \left[\cos(2πf_k t) + i\sin(2πf_k t) \right]$
各 $h_k = h(k Δt) \; (k = 0, \ldots, N - 1)$ の値を教えてあげるので、お礼に各 $H_k\; \left(-\frac{N}{2} ≤ k ≤ \frac{N}{2}\right)$ の値を教えてください。

これがわかると波形の処理ができたり、統計が出せたり、うれしいことがいっぱいあります。うれしいですね。

ふつうの Haskell によるCooley–Tukey 法による高速Fourier変換

離散 Fourier 変換は $N = 2^n$ の形のとき高速に^[3]解けることが知られており、ここでは一番有名な解法である Cooley–Tukey 法を扱います^[4]。

Cooley–Tukey 法は典型的な分割統治法アルゴリズムで、本記事を理解するには概ね次のような流れで計算が進むことだけ理解していれば十分です：

前処理として、入力を添え字のビット列が逆になるように並び換える（ビット反転）。
長さが1ならなにもしないで終わり。
長さが2以上の場合：
a. 左半分と右半分にわけて、それぞれ独立に (2) (3) を適用
b. 終わったら適当な係数をかけたり足したりするバタフライ演算を、左右あわせた配列全体に適用
できあがり！

(2)(3)が分割統治法の心臓部ですね。前処理後、半分にしながら再帰していって、一段終わるごとに後処理をして戻る、ということだけ覚えておけば大丈夫です。

この記事で大事なこのアルゴリズムの特徴は、以下の二点です：

入力の配列を使い回せるので、破壊的変更を使えば余計な配列のアロケーションが必要ない（In-place である^[5]）^[6]
分割統治法なので、二分割した再帰のフェーズはそれぞれ並列にできる

ネタバレをすると、破壊的変更を純粋にやることと、二分割したスライスを安全に他スレッドに貸し出すことに Linear Type を使い、更に貸し出し部分については将来的に入る Linear Constraints で著しく簡単になります。

それでは、一旦ふつうの Haskell ^[7] での実装例として、STモナドと可変配列を使った実装を見てみましょう。

import Data.Complex
import qualified Data.Vector.Unboxed as V
import qualified Data.Vector.Unboxed.Mutable as MV

fft :: V.Vector (Complex Double) -> V.Vector (Complex Double)
fft = V.modify fftM

fftM :: MV.MVector s (Complex Double) -> ST s ()
fftM v0 = do
  bitReverse v0
  let !n = V.length v0
      !theta = 2 * pi / fromIntegral n
  loop v0 n (cos theta) (sin theta) 
  where
    loop v !n !c !s
      | MV.length v == 1 = pure ()
      | otherwise = do
          let !half = n `quot` 2
              !dblCs = 2 * c * c - 1
              !dblsn = 2 * s * c
              !kW = c :+ s
              (lh, rh) = MV.splitAt half v
          loop lh half dblCs dblSn  -- (*)
          loop rh half dblCs dblSn  -- (*)
          forM_ [0..half - 1] $ \k -> do
            ek <- SV.read arr k
            ok <- SV.read arr $ half + k
            SV.write arr k (ek + kW ^ k * ok)
            SV.write arr (half + k) (ek + kW ^ (half + k) * ok)


bitReverse :: MV.MVector s a -> ST s ()
bitReverse = {- 省略 -}

ごく普通ですね。fft では不変配列を受け取って、そのFFT結果を返します。これは modify 関数を使って一旦不変配列を適宜コピーした可変配列を作成し、実際のアルゴリズムである fftM に渡しています。
fftM が可変配列に対して実装された実際のアルゴリズムで、破壊的変更を使って実際の処理を行っています。
bitReverse 関数は前処理のビット反転を行う関数ですが、今回は主題ではないので実装は省略しています。

さて、ここで ST モナドがどのようにして局所的な可変状態を総体として純粋に扱えるようにしているのか復習しておきましょう。
modify の型は次の通りでした：

modify :: (forall s. MVector s a -> ST s ()) -> Vector a -> Vector a

ST モナドが局所的な可変状態を純粋に扱えるのは、この第1引数の関数で s が全称量化されているのがミソなのでした。
modify ですと恩恵がわかりづらいですが、本質的に modify が使っている次の runST を考えてみます：

runST :: (forall s. ST s a) -> a

ここでも、s が全称量化されています。ポイントは、sが束縛されているのは第1引数の中のみで、返値ではないという点です。
s は forall で括られているので、どんな変数を代入しても結果は変わらないことが要請されます。特に、返値の a はスコープの外に出ていますから、 a の具体的な型には変数 s はが現れることができません。なので、特に可変配列である MVector s b のような型は、runSTの外に抜け出すことはできません。
このように、「リソースがスコープ外に漏れ出ることがない証拠となる変数」の役割を果たす束縛変数を、Skolem変数と呼びます^[8]。
このトリックは、Linear Haskell でスライスを扱う際にも出てきます。覚えておきましょう。

STモナドを使った解決策もまあまあ良い感じですが、いくつか問題点があります。

モナドを使っている：もちろん、モナドを使うことは悪ではなく、むしろ副作用が型レベルで区別されるという Haskell 最大の美点の一つです。しかし、ここでの副作用＝破壊的操作の効果は局所的であり、純粋に書けるのであればそれに越したことはありません。
並列化ができない：コメント (*) 部分の lh と rh に対する loop の呼び出しは本来並列化できます。
しかし、STモナドは並列化用の演算子を標準では提供していないため、逐次実行になっています。
単純に par 呼んでやったらどう？と思うかもしれませんが、これは純粋な式が対象のものなので、第1引数の値を捨ててしまい、第2引数のものしか評価されないので上手くいきません。
これは、ST モナドの内部では資源の区別ができないため、並列演算子を定義すると実行順序の非決定性により純粋性が破れる可能性を型安全に排除できないからです。

それでは、2023 年の Linear Haskell を使ってこれらがどう解決され、未来の Linear Haskell でどう改善されるのかを見ていきましょう。

2023 年の Linear Haskell による並列・純粋・In-place Cooley–Tukey法

Linear Haskell の復習

実際の解法にうつる前に、最初に Linear Haskell のあらましを駆け足で思い出してみましょう。もうちょっと細かい事を知りたい場合は親記事の節「魔法の箱 Ur と線型性の呪い」以下数節を、後で読んでみてください。

LinearTypes 言語拡張を有効化した Haskell では、あたらしい関数型構築子 %1 -> が導入されます。f :: a %1 -> b という型を持つ関数 f があったとき、項 f x の型検査・推論時には次のような制約が満たされているかどうかが静的に検査されるのでした：

式 f x を「ちょうど一回だけ消費」された時、 x も「ちょうど一回だけ消費」される。

「ちょうど一回だけ消費」の定義は前の記事や論文に譲りますが、おおまかにいえば、プリミティヴな値は完全に評価され、代数的データ型についてはコンストラクタに対するパタンマッチが行われてその「線型なフィールド」が「ちょうど一回だけ消費」されればよい、と理解すればよいです。

これを Rust 的な所有権の言葉でふわっと言い換えてみれば、線型関数 f :: a %1-> b は「f 内の処理では、完全に a の値が消費されるまでの将来にわたって、a の所有権を持っている者はちょうど一人しかいない」事が静的に保証された関数と見ることができます。

代数的データ型の消費について補足すると、LinearTypes が有効化されていようがいまいが、代数的データ型の通常のフィールドは線型フィールドとして解釈されます。
非線型（無制限）なフィールドを宣言するには、GADTs または GADTSytnax を陽に宣言します。例を見ましょう：

data MyData where
  MkMyData :: Int -> Bool %1-> Char -> MyData

ここで、MkMyData のフィールドのうち、 Int 型と Char は非線型な（何回でも使える）フィールドであり、Bool 型のものは線型なフィールドとして宣言されます。
このようになっているのは、タプルや Maybe, Either など、既存の型の線型版をいちいち再定義しなくてすむようにするためです。
例としては、Just :: a %1-> Maybe a, (,) :: a %1 -> b %1 -> (a, b) のような型がつきます。特に、タプルは計算結果と線型な値を返すのによく使われるので重要です。
デフォルトで線型な型しか仕舞えないのであればそれはそれで不便では？と思うかもしれませんが、このGADT構文を使って値を無制限に保持するためのデータ型として Ur a という型が用意されていました：

data Ur a where Ur :: a -> Ur a

この唯一のフィールドは非線型なので、Ur に対するパターンマッチさえちゃんとすれば、取り出した値は何回でも使うことができます。
逆に、Ur がフィールドについて非線型になっているので、線型に束縛された値を Ur に包むことは直接的にはできなくなっています。

また、2023年時点の GHC （9.8 系まで）では、線型束縛用の let-式がサポートされていないのでした。なので、線型資源を局所的に束縛するには、後置関数適用演算子 (&) の線型版を使う必要があるのでした（linear-base の Prelude.Linear モジュールで提供されています）：

(&) :: a %1-> (a %1 -> b) %1 -> b

たとえば、以下のような人工的な例を考えます：

useA :: a %1 -> b
useB :: b %1 -> c

f :: a %1 -> ()
f a =
  let b = useA a
      c = useB b
   in consume c

これは、GHC 9.8 時点では以下のように書く必要があります：

f :: a %1 -> ()
f a = useA a & \b -> useB b & \c -> consume c

これはちょっと不便なので、線型な let を実装しましょう、という GHC Proposal が出されています：

上記の Proposal が入ると、次のようにちょっとしたアノテーションをすれば let-式で書けるようになります：

f :: a %1 -> ()
f a =
  let %1 b = useA a
      %1 c = useB b
   in consume c

実装担当者を探しているようなので、気が向いた人は名乗りを挙げるといいんじゃないでしょうか。

2023 年の Linear Haskell の解法

さて、それでは前節の問題を2023年現在の Linear Haskell でどう解決するか考えましょう。具体的には、心臓部である loop 部分の書き換えを考えてみます。

(1) の脱モナド化については、既に Linear Haskell の原著者の人々が開発しているライブラリ linear-base には配列に対する破壊的変更を純粋に行うためのAPIが提供されています：

関係がありそうなの API はこちらでしょう：

fromList :: [a] -> (Array a %1 -> Ur b) %1 -> Ur b
set :: Int -> a -> Array a %1 -> Array a
get :: Array a %1 -> (Ur a, Array a)
slice :: Int -> Int -> Array a %1 -> (Array a, Array a)

ここで、slice は元の配列とその与えられたオフセットと長さを持つ部分列の複製を返すものです。

これを使えば (1) はクリアできそうです。何せ純粋ですから。
では (2) の並列化についてはどうか……というと幾つか問題があります。
仮に slice で前半・後半の部分列をつくったとしましょう^[9]。これらに対しては上の純粋なインタフェースが使えるので、標準の純粋な par を使って再帰ができそうです。
しかし、標準の par は非線型な型を持つので、slice の結果をそのまま渡すことはできなません：

par :: a -> b -> b -- ^ 引数の矢印が非線型！

では、これを線型にするとどうでしょうか？例えば……

par :: a %1 -> b %1 -> b

としたらどうでしょうか？概ねよさそうです。但し、これでは折角並列に評価した a の値が捨て去られることになってしまいます。
なので、次のような型を持つ線型な par があればよさそうです：

par :: a %1 -> b %1 -> (a, b)

ふむふむ、良さそうです。では slice を使って前後二つのスライスを作り、par を使えばいいか──というとそうは問屋が卸しません。なぜか。上でしれっと書いたように、slice 関数は部分列の複製を返すという点が問題になります。FFTは In-Place に配列を変更することで空間・時間効率を達成しています。なので、部分列を複製する slice を使うと、データを複製する操作に加え、分割統治して返ってきた配列の値を元の配列に書き戻す手間が発生してしまい、効率が悪化してしまいます。

そもそも、なぜ slice は複製を返すのでしょうか？
それを理解するために、線型型でどうして配列への破壊的変更を純粋化できるのかについて考えてみましょう。
線型に束縛された資源は、最終的に「ちょうど一回だけ消費」される必要があるのでした。この性質によって、線型束縛された配列 arr :: Array a は消費されきるまでちょうど一人だけがその所有権を持っていることが保証できます。これによって同時アクセスの可能性を排除できるので、直列実行であれば結果は常に決定的となり純粋に扱えるという寸法です。また、parも上のように各引数について線型に束縛するようにすれば、線型束縛された資源に触れるスレッド（というかスパーク）も一つしかないことが保証できます。
見方を変えれば、上の API は可変配列をその所有権ごと set や get などの関数に貸与している（set や get が借用している）と見ることができます。これらに所有権を貸与して値を変更したり読み出したりしたりした後、も freeze や free などで消費するまでは引き続き処理をしたい訳ですから、set や get は渡された元の配列が返却されるのも大事です。

これを念頭におけば、slice が複製を行う必要性がわかるでしょう。たとえば、slice で元の配列 xs といっしょに真ん中の列 ys を取り出したとします。

 |<--- xs ---->|
 |             |
 0  1  2   3 4 5
    |      |
    |<-ys->|

すると、xs と ys は別々に変換できますが、それぞれ 1〜3の部分を同時に触ることができてしまいます。すると、遅延評価や並列性の存在下では、評価タイミングによって値が非決定的になってしまう可能性があります。
これを回避するため、上のAPI では slice が複製を返すようになっていたわけです。

ところで、今回必要なのは任意の場所からのスライスではなく、真ん中から二つに割ることができればよいのでした。
分割された二つの配列に重なる部分はありませんし、それなら元の配列を忘れて「半分にした左右半分をそれぞれ返す」次のような関数があればどうでしょう？

halve :: Array a %1 -> (Array a, Array a) -- ^ 左半分と右半分に分けてかえす

これなら、次のようにして loop 関数の半分まではうまく実装できそうです：

{-# OPTIONS_GHC -Wno-name-shadowing #-}

loop :: Array (Complex Double) %1 -> Int -> Double -> Double -> ()
loop arr !n !c !s =
if n <= 1
  then rw
  else
   let !half = n `quot` 2
       !dblCs = 2 * c * c - 1
       !dblSn = 2 * s * c
       !kW = c :+ s
    in halve arr
        & \(lh, rh) -> 
            loop lh half dblCs dblSn
              `par`
            loop rh half dblCs dblSn
        & \(lh, rh) -> ???

上の par を使って lh, rh を別々のスレッドに貸し出して再帰的に計算し、その結果を返却してもらって続きの計算をしようという訳です。
問題は、??? の部分──返ってきた lh と rh から arr を復元できるか？という点です。
もとの配列は split に渡して使えなくなっているので、分割後の配列から元のものを復元する手段が必要になります。次のような関数 combine が欲しいような気がしますが……

combine :: Array a %1 -> Array a %1 -> Array a

……が、しかし、これは二つの引数の間に何の制約もありません。別々に allocate された二つの配列が渡されたらどうすればいいんでしょう？実行時エラーにするしかない気がしますが、それでは型安全性が終わってしまいます。Maybe (Array a) を返すようにしてもいいかもしれませんが、折角なら適切な配列の対に対してしか combine を呼べないようにしたいところです。我々は強い型の世界にいるので……。

それには、型レベルで異なる配列を区別できるといいんですが──というところで、ハイ、そうです。Skolem変数の出番です。
Array の最後に一個 Skolem 変数を入れる型パラメータを足してしまいましょう：

data Array a n
fromList :: [a] -> (forall n. Array a n %1 -> Ur b) %1 -> Ur b
set :: Int -> a -> Array a n %1 -> Array a n
get :: Array a n %1 -> (Ur a, Array a n)

では、halve はどのような型をつければいいでしょうか？分離された左右のスライスは、元の配列から区別される必要があり、同時に二つの配列から元の配列を復元できる「証拠」が必要です。
そこで、「配列 l, r はもともと一つの配列 n を適当なところで分割した対である」ことを表す型 Slices n l r を導入し、更に存在型を使って l, r を存在量化することで、都合三種類の配列の間の区別を付けることにしましょう。
結果的に得られる API は次のような感じになります：

data SlicesTo n l r
data Slice a n where
  MkSlice :: SlicesTo n l r %1-> Array a l %1 -> Array a r %1 -> Slice a n

halve :: Array a n %1-> Slice a n
combine :: SlicesTo n l r %1 -> Array a l %1 -> Array a r %1 -> Array a n

Slice は GADT として宣言されており、 l, r が存在型変数として隠蔽されていることに注意しましょう。
Slice は l, r が n の分割であることの証拠となるトークンと呼ばれるものです。

これを使えば、次のように書き換えることができます：

loop :: Array (Complex Double) n %1 -> Int -> Double -> Double -> ()
loop arr !n !c !s =
  {- ... -}
  let !half = n `quot` 2
      !dblCs = 2 * c * c - 1
      !dblSn = 2 * s * c
      !kW = c :+ s
   in halve arr 
      & \(MkSlice slices lh rh) -> 
        loop lh half dblCs dblSn
          `par`
        loop rh half dblCs dblSn
      & \(lh, rh) -> 
        combine slices lh rh & \arr ->
        forN half
          (\k ->
            get k arr                 & \(Ur ek, arr) ->
            get (half + k) arr        & \(Ur ok, arr) ->
            set k (ek + kW ^ k * ok)  & \arr ->
            set (half + k) (ek + kW ^ (half + k) * ok)
          )
          arr

-- | @n@ 回繰り返す
forN :: Int -> (Int -> a %1 -> a) -> a %1 -> a
forN n f = go 0
  where
    go :: Int -> a %1 -> a
    go !i x
      | i >= n = x
      | otherwise = go (i + 1) (f i x)

これで一応は動く例ができました！無事純粋・並列・In-Place な FFT が実装できたわけです！やったー！

……しかし、毎回同じ配列を渡しては受け取って……と引き回しているのがちょっとやですね。ST-モナドを使った例では、arr や lh, rh は最初に一回束縛したら計算の結果（ek, ok など）を受け取って、同じ配列を別々の関数に渡すだけで済んでいました。
なぜでしょうか？Linear Haskell では、操作関数に所有権を排他的に貸し出す（あるいは関数が配列の所有権を借用する）ようにすることで、可変配列の純粋性を保証しているのでした。
それなら、上で「スライスである」ことのトークンを用意したように、「配列の読み書きの所有権」を別のトークンとして切り出してみたらどうでしょう？
その上で、配列そのもの自体は非線型な束縛を前提として、所有権トークンだけ線型に束縛するようにしたらどうでしょうか？
以下のように、「n の配列から読み込める」所有権 R n、「n に書き込める」所有権 W n、それらを組にした RW n を定義して、それを使って値を操作するように、API を書き換えてみましょう：

data RW n = RW (R n) (W n)
data R n
data W n

fromList :: [a] -> (forall n. RW n %1 -> Array a n -> Ur b) %1 -> Ur b
get :: R n  %1 -> Array a n -> (Ur a, R n)
set :: RW n %1 -> Int -> a -> Array a n -> RW n

data SlicesTo n l r
data Slice a n where
  MkSlice :: 
    SlicesTo n l r %1-> 
    RW l %1 -> RW r %1 -> 
    Array a l -> Array a r -> Slice a n

halve :: Array a n %1-> Slice a n
combine :: 
  SlicesTo n l r %1 ->
  RW l %1 -> RW r %1 -> 
  Array a l -> Array a r -> 
  (Array a n, RW n)

fromList が新たに RW n を線型に渡すようになっていること、各関数に現れる Array a n たちが非線型束縛になっていることに注意しましょう。

これを使えば、loop は次のように書き換えられます：

loop :: RW n %1 -> Array (Complex Double) n -> Int -> Double -> Double -> RW n
loop rw arr !n !c !s
  {- ... -}
  let !half = n `quot` 2
      !dblCs = 2 * c * c - 1
      !dblSn = 2 * s * c
      !kW = c :+ s
   in halve rw arr 
        & \(MkSlice sliced rwL rwR lh rh) ->
            loop rwL lh half dblCs dblSn
              `par` 
            loop rwR rh half dblCs dblSn
        & \(rwL, rwR) ->
          combine sliced rwL rwR lh rh & \(Ur arr, rw) ->
            forN half
              ( \ !k (RW r w) ->
                  get r k arr & \(Ur ek, r) ->
                  get r (half + k) arr & \(Ur ok, r) ->
                  set (RW r w) k (ek + kW ^ k * ok) arr & \rw ->
                  set rw (half + k) (ek + kW ^ (half + k) * ok) arr
              )
              rw

配列を引き回す必要性が消えましたね！
ちょうど、Rust の型修飾子で &'n mut とか &'n とか書くかわりに、ここでは RW n や R n といったトークンを引数として渡している訳です。

……でも、結局 RW とか R とか W とかのトークンを引き回すことになってしまいました。
それでも、書き込みと読み出しを別々の所有権として分離して、所有権貸与の粒度を高めることができました。今回の FFT の例では R だけを使うような大きな処理はありませんが、大規模なプログラムを書く上では、書き出しだけを要求する巨大な関数などもあり得ますし、確実に表現力は上がっています。
また、グラフなどコンテナの中に同じ配列への参照を複数保存しておきつつ、所有権は排他的に管理することもできるようになります^[10]。

そしてこれはネタバレなんですが、Linear Constraints が GHC に実装されれば、これら RW, R, W, そして SlicesTo などのトークンは人間が書かずにコンパイラが自動的に推論してくれるようになります！詳細は後ほど。

本節で実装した FFT の完全なソースコードは以下にあります。

ちゃんと動くでしょうか？
以下は、関数 $F(t) = \sin(2πt) + 2 \sin(πt) + 3 \sin\left(\frac{1}{2}πx\right)$ をためしに展開してみたときの周波数表示です：

いいかんじの周波数成分が出ていますね

いいかんじです！本当に並列化できているのかって？上の結果を4並列で計算させてみた時の各スレッドの使用率を ThreadScope で可視化したものが次になります：

四つとも綺麗に使われている

ちゃんと4つとも均等に使われています。やりました！

並列化がちゃんとできているか、物凄く疑り深い人のための補足

「これだけだと本当にちゃんと並列化できてるのかわからん」というお叱りを受けました。そもそもこの記事の趣旨は「FFTを題材に現在と未来の Linear Haskell の雰囲気をつかむ」ことであって、「Linear Haskell で爆速の FFT が実装できる」とは1ナノメートルも書いていない（そもそも、爆速並列FFTを実装したいのなら Couley–Tukey の自明な並列化を選んだだけで満足する訳がない）ので、上の「4並列でスレッドがちゃんとutiliseできている」ThreadScopeの絵で十分だろうと判断しました（し、この判断は妥当だと思っています）。

それでも、やっぱりどれくらい並列化できているのかというのは気になるところだと思います。
結論を先に言うと、並列化は一定程度出来ているが、雑な実装なのでぜんぜんスケールしないというところです（それはそう）。
爆速FFTの実装は本記事の目的ではないので詳細を長々と書いても仕方ありませんから、詳細は以下の「詳細」のところに書いておきます。興味のある人だけ読んでください。

詳細

ベンチマークに使ったコードは次です：

ベンチマーク環境は以下の通り：

MacBook Pro 15-inch 2019
Intel Core i7 2.6GHz 6コア（仮想12コア）
32GB RAM搭載
GHC 9.0.2 で -O2 をつけ、nonmoving GC 有効化。

そんなにコア数がないので、雑に概算して概算 $8192$ 要素 × ワーカスレッド $256$ 個＝ $2,097,152$ 要素くらいまで調べています。そんなに大きくはないですが、別に大規模FFTができるとは1ピコメートルも主張していないので、まあこんなもんでいいでしょう。

総要素数を $2^21 = 2,097,152$ とし、並列数を $1, 2, 4, \ldots, 256$ と変化させたものです。縦軸は、シングルスレッドの時の所用時間を $1.0$ として何倍高速化されたかです。

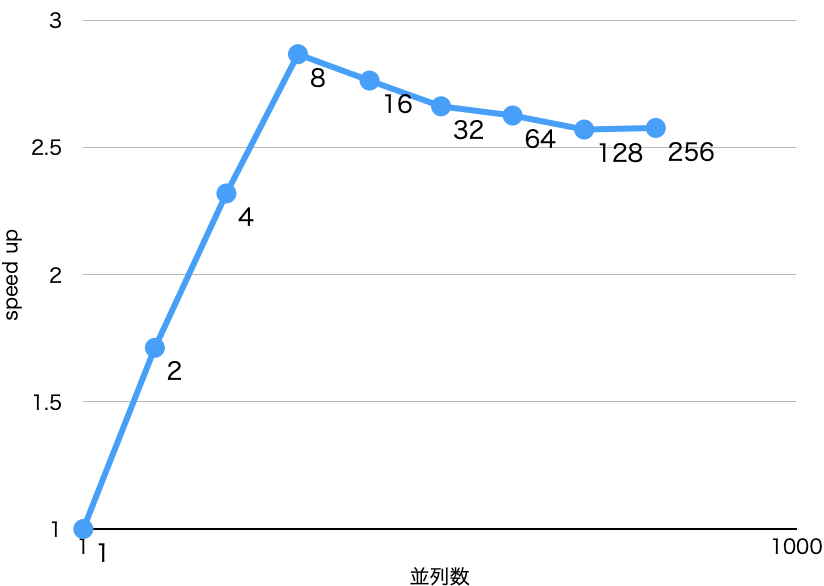
Strong Scale 線型っぽい

並列数が $8$ くらいまではスケールしていますが、16から落ちて段々頭打ちになっています。使っているマシンが実6コア、仮想12コアしかないのもありますし、非常に微妙とはいえ、並列化の効果はかすかに出ていると言えそうです。

では今度は弱スケーリングを見てみます。スレッド当りの要素数がだいたい 8192くらいになるように狙って、並列数を同様に変化させたものです。ちゃんと弱スケールしているなら傾きはゼロに近付いてほしいところですが……

弱スケールしていない

まったく弱スケールしてないっすね！
ベンチマークのコードではスレッド数 $N$ を都度セットしつつ、直列計算する閾値を $8192$ として、要素数は $8192 \times N$ にすることで大雑把にスレッド当りのデータサイズを固定しようとしています。しかし、今回の実装は再帰するときに雑に par で spark を作ることを繰り返していて、いわばトップダウンの雑な並列化といえます。なので、作られるスパークの個数は使えるスレッドの個数よりも多く（スパークは軽量なので問題はない）、実際にスレッドがスパークをどう実行するかは完全に GHC に任せています。GHCのスケジューラはあるていど賢いので、なるべくスレッドが均等にスパークを処理するようにしようと努力してくれます（確か Work-Stealing でスケジュールしているんだったはず）。それでもGHCのランタイムは par が配列の構造に沿って二分法で行われているなどというのは知るよしもなく、実行時に動的に実行するので、狙ったような弱スケールはしないし、そもそも今回のベンチマーク設定でスレッドごとのデータサイズが一定になる保証も厳密にはなく、今回のコードに対して意味ある弱スケールのベンチマークをするのもむずかしい、というあたりでしょう。

というわけで、真面目に FFT を並列化したいなら、ちゃんと配列に沿ってスケジューラを書くべきですね。とはいえ、雑に書いたにしてはまあまあ並列化できているのは Haskell の強みでしょう。これ以上の改良は loop の実装をもうちょっと賢くするか、陽に Async のようなマルチスレッドライブラリ（のLinear版）を使ってがんばるのが現実的な解法でしょう。先に書いた通り、本記事のゴールは本当に高速な FFT を実装することではないので、これ以上は読者への課題とします。

トークンの他の応用例：線型資源の統一的なアロケーション

トークンの他の応用例には、線型リソースの統一的なアロケーションインターフフェースがあります。
これまで、配列を作成する fromList は以下のような継続渡しの形式になっていました。

fromList :: [a] -> (forall n. RW n %1 -> Array a n -> Ur b) %1 -> Ur b

これは、線型なリソースの束縛には外側の関数矢印が必要になるためでした。線型なデータごとにこういった継続渡しのアロケーションだけしか存在しないと、複数の種類のデータを組み合わせるのが困難になります。

こうした状況は、次のような Linearly トークンを導入することで大きく改善します：

data Linearly
instance Consumable Linearly
instance Dupable Linearly
linearly :: (Linearly %1 -> Ur b) -> b

data NewArray a where
  MkNewArray :: RW n %1 -> Array a n -> NewArray a

fromListL :: Linearly %1 -> [a] -> NewArray a

この詳細については、親記事の「複数資源初期化の問題──線型性トークンによる当面の回避策」の節で詳しく説明しましたので、参照してみてください。

API設計時の落とし穴：純粋な破壊的変更下での並列性について

先述のように、 par は GHC の spark# や seq# などという primops を使えば実装できます。
実際、私の開発している linear-extra ではまさにそのようにして実装しています。

ただし、気にしなければならない点がいくつかあります。線型型を使って破壊的変更を純粋な式にしている場合、評価順・回数に気を使う必要があるということです。
特に、GHC の最適化機構は、アグレッシヴに関数定義をインライン化します。ここで、もし破壊的変更がインライン化に伴って複製されてしまったりすると、本来順番に、一回ずつ実行される筈の変更が何度も任意の順で実行されることになりかねません。
par で並列化が入ってくると、par 自体が参照する
なので、以下の点に気を配る必要があります。

破壊的変更に対しては unsafeDupablePeformIO ではなく unsafePerformIO をつかったり、noDuplicate（や noDuplicate）などを使って副作用が複数回評価されないようにする。
副作用を含む途中式が最適化によって複製されないように、NOINLINE プラグマや noinline 魔法関数などを使う。
par など副作用を持ち得る純粋な並列計算コンビネータも同様。

API を設計する上でこれらをちゃんと念頭に置いてやるのはかなり骨が折れました。set に noDupable を使った上で NOINLINE を噛ませたりしても、最初の実装では並列に FFT を実行すると値がフッとぶというのがよく起きていたのです。最後にようやく par が複製されうる問題に気付いて、(3)に対処をし、やっと FFT が動くようになりました。私の linear-fft で runEval （par 内で呼ばれています）が noDupable# を使って実装されているのはこうした経緯です。

こうして汎用的な API を実装してみると、bytestring, vector そして linear-base などのように IO の中身にまで踏み込みながら大規模なライブラリを設計している人達の日頃の苦労には本当に頭が下がりますね……。

未来の Linear Haskell による Cooley–Tukey法

ややはなしが逸れましたが、2023年の Linear Haskell でいかにして純粋・並列・In-Placeな FFTが実現出来るかを見てきました。ここでは FFT を例に挙げましたが、これが一般的な配列の分割統治法アルゴリズムの並列化に応用できることはすぐにわかるでしょう^[11]。
リソースそのものを引き回すかわりにトークンを使って所有権の証拠とすれば、粒度の細かい所有権の借用の制御ができ、特に複製を伴わずに安全に配列のスライスを扱えるようになるのでした。

しかし、リソースを引き回さなくて済むようになったかわりに、結局トークンを引き回す必要があるのがイケてないところでした。これを解決すべく GHC への実装が提案されているのが、Linear Constraints です：

これは論文 "Linearly Qualified Types" を実装しようという（原著者らによる）提案です。これを使うことで、トークンの管理を線型な型クラス制約によって定式化することで、コンパイラが自動的にトークンの流れを推論・暗黙裡に引き回してくれるようになるのです！

論より証拠。先程の FFT の本体を Linear Constraints を使って書いてみた未来の Linear Haskell のソースコードが次になります：

data c /\ a where
  Box :: c %1 => a -> c /\ a

class R n
class W n
type RW n = (R n, W n)

fromListL :: Linearly %1 => [a] -> NewArray a
get :: R n %1 => Array a n -> R n /\ a
set :: RW n %1 => Int a -> Array a n -> RW n /\ a

class SlicesTo n l r
data Slice a n where
  MkSlice :: 
    (SlicesTo n l r, RW l, RW r) %1 => 
    Array a l -> Array a r -> Slice a n

halve :: RW n %1 => Array a n -> Slice a n
combine :: 
  (SlicesTo n l r, RW l, RW r) %1 =>
  Array a l -> Array a r -> RW n /\ Array a n

loop :: 
  RW n %1 => 
  Array (Complex Double) n -> Int -> Double -> 
  Double -> RW n /\ ()
loop rw arr !n !c !s
  {- ... -}
  let !half = n `quot` 2
      !dblCs = 2 * c * c - 1
      !dblSn = 2 * s * c
      !kW = c :+ s
      !(MkSlice lh rh) = halve arr
      (!(Box ()), !(Box ())) = 
        -- もしかしたら `par` にそれぞれのスレッドに貸し出す制約を
        -- 陽に教えてやらないとだめかも
        loop lh half dblCs dblSn
          `par`
        loop rh half dblCs dblSn
      !(Box arr) = combine lh rh
   in forN_ @(RW n)
        half
        ( \ !k ->
            let !(Box ek) = get k arr
                !(Box ok) = get (half + k) arr
                !(Box ()) = set k (ek + kW ^ k * ok) arr
             in set (half + k) (ek + kW ^ (half + k) * ok) arr
        )

forN_ :: forall c. Int -> (c %1 => Int -> c /\ ()) -> c /\ ()

すごい！ほとんど Rust みたいですね^[12]！RW n とか R n をトークンとして線型に束縛するかわりに、線型な型クラス制約としてあらたな矢印 %1 => の左側に置いて表現しています。

頻繁に型註釈に現れている型 c /\ a はほとんど Ur a と同じですが、オマケとして型制約 c が線型制約として一緒に返ってくるという違いがあります。いうなれば、「無限に^[13] a がはいっていて、オマケに制約 c が一個だけ入っている魔法の箱」という訳です。

ここで、これまでの & による局所束縛が消えて、let-束縛だけになったことに気付くかもしれません。これは「Linear Haskell の復習」節の最後で触れた linear let のおかげ……ではありませんね。あれは、線型資源の局所束縛時には %1 という接頭辞が必要でしたが、ここではついていません。ここではかわりに、Box へのパターンマッチが全て ! で正格評価させられています。どういうことでしょうか？

まず、Linear let の意義をちゃんと説明しておきましょう。

Linear let は、ひとことでいえば、「線型資源を使って別の線型資源を計算したときに、コンパイラにそれを明示するための機構」です。一方で、所有権トークンや Linear Constraints を前提とした可変配列のAPIでは、arr や lh, rh といった資源そのものは何回でも使える非線型なものとして与えられるのでした。なので、返ってきた値の ek や ok, それに () なんかの使用回数について GHC はハナから文句を言わないので、Linear let を使う必要はこの場合はないのです。

でも、型制約の RW n やら SlicesTo n l r やらが線型に消費されてるじゃんか！──目敏い読者の方はそう気付いたかもしれません。実は、線型な型制約は型推論によって受け渡し順が来まるので値とは別扱いされるのです。
具体的には、c /\ a の Box や Slice a n の MkSlice のように、線型な型制約を保持するデータ構築子については、! を使って正格パターンマッチを行ったときに限ってその線型制約が文脈に導入されるという仕様になっています。なので、上の例では線型な型制約を暗黙裡にやりとりする操作すべてに ! がついていたわけです^[14]。
これは、データ構築子についた型制約は隠れフィールドのようなものなので、それを評価することで文脈に入れたい、という気持ちもありますが、同時に ! がついた正確 let 束縛は定義順をまもって上から下に定義されるというGHCの仕様があるため、それにより実行順をちゃんと担保できるという副次的な効果もあります^[15]。

ところで、ここでは /\ にマッチするのに Box に対するパターンマッチが必要になるのはちょっと面倒臭いな、と思いますし、Skolem 変数のトリックを使うのに NewArray とか Slice みたいな存在型をいちいち定義しないといけないのは面倒だよなあと思うかもしれません。
原論文（や Linear Constraints の Proposal）では、別に提案されている第一級の存在型が GHC に入れば、これが更に簡潔に書けるようになります。

これは forall に加えて exists という存在量化子を GHC に実装して、更に、上の /\ をデータ構築子を陽には持たない GHC の特殊なプリミティヴ型として追加しようという壮大な提案です。
Dependent Haskell の生みの親である Richard Eisenberg らが書いた論文が元になっているものです。
これを使うと、上の例（の変更を受ける部分）は更に以下のようになります：

fromListL :: Linearly %1 => [a] -> exists n. RW n /\ Array a n

halve :: 
  RW n %1 => 
  Array a n -> 
  exists l r. (SlicesTo n l r, RW l, RW r) /\ (Array a l, Arrray a r)
combine :: 
  (SlicesTo n l r, RW l, RW r) %1 =>
  Array a l -> Array a r -> RW n /\ Array a n

loop :: 
  RW n %1 => 
  Array (Complex Double) n -> Int -> Double -> 
  Double -> RW n /\ ()
loop rw arr !n !c !s
  {- ... -}
  let !half = n `quot` 2
      !dblCs = 2 * c * c - 1
      !dblSn = 2 * s * c
      !kW = c :+ s
      !(lh, rh) = halve arr
      !((), ()) = 
        -- もしかしたら `par` にそれぞれのスレッドに貸し出す制約を
        -- 陽に教えてやらないとだめかも
        loop lh half dblCs dblSn
          `par` 
        loop rh half dblCs dblSn
      !arr = combine lh rh
   in forN_ @(RW n)
        half
        ( \ !k ->
            let !ek = get k arr
                !ok = get (half + k) arr
                !() = set k (ek + kW ^ k * ok) arr
             in set (half + k) (ek + kW ^ (half + k) * ok) arr
        )

Box やら MkSlice やらが消えてずいぶんスッキリしましたね！ほぼ Rust です^[16]！halve や combine, set, get の返値に ! はついているままですが、c /\ a を型に持つ値は暗黙裡に制約を隠し持っているので、上で Box に隠れている線型制約を表に引きずり出すのに必要だったのと同じ理由です。まあ、これくらいのボイラープレートなら許容できると思いますし、順番がちゃんと保証されるという自信を持つためにも ! を要求するのは妥当でしょう。

おわりに

という訳で、純粋・並列・Inplace FFT を題材にして、2023 年の Linear Haskell ではリソース本体から所有権をトークンとして切り離すことで、Rust の所有権をシミュレートできるということをまず見ました。

更に、現在提案が行われている Linear Constraints の GHC Proposal が実装されれば、Linear Haskell はほとんど Rust みたいになる^[17]ということがわかりました。

更に第一級の存在型が入れば、存在型や制約つきの型が GHC にビルトインで扱えるようになり、より自然な書き味になるのでした。

Linear Constraints については Core への変更がほとんどなく、既に簡単なプロトタイプ実装が存在するため、比較的はやく入るだろうことが予測されます。存在型についてはかなりの大改修が必要になりますが、いずれにせよ、「ほぼ Rust に近付いた Haskell」が使えるようになる日もそう遠い日のことではないでしょう。

とはいえ、本節で紹介したコードはあくまでも「未来の」Linear Haskell のもの、仮想上のものであり、まだどこでも使えるものではありません。この「未来」を「現実」に近付けるためにも、上の GHC Proposal に 👍 をしたり、Proposal を読み込んでフィードバックをしたりしていきましょう。未来は我々の手で切り拓くのです！

また、今回は可変配列に焦点を絞りましたが、親記事の末尾でも触れたように Linear Haskell の射程はもっともっと広いものです。
気が向いたら是非 Linear Haskell や Linear Constraints の原論文、提案者らのいる Tweag のブログ記事、彼等が開発している linear-base などを覗いてみてください。必ず発見があると思います。

https://arxiv.org/abs/1710.09756

https://arxiv.org/abs/2103.06127

特に、今回の主題である Linear Constraints については以下の公式ブログポストが参考になります：

あと、もしよければ私が空き時間に実装を進めている linear-extra にも触ってフィードバックをもらえると嬉しいです。トークン回りがあつかえるライブラリは（そのうち Linear Constraints が入って要らなくなるだろうとみんな思っているからか）私の知るかぎりこれしかないです。

https://github.com/konn/linear-extra

皆さんも「Linear Haskell でこんなの作ってみたよ！」というような発信をどんどんやって、用例を積み上げていこうではありませんか！

ではではこんなところで。Have a Happy Futre Linear Haskelling and New Year!

脚注

なんと、最後に Haskell Advent Calendar に参加してから9年ぶりらしい^[2]です。出戻りですけど、宜しくね。 ↩︎
Qiitaを退会していたためか、アップロードが盛大に遅れたためか、登録されている筈の Haskell Advent Calendar 2014 には名前が載っていないですが、一応参加作品です。 ↩︎
$O(N \log N)$ で ↩︎
解法には他にもいろいろありますが、一番有名なのは Cooley–Tukey なのと、僕が Cooley–Tukey しかちゃんと知らないので、Cooley–Tukeyをえらびました。 ↩︎
ところで、アルゴリズムの文脈での in-place って日本語の定訳ってあるんでしょうか？ ↩︎
厳密には、前処理で高速なビット反転を行うには補助的に長さ $\log(N)$ の整数配列が必要になりますが、log がついてるのでゴミみたいなもんですし、前処理が終わったら使わないので安全に解放できます。 ↩︎
ここでは、RankNTypes の Skolem 変数を使った ST モナドはふつうの Haskell の範疇と見做しています。余談ですが、私が Haskell をはじめた頃にちょうど青木峰郎さんの『ふつうの Haskell プログラミング』が出て、とてもお世話になりました。えっもう17年も前の本ってまじですか……？ ↩︎
Skolem（スコーレム）は20世紀中盤にかけて活躍した数理論理学者です。STモナドなどRank-N多相の文脈で "Skolem variable" という用語がどのような経緯で使われるようになったのか筆者はよく把握していませんが、述語論理からの存在量化子の消去や Löwenheim–Skolem の定理の証明などに使われる Skolem function, Skolemisation という概念があり、それが由来なのだろうと勝手に思っています。 ↩︎
注意深く読んでいる人は、パフォーマンスについて、何か気付いた人がいるかもしれませんね。まあ、待ってください。 ↩︎
また、トークンたちには実体がないので、ZeroBitTypeカインドを持つようにしておけば、トークンの引き回しが実行時間に与える影響を完全にゼロにすることができます。 ↩︎
実際、原論文で紹介されているのは（直列な）Quicksort の純粋な実装だったりします。 ↩︎
個人の感想です。 ↩︎
厳密を期すなら「任意有限個の」と言うべきですが、魔法っぽさを重視して「無限の」としました。 ↩︎
対して、half から kW までについている ! は特に線型型とは関係ありません。ヘンなところでサンクができないように、習慣的に ! をつけているだけです。これも Complex の全フィールドは正格なのでたぶん kW にだけ付ければほとんど十分なはず（だし、その後書き込まれる配列が Storable なり Unboxed なりならそれも kW も不要なはず）ですが、まあ手癖ですね。 ↩︎
というか、Linear Haskell ではパターンマッチを含む線型な変数束縛は正格でなくてはならないという仕様があります。これは、通常のパターンマッチでは各フィールドが遅延評価されてしまって実質フィールドの射影関数をとっているのと同値になってしまうからです。射影関数は部分的にデータを捨ててしまうので、これは線型性を破ってしまう。なので、パターンマッチは正格でなくてはならないという訳です。 ↩︎
個人の感想です2。 ↩︎
個人の感想です3。 ↩︎

Discussion

Hidden comment