バレンタインのお返しを最大化するスマートな方法

今日はバレンタインなのでこの記事を書きます。書き終わってる頃にはバレンタインじゃなくなってるかも。まぁ、そんなことはどうでもいいんです。

初めに

この記事は、「アルゴリズムってすごい！」ってことを伝えるための記事です。そのため、緑コーダー以上は読んでも何も得られないどころか、より良いアプローチを思いついてイライラしてしまうかもしれません。(n≦10^5でも普通に解けますね)

さて、この記事に出てくるこかすた〜君は、なるべく少ない手間でより美味しいチョコレートをお返しにもらいたいようです。バレンタインをそういう風に見るのは良くないですが、問題なので仕方ないです。こかすた〜君はこの願いを叶えるため、以下のような問題を考えています。

問題

こかすた〜君はn人の友達がいます。
i番目の友達(1≦i≦n)にチョコをあげると、お返しとしてコストA[i]のチョコをもらえます。
また、こかすた〜君はj人分(0≦j≦n)のチョコを用意するのに、コストB[j]かかります。
このとき、もらったチョコのコストの総和 - 用意するのにかかったコストの最大値はいくつでしょうか?

制約

値はこの範囲内に収まることが保証されます。

1≦n≦20
1≦A[i]≦10^8
1≦B[i]≦10^9

入力

入力は以下のように与えられます

n
A[1] A[2] ... A[n]
B[0] B[1] ... B[n-1] B[n]

出力

もらったチョコのコストの総和 - 用意するのにかかったコストの最大値を出力してください。

例

入力

お返しには、1人目はコスト4、2人目はコスト2、3人目はコスト4のチョコを用意してくれているようです。
また、こかすた〜君は0人分のチョコを用意するときはコスト0、1人のときは2、2人のときは3、4人のときは6かかるようです。

3
4 2 4
0 2 3 6

出力

コスト3でチョコを2人分用意し、1番目の人と3番目の人にチョコを渡すことで、(4+4)-3=5で最大になります。

5

少し考える

さっそく、問題について考えてみます。

まずは単純に

この問題を解く方法として、すべての渡し方をシミュレーションする方法が考えられます。
つまり、「誰にも渡さない」「1番目」「2番目」「3番目」「1番目と2番目」...のように順番に考えて行くことです。

この方法は確かに解けそうです。人数も最大20人ですから、そんなに時間はかからないでしょう。
でも、この場合どういう風に考えればよいでしょうか? 「n人から２人ペアを選ぶ」であれば、以下のようにプログラムを書くことで選べます。

for(int i=0;i<n;i++){ //ペアの左側を何番目にするか決める
    for(int j=i+1;j<n;j++){ //ペアの右側を何番目にするか決める
        //ペアの右側は必ず左側よりひとつ以上右になるので、jは最初はi+1から始める
        printf("%dと%dのペア",i,j);
    }
} 

このようなfor文を「2つ選ぶ場合」「3つ選ぶ場合」「4つ選ぶ場合」...と準備すれば確かにできるかもしれません。
でも、スマートではありません。もっといい方法があるはずです。

表にして考えてみる

ここで、少ない数で考えて表にして考えてみましょう。
2人にチョコを渡す方法は「誰にも渡さない」「1番目に渡す」「2番目に渡す」「1番目と2番目に渡す」の4通りです。
これらを、渡す場合=1、渡さない場合=0で表にしてみます。

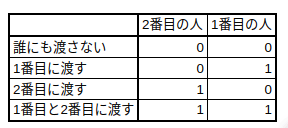
「00,01,10,11」の並び、どっかで見たことがあります。そう、2進数です。
では、3人の場合はどうでしょう。これも表にしてみます。

少し順番がややこしいですが、000から始まり111まで2進数になることがわかります。

このように2進数になることを逆手に取り、2進数の位の0/1を使うことで、この全探索は簡単に考えることが可能です。
n個の中から好きなように選ぶ方法を、n桁の2進数で調べ上げるこのアルゴリズムを「ビット全探索」といいます。

ビット全探索を使って実際に解いてみる

ここまでで、「アルゴリズムすごい！！」「こんな発想があるのか！」と思っていただけたら幸いです。
このようなアルゴリズム力は、競技プログラミングをすることで養えます。興味のある人はE869120さんの素晴らしい記事と、わかりやすいC++入門を使ってぜひ取り組んでみてください。

ここから先は、C++という言語を使って実際に問題を解くプログラムを作ります。この記事の本題は、僕も初めて知ったときに味わった「ビット全探索すごい！こんな発想があるんだ！」を共有したいだけですので、これ以上は読まなくても問題ないです。(最後に　だけ読んでくれると嬉しいかな)

入力

いつものincludeなどなども込みです。C++やったことない人は特に気にせずmain関数を見てください。
まずはnを受取、その後長さnの配列A、長さn+1の配列Bを用意し、そこに値を入れています。
Aに関しては、添字が入力のところとずれている(入力では1スタートで、配列は0スタート)であることに注意が必要です。

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n;
    cin >> n;
    vector<int> A(n),B(n+1);
    for(int i=0;i<n;i++){
        cin >> A[i];
    }
    for(int i=0;i<n+1;i++){
        cin >> B[i];
    }
    int ans = INT_MAX*-1;
}

最後に、答えを格納するans変数を用意しました。なるべく大きい値に更新するために、初期値はintの最小値にしてあります。
ここから先は、main関数の続きを書いていくことにします。

すべての2進数を列挙する

C++では、bitsetという機能を使うことで、2進数を簡単に扱えます。2進数に簡単に変換できるだけではなく、特定の桁が1なのかどうかの判定なども簡単に行えます。
bitsetの使い方は先程も紹介したC++入門で僕は勉強しました。

n人のすべての選び方は、000...0と0がn個並んだ2進数から111...1と1がn個並んだ2進数までで表せることは先程やりました。。つまり、111...1(1がn個)通りあるわけです。
「1をn個並べた数」はいくつなのでしょう? C++は、1<<nとすることでその数を簡単に求められます。
また、bitset<桁数>という型の変数にint型変数を代入すると、指定した桁数の2進数に変換してくれます。この桁数は変数として指定ができないので、nの最大値である20を使います。
こうすることで、000...0から111...1まですべてを列挙できます。

for(int i=0;i<(1<<n);i++){
    bitset<20> b = i;
}

こうすると、bには000...00→000...01→000...10→...→111...11という値が入っていくわけです。
次は、各桁ごとに1か0かをチェックして処理をしていきます。ここから先はforの中身だけ書きます。

桁ごとにチェック

まずは、お返しのチョコのコストの総和を記録するcost変数を用意します。
次に、0桁目~n桁目まで順に、「その桁が1であるかどうか」をチェックします。bのi桁目が1である場合b.test(i)がtrueになります。なお、配列同様0から始まります。
桁が1であった場合その人からチョコがもらえますので、costに足しましょう。

bitset<20> b = i;
int cost = 0;
for(int j=0;j<n;j++){
    if(b.test(j)){    
        cost += b[j]; //j+1番目の人からチョコをもらうので、足す
    }
}

自分のチョコのコストを計算する

bitsetでは、b.countで1が何個あるのかがわかります。それにより、自分がチョコを何人分用意するのかがすぐわかります。そこから、自分のかかるコストを求められます。
あとは、cost変数から用意するコストを引いた値を、現在の暫定値と比較してあげます。もしも暫定値より高いコストであれば、更新してあげましょう。

bitset<20> b = i;
int cost = 0;
for(int j=0;j<n;j++){
    if(b.test(j)){    
        cost += A[j]; //j+1番目の人からチョコをもらうので、足す
    }
}

int myCost = B[b.count()]; //b.count()個のチョコを渡すときのコスト
if(ans < cost-myCost){
    ans = cost-myCost; //もし今の答えよりもよかったら、更新
}

最後に、それを000...0から111...1までやれば全探索したことになるので、その時点でのansがそのまま答えになるわけです。出力しましょう。

プログラムまとめ

全体はこんな感じになります。

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n;
    cin >> n;
    vector<int> A(n),B(n+1);
    for(int i=0;i<n;i++){
        cin >> A[i];
    }
    for(int i=0;i<n+1;i++){
        cin >> B[i];
    }
    int ans = INT_MAX*-1;
    
    for(int i=0;i<(1<<n);i++){
        bitset<20> b = i;
        int cost = 0;
        for(int j=0;j<n;j++){
            if(b.test(j)){    
                cost += A[j]; //j+1番目の人からチョコをもらうので、足す
            }
        }
        
        int myCost = B[b.count()]; //b.count()個のチョコを渡すときのコスト
        if(ans < cost-myCost){
            ans = cost-myCost; //もし今の答えよりもよかったら、更新
        }
    }
    
    cout << ans << endl;
}

間違ってたらごめんなさい(おい)

最後に

アルゴリズムは奥が深いんだよ！！　ってことを伝えたいです。

プログラミング力あるのにアルゴリズム力がないのは残念なことだと僕は思います。アルゴリズム力はプログラミングの確かな基礎となってくれます。みなさんやりましょう、競プロを！
そして、プログラミングで特にやりたいことがない！って人も、競プロをやると、きっと将来役に立つと思います。