バレントロピー (varentropy) について

バレントロピー (varentropy) について

はじめに

最近話題になったEntropixですが、バレントロピーに馴染みがないので例の4象限がいまいちピンと来ませんでした。ということでバレントロピーの性質について調べてみたいと思います。

Entropix

Entropixについてはいろいろ記事が出ていますが、EntropixplainedはLLMの基本から書かれていて良いと思います。

まずはエントロピー (entropy) について復習

確率変数$X$がそれぞれ$p_1, p_2, ..., p_n$（ただし、$\sum_{i=1}^n p_i=1$）の確率でn通りの値を取り得るとします。このとき$-log_2(p_i)$を$X$がi番目の値を取る事象の自己エントロピーといいます。これは言わばその事象が生起することのビックリ度の指標であり、$p_i$が1つまり確実に起きる事象が起きた時のビックリ度はゼロであり、$p_i$がゼロに向かって小さくなっていくにしたがって無限大に向かって大きくなっていく、つまりあまり起きるの思っていなかった事象のビックリ度は大きくなります。

例としてA国の大統領選に2人の候補T氏とH氏がいて、それぞれ当選確率が50％だとします。この場合どちらの候補の勝利の自己エントロピーも$-log_2 0.5=1$となります。また別のR国の大統領選にはP氏、S氏、D氏の3人の候補がいたとします。R国は実態は独裁国家であり、大統領選は出来レースで実質的な独裁者P氏の勝利する確率は99.9995%、S氏の勝利する確率は0.0004%、D氏の勝利する確率は0.0001%だったとすると、P氏勝利の自己エントロピーは$-log_2\ 0.999995\approx7.2\times10^{-6}$（ほとんどまったくビックリしない）、S氏勝利の自己エントロピーは$-log_2\ 0.000004\approx11.3$（とてもビックリ）、D氏勝利の自己エントロピーは$-log_2\ 0.000001\approx20$（もっととてもビックリ）となります。

そして、エントロピーは自己エントロピーを各事象の生起確率で加重平均したもの$H(X)=-\sum_{i=1}^np_ilog_{2}\ p_i$、すなわち自己エントロピーの期待値として定義されます。つまり期待ビックリ度です。エントロピーは情報量の尺度であり、シャノンの情報量とも呼ばれます。

先ほどの例で計算すると、A国の大統領選のエントロピーは$-(0.5\times log_2\ 0.5+0.5\times log_2\ 0.5) = 0.5\times 1 + 0.5\times 1=1$でありR国の大統領選のエントロピーは計算は省略しますが約$1\times 10^{-4}$となります。

さて、先ほどからシレっと2を底とした対数$log_2 p$を使っていますが、情報量としてのエントロピーではこれを使うことが多いです。2を底とした対数で計算した（自己）エントロピーは単位をbitで解釈することができるのでわかりやすいからです。例えば50%の確率の事象の自己エントロピーは1bitですが、これは同じ確率で起きる2通りの事象の中の1つが起きるのに相当するビックリ度というわけです。エントロピーはもともと物理学から出てきた概念ですが物理学では自然対数を使うようです。

$n$が与えられたとき、エントロピーは全事象が同じ確率で起きるとき ( $p_i=1/n, i=1,2,...,n$ )に最大になります。証明は省略しますが、ラグランジェの未定乗数法で証明できます。逆に事象が確定的な場合、つまり$p_i$のどれかひとつが1で残りがすべてゼロのときはエントロピーは最小値0となります。$p=0$のときの自己エントロピーは$-log_2 0=\infty$となりますが$p log_2 p → 0 \ (p → 0)$なのでエントロピーの計算においては無視できます。先ほどの例ではA国の大統領選は前者で、R国の大統領選は後者に近いものと言えます。

バレントロピー

バレントロピーは自己エントロピーの分散であり、$V(X)=\sum_{i=1}^np_i(-log_2p_i-H)^2$で与えられます。大統領選の例で計算してみるとA国の大統領選では$0.5\times(-log_2 0.5-1)^2 + 0.5\times(-log_2 0.5-1)^2 = 0.5\times(1-1)^2 + 0.5*(1-1)^2 = 0$となり、R国の場合は計算式は省略しますが、約$0.0017$となります。

バレントロピーは分散なので非負となりますが、自己エントロピーが100%エントロピーと等しくなる場合は$0$で最小値となります。これはあらゆる事象が等しい確率で起きる場合（$p_i=1/n$）と事象が確定的な場合（ある$k$について$p_k=1$、$i\ne k$のとき$p_i=0$）に相当します。大統領選の例ではA国の場合のバレントロピーは前者に相当し、R国の場合はほとんど後者に近いのでバレントロピーは大変小さな値となっています。

それでは$n$が与えられた時、バレントロピーはどのような場合に最大値となるのでしょうか？数値的に計算してみましょう。以下は用いたコードです。

from typing import Optional, Callable
import numpy as np
from numpy.typing import NDArray
from scipy.optimize import minimize
from einops import rearrange, repeat, pack
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

def init_p(n: int, k: Optional[int]=None, perturbation: float=0) -> NDArray[np.float64]:
    if k is None:
        p = np.ones(n)
        if perturbation > 0:
            p += np.exp(np.random.normal(0, perturbation, n))
        
        p /= p.sum()
        return p
    else:
        p = np.zeros(n)
        p[k] = 1
        return p

eps = 1e-10

def binary_entropy(p: NDArray[np.float64]) -> float:
    positive_mask = p > 0
    pp = p[positive_mask]
    return -(pp*np.log2(pp + eps)).sum()

def binary_varentropy(p: NDArray[np.float64]) -> float:
    positive_mask = p > 0
    pp = p[positive_mask]
    return (pp*(-np.log2(pp + eps) - binary_entropy(pp))**2).sum()

n = 10
p0 = init_p(n, perturbation=1)

def loss_fn(p: NDArray[np.float64]) -> float|NDArray[np.float64]:
    return -binary_varentropy(p)

result = minimize(loss_fn, bounds=[(0, 1)]*n, constraints=({"type": "eq", "fun": lambda x: x.sum() - 1}), x0=p0, tol=1e-10)
print(result.x)

# [0.02378818 0.02378821 0.78590655 0.02378819 0.02378819
# 0.02378826 0.02378793 0.0237882  0.02378814 0.02378815]

$p_3\approx 0.786$、$i\ne3$について$p_i\approx 0.238$となっています。どうやらバレントロピーは高確率の事象ひとつと確率の等しい残りの事象にいい按排に分離したときに最大になるようです。それでは$p_0$を$1/n$から$1$まで$0.01$刻みに変化させてバレントロピーを計算し、結果をプロットしてみましょう。コードはノートブック上に上の続きで書くものと思ってください。

（追記: einops.repeatとeinops.packを使って書換えたらとてもシンプルになりました。すみません、einopsニワカなもので）

step = 0.01
p_0 = np.arange(1/n, 1 + step, step)
p_r = (1 - p_0) / (n - 1)
num_cases = p_0.shape[0]
# p_mat = rearrange(
#     [p_0] + [
#         x for x
#         in rearrange(p_r, 'c -> 1 c')*np.ones((n-1, num_cases))
#     ],
#     "n c -> c n"
# )
p_mat, _ = pack([p_0, repeat(p_r, "c -> c r", r=n-1)], "c *")
vs = np.array([binary_varentropy(p) for p in p_mat])

fig = plt.figure()
ax = fig.add_subplot(111)
sns.lineplot(x=p_0, y=vs, ax=ax)
ax.set_xlabel("p_0")
ax.set_ylabel("Varentropy")

Entropixの4つの象限は典型的にはそれそれどういう場合なのか？

これまでに得られた知見を踏まえて、Entropixの4象限の図を眺めてみましょう。

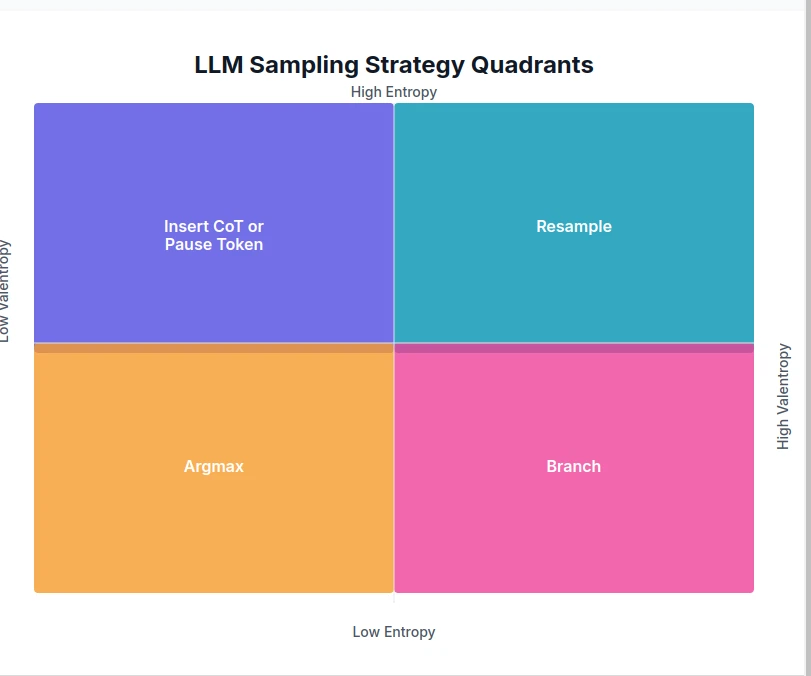
• バレントロピーが低い場合というのは、先ほど作った$p_0 - varentropy$のプロットの両端付近に当たります。
• そのうち、エントロピーが高いつまり左上の象限はプロットでいうと左端付近、すなわち各事象の確率が$1/n$で等しい場合に相当します。この場合Insert COT or Pause Tokenというアクションが取られるわけです。
• 一方でプロットの右端付近、つまりほぼ確定的な状況ではエントロピーが$0$に近くなります。これは左下の象限に該当し、Argmaxというアクションが取られます。次に来るトークンはほぼ確定的にわかっているわけですから、これを採用するという当たり前のアクションですね。
• バレントロピーが高いのはプロットの右の方の山のてっぺんあたりですが、このあたりではエントロピーは低いですから、右下の象限というのは典型的にはこのプロットのてっぺんあたりと考えることができるでしょう。この場合はBranchというアクションが取られます。

エントロピーもバレントロピーも高い状況というのはちょっとわかりにくいです。上でscipy.optimize.minimize()を使って$-V$を最小化しましたが、今度は$-w*H-(1-w)*\sqrt{V}$をwを$0$から$1$まで変化させてそれぞれ最小化してみましょう。

w_array = np.linspace(0, 1, 11)
print(w_array)

# [0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]

p_list = list()
for w in w_array:
    def loss_fn(p: NDArray[np.float64]) -> float|NDArray[np.float64]:
        return -w*binary_entropy(p) - (1 - w)*np.sqrt(binary_varentropy(p))

    result = minimize(loss_fn, bounds=[(0, 1)]*n, constraints=({"type": "eq", "fun": lambda x: x.sum() - 1}), x0=p0, tol=1e-10)
    p = np.sort(result.x)
    p_list.append(p)

p_mat = rearrange(p_list, "w n -> w n")
p_df = pd.DataFrame(np.log2(p_mat), index=[f"{w:.1f}" for w in w_array])
sns.heatmap(p_df)

グラデーションがわかりやすいように$log_2$を取っていることに注意してください。下から見ていくと$w=1$のとき、つまりエントロピーのみ最大化した場合はすべての$i$について$p_i=1/n$となります。そして$w$が小さくなるにしたがってテールの部分の確率が低下していき、ヘッド（右端）の確率が上昇していくことがわかると思います。右上の象限は「ヘッドに確率が集中しながら適度にテールにも確率が分散している状態（ただしバレントロピー最大の時よりテールの配分が大きい）」ということができるでしょう。