Open2021/08/15にコメント追加9

Unity/VCIで物体を常に正面に取りたい。三角関数からクォータニオンまでの道のり

線形代数学

VCIで常にカメラの正面に配置されるオブジェクトを作りたくて、SetRotation/GetRotationを見てたらQuaternionと言う謎の4次元のデータ構造を取り扱っている。どうやら、Unity由来っぽいけど説明読んでもサッパリ分からない…

Quaternion自体は一般概念みたいなので適当にググってみたけど、オイラー角とかさらに知らない単語が。。。

基礎知識が無さ過ぎて何が分からないかもわからないので、ちょっと高校数学というか三角関数の基本的な使い方から座標系の勉強をし直したメモ。やはりゲームは数学（というか物理）か。。。

距離と角度から三角関数で座標を求める

「三次元なんぞクソ！二次元こそ至高！」というのは冗談だけど、いきなり三次元は分けわからなくなるので2次元から。

とりあえず物体そのものの角度は忘れて平面での座標系だけ考える。静止衛星のように常に正面を向いていると言うことは円運動になるはずで、その座標は2次元では三角関数で求まったよね？とGoogle先生と対話しながら思い出した。

自身の角度や相手との距離はVCIのAPIで取得できるので必要なのはXY座標。という分けで距離と角度から直交座標を求めるのは以下のように三角関数を使う。意外と社会に出てからも役立つ＞＜＃注：個人差があります

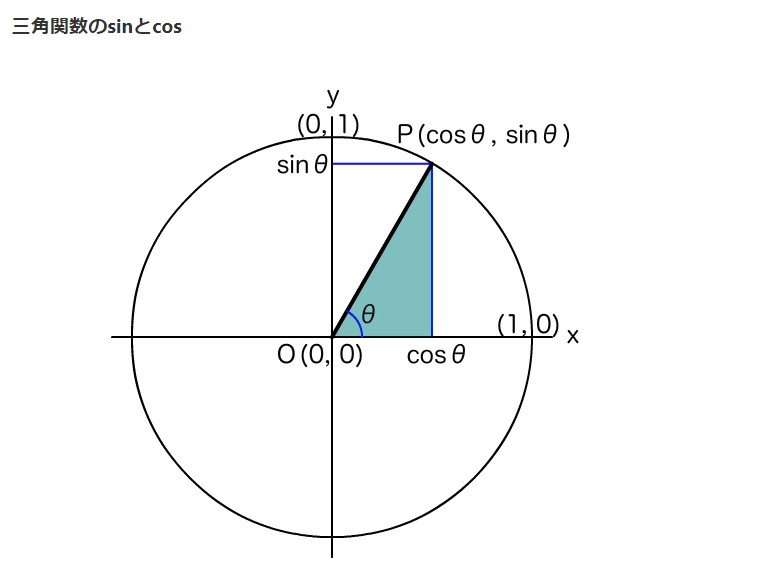
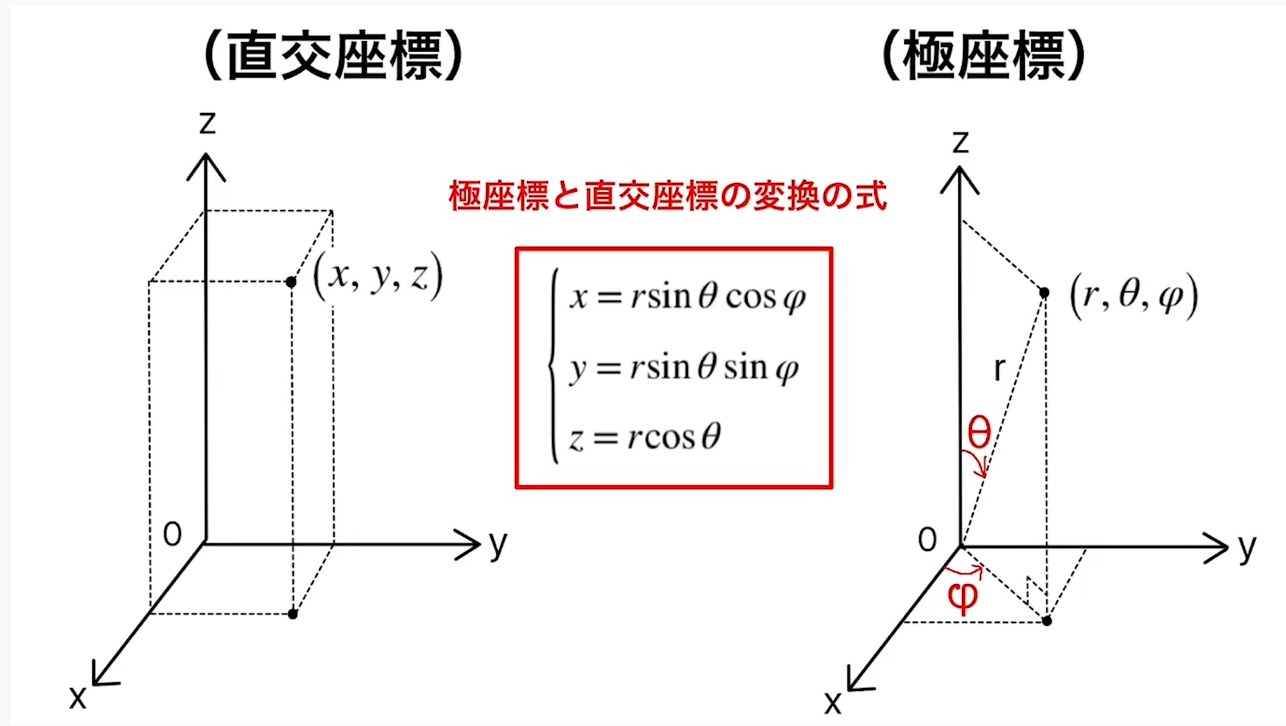
原点(0,0)からの距離rとx軸正方向となす角度θから座標(x,y)を求められる。

x = r cosθ
y = r sinθ

なお、座標の計算は下記サイトが便利。グラフを描画してくれるし神では？

https://www.geogebra.org/3d?lang=ja

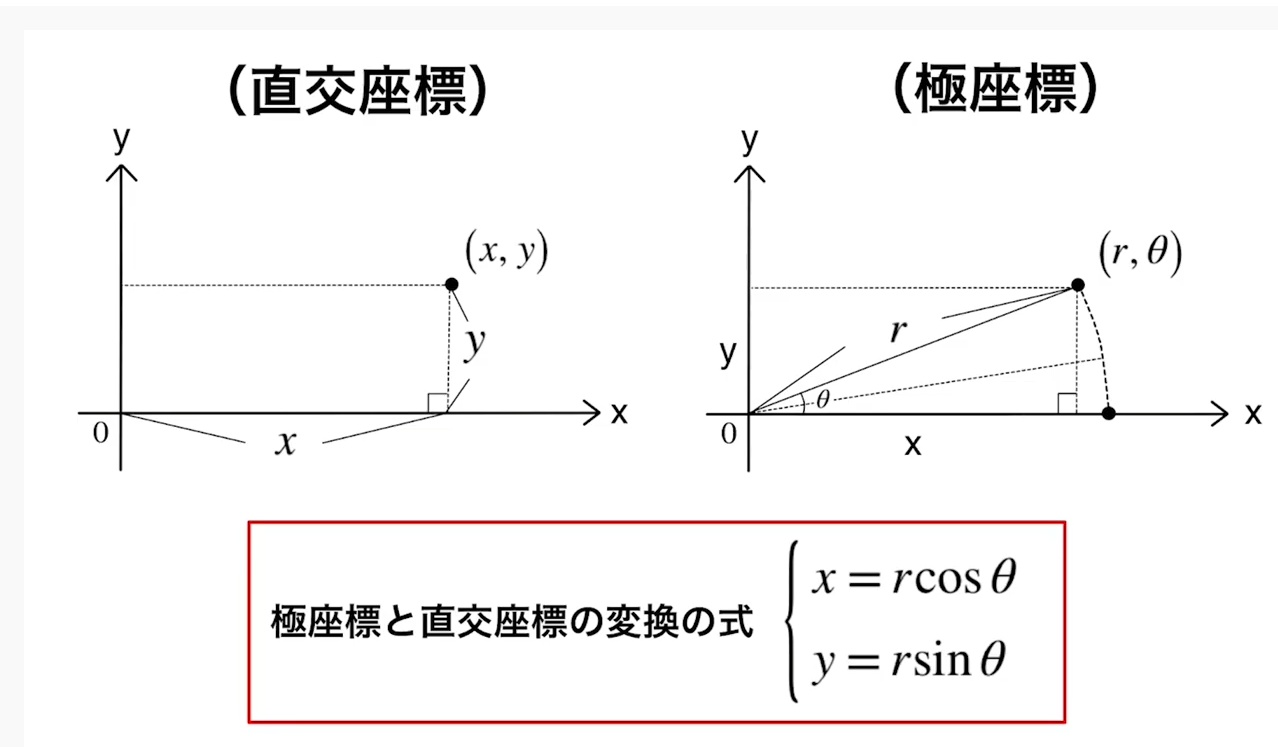
直交座標と極座標

あと、距離と角度で表す座標系を極座標と呼ぶらしい。たぶん、この用語を知らないとこの後調べ方が分からなくなる奴。

2次元

3次元

角度(radian/degree)、回転行列、オイラー角、クォータニオン (Quaternion)

3次元の回転を表す方法について。

回転行列

2次元の回転行列

回転行列、座標変換マトリクスとも言うらしい。
ある座標を角度βずらすt目に必要な行列が回転行列。2次元や3次元などに適用する事が出来る。

まずP(x,y)の座標を極座標で表現すれば

P = [
x = r cos α
y = r sin α
]

となる。同様にそこからβずれた座標Q(x', y')の極座標は

Q = [
x' = r cos (α + β)
y' = r sin (α + β)
]

となる。加法定理により（α ＋ β）を展開すると下記のようになる。

Q = [
x' = rcos α * rcos β - rsin α * rsin β)
y' = rsin α * rcos β + rcos α * rsin β)
]

上記の式に

[
x = r cos α
y = r sin α
]

を代入すると

Q = [
x' = x * rcos β - y * rsin β
y' = y * rcos β + x * rsin β
]

これを共通因数[x,y]でくくって因数分解すると

これが角度βずらす2次元の回転行列

３次元の回転行列

3次元の回転行列も考え方は2次元と同じ。ポイントとしてはいきなり任意の3次元座標への回転を考えず、X, Y, Zそれぞれの軸を固定して計算する。

例えばZ軸を回転軸として考えた場合は実質的にはXY平面となり以下のように求める事が出来る。

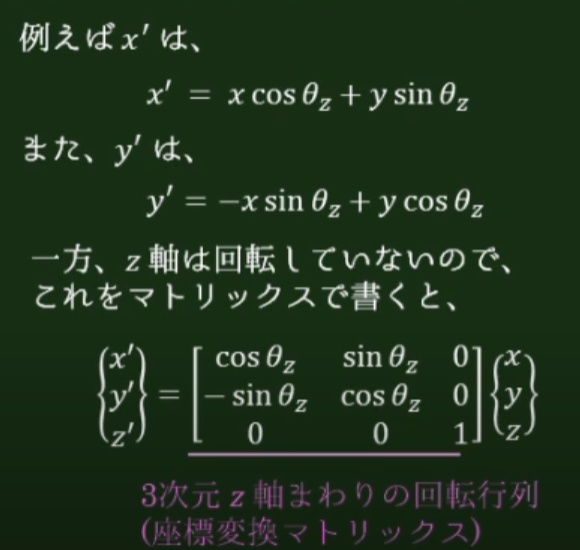
同様にX軸周りとY軸周りをそれぞれ考えると以下のようになる。

最終的にそれぞれを全て掛けてしまえば3x3の9要素でθx, θy, θz傾けた場合の任意の座標を求める事が出来る。

オイラー角

オイラー角はx, y, zの3軸に対してそれぞれ角度を入れる考え方。イメージしやすいが計算が難しかったり、ジンバルロックという問題が合ったりするらしい。
UnityでRotation に指定している値はオイラー角。ただし、内部的にはQuaternion に変換されている。

Quaternion/四元数

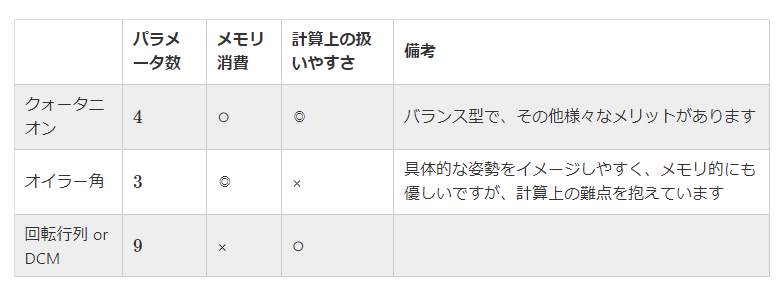
オイラー角と違いジンバルロックが起こらず計算もシンプル、回転行列に比べてパラメータが少なくてメモリに優しい、そんなUnity/VCIの内部で使われてるのがQuaternion。

ref: クォータニオン (Quaternion) を総整理！～三次元物体の回転と姿勢を鮮やかに扱う～

四元数は複素数を拡張したものらしい。

複素数

そもそも複素数ってなんだっけ、と言う話。iの二乗が-1が虚数の定義ではあるけれど。

複素数において(1, 0)は1と表現するし、(0, 1)はiと表現する。

複素数と二次元ベクトルは名前が違うくらいに勘違いして覚えてたんだけど、加法は同じだが乗法の特性が全く異なる。

足し算はこう。平行四辺形になる。

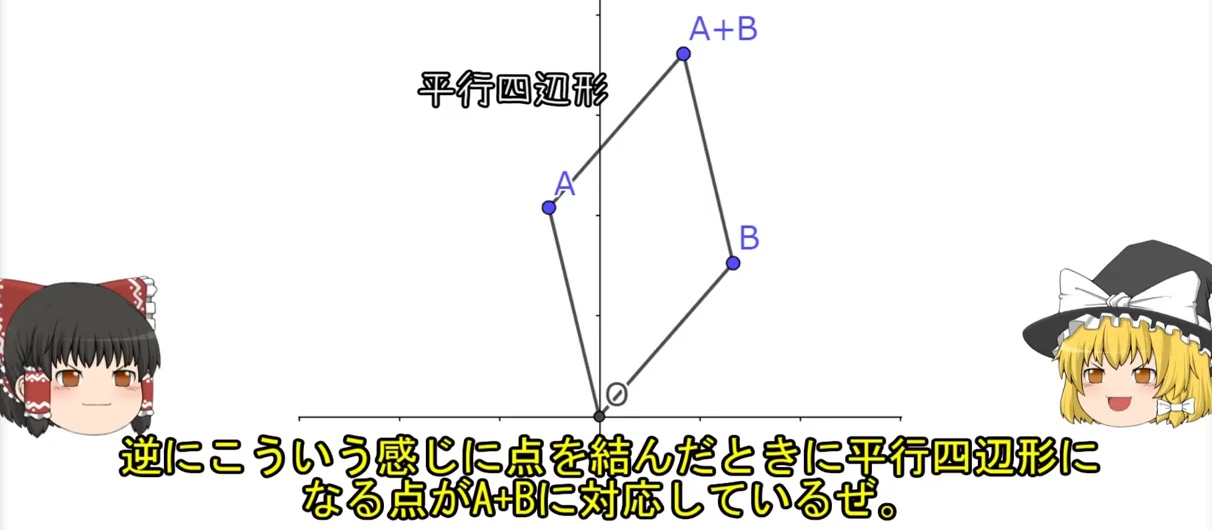
掛け算は回転を表す。なんか回転行列で見た感じの説明に。

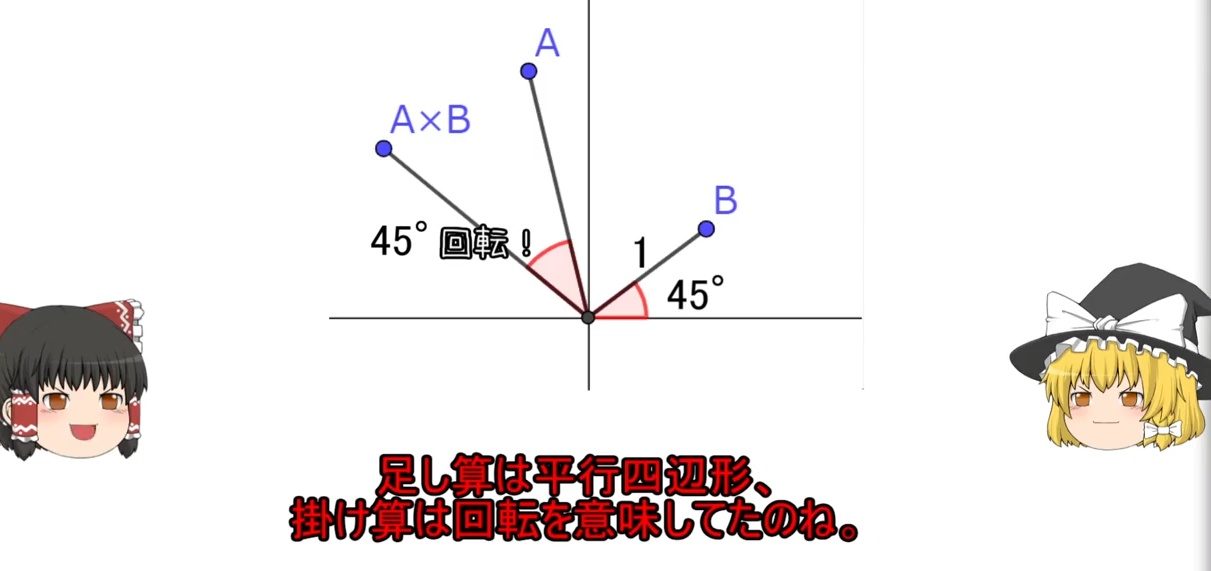
これをベースに考えるとi^2が-1になるのは以下のように直観的に理解できる。

まずiを掛けるというのは90°回転させるということ。

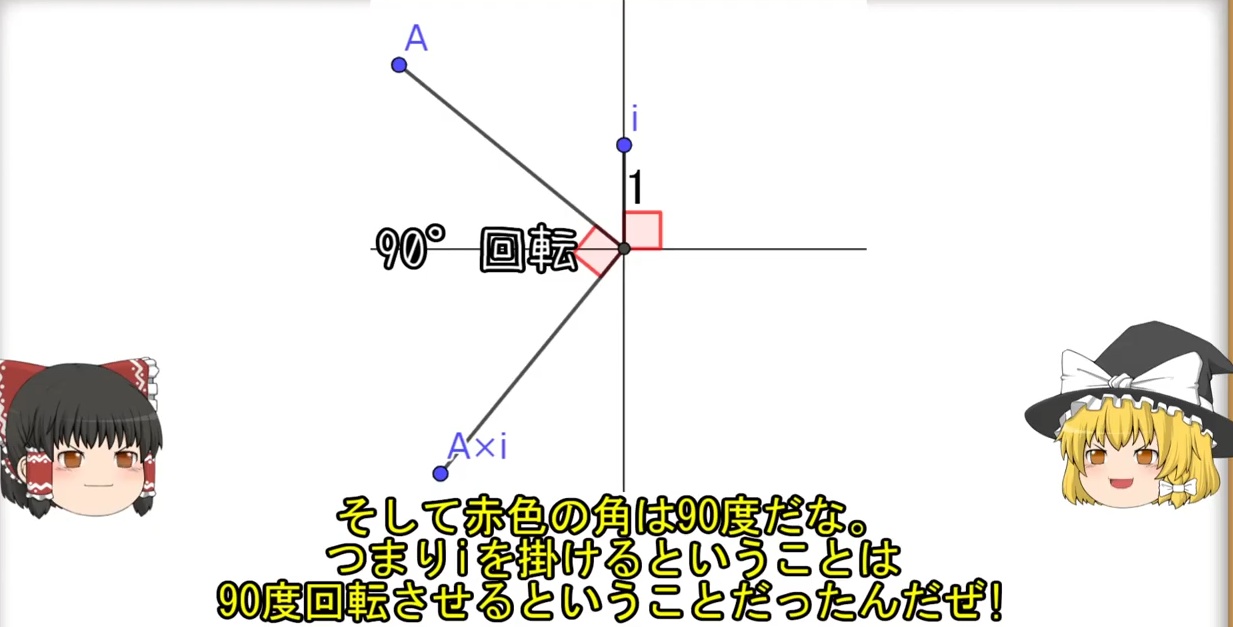
元々(0, 1)つまり、原点から垂直に縦方向に存在しているのがiなので、これにiを掛けると90°進んで180°、つまり横軸である実数の-1になる。

つまり複素数の掛け算は平面上での回転を計算することができ、これは以下のように循環する。

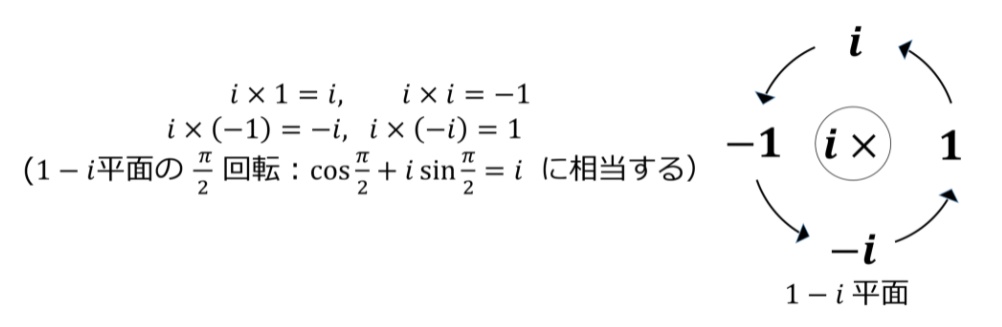
ref: クォータニオンとは何ぞや？：基礎線形代数講座

四元数

複素数は平面の回転を計算できたので、それを空間に拡張するために更なるパラメータjを導入。ただし、これは計算の法則が崩壊するのでさらにkを導入して空間の回転を含めて表現出来るように下のが四元数。

3元数では1-i平面(xからyへの回転)と1-j平面(xからzへの回転)は表現できるがi-j平面(yからzへの回転)で計算に矛盾が生じる。

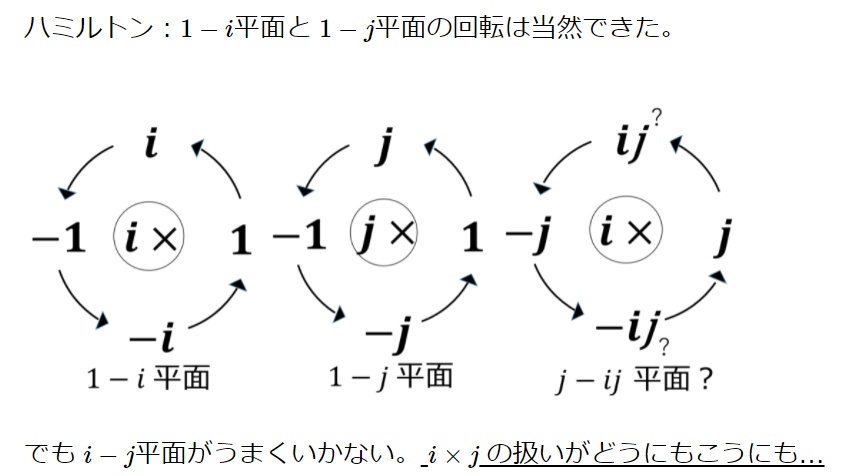
そのため、ij=kという定義のkを導入する。

これで以下のようにijも含めて適切に計算でき循環する

一連の話はAicia Solid Project さんの動画でまとまっている。さすが。

3次元の距離

A=(1,1,1)
B=(3,4,5)

AB = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2}

VCIで扱うときにはスクリプト上でもオイラー角で取り扱えるっぽい。

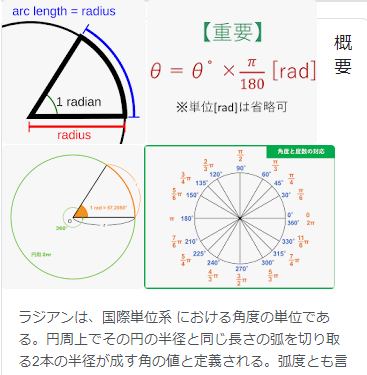
Luaの三角関数の引数は角度ではなくラジアン。
angle = LeftScreen.GetRotation().eulerAnglesでとれるのは角度なので変換をするのが必要。