💾
過学習からLLMへ

2023/04/24に公開
ディープラーニング
 0.前書きはじめまして。株式会社Knowhere CTOの今井と申します。
私たちは、「誰もがスポーツが上手くなれる環境を」をミッションに掲げ、AIなどのテクノロジーの力を用いたソフトウェア等の研究開発を行なっています。
テック企業の一員として、私たちが学んだり開発したりした技術や知識を発信していきたいと思います。どうぞよろしくお願いいたします！

 1.はじめに2023年4月現在、ChatGPTをはじめとしたLLM(Large Language Model, 大規模言語モデル)の発展によって、世界中でAIの研究開発が更なる加速を始めています。この発展の一因には、「Large」の名前が示す通り、AIモデルの大型化による性能向上の発見が挙げられます。
実は機械学習の世界では、モデルを大きくし過ぎると過学習という現象によって性能が低下してしまうことが昔から常識のように考えられていました。ところが近年の深層学習の研究の積み重ねによってこの常識は少しずつ見直されていき、やがてはLLMの成功へと繋がっていきました。
この記事では、過学習とは具体的にどういうことかから説明を始め、現代のLLMに至るまでにどのような研究が進められてきたかの一例を紹介していきます。近年のブームに伴って把握しきれないほど膨大な研究結果が生み出され続けていますし、一方でまだ完全に解明できていないところもいくつもありますが、深層学習研究の歴史の雰囲気が少しでも伝われば幸いです。

 前提知識必要な前提知識は、高校程度の数学・統計レベルに留めたつもりです。
登場する機械学習の用語や概念はほとんど記事内で説明しています。
超最新の専門的な研究については触れていません。
プログラミング言語やライブラリには触れていません。それらの前提知識は不要です。
ただ、全くの未経験よりは、機械学習のサンプルコードを動かしてみたことくらいはある方が理解が早いかもしれません。

 2.過学習とは
 2.1 機械学習の基礎の基礎機械学習とは、コンピュータがデータから何かを学習し、それに基づいて予測や分類を行う技術のことです。この、データから学習を行なったり、未知のデータに対して予測を行ったりするモノ（アルゴリズム・AI・etc）は、機械学習の世界ではモデルとも呼ばれています。
例えば、次のシンプルな例は、二つの数値の関係性を一次式のモデルに学習させたものです。
このデータは人工的に作ったものなので実際には決まっていませんが、例えば、xは何かのプロジェクトの予算金額で、yは売上高かもしれません。または、xは畑に与えた肥料の量で、yはその畑からの作物の収穫量かもしれません。
もし、青丸のデータがたくさんある場合に、xとyの関係性を表すモデル（＝式やアルゴリズム。グラフの赤線）が得られれば、例えば予算xが0.32の時には売上高yはどれくらいになるだろう、または肥料の量xが0.64の時には収穫量yはどれくらいになるだろう、という予測が立てられて便利です。機械学習の典型的な用途の一つは、このように既存のデータ（訓練データ）から入力と出力の関係を学習して、新たな入力に対して出力の予測を立てることです。写真から物体を検出するモデルなら入力は画像で出力は物体の位置や種類になりますし、会話をするモデルなら入力はテキストで出力はそれに対する返答のテキストになります。
予測モデルの構造（＝データの関係に関する仮説）は不都合がない限りどのような形でも構いません。まずはy=ax+bの形の一次式のモデルを採用してみましょう。この場合、データから関係性を学習するということは、既存の訓練データの当てはまりがなるべく良いa, bを探すということに相当します。また、未知のデータに対して予測を立てるということは、予測したいxと学習したa, bからy=ax+bを計算するということに相当します。実際に、ある学習アルゴリズムによって計算された係数を赤い直線でプロットしたものが上の図です。
学習データの各々の(x', y')について、観測値y'と予測値y=ax'+bのズレの大きさを表す数値を誤差または損失と呼びます。ズレの大きさを定義する方法は色々ありますが、いずれの方法でも、ズレが小さくモデルがデータによく当てはまっている時ほど小さな数値になるように定義されます。このモデルについては、RMSE（root mean squared error）という誤差は0.188でした。他方、a=-2, b=2という全然合っていないモデル（すぐ下のグラフ）の場合には、RMSEは1.49になりました。二例だけですが、誤差の大きさと当てはまりの良さに相関関係があることが伺えるかと思います。
一次式に限らず一般的に、学習アルゴリズムによって調整されるモデルの変数はパラメータと呼ばれます。また、モデルに含まれるパラメータの数のことをモデルサイズやモデルの複雑さなどと呼んだりします。
最後に、英語の論文などでは学習（learn）と訓練（train）は別のテクニカルタームとして区別して使われますが、この記事では他の日本語文書の慣習と同様にごっちゃになっています。

 2.2 モデルサイズと過学習の関係性の一例どんな構造のモデルでも、どんな学習アルゴリズムでも、どんな訓練データでも、高性能な＝誤差の小さなモデルが得られるかといえば、もちろんそんなことはありません。
例えば先ほどのグラフをよく見ると、訓練データ（観測データ）は直線ではなくやや下に凸な曲線の上に乗っているように見えます。にも関わらず予測モデルが一次式では、パラメータa, bをどのように調整しても観測値とモデルをピッタリと合わせることはできなさそうです。
それならばと、一次式の代わりに二次式y=ax^2+bx+cのモデルを学習させた結果が次のグラフです。
誤差（RMSE）は0.188から0.107に下がりました。また視覚的にも、一次式より明らかに当てはまりが良くなっているように見えます。
それでは、もっと大きな次数の多項式のモデルを使用してみるのはどうでしょうか？人間がデータの大まかな形を調べてから次数を選ぶのは、不便ですし、データの真のルールの曲線の形によっては視覚的に判断するのが難しかったりします。また、高次の項の係数を0にすれば高次のモデルが低次のモデルを包含して表現できるため、もし低次式の方が当てはまりが良いのであれば、それくらいは学習アルゴリズムにうまいこと調整して貰いたいです。
実際にやってみましょう。例えば30次式で学習した結果は次のようになります。
誤差は0.107から0.046に更に下がりました。しかし、ご覧のとおり学習済みモデルの曲線の形はぐちゃぐちゃです。例えばx=0.3の時に（グラフの描画範囲外ですが）yをマイナスと予測するこのモデルは"正しい"モデルではなさそうに思えます。
このように、古典的なモデルでは、モデルが訓練データに過度に適合してしまうと、予測に使いたい未知の新しいデータに対してうまく汎化できなくなる現象が発生します。これが過学習の一例です。
多項式モデルの次数を増やすということは、一般的な言い方をすると、モデルサイズを増やしたということに相当します。この節では目的変数と従属変数が一つずつの多項式回帰モデルの例を紹介しましたが、他のタスクやアルゴリズムの場合でも、モデルサイズを過度に大きくし過ぎることで過学習が発生する場合があります。
なお、今回の例では学習後の予測モデルをグラフ上にプロットして形を確認しましたが、この方法は一元方程式以外では難しいです。一般的には、手持ちの全データを、モデルを訓練するための訓練データと、モデルの汎化性能を検証するための検証データに分割して、それぞれの損失を比較するという方法で過学習の発生を確認します。30次式の誤差は2次式よりも下がりましたが、これは（訓練データを分けずに全て使った）訓練誤差が小さくなっただけであって、（未知の新しいデータに対する）検証誤差が小さいわけではないことを意味しています。過剰なモデルサイズによる過学習が発生している場合には、訓練誤差と検証誤差とモデルサイズの関係は以下のようなグラフになると考えられています。

 3. Bias-Variance分解とトレードオフ次に、モデルサイズを増加させると何故過学習が生じるのか、という議論においてよくセットで語られるBias-Variance decomposition（バイアス-バリアンス分解）およびBias-Variance tradeoff（バイアス-バリアンス トレードオフ）について説明します。
結論を先に述べると、古典的な機械学習においては、検証誤差をBiasとVarianceという二つの項の和に分解した場合に、モデルサイズに対して二つの項が次のグラフのようにトレードオフ的に変化するために検証誤差全体がU字曲線になる、と考えられていました。
以下の節では、この分解とトレードオフについて詳しく説明していきます。

 3.1 Bias-Variance分解まず、分解は、深層学習も含めて全てのモデルで正しく成立する数学的な理論です。
この記事ではこのページの定義をお借りして説明します。
データの目的変数をy、従属変数をxで表します。xは一般的にはスカラ以外も含まれますが、記述を単純化するために単にxと書きます。
訓練データおよび検証データは分布Pから確率的にサンプリングされるものとします。すなわち(x, y) \sim Pです。

Pからn個のデータセットDをサンプリングすることをD \sim P^nと書きます。

yにはノイズが乗っているものとして、xが与えられた場合のyの期待値を\bar{y}(x)と書きます。これは、例えば教師データの作成において誤りが混入したり、犬か猫か判断が難しい画像にラベルをつけたりする場合などに相当します。
データセットD \sim P^nによって学習されたモデルをh_Dと書きます。Dが確率要素なので、h_Dも確率要素です。
様々なデータセットで学習したモデルの期待値E_{D \sim P^n}[h_D]を\bar{h}と書きます。
このとき、訓練データをランダムにサンプリングして学習した時の検証誤差（MSE）の期待値E_{x, y, D}[(h_D(x)-y)^2]は次のように分解できます。証明はこの記事では省略しますが、詳しく知りたい方は参考元ページをご覧ください。

E_{x, y, D}[(h_D(x)-y)^2] = E_x[(\bar{h}(x) - \bar{y}(x))^2] + E_{x, D}[(h_D(x) - \bar{h}(x))^2] + E_{x, y}[(\bar{y}(x) - y)^2]
第一項E_x[(\bar{h}(x) - \bar{y}(x))^2]はBiasと呼ばれ、予測モデルの期待値が目的変数の期待値とどれだけ近いかを表します。平たく言うと、同じサンプル数のありとあらゆるデータセットをサンプリングして何回も学習したモデルの平均が真の値とどれくらいズレてるかを表します。
第二項E_{x, D}[(h_D(x) - \bar{h}(x))^2]はVarianceと呼ばれ、各々の予測モデルが予測モデルの期待値と比べてどれくらいバラついているかを表しています。言い換えると、同じデータ分布からサンプリングされたものだとしても、使用する訓練データによってどれくらい学習結果がバラつくかの度合いを表しています。
第三項はあまり決まった名前はありませんが、データ固有のノイズ・削減不能なノイズの分散です。
先に述べた通り、この分解は深層学習も含めた任意のモデルのMSEについて成立します。また、ここまでの理論だけでは、モデルの汎化性能についてこれ以上何かが言えるわけではありません。

 3.2 Bias-Varianceトレードオフ目的変数やモデルに具体的な定義を与えない限りはこれ以上議論が進まないため、ここでは前節で説明した多項式モデルを例にバイアスとバリアンスがどうなるかを考えてみましょう。
学習データ(x, y)は人工的に生成したものです。閉区間[0:1]から30点のxをサンプリングして、2次関数2x^2+1に平均0・分散固定のガウスノイズを加えた値がyとなります。この分布が分解の節で説明したPとなり、n=30, \bar{y}(x)=2x^2+1となります。また、ガウスノイズが第三項のデータ固有のノイズ（intrinsic noise）です。
それでは、先にバリアンスの方を見てみましょう。バリアンスの定義はE_{x, D}[(h_D(x) - \bar{h}(x))^2]でした。\bar{h}はひとまず置いておいて、1次式、2次式、30次式モデルのh_D(x)がDのサンプリングによってどれくらいバラつくのかを調べてみました。




1次式、2次式は、そもそも多様な形の曲線を取れないこともあって、異なるDに対しても似たような学習結果になっています。ところが、30次式の場合は、Dが異なれば学習結果も全然別の形になっていることがわかるかと思います。先に述べた通り、バリアンスは同じ分布からサンプリングされたものだとしても、実際に使用する訓練データによって如何に学習結果がバラつくかの度合いとなっています。2次式から30次式の間のh_Dの分散を数値的に計算すれば、この節の冒頭でお見せしたような右肩上がりのバリアンスのグラフが得られるはずです。
次にバイアスの方を見てみます。\bar{h}の定義はE_{D \sim P^n}[h_D]ですが、ありとあらゆるデータセットで期待値を計算することはできないので、近似的に、10万個のDを生成して平均をとってみました。薄い曲線が各々のh_Dで、濃い曲線が10万個のh_Dの標本平均です。
まず、1次式、2次式は次のようになりました。


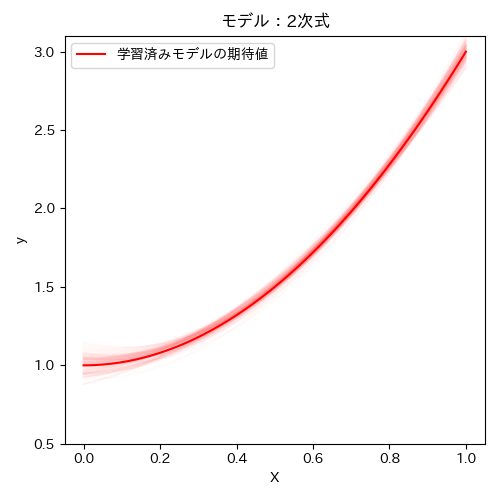
10万全ての学習結果の平均が濃い曲線です。薄い線は最初の100個のデータセットの学習結果を薄く重ねてプロットしたものです。
2次式の方は、\bar{y}(x)=2x^2+1に見事に収束していることがわかると思います。一方、1次式をいくら重ねても\bar{h}（の近似値）も直線的になってしまうようです。この記事の主題とは外れますが、このようにモデルの表現能力が足りないために目的変数をうまく学習できていない状態をunderfitと言ったりします。日本語訳はあまりしっかりと決まっていませんが、未学習や学習不足などです。
なお、30次式の場合はどうなるかというと、実は次のようになりました。
あくまでも\bar{h}の真の定義を計算しているわけではなく、10万個のDによる近似値ですが、h_Dの分散があまりにも大き過ぎて、\bar{y}に収束しませんでした。
ただし、\bar{y}を2次式ではなく高次の式に置き換えて、同じ次数以下のモデルで\bar{h}の近似値を計算すれば、この節の冒頭で紹介したようにバイアスが右肩下がりになったグラフが得られるのではないかと思います。

 4. 深層学習モデルの汎化と性能向上前節では、ある特定のモデル（およびタスク・学習方法）において、モデルサイズを大きくするとバリアンスが増大して過学習が発生する例を紹介しました。それでは、古典的な常識の通り、モデルサイズを変化させた場合のバイアスとバリアンスのU字曲線のトレードオフは、任意のモデル・タスク・学習方法で発生するのでしょうか？
過学習が生じる\Rightarrowバリアンスが高くなる\Rightarrow検証誤差も高くなる、までは一般的に言えそうですが、任意のモデルでモデルサイズを大きくする\Rightarrow過学習が生じる、かどうかはここまでの議論の中では特に何も言及されていません。それどころか実は、すぐ後で紹介するように、深層学習においては反例が見つかっています。
この節では、古典的な常識を打ち破って、LLMが非常に高い性能を叩き出すまでに至った過程の研究の一部を紹介していきます。

 4.1 Double Descentディープニューラルネットワークを用いたモデルでも、多くの場合は多項式の次数のように、一個または数個のハイパーパラメータを変更することで形や大きさを容易に変更することができます。
様々なモデルとデータで研究が進むにつれ、サイズ以外は同種のモデル構造の学習に関して、モデルサイズと検証誤差が以下のような関係になる現象が確認されてきました。これがまさに、検証誤差が単なるU字カーブにはならないという反例の一つです。
このように、検証誤差が始めはU字カーブを描き、ある閾値を超えると再び下がり出す＝すなわち誤差が２回下降する現象はDouble Descentと呼ばれています。
もし閾値よりも右の領域で左のU字領域よりも検証誤差が下がるのであれば、モデルサイズを大きくすればするほど漸近的に性能が改善するという一つの例となります。なお実際には、閾値付近の山が小さくほぼ単調に誤差が減少する場合や、右の領域で左のU字領域の下限よりも高い誤差値に収束してしまう場合など、多様なパターンが確認されています。
Double Descentに関する研究は、何回も学習プログラムを動かして実験的に検証誤差の変化を計測したものもあれば、特定のタスクやモデルに関してモデルサイズと検証誤差の関係式を数学的に証明したものもあります。また、検証誤差だけでなく、バイアス-バリアンス分解についても計測または立式・証明を行った研究も存在します。一例を以下に列挙しました。
Reconciling modern machine learning practice

and the bias-variance trade-of
Two models of double descent for weak features
A Farewell to the Bias-Variance Tradeoff?

An Overview of the Theory of Overparameterized Machine Learning
Memorizing without overfitting: Bias, variance, and interpolation in overparameterized models
なお余談ですが、モデルサイズ以外にも、Double Descentは学習エポック数、訓練データ数、訓練データのラベルノイズなど様々な要因で発生することが知られています。例えば、ハーバード大とOpenAIのメンバー（当時）の論文"Deep Double Descent: Where Bigger Models and More Data Hurt"に様々な事例がまとめられています。以下のページなどでこの論文の日本語解説も読むことができます。
https://www.acceluniverse.com/blog/developers/2020/01/deep-double-descent-where-bigger-models-and-more-data-hurt.html
https://zenn.dev/hnishi/articles/20201015-deep-double-descent

 4.2 正則化それでは何故（Double Descentに限らず）大きな深層学習モデルで過学習が発生しないかというと、正則化が働いて表現能力を自動調整しているからだという仮説があります。
例えば、書籍「ディープラーニングを支える技術２」では、以下のように述べられています。
（前略）

ニューラルネットワークはモデルの表現力を必要最小限に抑えるしくみが備わっていたためです。

あらかじめ大きめの表現力を持ったモデルを使っておき、問題に応じてこの表現力を適切なサイズまで自動的に小さくしていっているとみなせます。
また東大の鈴木先生のスライドでも、（深層学習モデルでは）
見かけの大きさ (パラメータ数) よりも実質的な大きさ (自由度) はかなり小さいはず．
という仮説について説明されています。
正則化とは、何らかの方法で過度に複雑なパラメータが得られないようにするための手法や仕組みのことです。これ自体は深層学習のブームより以前に考案されたもので、広く知られていました。例えば、L2正則化（リッジ回帰）という方法を用いて30次式モデルを学習すると、実は過学習は起こらずに以下のような結果になります。
L1正則化、L2正則化、early stoppingなどの正則化手法は深層学習以外の機械学習モデル・手法でも幅広く使用することができます。また近年の人気の機械学習ライブラリでは、一部の正則化手法がデフォルトで使用されるようになっています。言い換えると、エンドユーザが何もしなくても既に学習が正則化され、過学習がある程度抑制されているのです。
ニューラルネットワークに固有の正則化手法としては、ドロップアウトというものが有名です。これは、（ここまでニューラルネットワークの内部構造に一切触れてこなかったので説明が難しいですが）学習時にニューロンをランダムに不活性化することによって、アンサンブル学習と呼ばれる手法に似た効果を生じる方法です。
しかし実は、前の節で述べた論文の一つDeep Double Descent: Where Bigger Models and More Data Hurtでは、正則化手法を使っていないのにDouble Descentが生じたという旨が記載されています。また、次の節で詳しく紹介するLLMに関するOpenAIの論文でも、正則化は明示的に調整していない旨が記載されています。
どうやらニューラルネットワークは、その構造自体が何かしらの陰的正則化機能を含んでいるとの説があります。非常に高度な数学理論を駆使してようやく一部が解き明かされつつあるような状況のようですので、この記事で説明するのは難しいですが、先に挙げた書籍やスライドなどにもう少しだけ説明が載っていますので興味のある方はそちらをご覧ください。

 4.3 Neural Scaling Laws厳密で詳細な理屈はさておき、深層学習においては（実験した範囲では）モデルサイズを大きくするほど汎化性能が向上するという現象がいくつも確認されています。
GPTのOpenAIを始めとして、大規模モデルを研究してきた研究者・組織は、ニューラルネットワークのモデルサイズや訓練データ量とモデルの（汎化）性能の関係は冪乗則に支配されていると主張されています。
例えば論文"Scaling Laws for Neural Language Models"では、ある種の深層学習モデルのパラメータ数Nとクロスエントロピー検証誤差L(N)の関係が報告されています。幾つかのバリエーションがありますが、例えば、データ量が十分大きい場合、自己回帰モデルとして学習されたTransformerについて、NとL(N)は（数多くの実験を繰り返して調べた範囲においては）

L(N)=(N_c/N)^{\alpha_N}; \alpha_N \approx 0.076, N_c \approx 8.8^{13}
という関係があったとのことです。この式を片対数グラフにプロットすると下記のようになります。
TransformerやLSTMなど、複数のモデルで同様の実験を行なっても、指数の大きさは違えど同様の冪乗則が確認されています。この論文は2020年1月発表で、GPT-2と同様の15億のパラメータ数までが調査されています。この論文では他にも、大きなモデルの方が、少ないデータサンプル数の学習で同程度の性能に到達する例などを紹介しています。
他にも、GPT-3の論文"Language Models are Few-Shot Learners"においても、モデルサイズとベンチマークタスクの損失の関係性が報告されています。最大1750億パラメータのGPT-3でも同様の冪乗則が確認されたようです。

 5. 終わりに2023年4月現在、AI研究は更なる加速を見せています。
OpenAIは今後は情報を非公開にしていく方針のようですが、同規模のLLMを自分達で開発しようと試みる組織が増えていますので、更にモデルサイズを増加させたら一体どうなっていくのか、近い将来にわかるのではないでしょうか。
一方で、現段階のLLMでもかなりのハードウェアリソースが要求されている上、モデルサイズの増加に伴って学習に必要なリソースも冪乗で増えてしまいますので、モデルサイズのスケーリングの意味での競争は今後減速していくのではないかという声も聞こえてきます。また、OpenAIの現CEOアルトマン氏は「巨大なモデルを用いる時代は終わりつつあると思います」と語ったらしいです（筆者は一次ソースは追えてないですが）。
またこれまでの歴史を振り返ると、モデルの大規模化による性能向上が進むたびに、なるべく少ない計算リソースやモデルパラメータで同等の性能を目指す試みが繰り返されています。少し前の話ですが、例えば、2018年に発表されたBERTという言語モデルに対して、2019年にはALBERTなどといった軽量モデルが開発されています。SNSやGitHubなどでは、ChatGPTやGPT4の発表を受けての軽量化の試みがすでに広がっています。
正則化の節で紹介した通り、大規模モデルでも実質的なパラメータの数は見かけのモデルサイズよりは小さいらしく、実際、学習されたパラメータの中身を見てみると、使われていなかったり冗長だったりするパラメータがあるらしいことは既に知られています。特に、学習前にランダムに初期されたパラメータのうち、一部分のみが最終的な性能に寄与するという宝くじ仮説という学説も研究が進んでいます。相対的に小さなモデルでも最大の大規模モデルと同程度の性能を達成できる可能性もまだまだあるのではないでしょうか。ただし、最終的に使われるのは一部だとしても、ランダムなパラメータの中の当たりクジが増えるため大きいモデルの方が汎化しやすくなると、前述の書籍などでは説明されています。当たりくじの存在が最終的な性能に対して支配的な要因だとすると、モデルのサイズを増やさずに当たりくじを得るためには何らかの工夫が必要になりそうです。
最終的にはどんな未来に辿り着くのか、今から待ち遠しいです。今後の研究動向や関連研究についてもブログ記事で紹介していきたいと思います。