これならわかるSelf-Attention
この記事では、BERTやGPTなどのAIモデルで使用されているSelf-Attentionネットワークについて説明します。
TransformerやEncoder層・Decoder層、Transformer以外のAttentionの説明などは一切省略し、Self-Attentionにだけフォーカスしました。その代わり、Self-Attentionについては「完全に理解した」と感じてもらえるように頑張って解説していきます。
なお、同一の名称でマイナーチェンジされた他のネットワークがあるかもしれませんが、本稿で説明する各種Attentionネットワークは全てAll You Need Is Attentionで定義されているものを指します。
全体像
- Self-AttentionはMulti-Head Attentionというネットワークの特殊化です。
- Multi-Head AttentionはScaled Dot-Product Attentionというネットワークの拡張です。
- また、様々な記事で単語同士の関連性が云々などと解説されているのは、実はScaled Dot-Product Attention自体の仕組みや機能の部分です。
- よって、Scaled Dot-Product Attentionを把握できれば、Self-Attentionの気持ちは大体理解できるはずです。Multi-Head AttentionやSelf-Attentionに至る拡張や特殊化は、その後に理解していきましょう。
Scaled Dot-Product Attention
一言で述べると、Scaled Dot-Product Attentionは、KeyベクトルとValueベクトルのペアからなる辞書に対して、Valueベクトルの加重平均を計算するネットワークです。加重平均は、Queryベクトル1つごとに、QueryにマッチするKeyのValueほど大きな重みを持つように計算します。
しかし、いきなりそのように述べられても何が何だかわからないと思いますので、少しずつ噛み砕いて説明していきます。
最初に最低限の構造を頭に入れる
Scaled Dot-Product Attentionは、実は学習用のパラメータを持たない、入力された行列同士を単に演算するだけのネットワークです。
ミニバッチまで考慮すると入力は階数3のテンソルですが、多くの解説記事と同様に、1サンプル分の行列を入力として説明していきます。また、理解を助けるために、以下では「行列」の代わりに「ベクトルの配列」という表現を用いる場合があります。1つの行が(横)ベクトルで、1行目2行目……がそれぞれ1ベクトル目2ベクトル目です。
さて、具体的には、Scaled Dot-Product Attentionは、
-
Q d_Q N -
K d_K M -
V d_V M - 出力は、長さ
d_V N - ベクトルの長さは
d_Q=d_K
計算の気持ちを理解するにはまずは最低限これだけ覚えれば十分です。

計算の気持ちを理解する
Scaled Dot-Product Attentionが何を計算しているかをざっくりと表すと、以下のようになります。なお、多くの解説記事では単語の埋め込み表現ベクトルを用いた例がほとんどですが、より気持ちが分かりやすいと思われる別の例で説明します。
KeyとValueの気持ち
まず、KeyとValueは、実数ベクトル型に限定されてはいますが、IT全般でよく使われる辞書データそのものです。
出力行列の気持ち
Scaled Dot-Product Attentionの出力は、Queryベクトル一つずつごとに、Value行列の各ベクトルを加重平均したベクトルの配列です。これは、Queryすなわち「質問」によってKeyベクトルの配列を柔らかくフィルタリングするイメージです。出力のサイズは長さ
重みの計算の気持ち
加重平均の重み
- ベクトルの配列からなる行列
Q, K Q K^{\mathrm{T}} i,j Q i K j -
\text{softmax}
これらをまとめて、QueryベクトルとKeyベクトルのドット積(dot product)が大きいほど重みも大きくなることだけわかれば十分です。
ドット積が大きいほど重みが大きくなるということは、ドット積の定義より
- ノルムの大きいKeyベクトルほど重みが大きくなる。
- QueryベクトルとKeyベクトルのなす角が小さいほど重みは大きくなる。
ということです。直観的にはQueryベクトルに似たKeyベクトルほど大きい重みを持つと考えられますが、コサイン類似度とは異なり、ベクトルの方向だけでなく大きさにも影響されることに注意してください。
なお、ノルムの大きいQueryベクトルでもドット積は大きくなりますが、全てのKeyベクトルとのドット積に同じノルムが掛けられるため、Queryベクトルが大きいほど、
Scaled Dot-Product Attention全体の計算式は
ネットワーク
参考までに、Scaled Dot-Product Attentionのネットワークを図で示すと以下のようになります。
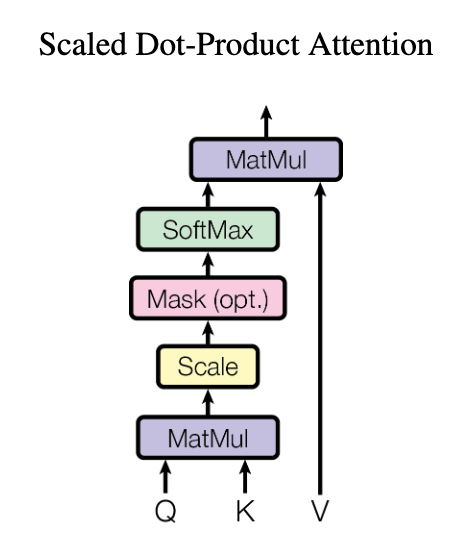
All You Need Is Attention, P.4, Figure 2 left
MaskはTransformerの学習時に使用されますが、Scaled Dot-Product Attention単体には直接関係ないため、本稿では解説しません。
Multi-Head Attention
Multi-Head AttentionはScaled Dot-Product Attentionを複数個重ねたネットワークです。まずは図で見てもらうのが良いでしょう。
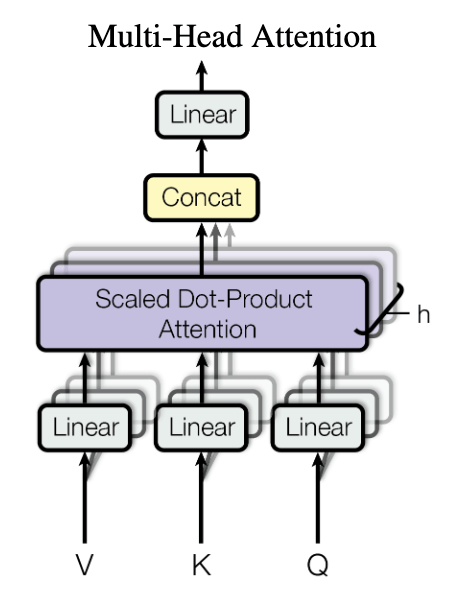
All You Need Is Attention, P.4, Figure 2 right
各Scaled Dot-Product Attention(またはその手前の線形変換層を含めて?)はHeadと呼ばれています。これが複数あるため「Multi-Head」Attentionです。
各Scaled Dot-Product Attentionへの入力行列は、Multi-Head Attentionへの入力行列
各Headの最初の線形変換でMulti-Head Attention全体への入力からそのHeadが着目している関係性の成分を抽出し、Headごとに別々のAttention Matrixを計算することで、Multi-Head Attentionは複雑な性質を持つデータをうまく処理しているものと考えることができます。
何を意味しているかを読み取るのは難しいですが、実際に言語で訓練したネットワークについて、同一の入力に対して二つのHeadのAttention Matrixが異なる注目をしていることを確認した例があります。
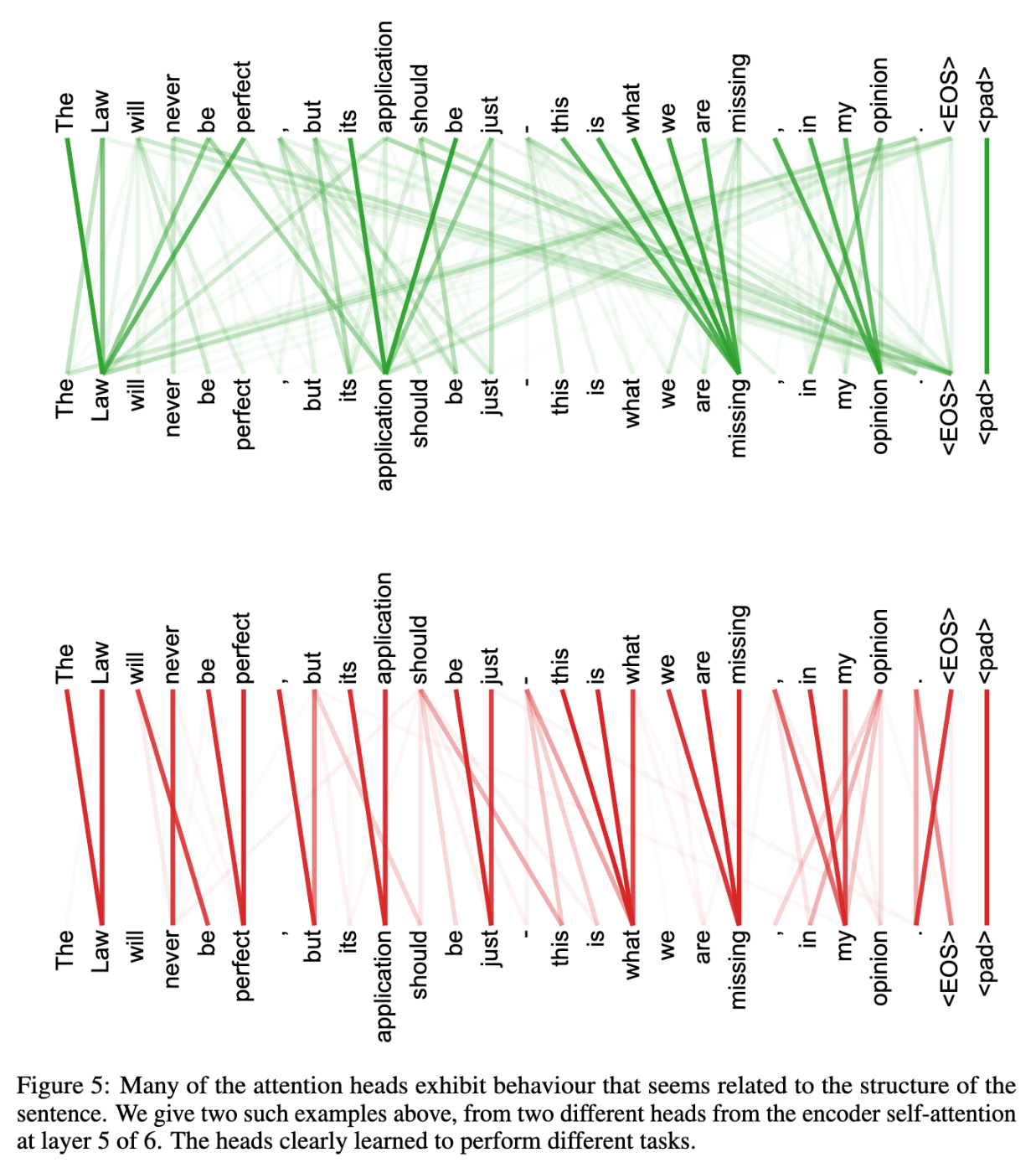
All You Need Is Attention, P.15, Figure 5
ただし、複数のHeadは、異なる関係性を捉える余地・可能性を生み出しているだけであり、この構造であればいかなる場合にも異なる関係性を学習するわけではない、ということに注意してください。多チャネルのConvolutionなどでも同様ですが、実際に訓練を行うと各Headがほぼ同じ重みを学習することもあります。損失関数などを工夫することで、学習パラメータの多様性を促進する仕組みなども研究されているようです。
最後に、各Headの出力はConcatつまり単純に重ねられた後に線形変換されて出力されます。
Self-Attention
ここまでしっかりと理解できれば後は簡単です。Self-Attentionは、単一の行列を入力として、
ちなみに、Self-Attentionにおいても、各HeadのAttention Matrixは一般的には非対称行列です。大元の入力行列は同じでも、各HeadでScaled Dot-Product Attentionを実行する前に、
Transformer全体が何を計算しているのかを解釈するのは更に難しいですが、ひとまず単一のSelf-Attentionが何を計算しているのかはこのようなイメージです。
サイズパラメータについて
Self-Attention単体の解説としてはこのくらいですが、これをTransformer内で重ねて使うためには、特にサイズ周りのパラメータについて、いくつかのコツあるいは必要条件があります。
- 同一のサイズでなければいけない制約
- 勾配発散を防ぐためのスケーリング
- ドット積の次元の呪いの防止、etc
拙著ではありませんが、例えば次の記事などで詳しく解説されていますのでご興味があれば参考にしてみてください。
終わりに
以上、Scaled Dot-Product AttentionからSelf-Attentionに至るまでの計算の気持ちを説明しました。読者の皆様のお役に立てたのであれば幸いです。
なお、株式会社Knowhereでは、技術の力を利用して「誰もがスポーツが上手くなれる環境を」をミッションに活動しています。現在はNLPよりもCVが主なターゲットですが、TransformerもCVにも応用されていますし、このような先端技術の力を活かして製品開発を行うメンバーを募集中です。ご興味のある方はご連絡をいただければ嬉しいです。
Discussion