【勉強】GLM（一般化線形モデル）とGAM（一般化加法モデル）

前提

以下について理解する

• GLM（General Linear Model）: 一般線形モデル
• GLM (Generalized Linear Model) : 一般化線形モデル
• GAM (Generalized Additive Model) : 一般化加法モデル
• GA2M : 2019 年に Microsoft が出した GAM の進化形

疑問

• 一般線形モデルと一般化線形モデルの違い？
• GLM と GAM と GA2M のそれぞれの特徴？
• python を用いて、どうモデル化するのか？
• どういうデータセットや問題設定に向いているのか？
• 状態空間モデルとの関係は？

参考

• 一般化線形モデル (GLM) & 一般化加法モデル(GAM)
• pga-tour-analysis-by-gam | Kaggle
• 一般化加法モデルと格付表 l DataRobot

To-dos

• Linear Regresssion
• Poisson Regression
• [ing] Logistic Regression
• 一般化線形モデル
• 一般化加法モデル
• GA2M

Linear Regression（線形回帰）

• 一般線形モデルの例に Linear Regression（線形回帰） がある
• Linear Regression は応答変数$y$が、説明変数$x$の線形和と正規分布に従う誤差項$ε$で表されると仮定する

$$ε \sim Norm(0, σ)$$

$$y = w_1x_1 + w_2x_2 + ... w_nx_n + ε$$

• $y$は以下のような正規分布に従っているとも見れる

$$y \sim Norm(w_1x_1 + ... + w_nx_n, σ)$$

• Linear Regression は、 以下 2 つを仮定していると言える
  • $y$が正規分布になること
  • その期待値は、説明変数$x$の重み付き線形和で説明できる
• 違う見方をしてみる
  • y のうち、説明可能な部分は x の線形和で表現できるはずだ
  • 説明できない部分は誤差とみなし、それは正規分布に従うはずだ

コード

linear.py

# 一般線形モデルのプロット
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

# サンプルデータ生成
np.random.seed(0)
X = np.linspace(-10, 10, 100)
y = 3 * X + 5 + np.random.normal(0, 5, size=len(X))

# 線形回帰モデルの適用
coefficients = np.polyfit(X, y, 1)
polynomial = np.poly1d(coefficients)
y_fit = polynomial(X)

# xの値を-10から10まで2.5刻みで選ぶ
x_values_for_normal = np.arange(-10, 10.1, 2.5)

# 正規分布のパラメータ（仮に標準偏差を5とする）
std_dev = 5

# 既存のデータと線形回帰をプロット
plt.scatter(X, y, label='Actual Data', alpha=0.5)
plt.plot(X, y_fit, label='Linear Regression (Example of GLM)', color='red')

# 各xにおける正規分布をプロット
for x_val in x_values_for_normal:
    mean_y_at_x = polynomial(x_val)
    y_normal = np.linspace(mean_y_at_x - 3*std_dev, mean_y_at_x + 3*std_dev, 100)
    x_normal = norm.pdf(y_normal, mean_y_at_x, std_dev)
    plt.plot(x_val + x_normal * 4, y_normal, color='green')

plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Example of Generalized Linear Model (GLM): Linear Regression')
plt.grid(True)
plt.show()

ロジスティック回帰(wip)

• カテゴリカルな目的変数（例: 雨・くもり・晴れ）と 1 つ以上の説明変数との関係をモデリングする回帰分析の 1 種

$$P(Y=k) = \frac{1}{1 + \exp(-(w_1x_1 + ... w_nx_n + b))}$$

ポアソン回帰

ポアソン回帰に行く前に、まずはポアソン分布の復習

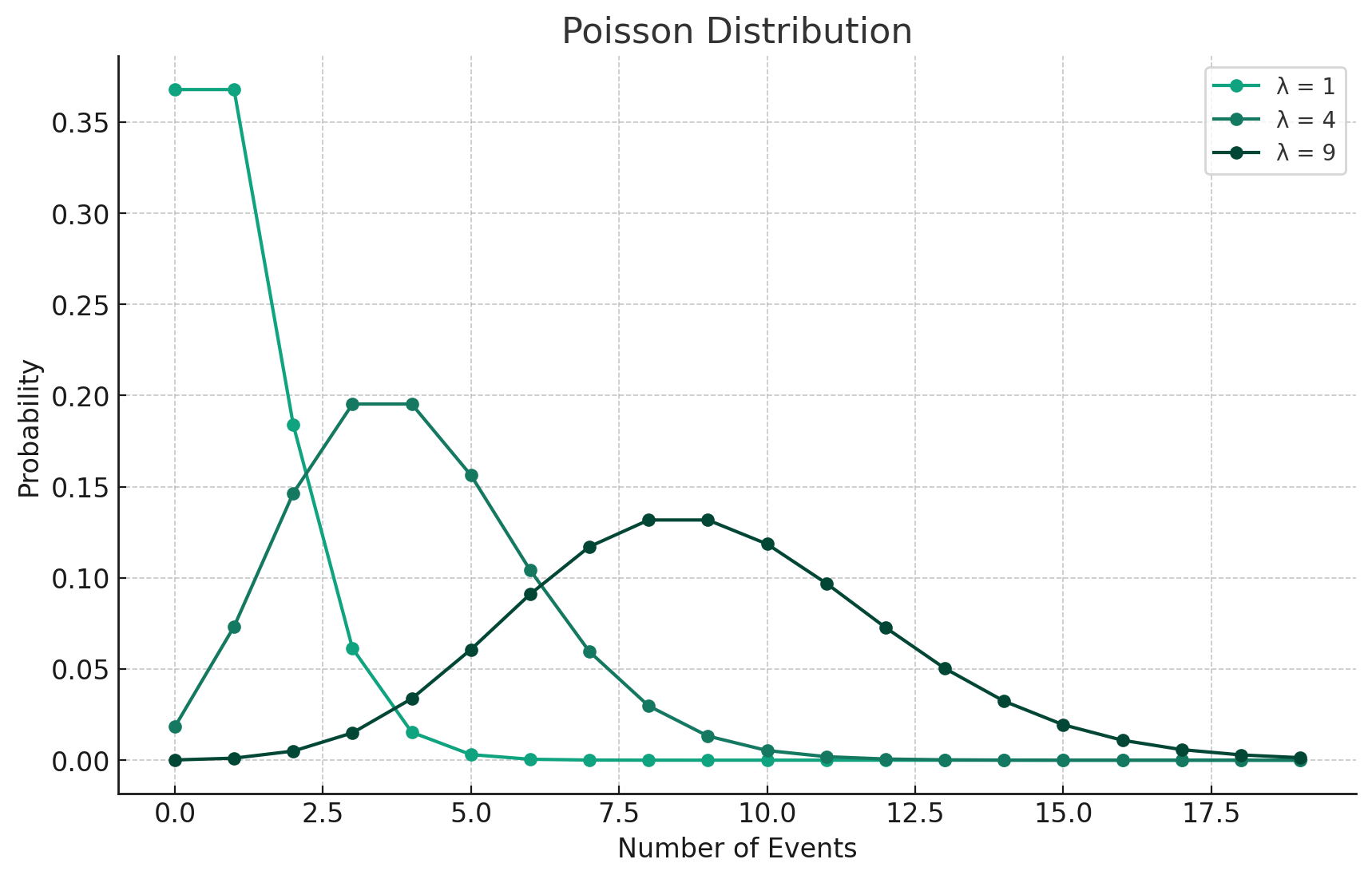
ポアソン分布

• ある期間に平均 λ 回起こる現象における、発生回数$X$が従う分布のこと

$$P(X=k) = \frac{e^{-λ}λ^k}{k!}$$

• ポアソン分布の平均は$λ$、分散は$\sqrtλ$である
• ポアソン分布の例: コイントス
  • 確率$p$で表になるコインを$n$回トスする施行を何度も実施する
  • このとき、各施行で表になった回数の頻度分布は$λ=np$のポアソン分布になる
• ポアソン分布の形は、$λ$が発生回数（≒ 発生確率）だと意識すれば想像しやすい
  • $λ$が小さければ、確率が低いので発生回数 0 が多くなるから、左に山があり、右にロングテールが続く分布になる
  • $λ$が大きくなればなるほど、山の位置が右に移動し、裾野も広がっていく

コード

poisson_plot.py

# ポアソン分布のプロット
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import poisson

# パラメータ（平均発生率）
lambdas = [1, 4, 9]

# データポイント
x = np.arange(0, 20)

# プロット
plt.figure(figsize=(10, 6))
for lam in lambdas:
    y = poisson.pmf(x, lam)
    plt.plot(x, y, marker='o', label=f'λ = {lam}')

plt.title('Poisson Distribution')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()

二項分布との関係

• WIP

ポアソン回帰

• ポアソン回帰は、応答変数$y$が平均$λ$のポアソン分布に従うと仮定し、この$λ$を説明変数$x$を用いて回帰する手法
  • 以下のように、$λ$自体をモデリングする。

$$y \sim Poisson(λ)$$

$$λ = \exp(w_1x_1 + w_2x_2 + ... w_nx_n)$$

• つまり、ポアソン回帰を実施するとは以下のような仮定をおいている
  • $y$はコイントスのような独立事象を複数回施行した際の発生回数のようなもの
    • ＝ 平均して$λ$回発生する。ゆらぎがあり、それは$\sqrtλ$である
  • $λ$ は説明変数の線形和で説明可能

コード

poisson_regression.py

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import PoissonRegressor
from scipy.stats import poisson

# ポアソン分布からサンプルデータを生成
np.random.seed(0)
X_poisson = np.linspace(-10, 10, 100).reshape(-1, 1)
lambda_poisson = np.exp(0.5 * X_poisson + 3)  # λ = exp(0.5 * X + 3)
y_poisson = np.random.poisson(lambda_poisson)

# Poisson回帰モデルを適用
poisson_reg = PoissonRegressor()
poisson_reg.fit(X_poisson, y_poisson.ravel())
y_fit_poisson = poisson_reg.predict(X_poisson)

# 既存のデータとポアソン回帰をプロット
plt.scatter(X_poisson, y_poisson, label="Actual Data", alpha=0.5, color="blue")
plt.plot(X_poisson, y_fit_poisson, label="Poisson Regression", color="red")

# 各xにおけるポアソン分布をプロット（2.5刻み）
for x_val in np.arange(-10, 10.1, 2.5):
    print(x_val)
    a = poisson_reg.coef_
    b = poisson_reg.intercept_
    mean_y_at_x = np.exp(a * x_val + b)
    # 0~3λまでのポアソン分布の値を得る
    inputs = np.arange(0, max(10, int(mean_y_at_x * 3)))
    outputs = poisson.pmf(inputs, mean_y_at_x)
    max_output = max(outputs)
    outputs = outputs / max_output * (2.5 / 2)
    # x,y反転している
    plt.scatter(outputs + x_val, inputs, c="green", s=outputs)

plt.xlabel("X")
plt.ylabel("y")
plt.legend()
plt.title("Example of Poisson Regression")
plt.grid(True)
plt.xlim(-10, 12)
plt.ylim(-100, 3100)
plt.show()

一般化線形モデル

一般化線形モデルとは、以下を仮定する統計モデルのこと。

• (1) 期待値が「線形予測子」の線形関数で表され、
• (2) 誤差が「指数型分布族の分布」に独立に従う

(1)を数式で表すと以下になる
$$ g(E[y]) = w_0 + w_1x_1 + w_2x_2 + ... w_nx_n $$

一般化線形混合モデル

階層ベイズモデル

一般化加法モデル