Zenn
👙

セクシー女優の顔特徴量をUMAPで次元削減、クラスタリングしてみた

2022/02/16に公開
Python
ディープラーニング
機械学習
#
computervision
#
umap
tech

目次

  1. 画像からセクシー女優を検索するツールを実装してみた
  2. セクシー女優の顔特徴量をUMAPで次元削減、クラスタリングしてみた（本記事）

はじめに

前回の記事『画像からセクシー女優を検索するツールを実装してみた』では、InsightFaceを使い、画像から顔検出、顔認証を行って、類似するセクシー女優を検索できるようにしてみました。

今回はその顔特徴量データ（1,000人、5,000枚分）を使って、次元削減、クラスタリングの実験をしてみました。

実験はGoogle Colaboratory上で行いました。ノートブックは以下の通りです。
今回、初めてGoogle Colaboratoryを使いました。とても便利ですね。

https://colab.research.google.com/drive/1Cd8WyLDJB_EHSh1m5kKOrNV9TQWKBZst?usp=sharing

何のために次元削減、クラスタリングするの？

今回使用した顔特徴量のデータは、512次元で構成されています。
「異常な（他人の）顔特徴量が含まれていないか？」、「誰と誰が似ているか？」といった分析を行いたいのですが、次元数が高いと直感的に取り扱うのが難しいので、3次元、2次元などの低次元で表現できると便利です。

ただ、今回は「UMAPを使ってみる」のが目的だったので、実は上記の目的は後付けだったりします。

何を使うの？UMAPとは？

「次元削減」と聞くと、t-SNEを思い浮かべる方が多いかと思います。と言うか、私がそうでした。
そんな中、つい最近、「UMAP」というアルゴリズムと、それを実装したライブラリの存在を知りました。

t-SNEと比べてUMAPの利点は、

  • 結果が安定している（再実行しても近しい結果を得られる）
  • 新たなデータも写像できる（fitとtransformを別々に実行できる）
  • 逆写像できる（元の次元に戻せる）

などがあります。詳しくは公式ドキュメントを参照ください。

インストール

UMAPは、pipコマンドで簡単にインストールすることができます。

pip install umap-learn

具体例

UMAPは、「教師あり」と「教師なし」の次元削減、クラスタリングの両方を行うことができます。

以下に具体的な例を示します。

データの取得

まずは、顔特徴量データを取得します。wgetを使う例を示します。

wget https://github.com/kleamp1e/pornstar-recognizer/raw/main/backend/db/actor.npy

actor.npyには、女優ID、顔特徴量のベクトル（512次元）が1,000人、5,000枚分含まれています。

actors = np.load("actor.npy")
actors.dtype #=> dtype([('id', '<u2'), ('embedding', '<f2', (512,))])
actors.shape #=> (5000,)

色の生成

本筋からはずれますが、可視化のために女優IDに対応する色を事前に生成しています。HSV色空間の良い感じの領域からランダムにサンプリングしています。

def make_random_colors(n_colors):
    h = np.random.rand(n_colors)
    s = np.random.rand(n_colors) * 0.6 + 0.4
    v = np.random.rand(n_colors) * 0.6 + 0.3
    rgb = [colorsys.hsv_to_rgb(h, s, v) for h, s, v in zip(h, s, v)]
    return rgb

def draw_colors(colors, cell_dx=10, cell_dy=10, background=(128, 128, 128)):
    cells = len(colors)
    cell_nx = math.ceil(math.sqrt(cells))
    image_dx = cell_nx * cell_dx
    image_dy = math.ceil(cells / cell_nx) * cell_dy
    image = Image.new("RGB", (image_dx, image_dy), background)
    draw = ImageDraw.Draw(image)
    for index, (r, g, b) in enumerate(colors):
        x = index % cell_nx
        y = index // cell_nx
        draw.rectangle(
            (x * cell_dx, y * cell_dy, (x + 1) * cell_dx, (y + 1) * cell_dy),
            fill=(int(r * 255), int(g * 255), int(b * 255)))
    return image

n_colors = len(np.unique(actors["id"]))
n_colors #=> 1000

np.random.seed(42)
colors = make_random_colors(n_colors)
draw_colors(colors)

可視化した結果は、以下の通りです。

教師ありで次元削減、クラスタリング

まずは、教師ありで次元削減、クラスタリングしてみます。ここでの教師データは女優IDです。

削減後の次元数（n_components）には2、距離の指標にはコサイン類似度（cosine）を指定しています。

reducer = umap.UMAP(n_components=2, metric="cosine")
reduced_embedding = reducer.fit_transform(actors["embedding"], actors["id"])
reduced_embedding.shape #=> (5000, 2)

plt.figure(figsize=(10, 10))
plt.scatter(
    reduced_embedding[:, 0],
    reduced_embedding[:, 1],
    c=[colors[id] for id in actors["id"]],
    marker="+")

可視化した結果は、以下の通りです。

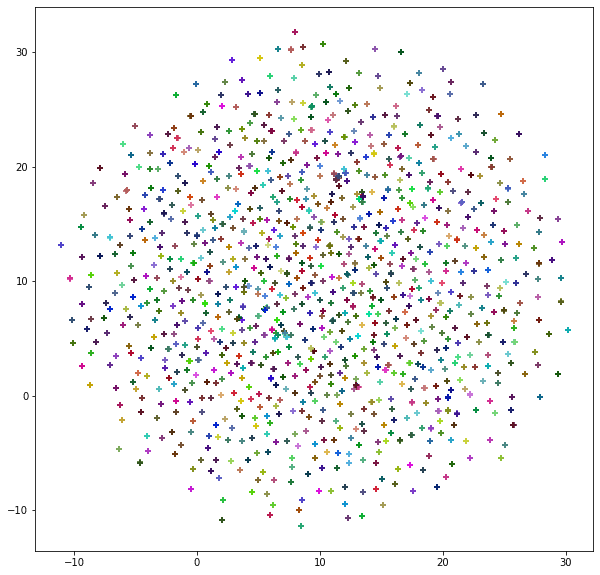
所々、ギュッと固まっている箇所がありますが、全体的にはばらけているように見えます。
また、それぞれの女優IDに5枚分の顔特徴量がありますが、重なって1つの点に見えます。

教師なしで次元削減、クラスタリング

こちらが本筋ですが、教師なしで次元削減、クラスタリングしてみます。fit_transformに第2引数を与えないことで、教師なしモードで動きます。

reducer = umap.UMAP(n_components=2, metric="cosine")
reduced_embedding = reducer.fit_transform(actors["embedding"])
reduced_embedding.shape #=> (5000, 2)

plt.figure(figsize=(10, 10))
plt.scatter(
    reduced_embedding[:, 0],
    reduced_embedding[:, 1],
    c=[colors[id] for id in actors["id"]],
    marker="+")

可視化した結果は、以下の通りです。

さすがに教師なしでは女優ID毎の凝集度は低めです。それでも同じ女優IDは顔特徴量は近くにプロットされているように見えます。

1,000人分をプロットすると区別が難しいので、先頭5人分の顔特徴量だけに色を付けてみます。

plt.figure(figsize=(10, 10))
plt.scatter(
    reduced_embedding[:, 0],
    reduced_embedding[:, 1],
    color=(0.8, 0.8, 0.8),
    marker="+")
for id in np.unique(actors["id"]):
    if 0 <= id <= 4:
        selector = (actors["id"] == id)
        plt.scatter(
            reduced_embedding[:, 0][selector],
            reduced_embedding[:, 1][selector],
            c=[colors[id] for _ in range(np.sum(selector))],
            label=str(id),
            marker="+")
plt.legend()

可視化した結果は、以下の通りです。

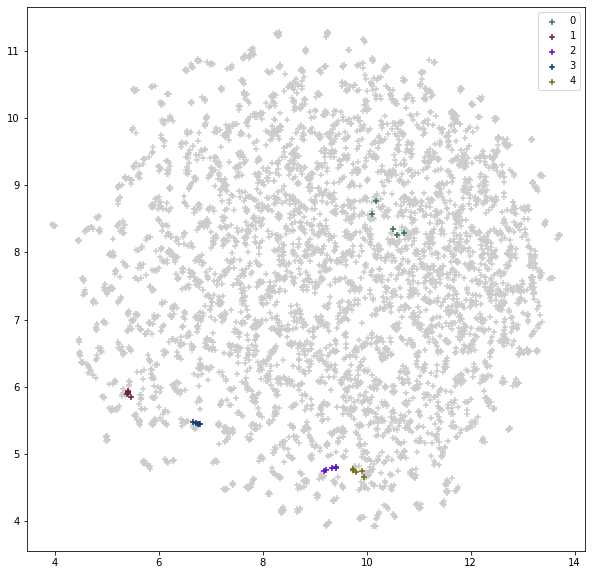
女優ID 0だけは凝集度が低めですが、他の女優IDについては凝集しているように見えます。

逆写像

Google Colaboratoryノートブックには含まれていませんが、2次元→512次元の逆写像も実験してみました。inverse_transform関数を使うことで簡単に逆写像できますが、この処理はまあまあ重めで時間が掛かります。

残念ながらこちらは上手く行かず、「512次元→2次元→512次元」のように「写像→逆写像」して類似度を計算してみましたが、とても低い類似度になりました。

上記のような散布図の任意の点を選択し、その点に近い女優を検索する・・・ということをやりたかったのですが、UMAPでは難しそうです。

最後に

UMAPを使うことで、512次元を良い感じに次元削減、クラスタリングすることができました。
今後、データの探索、可視化などに活かしていきたいと思います。

Discussion