私が感動した Processing 製の作品のソースコードを解析してみた
こんにちは.株式会社ゆめみの Keeth こと桑原です.Twitter には #つぶやきProcessing という魅力的なタグがあり,毎日数々の美しい作品がこのタグを付けて投稿されています.これを眺めるだけでも一日中過ごせるくらいです(個人の感覚です).
今日はその中でも特に度肝を抜かれ,かつ感動した作品が 2022/11/04 に投稿されておりましたので,個人の拙い能力で解析に挑戦してみました 💁
※一部解析しきれていない部分がありますが,ご容赦いただけますと幸いです…何分勉強中の者でして…
作品
なにはともあれ今回対象の作品.
初めてみたときは思わず言葉を失いました.いや,これ twitter のツイートですのでかなり文字数も少ないんですよ!なのにこの表現ってどうなってんの!?と…
これはかなり学びになると思い解析を試みようと思い立った次第です.それにしても美しい…
ソースコード
では上記ツイートのコードを改めて書きます.
$=[]
draw=_=>{$[0]??createCanvas(540,540);background(0,9);$=$.map((v,i)=>stroke(i,i/3,i/5).point(v.copy().add(2,1.6).mult(135))+v.add(sin(v.y*(r=(v.x*2+2.5^v.y+2)*8))/90,cos(v.x*r)/90))[2e3]?$.slice(-1980):[...$,...[...Array(20)].map(p5.Vector.random3D)]}
まぁ,minify されているので見辛いですよね 😅 ということで整形しました.
$ = [];
draw = (_) => {
$[0] ?? createCanvas(540, 540);
background(0, 9);
$ = $.map(
(v, i) =>
stroke(i, i / 3, i / 5).point(v.copy().add(2, 1.6).mult(135)) +
v.add(
sin(v.y * (r = ((v.x * 2 + 2.5) ^ (v.y + 2)) * 8)) / 90,
cos(v.x * r) / 90,
),
)[2e3]
? $.slice(-1980)
: [...$, ...[...Array(20)].map(p5.Vector.random3D)];
};
これでも良いですが,もっと分かりやすいコードを @youtoy さんが Qiita で書かれていました ので,コードをお借りしました 💁(微調整はしています)
let $ = [];
const num = 2e3;
function setup() {
createCanvas(600, 600);
}
function draw() {
background(0, 9);
const arr = $.map((v, i) => {
stroke(i, i / 3, i / 5);
point(v.copy().add(2, 1.6).mult(135));
r = ((v.x * 2 + 2.5) ^ (v.y + 2)) * 8;
return v.add(sin(v.y * r) / 90, cos(v.x * r) / 90);
});
if (arr[num]) {
$ = $.slice(-(num - 20));
} else {
let newArr = [];
for (let i = 0; i < 20; i++) {
newArr.push(p5.Vector.random3D());
}
$ = [...$, ...newArr];
}
}
本記事では基本的にこちらのバージョンを用いて解説しますー(*・ω・)ノ
解析ポイント
計算処理もそうですが,今回は
- ベクトルを使って表現されていること
- 円の表現の工夫
の2点が重要だなと感じました.その辺りを意識して色々分析したものを書いていきます.
① p5.Vector.random3D
まずは大元となるベクトルのインスタンスの生成に使われているこちらのメソッド.単にベクトルのインスタンスを生成したいのであれば createVector() でも良かったのですが,どうも 円の表現 に絡んでいるのはここだろうなと感じておりまして.
試しに以下のように途中処理を排除して何が描かれるか見てみました 💁
const arr = $.map((v, i) => {
stroke(i, i / 3, i / 5);
// 後述しますが,ここはプロットの位置調整のみで
// 処理自体には影響はありません
point(v.copy().add(2, 1.6).mult(135));
// r = ((v.x * 2 + 2.5) ^ (v.y + 2)) * 8;
r = 1;
//return v.add(sin(v.y * r) / 12, cos(v.x * r) / 12);
return v;
});
if (arr[num]) {
$ = $.slice(-(num - 20));
} else {
let newArr = [];
for (let i = 0; i < 20; i++) {
newArr.push(p5.Vector.random3D());
}
$ = [...$, ...newArr];
}
この場合のプロットはこんな感じ.しっかり円が描かれていますね.

では,実際に メソッドの定義 を見てみましょう.
/**
* Make a new random 3D unit vector.
*
* @method random3D
* @static
* @return {p5.Vector} A new <a href="#/p5.Vector">p5.Vector</a> object
* @example
* <div class="norender">
* <code>
* let v = p5.Vector.random3D();
* // May make v's attributes something like:
* // [0.61554617, -0.51195765, 0.599168] or
* // [-0.4695841, -0.14366731, -0.8711202] or
* // [0.6091097, -0.22805278, -0.7595902]
* print(v);
* </code>
* </div>
*/
p5.Vector.random3D = function random3D() {
const angle = Math.random() * constants.TWO_PI;
const vz = Math.random() * 2 - 1;
const vzBase = Math.sqrt(1 - vz * vz);
const vx = vzBase * Math.cos(angle);
const vy = vzBase * Math.sin(angle);
return new p5.Vector(vx, vy, vz);
};
ん〜なるほど!ランダムで TWO_PI(2π) までの値を取得していること,またこちらの式 Math.sqrt(1 - vz * vz) なんてまさに 原点を中心とした半径1の円の方程式[1] の変形にしか見えません w また vx, vy も,これはどう見ても 極座標[2] ですのでもろに円ですね 😂
今回は2次元のプロットですので vz の値による影響はそれほどないですが,vzBase の値が 0 以上 1 以下となるため vx, vy も同様にその範囲での円のプロットということは,上の画像にも納得です.
ちなみに,ここの定義を愚直に createVector() メソッドを用いて以下のように(引数はテキトー)書いてみましたが,
createVector(random(), random(), random() * 2 - 1);
全く違うプロットになりましたので,p5.Vector.random3D() メソッドを使うことがポイントのようです.

余談: p5.Vector.random2D() メソッドについても見てみましょう
勘の良い方は,今回は結局 2D の絵を描いているのだから p5.Vector.random2D() というメソッドを用いれば良くない?と思われたかと思います.そのご指摘はまっこと仰るとおりで実際に私も試してみましたが,どうもこちらでは違ったプロットになってしまいました.

これはこれで美しいですけどね 😆
一応こちらも メソッドの定義 を見てみました.
/**
* Make a new 2D unit vector from a random angle.
*
* @method random2D
* @static
* @return {p5.Vector} A new <a href="#/p5.Vector">p5.Vector</a> object
* @example
* <div class="norender">
* <code>
* let v = p5.Vector.random2D();
* // May make v's attributes something like:
* // [0.61554617, -0.51195765, 0.0] or
* // [-0.4695841, -0.14366731, 0.0] or
* // [0.6091097, -0.22805278, 0.0]
* print(v);
* </code>
* </div>
*
* <div>
* <code>
* function setup() {
* frameRate(1);
* }
*
* function draw() {
* background(240);
*
* let v0 = createVector(50, 50);
* let v1 = p5.Vector.random2D();
* drawArrow(v0, v1.mult(50), 'black');
* }
*
* // draw an arrow for a vector at a given base position
* function drawArrow(base, vec, myColor) {
* push();
* stroke(myColor);
* strokeWeight(3);
* fill(myColor);
* translate(base.x, base.y);
* line(0, 0, vec.x, vec.y);
* rotate(vec.heading());
* let arrowSize = 7;
* translate(vec.mag() - arrowSize, 0);
* triangle(0, arrowSize / 2, 0, -arrowSize / 2, arrowSize, 0);
* pop();
* }
* </code>
* </div>
*/
p5.Vector.random2D = function random2D() {
return this.fromAngle(Math.random() * constants.TWO_PI);
};
Doc がなげー!のに処理はたった1行やんけ!しかし,やはりこちらもランダムに TWO_PI までの値を取得して利用していますね.
ということで,依存している fromAngle() メソッドの定義 も見てみましょう.こちらも Doc が長いですが(苦笑)
/**
* Make a new 2D vector from an angle.
*
* @method fromAngle
* @static
* @param {Number} angle The desired angle, in radians (unaffected by <a href="#/p5/angleMode">angleMode</a>)
* @param {Number} [length] The length of the new vector (defaults to 1)
* @return {p5.Vector} The new <a href="#/p5.Vector">p5.Vector</a> object
* @example
* <div>
* <code>
* function draw() {
* background(200);
*
* // Create a variable, proportional to the mouseX,
* // varying from 0-360, to represent an angle in degrees.
* let myDegrees = map(mouseX, 0, width, 0, 360);
*
* // Display that variable in an onscreen text.
* // (Note the nfc() function to truncate additional decimal places,
* // and the "\xB0" character for the degree symbol.)
* let readout = 'angle = ' + nfc(myDegrees, 1) + '\xB0';
* noStroke();
* fill(0);
* text(readout, 5, 15);
*
* // Create a p5.Vector using the fromAngle function,
* // and extract its x and y components.
* let v = p5.Vector.fromAngle(radians(myDegrees), 30);
* let vx = v.x;
* let vy = v.y;
*
* push();
* translate(width / 2, height / 2);
* noFill();
* stroke(150);
* line(0, 0, 30, 0);
* stroke(0);
* line(0, 0, vx, vy);
* pop();
* }
* </code>
* </div>
*/
p5.Vector.fromAngle = function fromAngle(angle, length) {
if (typeof length === 'undefined') {
length = 1;
}
return new p5.Vector(length * Math.cos(angle), length * Math.sin(angle), 0);
};
こちらは random3D() メソッドよりも直接的で,sin, cos の値を引数にベクトルのインスタンスを生成しています.見たねは異なりますが処理自体は同じですね.違いは動径(今回のコードで言うところの length と vzBase)の値で,length は何も渡されてないため固定で 1 となり,プロットは予想通り円の枠線になりました(画像は割愛).
どちらも共通しているのは初期生成するベクトルの座標は円の表現をするためのものでした.
② 変化量
コードが多少前後しますが,先に以下のコードを見ます.
// r は上記③で計算した値
return v.add(sin(v.y * r) / 90, cos(v.x * r) / 90);
ここの / 90 の部分は 変化量を小さくしたいのかなと推察されます.これはおそらく単に 流れていくようなプロット にしたいからと考えていますが,予想の粋を出ません.
ここを削除するか 1 に近づけると分かりますが,流れていくようなプロットにはなりません.これは元々の座標位置の値がランダムですので,差分を小さくしないと次の描画位置も見た目上はバラバラになってしまいます.ですので,小さくするために / 90 で小さくしていると思われます.値を徐々に 0 に近づけると挙動が分かりやすいです.[3]
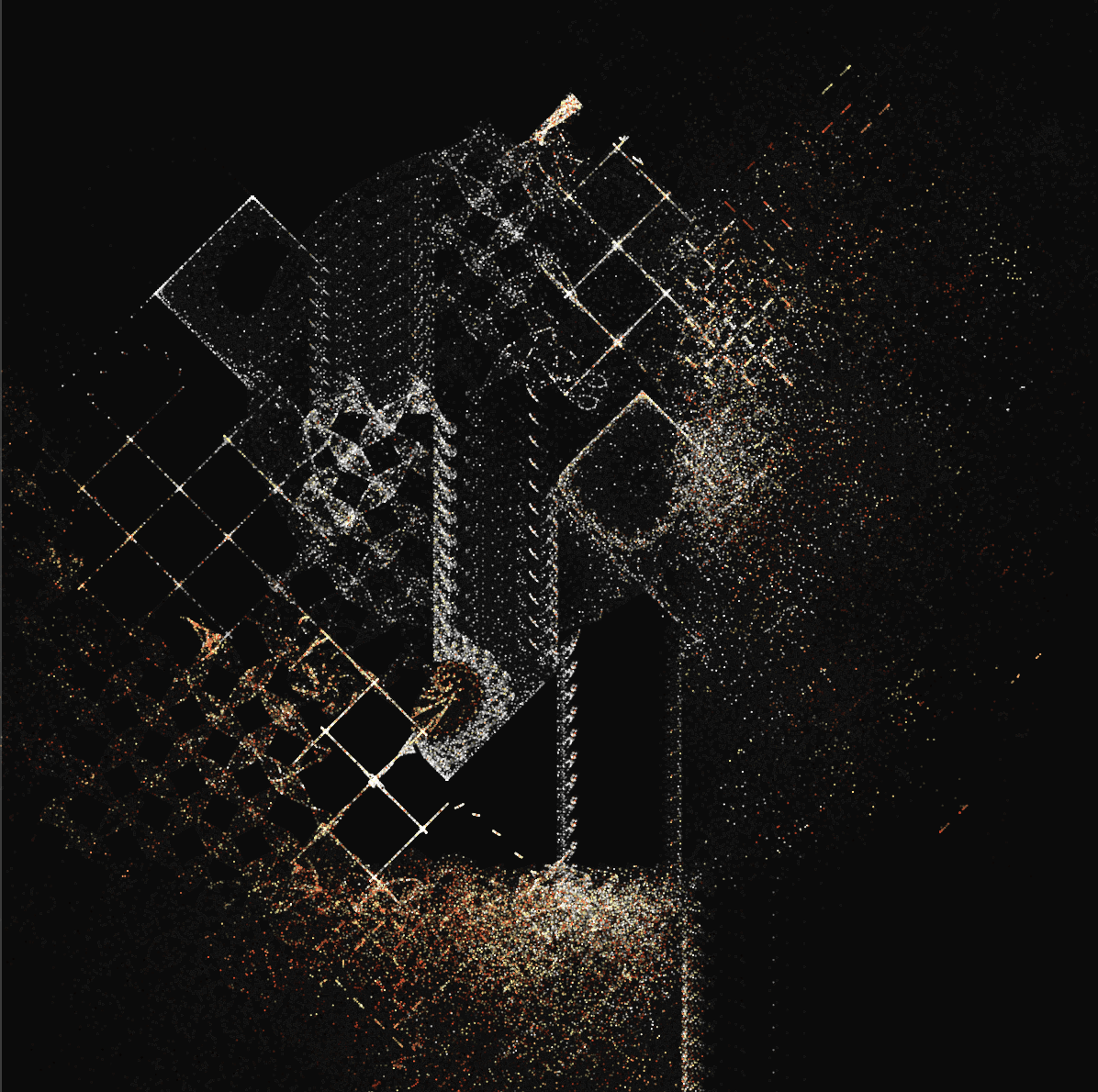
さらに,add() で加算する値を見ると,sin, cos と三角関数ですのでこちらもおそらく距離が 1 の極座標でしょう.では なぜ,四角く表示されるのか? という点ですが,このからくりは 加算する値が三角関数だから となります.
v.add(sin(v.y * r) / 90, cos(v.x * r) / 90);
という式ですが,v.x, v.y 共に時間が経つ連れ値は増えますが,結局加算される値は三角関数です.一応それぞれの要素を数式にしてみますと
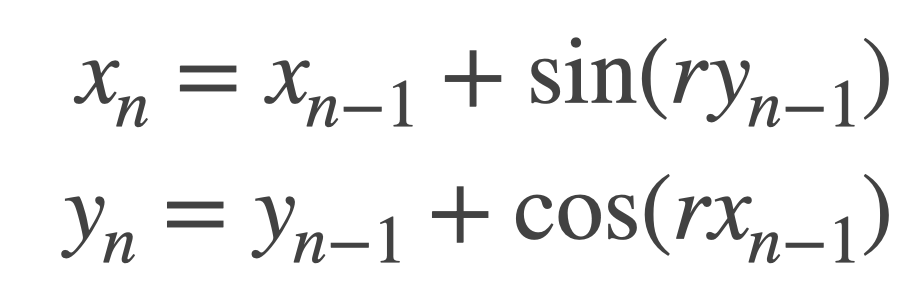
となります.
- x の変化量:
sin - y の変化量:
cos -
sin,cosの微分は対照 - x, y は4象限で向きが変わる
- r の値が大きいほど前の項の影響を受けない
- 直線的なプロットになる
という関係になっており,上記を合わせた結果 半径 r の四角がプロットされる ことになります.
③ ^ (ビット排他的論理和)
すでにだいぶ長く文章が多くて申し訳ないですが,お次は普段見ることが殆どない(個人の感覚です)演算子である,ビット排他的論理和[4] を意味する ^ です[5].電気回路に触れたことがある方は XOR[6] には馴染みがあり,分かりやすいかもしれません.
ビット排他的論理和そのものは説明できますが,私は意図的に使ったことがないのでどういう時に利用するのかちょっと分からず… こちらは どなたかわかる方ご教示いただけますと大変に助かります 🙇
この演算子の左項・右項の値によっては常に値が 0 となり,結果として縦に滝のように流れるプロットとなります.実際に r = 0 と固定にした場合は,以下のようなプロットになります.
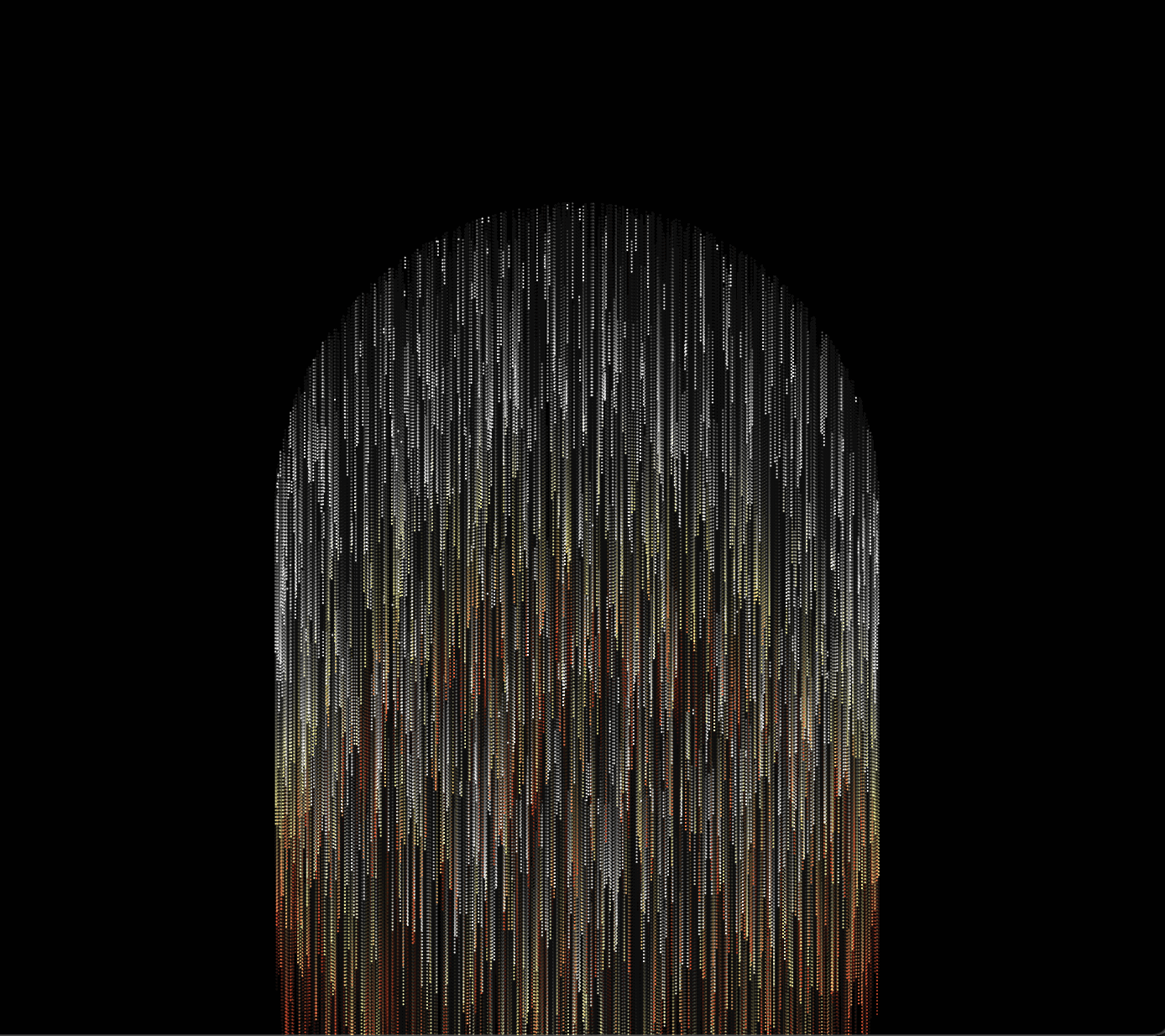
ちなみにここの値を色々変えてみるとそれはそれで面白かったので試してみてください.固定値(今回は 8)の大小によって格子の数が増減します.
以下は r = ((v.x * 2 + 2.5) ^ (v.y + 2)) * 20 にしたときの例.

さらに変数を全て取っ払って固定で r = 20 にしたときの例.

④ 複数の四角(格子状のプロット)
もう一つの謎,なぜ四角が複数個プロットされるのか について.上の r = 20 の例がまさにそれですが,これは ② の話の続きで,
-
x, yは4象限で向きが変わる - 半径
rの値によっては,それぞれの象限で更に別の4象限に移動する可能性がある
結果,複数の四角(いわゆる格子状)にプロットされることになります.[7]
一点面白い結果があるので載せておきます.上記を調べている際に数学のグラフ表示を試していたのですが,x + y だとどうなるのかなーと思って見たところ

このような結果になりました 💁 ここでも格子がプロットされており,歓喜しました(笑)ちなみに x,y の倍数は 2.3 あたりから面白くなります.
余談ですが,今回格子状にプロットにした意図は r の値は x の値によっては大きく変化をすることになります.y は単に + 2 ですが,x は * 2 + 2.5 ですので.したがって,この変化のことを考慮に入れ,複数の格子状の区切りを作っているのが今回のプロットなのかなと予想しています(ここも確信はないですが 🙇)
⑤ 小技その1
stroke() メソッドのレスポンスについて全く調べたことなかったのですが,よく考えれば p5js の組み込みメソッドなんだから prototype で他のメソッドもコールできておかしくないですよね.ということで,メソッドチェーンで stroke().point() とコールすることもできるんですね.
さらに,ベクトルインスタンスも同様で,インスタンスメソッドを v.copy().add(2, 1.6).mult(135) のようにメソッドチェーンで複数個つなげて処理することも可能なんですね.勉強になりました.
ちなみに今回は point() で点描画する際にコピーを生成し,そのコピーの値を
- 加算(
.add(2, 1.6)): 画面上での描画位置を微調整 - 乗算(
.mult(135)): インスタンスの座標位置が画面外にいるので無理やり画面内にずらす
と,されていました.
⑥ 小技その2
if (arr[num]) {
$ = $.slice(20 - num);
} else {
let newArr = [];
for (let i = 0; i < 20; i++) {
newArr.push(p5.Vector.random3D());
}
$ = [...$, ...newArr];
}
この部分ですが,配列の前から古いものを削除(slice)し新しいものを後ろから追加(スプレッド構文 で代入)することで,
- 常に配列の個数を一定に保つ
- 流れていった端の値を初期化
という2つの処理をしていて,これはとても参考になりました.こうすることで点が流れるような表現を生み出せるんですねー.今までシンプルに座標の位置を初期値に戻すとかしかしたことがなかったので,これは新鮮でした 😆
終わりに
実は「こういう数式を組み込んだだけだよ ☆」かもしれませんが,今の自分のググり力では見つからず,愚直に一個一個読み解いてみましたが,思った以上に文章多めで申し訳ない感じです…🙇
更に言うと,理解が浅く雑な点も多いため,間違っていることを書いている可能性は大いにありえます.こちらについては遠慮なくマサカリをいただけますと大変に助かります 🙇
ただ,めちゃくちゃ面白かったですし,久しぶりに数学脳を使ったなーという感覚で,学生時代を思い出しました ❗ やはり数学は美しいなと改めて実感できたのも収穫でした 😆 改めてとても美しい作品を生み出してくださった ア さんに感謝申し上げます.ありがとうございました.
また何か思いついたら分析してみたいと思いますし,今後私が作る作品にも活かしたいと思います ❗
また,明日は 5h5k / Torii さんによる 『何かこしらえて「作ってみた」って言います』 です.お楽しみに ❗
ではでは(=゚ ω ゚)ノ
-
一般的な
x^2 + y^2 = 1 xかyについての式に変形すると導出できます. ↩︎ -
参考リンク: 極座標系(wikipedia) ↩︎
-
個人的には
/ 9 ⇔ 12辺りがいい感じで崩れていて美しいと感じています 😆 ↩︎ -
参考リンク: ビット排他的論理和(MDN) ↩︎
-
累乗計算の
^とは異なる点に注意してください. ↩︎ -
2つの入力が共に真または偽の場合は偽,片方のみが真または偽の場合は真となる論理演算のこと. ↩︎
-
ここも正直に自信がなく,間違っていたら教えていただけますと幸いです 🙇 ↩︎
Discussion