バラ曲線を変化させて美しい絵を描く
こんにちは.株式会社ゆめみ の Keeth こと桑原です.
今回はバラ曲線(rose curve)を触っていて面白いものが描けたので,備忘録として書き残しておきます.
バラ曲線とは?
正葉曲線,通称 バラ曲線(rose curve) とは,ざっくり言うと極座標 (r, θ) において,以下の方程式で表される曲線のことです💁

極座標ですので,直交座標(厳密にはデカルト座標)に変換する必要があり,上記の式で導出された r を用いて以下の式で直交座標に戻してあげます.[1]

上記の式を画面上にプロットすると,以下のような表示になります.

後はこの数式をソースコードに落とし込む作業です 💻
とりあえずデフォルトのバラ曲線を描く
「良いからわしゃあ早くコードが見たいんじゃ!」という方もいらっしゃると思うので,まずはコードの全体を貼っつけます.とりあえず点描しました.
const radius = 150;
let n = 9;
let d = 4;
let x = 0;
let y = 0;
let range = 0;
function setup() {
createCanvas(windowWidth, windowHeight);
stroke(255)
strokeWeight(4);
}
function draw() {
background(0);
translate(width / 2, height / 2);
for (let a = 0; a < d * TAU; a += 0.01) {
// ここがバラ曲線の数式
// radius をかけてあげないとかなり小さな絵になってしまう
range = radius * sin(a * (n / d));
x = range * cos(a);
y = range * sin(a);
point(x, y)
}
}
こんな感じの表示になります.後は n, d の値を自由に変更すればそれぞれの曲線が描かれます.ちなみにオンラインエディタはこちらです.
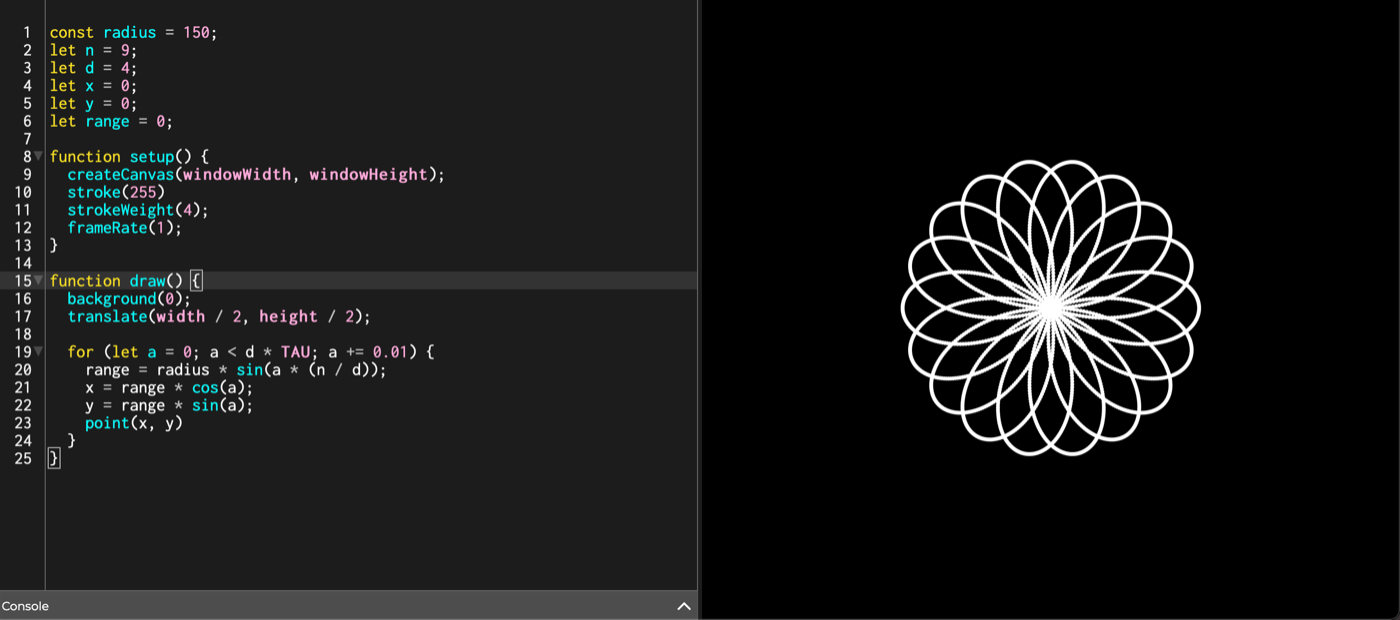
色々弄って遊ぶ
ここから少しずつ変化させて遊んでいきます🙋
アニメーション化
これでも十分美しいですが,ぱっと表示されただけだと見ていて面白くなかったのでアニメーションで少しずつ描くように変更してみました💁オンラインエディタはこちらです.
+ let angle = 0;
function setup() {
createCanvas(windowWidth, windowHeight);
stroke(255)
strokeWeight(4);
- frameRate(1);
+ background(0);
+ angleMode(DEGREES);
}
function draw() {
- background(0);
translate(width / 2, height / 2);
- for (let a = 0; a < d * TAU; a += 0.01) {
- range = radius * sin(a * (n / d));
- x = range * cos(a);
- y = range * sin(a);
- point(x, y)
- }
+ range = radius * sin(angle * (n / d));
+ x = range * cos(angle);
+ y = range * sin(angle);
+ point(x, y)
+ angle += 2;
}
以下のような表示になっていればOKです👍[2]

「点描」から「線描」に変更
点描でも美しいですが,やはり曲線を描きたい(笑)ので線描に変更します🙋
ついでに若干描画速度も上げます.オンラインエディタはこちらです.
let x = 0;
let y = 0;
+ let bx = 0;
+ let by = 0;
function draw() {
(中略)
// 注意: x, y の値の変更の前に書かないとバグります
+ bx = x;
+ by = y;
x = range * cos(angle);
y = range * sin(angle);
- point(x, y);
+ line(bx, by, x, y);
- angle += 2;
+ angle += 3;
}
以下のような表示になっていればOKです👍

余談ですが,この絵に rotate() とか,translate() の座標位置を変更していくと,どんどん曲線が変化し予想しない絵を味わえるのでこれはこれでまた面白いです💁
線に色を付ける
ジェネラティブアートをやられている方なら,とりあえず色をつけたくなると思います(笑)ということで,色を付けていきます.お決まりの HSB モードと frameCount に頼ります😂オンラインエディタはこちらです.
function setup() {
createCanvas(windowWidth, windowHeight);
- stroke(255)
strokeWeight(4);
- background(0);
+ background(100);
angleMode(DEGREES);
+ colorMode(HSB, 100);
}
function draw() {
translate(width / 2, height / 2);
+ stroke(frameCount % 100, 100, 100);
}
こうなっていればOK👍時間経過によって線が上書きされていく様を見ることができますね.

angle の値を大きくする
この後の見た目のために,先程の色の設定を戻しておきます.
御存知の方もいらっしゃると思いますが line() 関数は 曲線ではなく直線の接続 のため,先程の angle の値を大きくしすぎる(つまり変化量を大きくする)とカクついてしまいます.例えば angle = 8 辺りにすると目で見てもカクついているのが分かると思います.
ですが,この値を更に大きくしていくととたんに世界が変わります(大袈裟😂).
試しに n = 9, d = 4, angle = 10 にした図がこちらです.
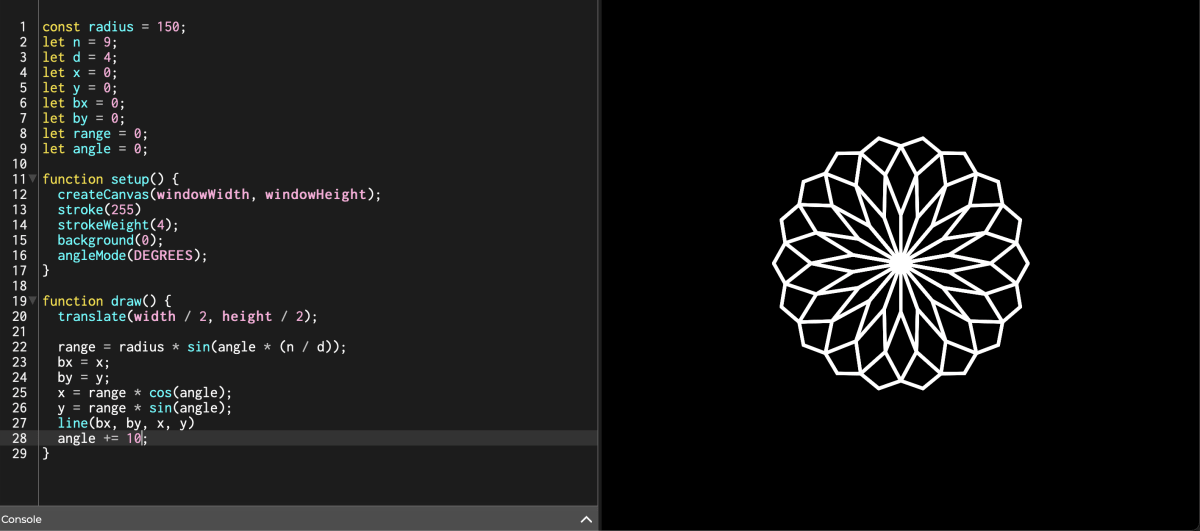
上手いこと各線分の頂点同士が重なり合って 結晶のように見えませんか? 偶然この絵を見つけましたが,線分の長さといわゆる「葉」の部分が描かれる angle の周期を考えると納得が行くかもしれません(?)
ではさらにこの値を大きくしてみましょう.angle = 22, 28, 32, 35 辺りの絵が個人的には好きですね💁[3]

こちらは重なる周期がかなり遅くなってしまいますが,何度も塗りつぶされることで 魔法陣・エンブレム のような見た目に大変身したではないですか.個人的にはこの絵が描かれる過程も見ていて面白かったです😄
ちなみにこの状態で先程のように色をつけますと,流石にエンブレム調の方は色が多すぎて五月蝿いかなと感じました.逆に stroke の色の設定(第一引数)を以下のように
- stroke(frameCount() % 100, 100, 100);
+ stroke(millis() % 100, 100, 100);
変化を速くしてみますと,これはまた面白い見た目になるので試してみてください💁
終わりに
いかがだったでしょうか?人によっては子供のときに遊んだ スピログラフ を思い出された方もいらっしゃるかもしれません.改めて数学の美しさと偶然性と共存する楽しさを味わえた時間だったので,ご興味ある方は試してみてくださいー.
ではでは(=゚ω゚)ノ
Discussion