[ABC266] AtCoder Beginner Contest 266(A-F 問題 Python)
AtCoder Beginner Contest 266 の復習記録です。難易度が青色レベル以下の、A問題からF問題までをやります。使用言語はPythonです。
A問題
考え方
文字列の長さと、中央の文字のインデックスを比較してみます。
| 文字列の長さ | 中央の文字 |
|---|---|
| 3 | 1 |
| 7 | 3 |
| 15 | 7 |
提出コード
S = input()
n = len(S)//2
print(S[n])
B問題
考え方
ただし
| 1 | 1 | 0 |
| 100 | 100 | 0 |
| 998244354 | 1 | 998244353 |
| 100 + 998244353 | 100 | 998244353 |
| 998244352 + 998244353 | 998244352 | 998244353 |
具体的な数字を考えると、
提出コード
N = int(input())
M = 998244353
ans = N%M
print(ans)
C問題
考え方
公式解答によると、ベクトルの外積を用いると簡単なようです。
思いつかなったので、直線と領域で考えて実装しました。
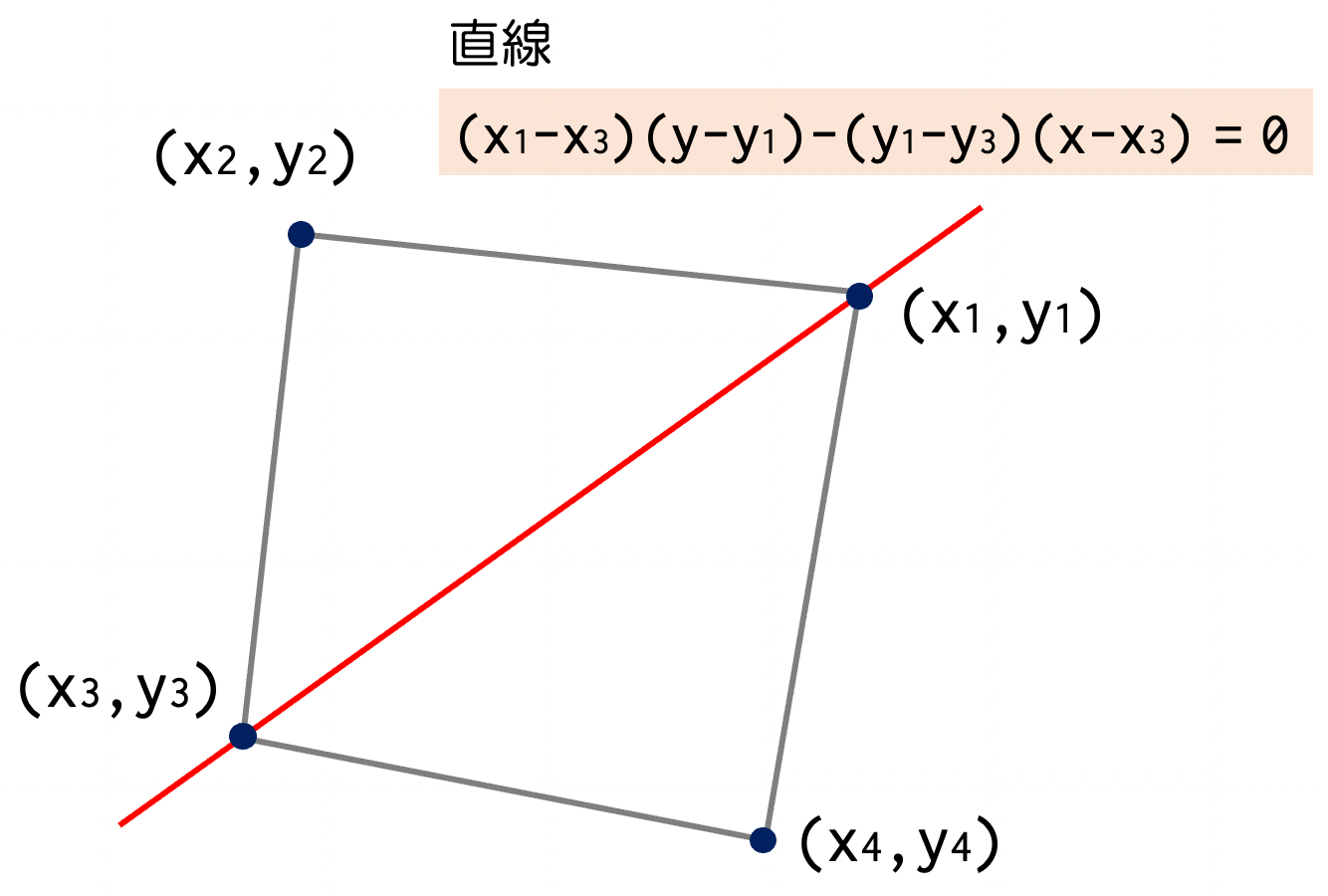
凸の四角形のときには、対角線で分けられる2つの領域に、直線以外の2点が分配されます(正負が分かれます。そのため、かけ算すると負になります)。

このことを、直線ACに対するB,Dの位置を考えた場合と、直線BDに対するA,Cの位置を考えた場合のそれぞれについて判定します。
提出コード
Ax,Ay=map(int,input().split())
Bx,By=map(int,input().split())
Cx,Cy=map(int,input().split())
Dx,Dy=map(int,input().split())
def solve(x1,x2,x3,x4,y1,y2,y3,y4):
if ((x1-x3)*(y2-y3)-(y1-y3)*(x2-x3))*((x1-x3)*(y4-y3)-(y1-y3)*(x4-x3))<0:
return True
else:
return False
flag1 = solve(Ax,Bx,Cx,Dx,Ay,By,Cy,Dy)
flag2 = solve(Dx,Cx,Bx,Ax,Dy,Cy,By,Ay)
if flag1 and flag2:
print("Yes")
else:
print("No")
D問題
考え方
DP[
すぬけ君が出現する場所にいられたときには、スコアを更新します。
提出コード
N = int(input())
# すぬけ君が出現する時間、座標を記録します
event = []
for _ in range(N):
T,X,A = map(int,input().split())
event.append([T,X,A])
# 時間の最大値をTmとして、DPテーブルを準備します
Tm = T
DP = [[-1]*(Tm+1) for _ in range(5)]
DP[0][0] = 0
i = 0
for t in range(Tm):
T,X,A = event[i]
for x in range(5):
if DP[x][t] < 0:
continue
if x < 4:
P = A if X == x+1 and T == t+1 else 0
DP[x+1][t+1] = max(DP[x+1][t+1],DP[x][t]+P)
if x > 0:
P = A if X == x-1 and T == t+1 else 0
DP[x-1][t+1] = max(DP[x-1][t+1],DP[x][t]+P)
P = A if X == x and T == t+1 else 0
DP[x][t+1] = max(DP[x][t+1],DP[x][t]+P)
# すぬけ君の出現イベントが起きたら、iを増やします
if T == t+1:
i += 1
ans = max([DP[x][Tm] for x in range(5)])
print(ans)
E問題
考え方
具体的に
1回目のダイスで、例えば、6の目が出たならば、それで終わりにする方が得です。
1の目が出たならば、次のラストチャンスに賭ける方が得になります。
4の目が出たならば、次の回の期待値(3.5)を考えると、それで終わりにする方が得と考えられます。
3の目が出たならば、もう1回振る方が得です。
つまり、
{1,2,3,4,5,6} の各出目と、
提出コード
N = int(input())
DP = [0]*(N+1)
for i in range(1,N+1):
t = 0
for x in range(1,7):
t += max(x, DP[i-1])
DP[i] = t/6
ans = DP[N]
print(ans)
F問題
考え方
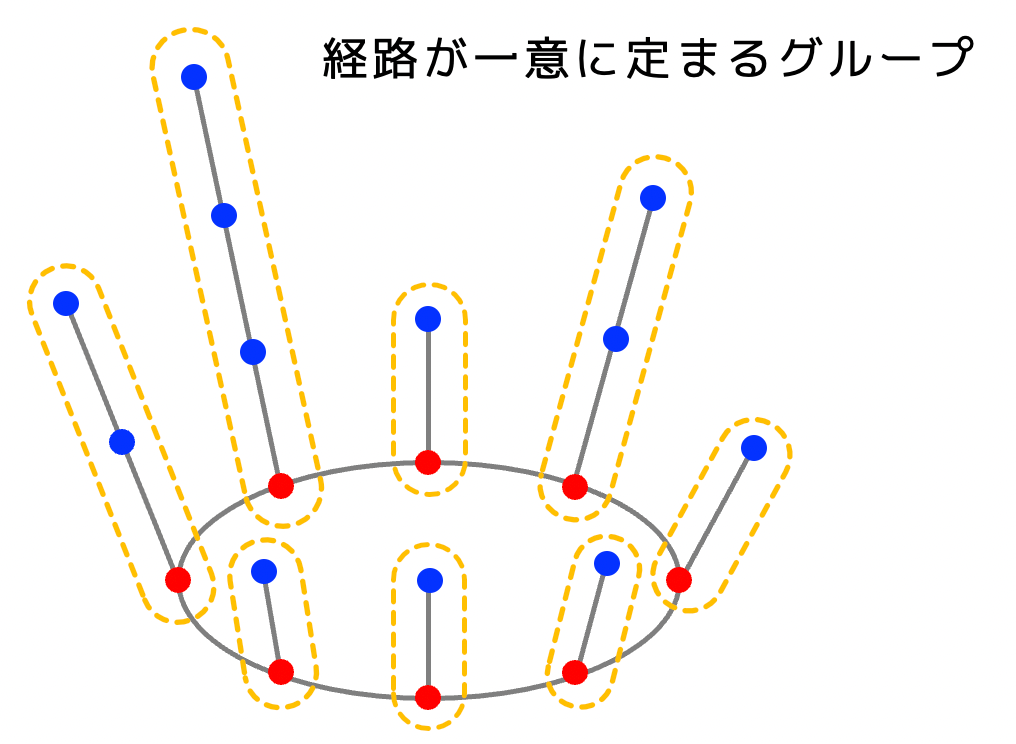
頂点の出次数を記録しておき、出次数1の頂点を順番にチェックします。出次数1の頂点と、その辺を消去するとともに、union-findを用いて、グループ分けをしていきます。

提出コード
import sys; sys.setrecursionlimit(10**6)
from collections import deque
N = int(input())
d = [0] * N
E = [[] for _ in range(N)]
root = [i for i in range(N)]
def find(x):
if root[x]==x:
return x
root[x] = find(root[x])
return root[x]
def unite(x,y):
rx = find(x)
ry = find(y)
if rx == ry:
return
root[rx] = ry
# 出次数の記録
for _ in range(N):
u,v = map(int,input().split())
u-=1; v-=1
E[u].append(v)
E[v].append(u)
d[u] += 1
d[v] += 1
# 出次数1の頂点をdequeに入れる
dq = deque()
for i in range(N):
if d[i] == 1:
dq.append(i)
# 出次数1の頂点を順番にチェックする
# 頂点を消して、辺を消して、i-jを同じグループにする
while dq:
i = dq.popleft()
j = E[i][0]
d[i] -= 1
d[j] -= 1
E[j].remove(i)
unite(i,j)
if d[j] == 1:
dq.append(j)
# クエリ処理では、x-yが同じグループなら、一意に定まる
Q = int(input())
for _ in range(Q):
x,y =map(int,input().split())
x-=1; y-=1
if find(x) == find(y):
print("Yes")
else:
print("No")
Discussion