[EDPC-N問題 Slimes] Educational DP Contest を Pythonで解く

はじめに

競技プログラミング（使用言語はPython）を日々精進中です。
DP（動的計画法）をマスターするために、AtCoderのEducational DP Contestを解いています。

N問題 Slimes

https://atcoder.jp/contests/dp/tasks/dp_n

問題概要

$N$ 匹のスライムがいて、大きさは $a_i$ で与えられる。となり合ったスライムは合体でき、大きさ $x$ のものと大きさ $y$ のものの合体コストは、 $x+y$ となる。全部のスライムを合体させるときに、合体コストの最小値を求める。

考え方

$DP$ [ $L$ ][ $R$ ]を $L$ から $R$ までを合体させたときの合計コストの最小値と定義する。
求める値は $DP$ [ $0$ ][ $N$ ]となる。

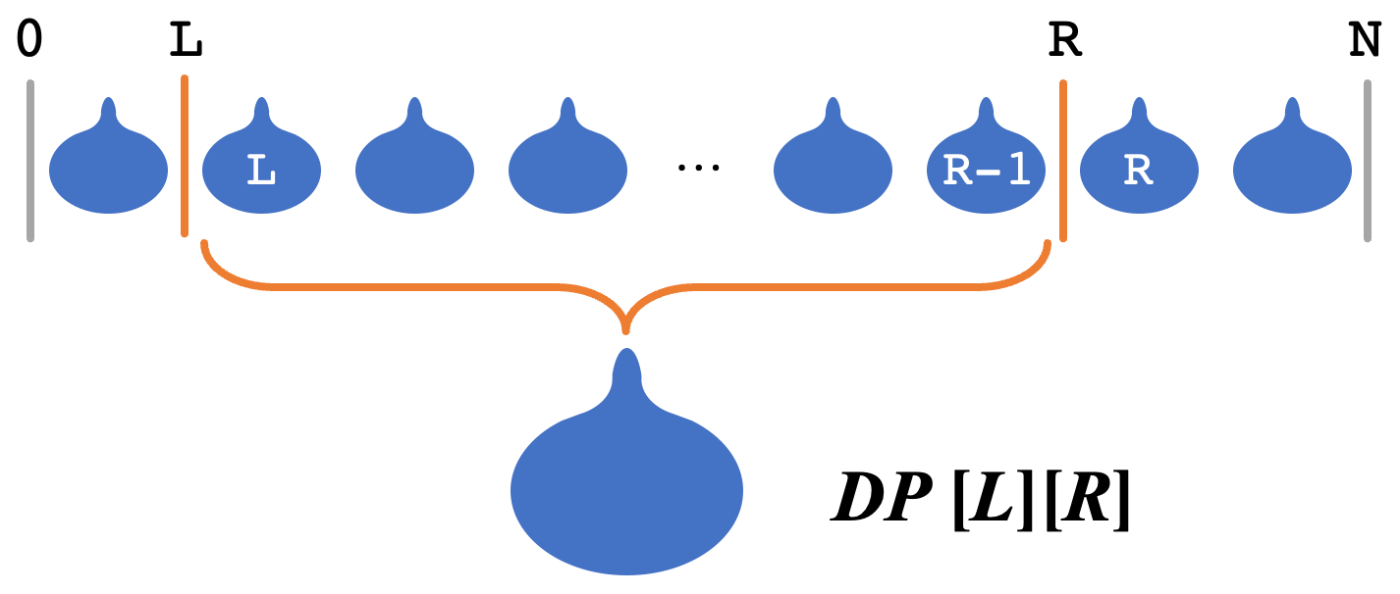
注意するポイントとしては、$L$, $R$ は仕切りで考えること。そのため、 $0≦L<R≦N$ となる。

DP遷移の考え方は、 $L$ から $R$ の区間のスライムを1つにする一手前の状態を考え、分ける境界を全探索してコストの最小値を求める。

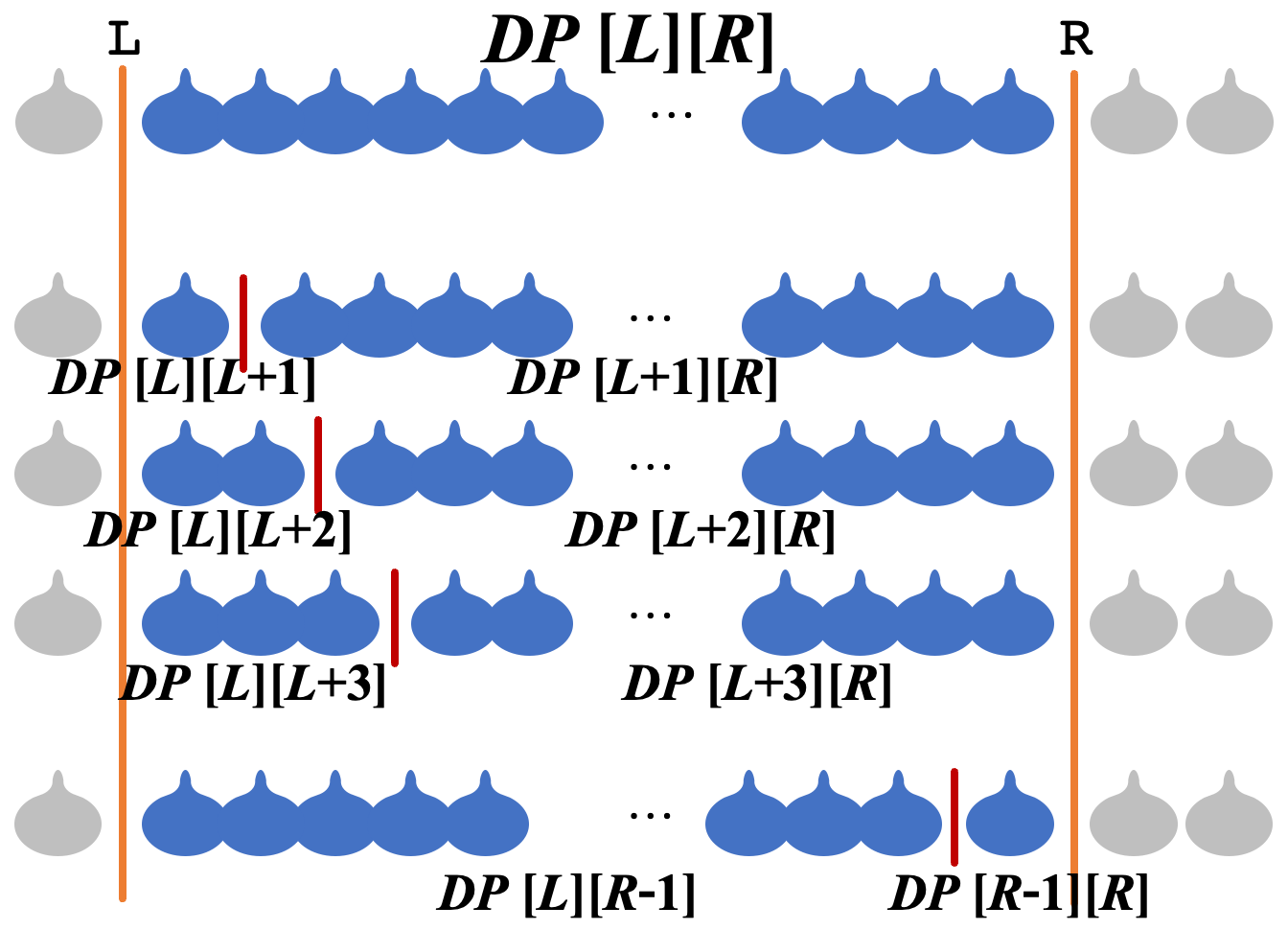
こう考えると $DP$ [ $L$ ][ $R$ ]は、前段階の中でコストが最小のものに、今回の合体でのコストを加算したものとなる。

$$DP[L][R] = \operatorname*{\min}\limits_{1≦i<R-L} (DP[L][L+i]+DP[L+i][R]) + \operatorname*{sum}\limits_{L≦i<R}a_i$$

一番後ろの区間和の項については、累積和を前計算しておき、高速で計算できるようにしておく。

実装メモ

メモ化再帰関数で実装した。

N = int(input())
A = list(map(int,input().split()))
INF = 10**18
S = [0]
for a in A:
    S.append(S[-1]+a)

DP = [[-1]*(N+1) for _ in range(N+1)]
for i in range(N):
    DP[i][i+1] = 0

def dp(l,r):
    if DP[l][r] >= 0:
        return DP[l][r]
    
    ret = INF
    for i in range(1,r-l):
        ret = min(ret, dp(l,l+i)+dp(l+i,r))
    ret += S[r]-S[l]

    DP[l][r] = ret
    return ret

ans = dp(0,N)
print(ans)