😸
[ABC261F] Sorting Color Balls を Pythonで解く
考え方
転倒数の問題です。ボールの数字が昇順となるように、並び替えるときの交換回数を求める問題です。ボールを並び替えたときの線の交点を数えれば良いですが、ボールの色が同じときは、数えないため、下図の赤交点のみカウントして、青交点はカウントしません。
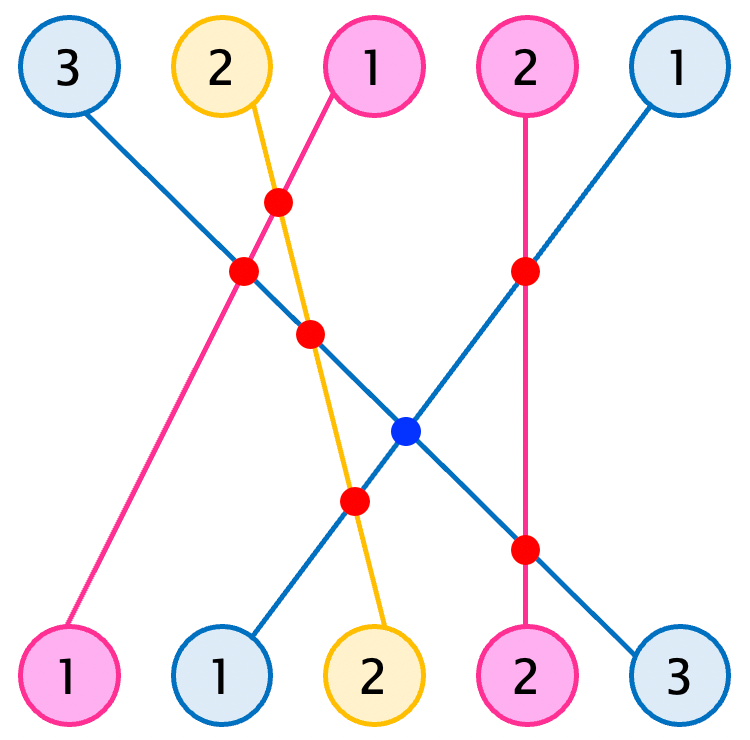
まずは、色がない場合で考えてみます。
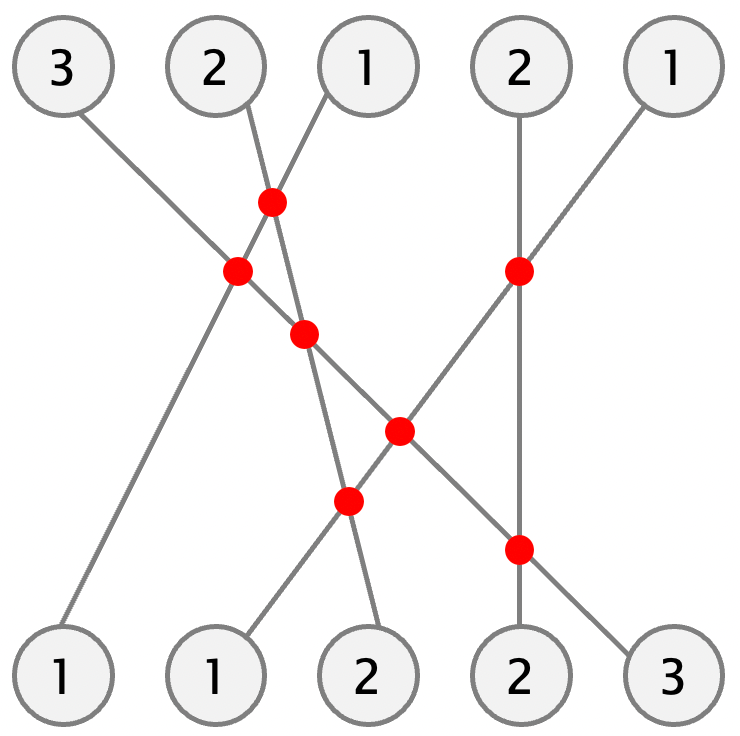
これは、ボールの数字を左から順番に見ていった場合に、既に見た数の中で、今の数よりも大きいものを数えて合計すれば良いです。
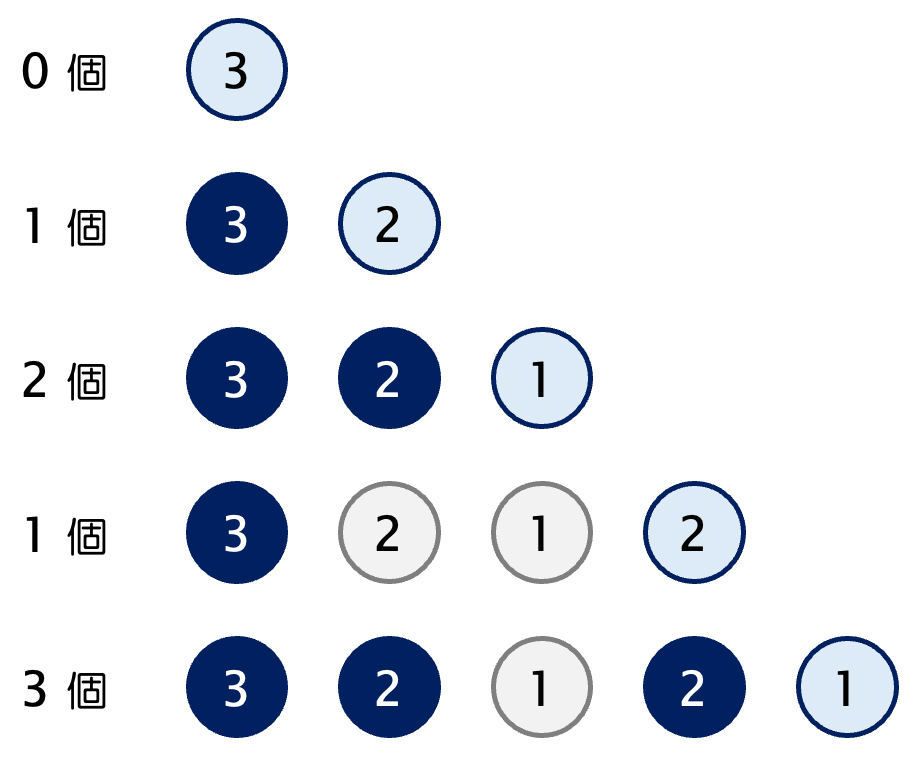
あとは、「ボールの色が同じ場合はカウントしない」という条件を加えれば良いです。計算量を考えなければ、下記で正しい出力は得られます。
# これだとTLEになる
N = int(input())
C = list(map(int,input().split()))
X = list(map(int,input().split()))
ans = 0
for i in range(N):
for j in range(i):
if C[j] == C[i]:
continue
if X[j] > X[i]:
ans += 1
print(ans)
この実装が、TLE(Time Limit Exceeded) となってしまうのは、既に見た数の中から、今の数よりも大きいものを探すという操作で、愚直に線形探索をしているからです。セグメント木やフェニック木などを用いて、区間データに数字をカウントしていけば、計算量を減らすことができます。
実装メモ
セグメント木を用います。
色を考えない場合を求めてから、各色ごとに交点(転倒数)を求めて減算すれば良いです。

from collections import defaultdict
N = int(input())
C = list(map(int,input().split()))
X = list(map(int,input().split()))
def f(x,y):
return x+y
def update(X,Y):
X += Leaf
D[X] = f(D[X],Y)
X >>= 1
while X > 0:
D[X] = f(D[X*2], D[X*2+1])
X >>= 1
def query(L,R):
L += Leaf; R += Leaf
ret = 0
while L < R:
if L % 2 == 1:
ret = f(ret, D[L])
L += 1
if R % 2 == 1:
R -= 1
ret = f(ret, D[R])
L >>= 1; R >>= 1
return ret
色を考えない場合の転倒数を求めながら、色ごとのグループを調べておきます。
ColorGroup = defaultdict(list)
ans = 0
Leaf = 1 << N.bit_length()
D = [0] * Leaf * 2
for i in range(N):
ColorGroup[C[i]].append(X[i])
ans += i - query(0, X[i]+1)
update(X[i],1)
セグメント木を初期化して、各色ごとの交点(転倒数)を求めます。1つの色(グループ)を見終わったら、セグメント木のデータを巻き戻して初期化します。
D = [0]*Leaf*2
for lis in ColorGroup.values():
for i in range(len(lis)):
ans -= i - query(0,lis[i]+1)
update(lis[i],1)
for i in range(len(lis)):
update(lis[i],-1)
print(ans)
考察
色ごとの初期化操作のときに、
D = [0]*Leaf*2
としてもセグメント木のデータは初期化されますが、リストの定義に計算時間がかかるようです。
最後の部分を下記のようにすると、TLEとなりました。
# これだとTLEとなった
for lis in ColorGroup.values():
D = [0]*Leaf*2
for i in range(len(lis)):
ans -= i - query(0,lis[i]+1)
update(lis[i],1)
Discussion