Zenn
🍊

[EDPC-Y問題 Grid 2] Educational DP Contest を Pythonで解く

2022/06/26に公開
Python
競技プログラミング
AtCoder
tech

はじめに

競技プログラミング（使用言語はPython）を日々精進中です。
DP（動的計画法）をマスターするために、AtCoderのEducational DP Contestを解いています。

Y問題 Grid 2

https://atcoder.jp/contests/dp/tasks/dp_y

問題概要

縦H行×横W列のグリッド上に、N個の壁マス（障害物）がある。
マス(1,1)から出発して、右または下への移動を繰り返して、マス(H,W)まで到達するときの移動経路を考える。（10^9+7で割った余りで答える）

制約

グリッドは大きいが、障害物はあまり多くない。
2 ≦ H, W ≦ \def\bar#1{#1^5} \bar{10}
1 ≦ N ≦ 3000

考え方

障害物がなければ、マスの移動経路の場合の数は、右移動、下移動の並び替えで計算できます。

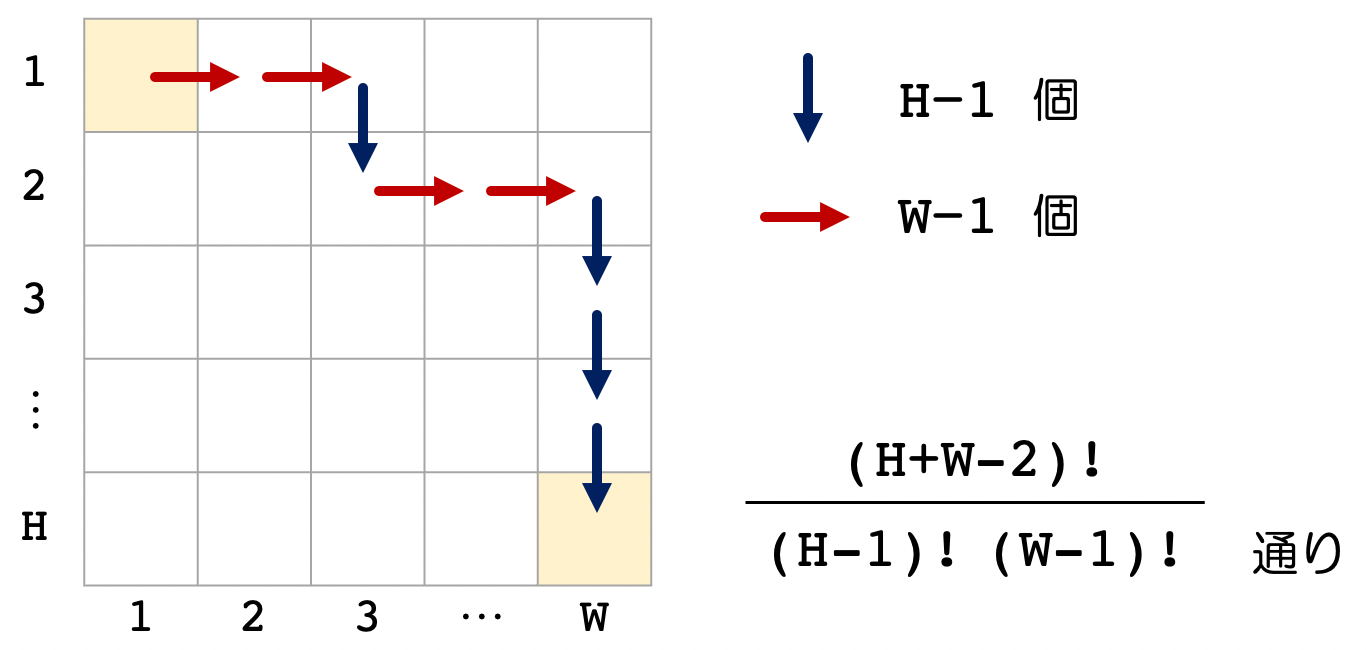
階乗の割り算が出てくるため、逆元の処理を行う必要があります。逆元の説明は、今回はパスしますので、他の記事を参照して下さい。

障害物の処理については、包除原理を用います。包除原理とは和集合の要素数に関する以下のような法則です。

この数式を見ると、ベン図の加算・減算を思い出しますね。おそらく、これと同じような意味合いだと思います。

数学的に正確な記述ではないかもしれませんが、考える集合の個数が増える度に、加算・減算が交互になるということですね。

この包除原理を経路問題にどう用いるかというと、障害物が1つであれば、スタートからゴールへ移動する全ての移動経路（水色）から、障害物を通る経路（ピンク色）を減算すれば、障害物を通らない経路を求められます。

障害物が2つであれば、障害物を1つだけ通る経路は減算しますが、障害物を2つ通る経路は、2回重複して減算しているため、反対に加算する必要があります。

包除原理から、障害物を3つ通る場合には減算、障害物を4つ通る場合には加算、…というように、続いていくことになります。つまり、奇数個の障害物を通る場合には減算、偶数個の障害物を通る場合には加算です。

移動は右移動・下移動のみで、戻ることはないため、障害物を複数通るときには、行数r,列数cはともに、先に通った障害物よりも、後に通る障害物で大きくなります。

実装メモ

便宜上、obs[0]にスタート地点(1,1)を入力し、obsに障害物の座標をappendで記録し、その後でobsを昇順にしておく。DP[i][0]は、障害物iまでに偶数個の障害物を通って到達する経路数、DP[i][1]は、障害物iまでに奇数個の障害物を通って到達する経路数と定義する。

H,W,N=map(int,input().split())
mod = 10**9+7
M = H+W
obs = [[1,1]]
DP = [[0]*2 for _ in range(N+1)]
DP[0][0] = 1

for _ in range(N):
    r,c=map(int,input().split())
    obs.append([r,c])

obs.sort(key=lambda x: x[1])
obs.sort(key=lambda x: x[0])

並び替えの計算があるため、逆元のリストを作成する。階乗の計算は、M (H+W) を超えることはないため、Mまで準備しておく

def modinv_cal(p,a):
    r,q = 1, p-2
    while q:
        if q % 2 == 1:
            r *= a
            r %= p
        q >>= 1
        a = (a**2) % p
    return r

fact = [1] * (M+1)
invfact = [0] * (M+1)

for i in range(1,M+1):
    fact[i] = (fact[i-1]*i) % mod

invfact[-1] = modinv_cal(mod,fact[-1])

for i in range(M,0,-1):
    invfact[i-1] = (invfact[i]*i) % mod

右移動w回、下移動h回での移動経路の場合の数を計算する関数 move(h,w) を準備する。

def move(h,w):
    r = fact[h+w]
    r *= invfact[h]; r %= mod
    r *= invfact[w]; r %= mod
    return r

DPの計算部分では、障害物iとそれより前に通る可能性のある経由障害物jを考える。DP[j][0]は、障害物jまでで偶数個の障害物を通っている。それに障害物iの1個分が加わり、障害物の個数の偶奇が変化するため、DP[i][1]に加えることになる。move(ri-rj,ci-cj)は、jからiまでの移動経路である。同様にして、DP[j][1]からDP[i][0]が計算できる。

for i in range(1,N+1):
    ri,ci = obs[i]
    for j in range(i):
        rj,cj = obs[j]
        if rj<=ri and cj<=ci:
            DP[i][0] += DP[j][1] * move(ri-rj,ci-cj)
            DP[i][0] %= mod
            DP[i][1] += DP[j][0] * move(ri-rj,ci-cj)
            DP[i][1] %= mod

答えの計算では、包除原理の考え方から、障害物iまでに偶数個の障害物を通ってきていたものは加算、奇数個の障害物を通ってきていたものは減算する。move(H-ri,W-ci)は、障害物iからゴール地点までの移動経路である。

ans = 0
for i in range(N+1):
    ri,ci = obs[i]
    ans += DP[i][0] * move(H-ri,W-ci)
    ans %= mod
    ans -= DP[i][1] * move(H-ri,W-ci)
    ans %= mod

print(ans)

Discussion