🐮

[ABC259F] Select Edges を Pythonで解く

2022/07/18に公開

Python

競技プログラミング

AtCoder

tech

考え方

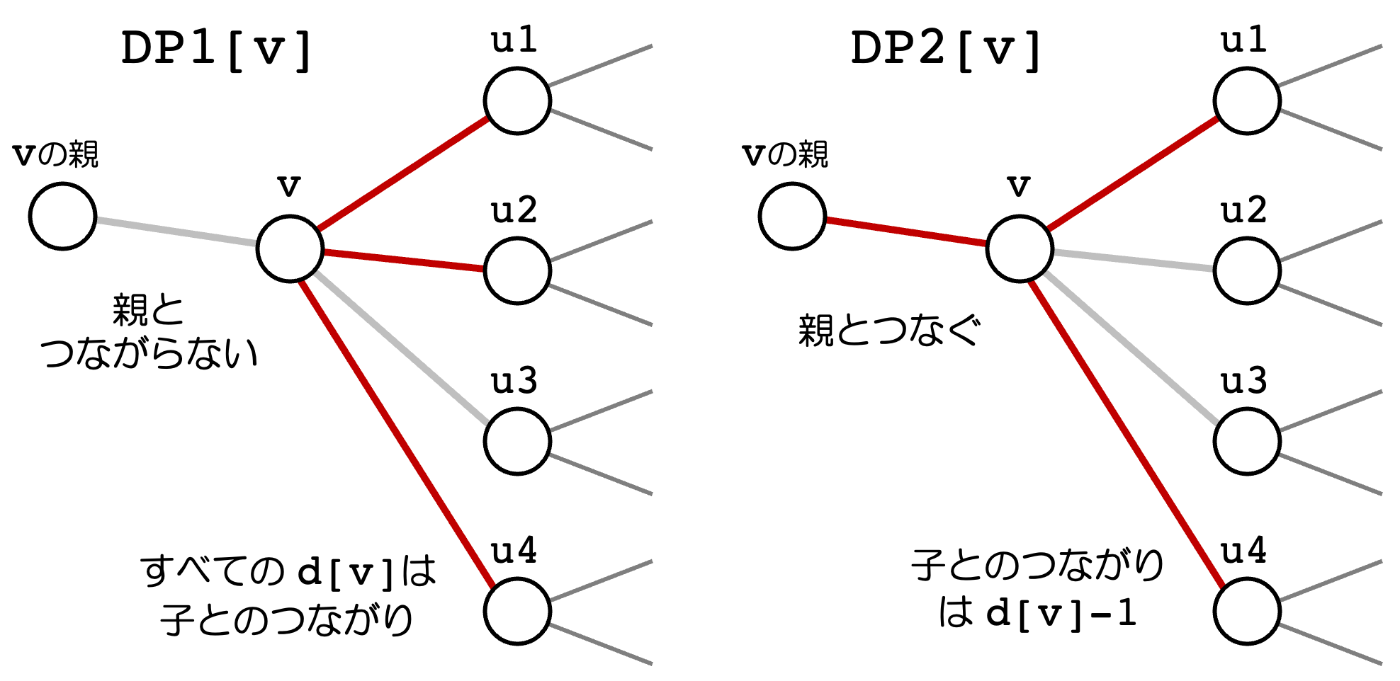
木DPで解きます。ある頂点 $v$ に対して $v$ より下位の重みの総和の最大値をDPで考えていきます。他の頂点とのつながり回数（辺の選択）に制限 d[ $v$ ] があり、親とつながりがあるか否かで、子とのつながり回数が変わるため、下記のようにDPを2種類準備します。

親とのつながりを"持たない"場合の $v$ より下位の重みの総和の最大値が DP1[ $v$ ] であり、つながり制限回数の全てを子とのつながりに使います。親とのつながりを"持つ"場合の $v$ より下位の重みの総和の最大値が DP2[ $v$ ] であり、子とのつながり回数は1回減ります。

辺の重みが正であれば、つなぐ方が重みの総和は大きくなりますので、通常は、DP2[ $u_x$ ]を選んだ方がより重みの総和は大きくなりそうです。しかし、回数制限があるので、DP2[ $u_x$ ]ばかりは選べず、いくつかの子についてはDP1[ $u_x$ ]を選ばないといけないかもしれません。そのため、始めはDP1[ $u_x$ ]を選んでおいて、DP2[ $u_x$ ] $-$ DP1[ $u_x$ ] が大きいものから、DP2[ $u_x$ ] に変更していきます。辺の重みが負の場合は、DP2[ $u_x$ ]がDP1[ $u_x$ ]よりも小さくなるので、自然とDP2[ $u_x$ ]は選択されなくなります。

DP1[ $v$ ]、DP2[ $v$ ]を決めるには、その子 $u_x$ のDP1[ $u_x$ ]、DP2[ $u_x$ ]が計算済みである必要があります。そのため、始めにBFS(幅優先探索)を行い、親子関係を決定(深さのレベルを記録)しておき、子の方から計算するようにします。

実装メモ

from collections import deque
N = int(input())
d = list(map(int,input().split()))
E = [[]*N for _  in range(N)]
DP1 = [0] * N
DP2 = [0] * N

for _ in range(N-1):
    u,v,w=map(int,input().split())
    u-=1; v-=1
    E[u].append([v,w])
    E[v].append([u,w])

BFS(幅優先探索)を行い、親子関係を決定する。
深さレベルをlevelに記録する(レベルが大きい方が下位・子となる)。
$0$ を根とした木で考え、BFSで評価した順番をarrに記録しておく。これを反対からたどれば子から親の順番となる。

level = [-1] * N
def BFS(s):
    level[s] = 0
    dq = deque([s])
    arr = [s]
    
    while dq:
        v = dq.popleft()
        for u,w in E[v]:
            if level[u] >= 0:
                continue
            level[u] = level[v] + 1
            dq.append(u)
            arr.append(u)
    return arr

arr = BFS(0)
arr.reverse()

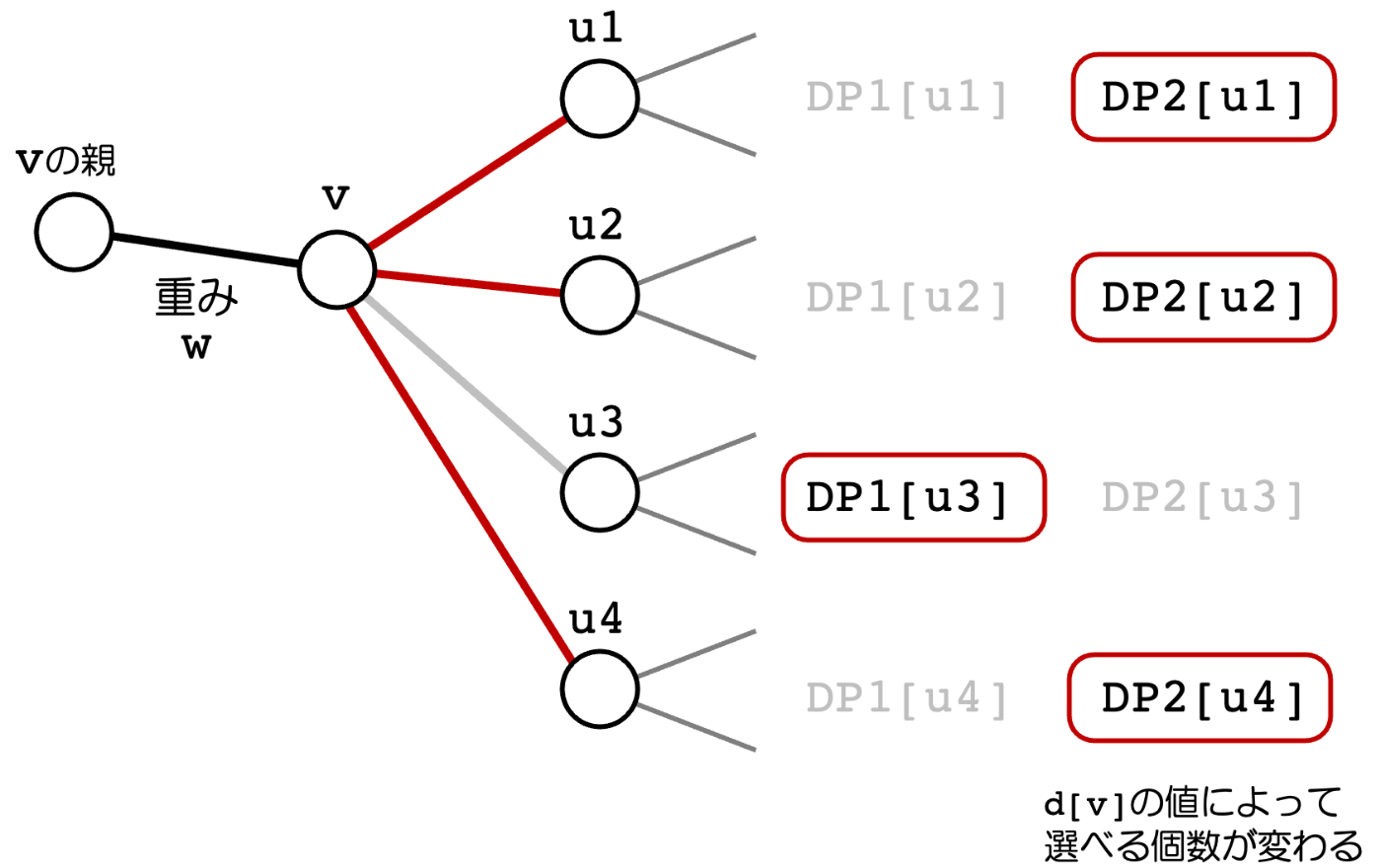
$v$ と連絡辺がある点を順番に見ていく。levelを比較して親子関係を評価して、親ならば、DP2[ $v$ ]にはwを加えるが、DP1[ $v$ ]には加えない。子ならば、DP1[ $v$ ]、DP2[ $v$ ]の両方にDP1[ $u_x$ ]をとりあえず加えておく。
子の場合にはさらに、DP2[ $u_x$ ] $-$ DP1[ $u_x$ ]を dif に記録しておき、全ての頂点を見終わった後に dif を大きい順に並び替え、大きい方から、DP1[ $v$ ]であればd[ $v$ ]個、DP2[ $v$ ]であればd[ $v$ ] $-1$ 個は、DP2[ $u_x$ ]の方を選ぶようにする。
dif にはDP2[ $u_x$ ] $-$ DP1[ $u_x$ ]が記録されているので、 dif の前からd[ $v$ ]個またはd[ $v$ ] $-1$ 個を足せば、差分を足すので、DP2[ $u_x$ ]の方を選んだ値に変換される。

def CntDP(v):
    dif = []
    for u,w in E[v]:
        if level[u] < level[v] and d[v] > 0:
            DP2[v] += w
        else:
            if DP2[u]-DP1[u] > 0:
                dif.append(DP2[u]-DP1[u])
            DP1[v] += DP1[u]
            DP2[v] += DP1[u]
    
    dif.sort(reverse=True)
    
    if len(dif) > 0:
        DP1[v] += sum(dif[:d[v]])
        if d[v] > 0:
            DP2[v] += sum(dif[:max(d[v]-1,0)])

for v in arr:
    CntDP(v)

ans = DP1[0]
print(ans)

少しまどろっこしい実装になってしまいましたが、pythonでのAC(Accepted)コードの中では、実行時間も短めでメモリ量も少ない方だったので、良しとしました。

考え方

実装メモ

Discussion