燃やす埋める問題(最大フロー最小カット問題)について整理する [理解編]
はじめに
今回は、燃やす埋める問題と呼ばれるタイプの問題(Project Selection Problemと呼ばれることもある)を考えていきます。グラフ理論(離散数学)の中の最大フロー最小カットという分野が関連していますので、そのあたりも一緒に整理していきます。問題はAtCoderの過去問題からピックアップして解いていく予定です。
最小カットとは
s, t を端点とする有向グラフがあり、それぞれの辺に容量が設定されている場合を考えます。
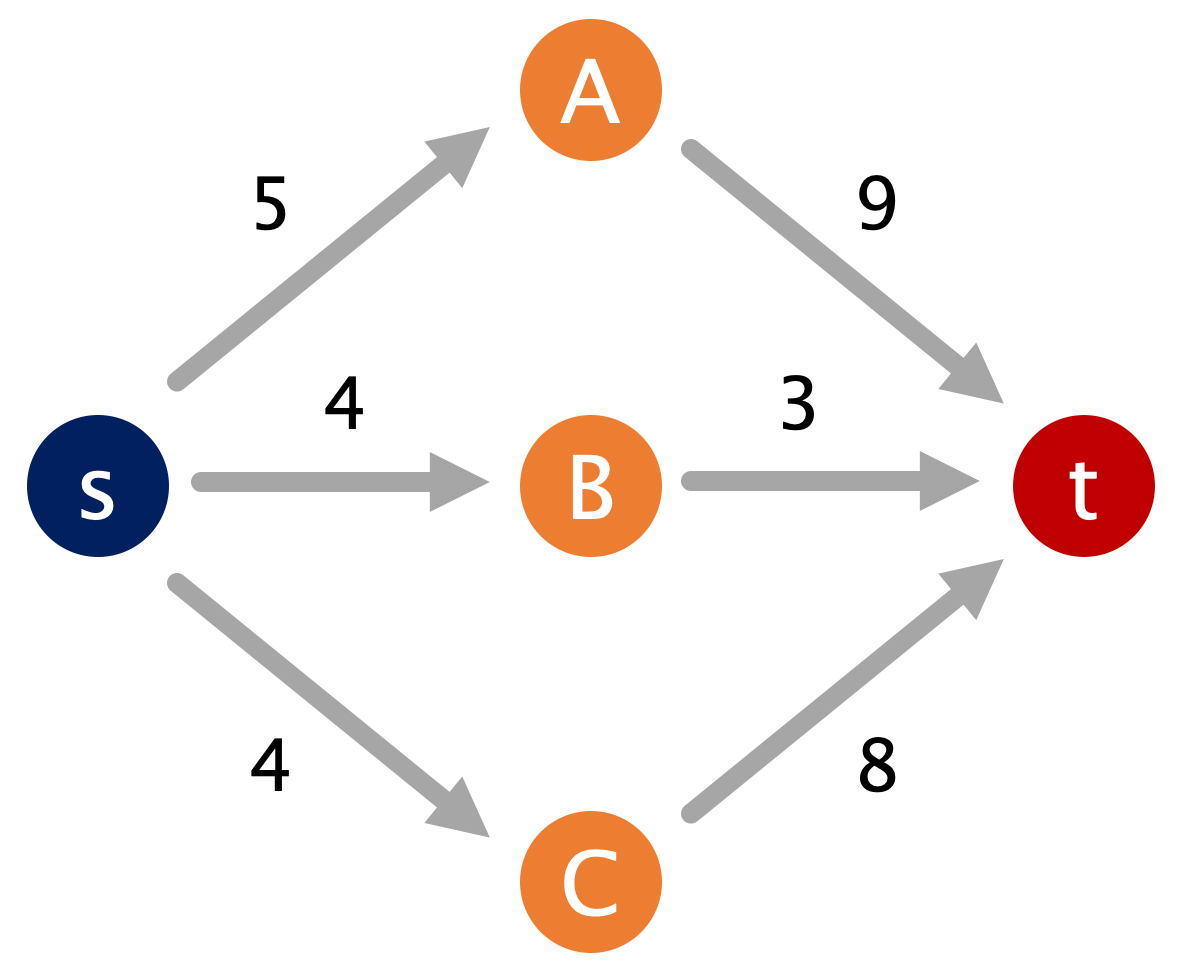
ここで、s, t 以外の頂点を sのグループ、tのグループに分けたとき、sを含む領域からtを含む領域に流れる有向辺の容量和の最小値を「最小カット」と言います。下図では 5+3+4=12 が最小カットです。

この最小カットは、s から t へ各辺の容量以内で流すことのできるフローの最大値(最大フロー)と一致することが分かっています(最大フロー最小カットの定理と言う)。

もっと詳しく知りたい人は、下記のサイトがとても良いです。「最小カット = 最大フロー」 となる理由についても簡単に記載されています。
燃やす埋める問題とは
A, B, C の3つのもの(ゴミ)を「燃やす」か「埋める」必要がある。
以下の条件下で受け取れる報酬の最大値を求めなさい。
- A, B, C を 「燃やす」 とそれぞれ 50円、100円、130円の報酬が受け取れる。
- A, B, C を 「埋める」 と 90円の報酬が受け取れる。
- B, C を 両方「燃やす」ことは禁止されている(選択肢による依存関係がある)。
<受け取れる報酬>
| もの | A | B | C |
|---|---|---|---|
| 燃やす | 50円 | 100円 | 130円 |
| 埋める | 90円 | 90円 | 90円 |
直感的に、A=埋める、B=埋める、C=燃やす で310円が報酬の最大値になるのは分かりますね。この問題のように、複数の小問題に対して選択肢とコスト・報酬が与えられ、選択肢同士に依存関係があるような問題は、グラフに置き換えて、最大フロー・最小カットを考えると良いです。まずは、選択肢間の依存関係を除いてグラフを考えてみます。カットされる辺が各小問題に対する選択となります。

最小カットは、各辺のコスト最小値を求める考え方になりますので、各選択肢の最大値を基準(無条件でその報酬が受け取れると仮定)にして、各選択肢にコストを設定します。
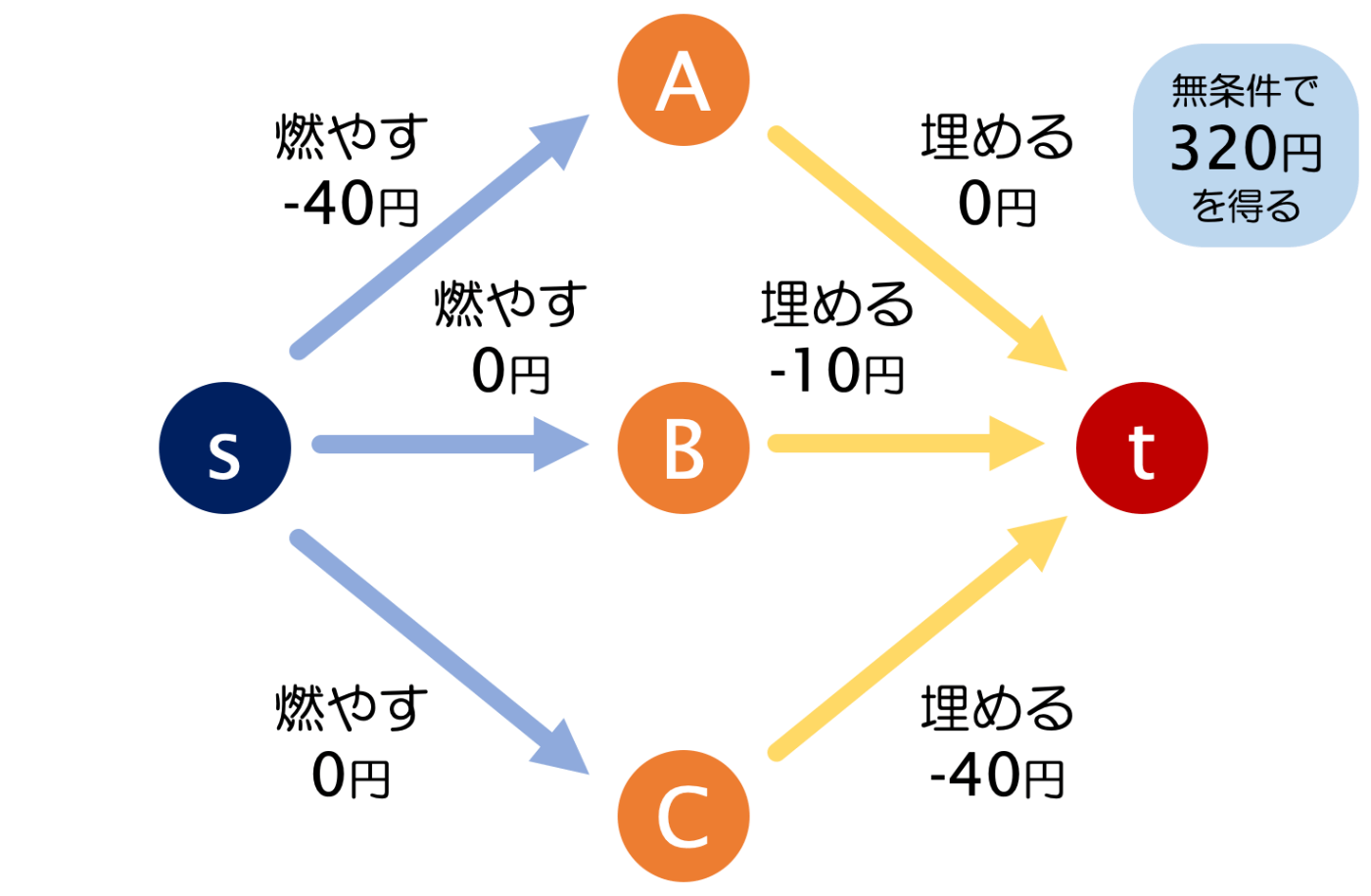
選択肢間の依存関係については、新しくコスト無限大の辺を追加して調整します。B=燃やす、C=燃やす をカットした場合に、コスト無限大の辺をカットしないと、s から t への流れがカットできない(s と t を別グループに分けられない)ようにします。上手くいくように B に出入りする辺の順番を変更しています。

真ん中の無限大の辺があるため、B=燃やす、C=燃やす をカットするだけでは、s から t への流れがカットできません。

最小カットは、{s, A} と {B, C, t} というグループに分けたときですので、無条件で得られる320円から、A=埋める(コスト=0)B=埋める(コスト=10)C=燃やす(コスト=0) として、合計コストの10円を引いた 310円 が最大値となります。

最小カットは最大フローと等しいので、最大フローを求めることができれば最小カットも求めることができます。これで燃やす埋める問題を、最大フローを求める問題に置き換えることができました。

下記のサイトも参考になります。
最大フローを求めるアルゴリズム
最大フローを求める方法としては、
- Fold-Fullkerson法
- Dinic法
が知られています。Dinic法については理解しきれていないので、今回はFold-Fullkerson法を使っていこうと思います。
Ford-Fullkerson(フォード・ファルカーソン)法
アルゴリズムの流れとしては、次の通りです。
- BFS(幅優先探索)で、s(source) から t(sink) へ辿り着くことができるパスを探します。s(source)に近い順に level を記録しておきます。
- 先ほど決定したlevel順に経路をもつパスについて、DFS(深さ優先探索)を行い、フローを流して、残余ネットワークを更新していきます。上階層から下階層へはこれまでの残余ネットワークの最小値を渡していき、一番下の階層から戻ってくるときに、残余ネットワークの更新を行っています。
- 1に戻って、s(source) から t(sink)へ辿り着けるパスを探します。残余ネットワークが更新されているので、t(sink)に辿り着けるパスがもうないかもしれません。仮にパスがなければ終了となります。
残余ネットワークって何? となってしまう人は、上で紹介したサイトで、最大フロー・最小カットについて確認することをオススメします。今回は試しに以下のようなネットワークで、最大フローを計算しようと思います。青字は逆向きのフロー(一度流したフローを戻すという選択肢のために準備します)を表しています。
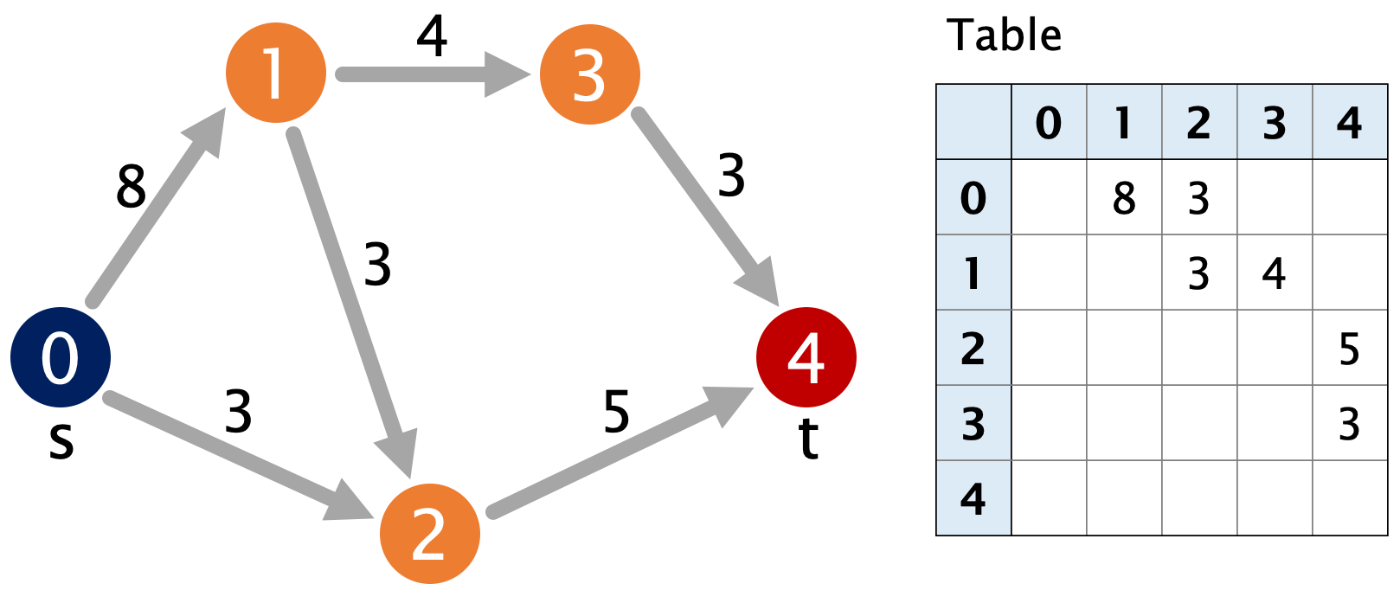
まず始めにBFS(幅優先探索)で、各頂点の level が決まります。
| 頂点 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| level | 0 | 1 | 1 | 2 | 2 |
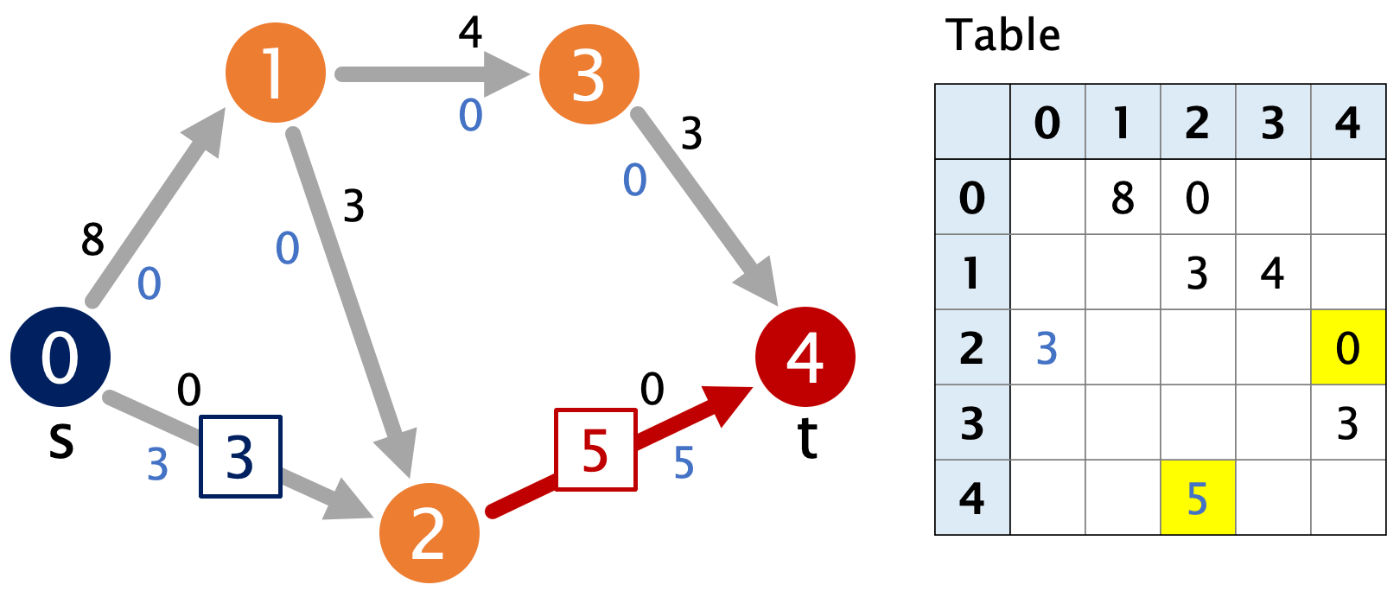
level の序列がある流れ(level 小→大 へ流れる)を考えていきますので、0→2→4 という流れを考えます。深い方から残余ネットワークを更新することになります。DFS(深さ優先探索)を行う際に、上階層からは残余ネットワークの最小値を渡していきますので、0→2 の残余 3 を反映してフローは 3 だけ流れることになります。


もう一度、BFS(幅優先探索)で、各頂点の level を調べます。
| 頂点 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| level | 0 | 1 | 2 | 2 | 3 |
今度は level が変わりました。これは、0→2 への残余ネットワークが 0 になったため、頂点2へは頂点1を介していく必要があります。


一度、頂点0まで戻ってきましたが、0→1→2→4 のパスだけでなく、0→1→3→4 のパスも、level の序列があるパスです。

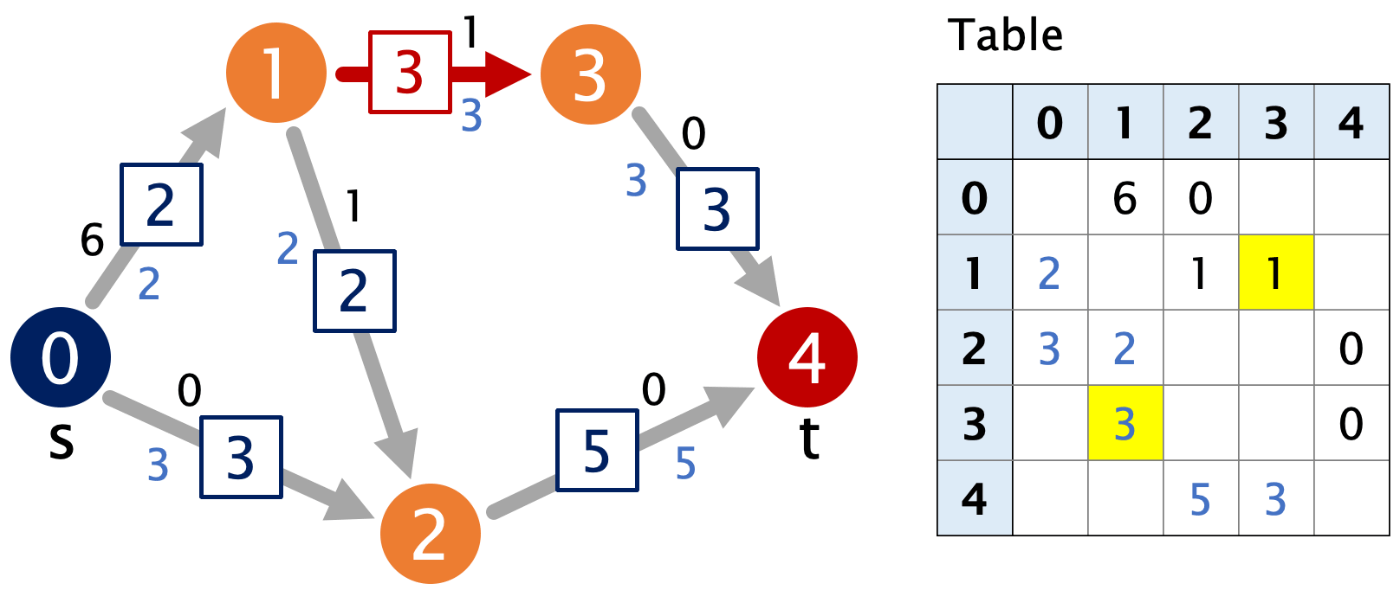

最後に BFS(幅優先探索)で、各頂点の level を調べますが、t (sink) である頂点4へのパスが存在しません。つまり level が -1 のままの場合には、到達不可能と考えこれ以上の更新はできません。
Pythonでの実装
from collections import deque
N = 3; INF = 10**18
# 頂点間ネットワークの初期設定です。
table = [[0,8,3,0,0],[0,0,3,4,0],[0,0,0,0,5],[0,0,0,0,3],[0,0,0,0,0]]
BFS(幅優先探索)で各頂点へ移動可能かどうか、何番目に到達する頂点かを調べます。
def BFS(v):
level[v] = 0
q=deque()
q.append(v)
while q:
v = q.popleft()
for u in range(N+2):
if level[u] < 0 and table[v][u] > 0:
level[u] = level[v] + 1
q.append(u)
DFS(深さ優先探索)では、下階層にフローの大きさを渡していきます。return で返ってくるのは、下位でのフローの最小値となっています。
def DFS(fr,flw):
if fr == N+1:
return flw
for to in range(N+2):
if table[fr][to] > 0 and level[fr] < level[to]:
Dflw = DFS(to,min(flw,table[fr][to]))
if Dflw > 0:
table[fr][to] -= Dflw
table[to][fr] += Dflw
return Dflw
return 0
MaxFlwの初期値を 0 とおいて、まずは level を初期化して、BFS でパスを探します。頂点 4 へのパスが存在するならば、DFS(深さ優先探索)を行い、MaxFlwの値に df=DFS() の計算値を加算します。
MaxFlw = 0
while True:
level = [-1]*(N+2)
BFS(0)
if level[N+1] < 0 : break
while True:
df = DFS(0,INF)
if df > 0:
MaxFlw += df
else:
break
print(MaxFlw)
Dinic(ディニッツ)法
今回用いた Ford-Fullkerson法よりも無駄が少ないようですが、理解できていないので、また別の機会にしたいと思います。
問題演習へ続く
複数の小問題に対して選択肢とコスト・報酬が与えられる問題は、グラフを考えると最小カット・最大フロー問題へ置き換えることができます。Ford-Fullkerson法や、Dinic法を用いれば最大フローを求められるので、問題を解くことができます。長くなってしまったので、問題演習は別記事にします。以下の問題を考えていく予定です。
- ARC085-E問題 MUL
- ABC193-F問題 Zebraness
- 典型90問-040 Get More Money
Discussion