[EDPC-Z問題 Frog 3] Educational DP Contest を Pythonで解く
はじめに
競技プログラミング(使用言語はPython)を日々精進中です。
DP(動的計画法)をマスターするために、AtCoderのEducational DP Contestを解いています。
Z問題 Frog 3
問題概要
制約
考え方
DP[i]は、足場iに到達するまでのコスト最小値と定義して、TLEとなるコードであれば、
N,C=map(int,input().split())
h = list(map(int,input().split()))
INF = 10**18
DP = [INF]*N
DP[0] = 0
for i in range(1,N):
for j in range(i):
DP[i] = min(DP[i], DP[j]+(h[i]-h[j])**2+C)
ans = DP[N-1]
print(ans)
で正しい出力自体は得られます。
ここで、計算のボトルネックとなっているのは下記の部分なので、展開して
minの中を
Convex Hull Trick という傾きが単調減少となる直線群における最小値を求める方法を用います。
これらの直線上での
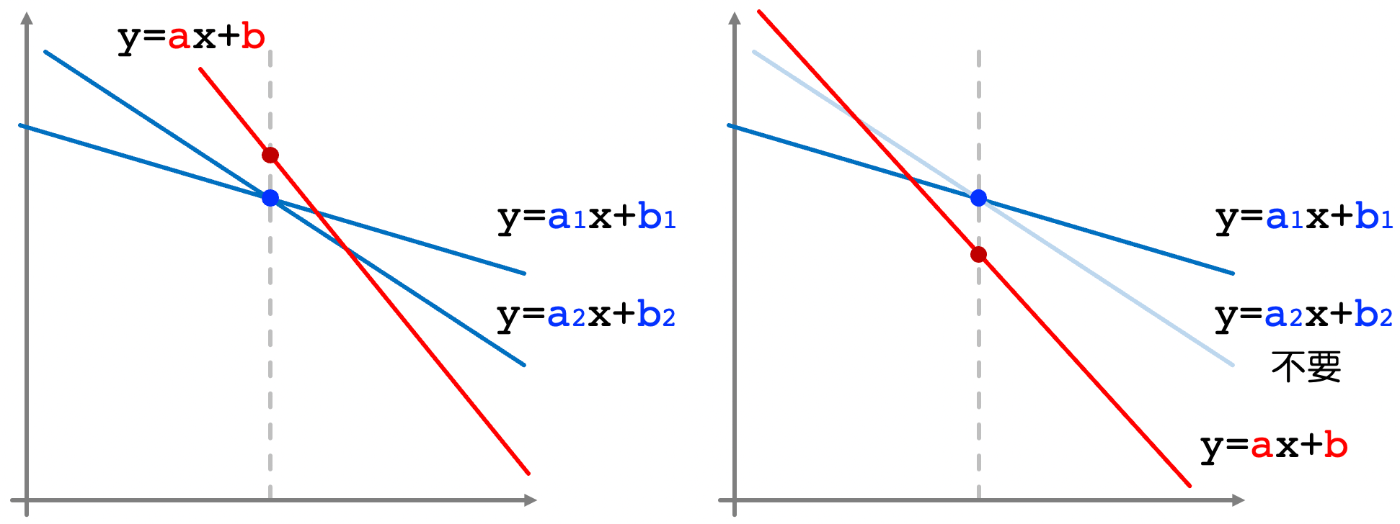
傾き
また、
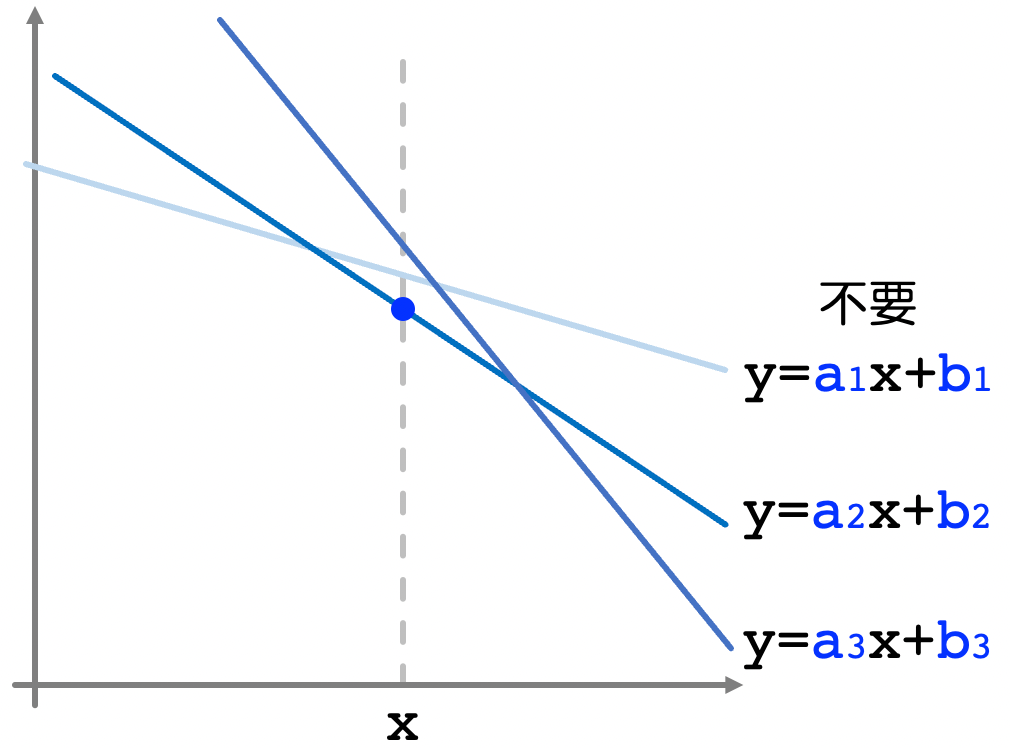
実装メモ
from collections import deque
N,C = map(int,input().split())
h = list(map(int,input().split()))
dp = [0] * N
fs = deque()
def add(i):
hi = h[i]
a,b = -2*hi,hi**2+dp[i]
while len(fs) >= 2:
a1,b1 = fs[-2]
a2,b2 = fs[-1]
if (a2-a1)*(b-b2) < (b2-b1)*(a-a2):
break
fs.pop()
fs.append((a,b))
一番右端の直線を条件を確認して削除する。
def get_min(x):
a1,b1 = fs[0]
y = a1*x+b1
while len(fs) >= 2:
a2,b2 = fs[1]
if y < a2*x+b2:
break
y = a2*x+b2
fs.popleft()
return y
最小値を求める際に必要なければ、一番左端の直線を削除する。
add(0)
for i in range(1,N):
hi = h[i]
dp[i] = get_min(hi) + hi**2 + C
add(i)
ans = dp[-1]
print(ans)



Discussion