はじめに
SpecularのBSDFとして長年使われてきたMicrofacet Modelですが、そのImportance Samplingについては直近だとTokuyoshi氏、Eto氏によるBounded VNDF Sampling for the Smith-GGX BRDF[Tokuyoshi, Eto 2024]が発表されたりとまだまだ研究が進んでいます。
この記事では[Tokuyoshi, Eto 2024]の手法の解説を目指して、先行手法である[Dupuy, Benyoub 2023]の手法から解説していこうと思います。
ここでは論文に準じてZ-up座標系を使用して話すので実装の際は座標系の違いに気を付けてください(y-upならzとyを入れ替えてやればいいはずです)。また、方向\omegaの成分はTangent空間座標で(x,y,z)と書きます。
この記事は可視法線分布関数(VNDF)によるサンプリング VNDF Samplingを知っている方向けの説明になります。これについてあまり知らない方は石山浩平氏、大垣真二氏による物理ベースマテリアルのためのマイクロファセットBRDF入門をお勧めします。
VNDFの定義
VNDF(Visible Normal Distribution Function)の定義は法線分布関数D(\omega_m), 片方向シャドウィングマスキング関数G_1(\omega,\omega_m)によって以下のように定義されています
D_{vis}(\omega_i,\omega_m) = \frac{G_{1}(\omega_i,\omega_m) |\omega_i \cdot \omega_m| D(\omega_m)}{\omega_i \cdot n}
D(\omega) = \frac{1}{\pi \alpha_x \alpha_y(\frac{x^2}{\alpha_x^2} + \frac{y^2}{\alpha_y^2} + z^2)^2}
G_1(\omega,\omega_m) = \frac{1}{1 + \Lambda(\omega)}
\Lambda(\omega) = \frac{-1 + \sqrt{1 + \frac{\alpha_x^2 x^2 + \alpha_y^2 y^2}{z^2}}}{2}
また、一般的なVNDF Samplingは一旦\alpha_x = \alpha_y = 1とした最も単純な状況へと変換するStretchと呼ばれる操作を行います。この状況におけるGGX、片方向シャドウィングマスキング関数をStandard GGXD_{std},Standard G1 G_{1,std}と表記し、VNDFはStandard VNDF D_{vis,std}と表すことにします。
D_{vis,std}(\omega_i,\omega_m) = \frac{G_{1,std}(\omega_i,\omega_m) |\omega_i \cdot \omega_m| D_{std}(\omega_m)}{\omega_i \cdot n}
D_{std}(\omega_m) = \frac{1}{\pi}
G_{1,std}(\omega_i,\omega_m) = \frac{2z_i}{1 + z_i}
分かりづらいので展開した結果をここに示しておきます。
D_{vis,std}(\omega_i,\omega_m) = \frac{2 (\omega_i \cdot \omega_m)}{\pi (1+ z_i)}
Stretch操作について
最近のGGXの手法の多くは先ほど述べたStretch操作によってもっとも単純なStandard GGXの空間へと変換することで問題を簡略化(一般化)しています(VNDF SamplingやLTCなど)。Standard GGXの形を見ればわかるように完全に定数となっているのでLambert的な嬉しさがあるわけですね。
Roughnessが\alpha_x, \alpha_yに対するStretch操作は次のように定義されています。
\omega' = \mathrm{Normalize}(x * \alpha_x,y * \alpha_y,z)
Stretchされた空間はここではStretch空間と呼び、その空間における方向ベクトルは'を付けて表示します。逆にStretch空間からTangent空間に戻すときは次のような変換をします
\omega = \mathrm{Normalize}(x' / \alpha_x,y' / \alpha_y,z')
一方で、空間に対するスケーリング操作に対しては法線はその逆を取らないといけない話があるように、Microfacetの法線\omega_mに関しては逆数を付ける形で変形を行います。
\omega_m' = \mathrm{Normalize}(x_m / \alpha_x,y_m / \alpha_y,z_m)
\omega_m = \mathrm{Normalize}(x_m' * \alpha_x,y_m' * \alpha_y,z_m')
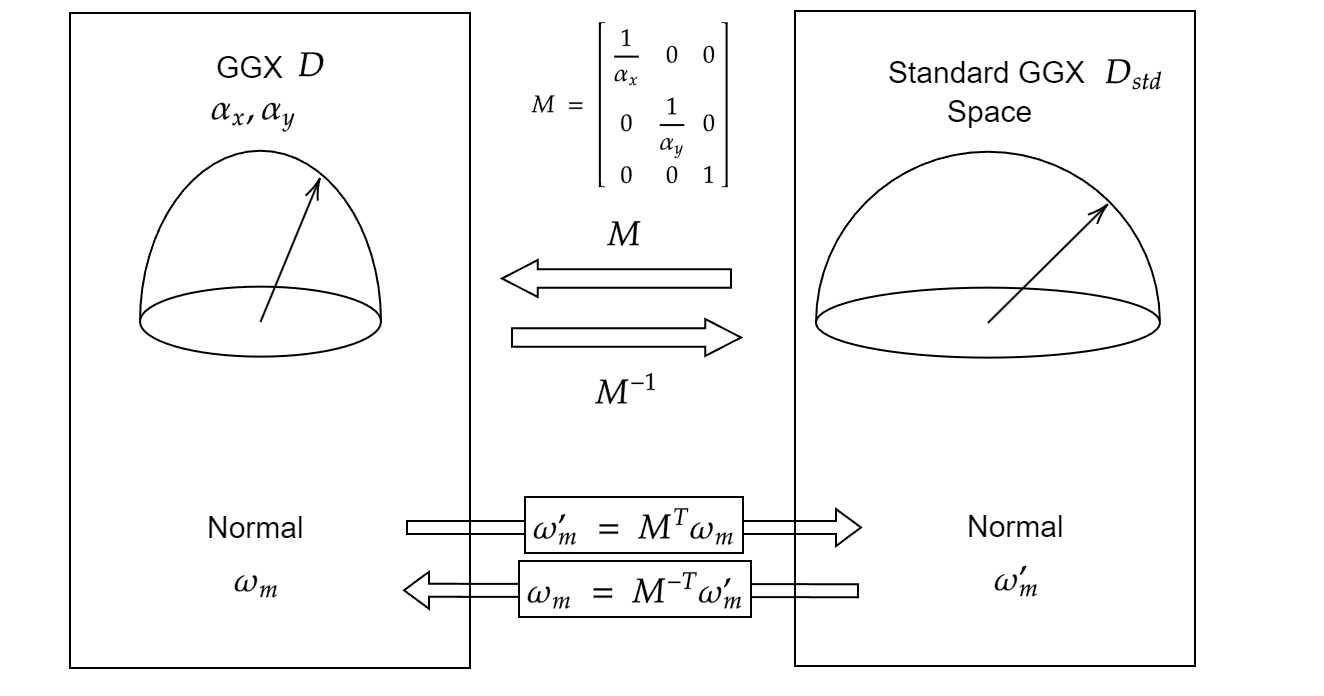
また、より一般化してStandard GGXの空間から特定パラメータのGGX Dに変換する線形変換をMとして、StretchをMによって次のように表記する場合もあります(基準がStandard GGXなのに注意)。
\omega' = \mathrm{Normalize}(M^{-1} \omega)
\omega = \mathrm{Normalize}(M \omega')
\omega_m' = \mathrm{Normalize}(M^{T} \omega_m)
\omega_m = \mathrm{Normalize}(M^{-T} \omega_m')
急にこういう書き方されるとビビりますが、\alpha_x,\alpha_yの時のMは次のように定義されており、代入すればちゃんと同じ式になっていることがわかります(どうもラフネス以外にも変形があったりするので、それを一般化した形式であるみたいです)。
M = \begin{bmatrix}
\frac{1}{\alpha_x} & 0 & 0 \\
0 & \frac{1}{\alpha_y} & 0 \\
0 & 0 & 1
\end{bmatrix}
Stretch空間の法線\omega_m'とTangent空間\omega_mへと変換された時のヤコビアン||\frac{\omega_m'}{\omega_m}||というのはこのMを用いて次のような関係があることが知られています(詳しい導出はAtanasov et al., 2022を参照)
|| \frac{\omega_m'}{\omega_m} || = \frac{\det{M}}{||M\omega_m||^3}
[Dupuy, Benyoub 2023]の手法
Microfacet、特に法線分布関数がGGXである場合効率的なサンプリングが[Heitz 2018]によって発表されていました。これは可視法線分布関数に従って重点的サンプリング(以下VNDF Sampling)するものであり、（一部ではありますが）シャドウマスキング関数が考慮されているため、法線分布関数のみを対象とする[Walter 2008]の手法に比べて効率的であるとされています。
十分実用的ではありましたが、実際のレンダリングはこれを何百、何千回と使うことになるため、軽量化に対するモチベーションはまだまだ健在でした。
これに対して[Dupuy, Benyoub 2023]はVNDF Samplingの効率化に成功しました。この手法の大きな特徴として名前にあるようにSpherical Capという領域を考え、そこでより単純なサンプリングをすることで計算量を減らしています。
この時、得られる反射ベクトル\omega'_o = (x'_o, y'_o, z'_o)の範囲について考えてみます。\omega'_i, \omega'_mの値によっては出射方向\omega'_oはz'_o < 0、簡単に言えばサーフェイスにめり込んでいく方向をとることがあります。z'_oが負になる方向に行くのは物理的にもOKなのでいいのですが、これには限界があります。
\omega'_oは\omega'_mを法線とした\omega'_iの反射ベクトルであるということを念頭に置くと、ある\omega'_iが与えられたとき\omega'_oが一番下の方向へと進む場合というのは\omega'_mが真横(z'_m = 0)を向いているときのはずです。ここでは図で分かるように\omega'_oは\omega'_mを軸として\omega'_iに対称になるため、z'_o = -z'_iが成り立ちます。
そして、これ以上\omega'_oは低い方向へと行くことはできないのでz'_oには最小値として-z'_iが与えられることになります。
この時、\omega_iに対して\omega_oが取れる球面上の領域をSpherical Capと呼びます。
ようやく本題のSpherical Capが出てきました。[Dupuy, Benyoub 2023]はSpherical Capでまず\omega'_oを直接サンプリングし、\omega'_i,\omega'_oのハーフベクトルとして\omega'_mを求めます。
それで如何にサンプリングするかという話なのですが、一応論文の目的としてVNDF Samplingの性質を変えずにやりたいということがあります。したがって、この手法におけるImportance SamplingのPDFはVNDF Samplingと全く同じであるように設計します。
Spherical Cap上で\omega'_oをサンプリングするPDFをf_p(\omega'_o,\omega'_i)とした時、最終的に得られる\omega'_mのPDFをp(\omega'_m,\omega'_i)とします。この時、PDFの変数変換の関係式から次の式が成り立ちます。
f_p(\omega'_o,\omega'_i) = p(\omega'_m,\omega'_i) ||\frac{\omega_m}{\omega_o}||
一番左にある||\frac{\omega'_m}{\omega'_o}||は\omega'_mと\omega'_oのヤコビアンです。これは以下のようになることが既に知られています(導出を知りたかったらogakiさんの資料がわかりやすいです)。
||\frac{\omega'_m}{\omega'_o}|| = \frac{1}{4|\omega'_o \cdot \omega'_m|}
ここで\omega'_iと\omega'_oが\omega'_mを法線とした反射ベクトルの関係にあるため
|\omega'_o \cdot \omega'_m| = |\omega'_i \cdot \omega'_m|
という関係が成り立ちます。
目的を考えればp(\omega'_m,\omega'_i)はVNDF SamplingのPDFになってほしいので目的のf_pについては次のように定義することができます。
f_p(\omega'_o,\omega'_i) = D_{vis,std}(\omega'_i,\omega'_m) \frac{1}{4|\omega'_i \cdot \omega'_m|}
VNDFの定義を代入してあげてまとめていくと、最終的には次のようになります
f_p(\omega'_o,\omega'_i) = \frac{1}{2\pi (1 + z'_i)}
とえられます。これは面白いことにz'_o = [-z'_i,1]の範囲にあるSpherical Capの面積と一致します。
何かしらの一様サンプリングを導出したことがある人ならわかると思いますが、一様サンプリングのPDFはサンプリング領域の面積として定義して、そこから一様サンプリングを導きます。逆を辿ればPDFがサンプリング領域の面積なら、そのサンプリングは一様サンプリングであることがわかります。
すなわち、目的のSpherical Cap上のサンプリングは一様サンプリングであることが導かれます。
よって、この手法は次のような手順でサンプリングを行います。
-
\omega_iをStretchして\omega'_iを取得
-
\omega'_iのz'_iからSpherical Capの下限値を取得
-
\omega'_oをSpherical Capから一様サンプリング
-
\omega'_i,\omega'_oのハーフベクトルとして\omega'_mを得る
-
\omega'_mをUnStretchして\omega_mを得る
なんだか簡単すぎて怖い感じがありますが、これはちゃんとアンバイアスですし[Heitz 2018]の手法と等価なので全くそっくり交換することができます。
[Tokuyoshi, Eto 2024]の手法
Single Scatteringにおいて実装上の都合でサンプルが無駄になるときがあります。それはサーフェイス方向にめり込む、具体的にはz_o < 0となる時です。
サーフェイス方向へと向かう反射光は理論的には1次反射光として出てくることはできず、もう何度か反射して(Multiple Scattering)からでないと取り扱うことができません。Single Scatteringの式として表されているMicrofacet BDSFはこうした光はないものとして扱わざるを得ません。
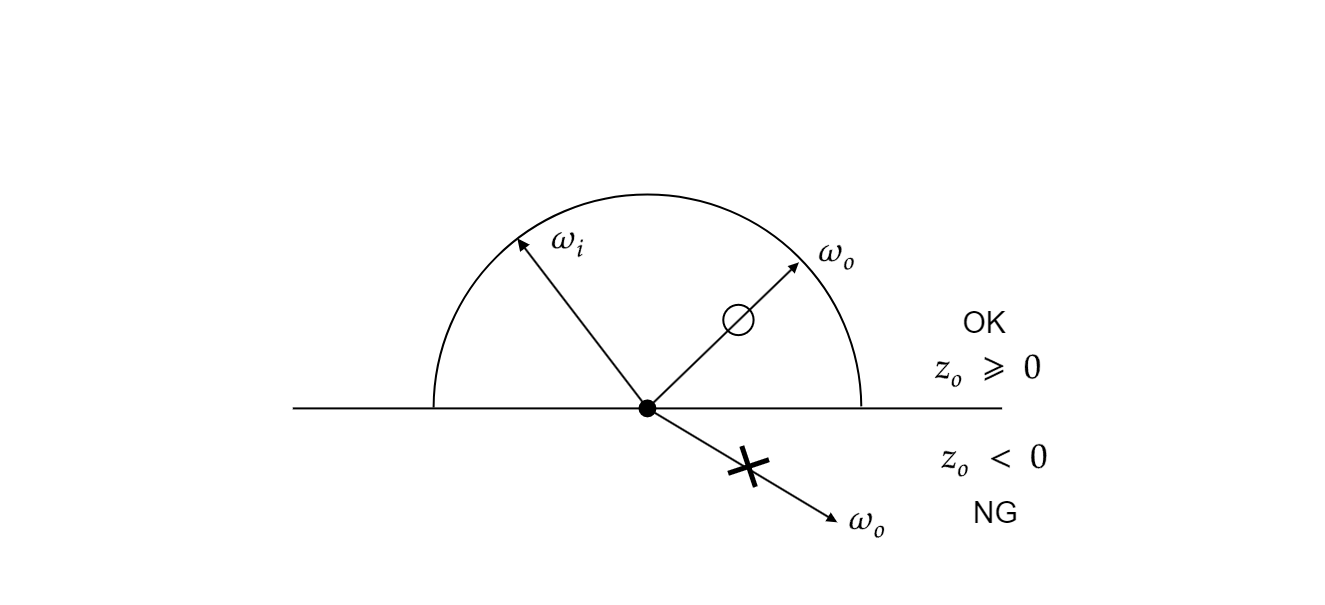
なのでサンプリング時に出射方向ベクトルがz_o < 0であった時、そのサンプルはわざわざ計算したのに棄却する羽目になります(実装上ではそこで計算を打ち切るor再度サンプルを取得するとかしています)
これはGPU実装上でもダイバージェンスの原因にもなり、できる限り減らしておきたいところですが、現状のVNDFサンプリングは一般的なもののためz_o < 0となるサンプルを発生させます(むしろそっちが正しい)。
[Tokuyoshi, Eto 2024]の手法はこうしたz_o < 0のサンプルが出ないようにSpherical Capの下限値をうまく変更してあげるという形で、この問題を回避するというものになっています。どちらかというとSingle Scatteringに対するVNDF Samplingの最適化という立場です。
Spherical Capの下限
「\omega_oのz座標z_oがz_o < 0にならないようなSpherical Capの下限z_{min}を求める」という問題を考えていきます。
まずは\omega_oの偏角\theta,方位角\phiを用いて、\omega'_oと入射方法\omega_iの関係について見ていきます。今回の問題では\thetaは\pi / 2以上の値は取ってほしくない、という目的なので、その境界である\theta = \pi / 2の時のStretch空間における状況というのを考えてみます。
\omega'_oはStretch空間における\omega'_iとは法線を\omega'_mとする反射ベクトルの関係にあるため、反射ベクトルの関係式から
\omega'_o = 2 (\omega'_i \cdot \omega'_m) z'_m - \omega'_i
と求められます。ここで、z成分だけに注目してz'_oを求める式として次のようになります。
z'_o = 2 (\omega'_i \cdot \omega'_m) z'_m - z'_i
ここでStretch変形の関係性から、\omega'_i,\omega'_mは成分的に\omega_i,\omega_mによって書き下すことが可能です。
\omega'_i = \frac{(a_x x_i, a_y y_i, z_i)}{||(a_x x_i, a_y y_i, z_i)||}
\omega'_m = \frac{(x_m / a_m, y_m / a_y, z_m)}{||(x_m / a_m, y_m / a_y, z_m)||}
これを用いて、z'_oは次のようになります。
\begin{aligned}
z'_o &= \frac{2 m_z (a_x x_i, a_y y_i, z_i) \cdot (x_m / a_m, y_m / a_y, z_m)}{||(a_x x_i, a_y y_i, z_i)||||(x_m / a_m, y_m / a_y, z_m)||^2} - i'_z \\
&= \frac{2 m_z (\omega_i \cdot \omega_m)}{||(a_x x_i, a_y y_i, z_i)||||(x_m / a_m, y_m / a_y, z_m)||^2} - i'_z
\end{aligned}
ここで、\omega_oを使用すると\omega_i \cdot \omega_m = ||\omega_i + \omega_o|| / 2、 \omega_m = (\omega_i + \omega_o) / ||\omega_i + \omega_o||の関係から、\omega_mについて消すと
z'_o = \frac{(i_z + o_z) ||\omega_i + \omega_o||^2}{||(a_x x_i, a_y y_i, z_i)||||(\frac{x_i + x_o}{ a_m},\frac{y_i + y_o}{a_y}, z_i + z_o)||^2} - i'_z
と得ることができました。
それで、目的は何だったかというと\theta = \pi / 2の時のz'_oの値を求めたいという話でした。\omega_oは\omega_o = (\cos{\phi},\sin{\phi},0)という形になり、この時のo'_zをo'_z(\frac{\pi}{2},\phi)と表記することにします。これは先ほどの式を使えば、
\begin{aligned}
o'_z(\frac{\pi}{2},\phi) &= \frac{i_z ||\omega_i + \omega_o||^2}{||(a_x x_i, a_y y_i, z_i)||||(\frac{x_i + x_o}{ a_m},\frac{y_i + y_o}{a_y}, z_i)||^2} - i'_z \\
&= \frac{i'_z ||(x_i + \cos{\phi}, y_i + \sin{\phi},z_i))||^2}{||(\frac{x_i + \cos{\phi}}{ a_m},\frac{y_i + \sin{\phi}}{a_y}, z_i)||^2} - i'_z \\
&= \lbrace \frac{(x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2 + z_i^2}{\frac{(x_i + \cos{\phi})^2}{\alpha_x^2} + \frac{(y_i + \sin{\phi})^2}{\alpha_y^2} + z^2_i} - 1 \rbrace i'_z
\end{aligned}
と得ることができました。
この式をぱらっと見るとo'_z(\frac{\pi}{2},\phi)は少なからず\phiに依存することがわかります。それぞれの\phiにおいてo_z > 0が保証される高さというのは異なることがここから導かれます。
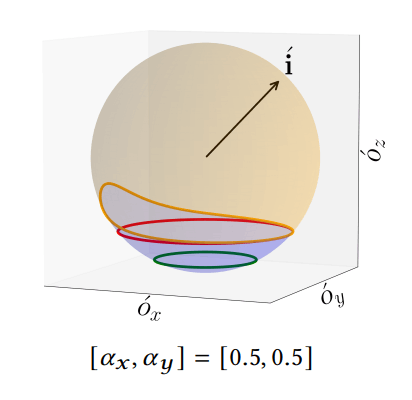
適当なo'_zの最小値を取ってしまっては、ある\phiではo_z > 0のサンプルが一部取れなくなってしまうという問題が生じます。
図で言えば黄色い領域が私たちの欲しいサンプリング領域([o'_z(\frac{\pi}{2},\phi),1])で、Sphereから横にまっすぐ切る感じで私たちは下限を設定したいとしているわけです。黄色い領域は絶対に切ってはいけないため、私たちは黄色い領域の内の一番下の高さで切ってあげる必要があるという感じです。
つまりは、私たちの目的はo'_z(\frac{\pi}{2},\phi)の最小値\min_\phi o'_z(\frac{\pi}{2},\phi_s)を見つけることです。ということです今度はo'_z(\frac{\pi}{2},\phi)を最小にする\phiを見つける問題について考えてみます。
単純化のためIsotropic \alpha_x = \alpha_y = \alphaを仮定して、最小化する\phi(...これを\argmin_{\phi} o'_z(\frac{\pi}{2},\phi)と表記)について求めてみます。
\argmin_{\phi} o'_z(\frac{\pi}{2},\phi) = \lbrace \alpha^2 \frac{(x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2 + z_i^2}{(x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2 + \alpha^2 z_i^2} - 1 \rbrace i'_z
今の目的に従うと、第一項目が最も低くなる状況というのが求める条件です。第一項目の分母と分子は(x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2という値が共通しており、その差は\alpha^2 z_i^2の分だけしかありません。\alpha < 1の時、分母は分子より少しだけ小さくなります。
この関係から、
-
(x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2が小さい→一項目は大きくなる
-
(x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2が大きい→一項目は小さくなる
従って、第一項目を最小化する条件としてr(\phi) = (x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2を最大化するphiを見つければいいことになります。(ややこしいですね)
\argmin_{\phi} o'_z(\frac{\pi}{2},\phi) = \argmax_{\phi} r(\phi)
r(\phi) = (x_i + \cos{\phi})^2 + (y_i + \sin{\phi})^2
(論文では一応\alpha > 1の状況も考えていますが、ここでは省いています)
それで、r(\phi)というのは幾何的に表すと単位円内の点(-x_i,-y_i)と円上点(\cos{\phi}, \sin{\phi})の距離に相当します。この距離が最大となるのは単純に考えて、(-x_i,-y_i)の対角線上にある状況であり、その距離は1 + \sqrt{i_x^2 + i_y^2}であるはずです。この時の解を\phi_sとして、その時の距離をsとしましょう。
s = 1 + \sqrt{i_x^2 + i_y^2}
r(\phi_s) = s^2 = (1 + \sqrt{i_x^2 + i_y^2})^2
こうして、r(\phi)の最大値r(\phi_s)について求められました。この時におけるo'_z(\frac{\pi}{2},\phi_s)が我々が求めたかった最小値\min_\phi o'_z(\frac{\pi}{2},\phi_s)となるわけです(記号がややこしくなってきましたね・・・)。
\begin{aligned}
\min_\phi o'_z(\frac{\pi}{2},\phi_s) &= o'_z(\frac{\pi}{2},\phi_s)\\
&= (\frac{\alpha^2 (s^2 + z_i^2)}{s^2 + \alpha^2 z_i^2} - 1) z'_i \\
&= \frac{(\alpha^2 - 1) s^2}{s^2 + \alpha^2 z_i^2} z'_i
\end{aligned}
ちょっと記号がややこしいので係数部分をkと置き、最終的に
\min_\phi o'_z(\frac{\pi}{2},\phi_s) = -kz'_i, \space k = \frac{(1-\alpha^2) s^2}{s^2 + \alpha^2 z_i^2}
と書くことができます。ようやく目的の値を得ることができました。今回の手法はこれを下限としたSpherical Cap Samplingを行うことで、より効率的なサンプリングを行います。
ちなみにkは実際計算してみるとk<1であるため、[Dupuy, Benyoub 2023]の下限-z_iより大きく、[-z_i,-k z_i]の間にあるサンプルは(SingleScatteringで)不要であることが式からもわかります。
論文中の図を見ると、[Dupuy, Benyoub 2023]の下限は青い線、今回求めた下限は赤い線で表されています。こうしてみると(特にRoughnessが高い時)かなりのサンプルが不要で、[Tokuyoshi, Eto 2024]の下限は結構な最適化がされていることがわかりますね。
Anistropic
今まではIsotropicを前提にしていましたが、Anistropicの場合はどうなるかという話になります。これは単純な話で、より小さい方のRoughnessの下限を使用します。
\alpha = \min(\alpha_x,\alpha_y,1)
\min_\phi o'_z(\frac{\pi}{2},\phi_s)についてはRouhgness\alphaが小さいほど、それに伴って小さくなります。サンプルが取られることを保証するにはより小さい方の下限を取る必要があるため、このような形になっているというわけです。
PDF
[Eto, Tokuyoshi 2024]の手法では今までのVNDF Samplingとは等価ではないサンプリングを行っているため、専用のPDFが必要です。Bound VNDF SamplingのPDFをp_{bound}とした時、Spherical CapのSamplingのPDF p_{sc}から次のように求めることができます。
p_{bound}(\omega_m) = p_{sc}(\omega'_o)||\frac{\omega'o}{\omega'_m}|| ||\frac{\omega'_m}{\omega_m}||
これはサンプルの変換の仕方が\omega'_o \rightarrow \omega'_m \rightarrow \omega_mだからですね。各変換はヤコビアンという関係で結びついています。
p_{sc}については下限-kz'_iのSpherical Capから一様サンプリングするということなので、シンプルに(1/Spherical Capの面積)に相当するので次のように求められます。
p_{sc}(\omega'_o) = \frac{1}{2\pi(1 + k z'_i)}
そして、各ヤコビアンについては既に知っているので、そのまま展開してあげれば次のように求められます。
\begin{aligned}
||\frac{\omega'o}{\omega'_m}|| ||\frac{\omega'_m}{\omega_m}|| &= 4 |\omega'_i \cdot \omega'_m| \frac{1}{\alpha_x \alpha_y (\frac{x_m^2}{a_x^2} + \frac{y_m^2}{a_y^2} + z_m^2)^{\frac{3}{2}}} \\
&= \frac{4 |\omega_i \cdot \omega_m|}{\alpha_x \alpha_y (\frac{x_m^2}{a_x^2} + \frac{y_m^2}{a_y^2} + z_m^2)^2 \sqrt{\alpha_x^2 x_i^2 + \alpha_y^2 y_i^2 + z_i^2}}
\end{aligned}
これをまとめて、法線分布関数と一致する部分をまとめてしまえば最終的に次のように求められます(Stretch座標->Tangent座標の変換に注意)
\begin{aligned}
p_{bound}(\omega_m) &= \frac{1}{2\pi(1 + k z'_i)} \frac{4 |\omega_i \cdot \omega_m|}{\alpha_x \alpha_y (\frac{x_m^2}{a_x^2} + \frac{y_m^2}{a_y^2} + z_m^2)^2 \sqrt{\alpha_x^2 x_i^2 + \alpha_y^2 y_i^2 + z_i^2}} \\
&= \frac{2 D(\omega_m) |\omega_i \cdot \omega_m|}{k z_i + \sqrt{\alpha_x^2 x_i^2 + \alpha_y^2 y_i^2 + z_i^2}}
\end{aligned}
アルゴリズム
以上をまとめてアルゴリズムは次のような手順で行うことができます
-
\omega_iをStretchして\omega'_iへ
-
\omega'_iとRoughnessから下限値の係数kを算出
-
[-kz'_i, 1]のSpherical Capで一様サンプリングして\omega_o'を求める
-
\omega'_i,\omega'_oのハーフベクトルとして\omega'_mを得る
-
\omega'_mをUnStretchして\omega_mを得る
下限値の係数
k = \frac{(1-\alpha^2) s^2}{s^2 + \alpha^2 z_i^2}
PDF
p_{bound}(\omega_m) = \frac{2 D(\omega_m) |\omega_i \cdot \omega_m|}{k z_i + \sqrt{\alpha_x^2 x_i^2 + \alpha_y^2 y_i^2 + z_i^2}}
Limitation
この手法の注意点としては以下のことが挙げられます
- Single Scatteringのみに使用可能
- 完全にz_o < 0のサンプルを取り除けない
- 特にAnisotropicが強い場合、取り除けないz_o < 0のサンプリング領域が増えていく
実装&検証
～後日実装&検証します～
終わりに
前々から知っていて気になってはいたのですが、理論的な部分についての内容がわかっていないまま「どっかのタイミングでちゃんと見たいな～」と思いながら長いこと経ってしまいました。最近、Visual Computing 2024で著者の方が直々に発表してくださり、直接お話を聞きましてようやく手法の核心をつかむことができました（ありがとうございました）。今回の記事はそれをきっかけにとりあえず勢いでまとめたものです。
わかってみるとSpherical Cap VNDF Samplingはとてもエレガントで理論的にもシンプルな手法でかなり驚きました。VNDF Samplingというと幾何的な変換がなかなかつかみづらいという所があったのですが、今回紹介した手法2つは非常に計算がわかりやすく、久しく気持ちいい～という気分になりました。
[Tokuyoshi, Eto 2024]の手法は中々にシンプルで強く、オフラインだけでなくリアルタイム方向の応用も期待しています(実際 BlenderのNext-Eeveeに採用されたみたいです)。Screen Space Reflectionとかのサンプリングに使っても面白そうと感じます。
参考資料
[Tokuyoshi, Eto 2024] Bounded VNDF Sampling for Smith–GGX BRDF
[Dupuy, Benyoub 2023] Sampling Visible GGX Normals with Spherical Caps
[Heitz 2018] Sampling the GGX Distribution of Visible Normals
[Atanasov et al. 2022]Microsurface Transformations
石山 浩平 大垣 真二
物理ベースマテリアルのためのマイクロファセットBRDF入門～リアルな光表現の本質～, CEDEC2023
Proof of the Sampling Method for Visible GGX
Discussion