muP(mu Transfer)でスケールしていく
μPとμTransfer – ハイパーパラメータ転移の革新とその未来
大規模なディープラーニングモデルの学習では、モデルサイズが大きくなるにつれてハイパーパラメータ(HP)の最適設定が変動し、調整コストが急増するという課題があります。
本記事では、Maximal Update Parametrization (μP) とその拡張である Unit-Scaled μP (u-μP) の理論と実践について、数式や図を交えながら詳しく解説します。
さらに、これらの手法がどのように小規模モデルで得た最適HPを大規模モデルにゼロショット転移(μTransfer)できるか、その革新性と今後の可能性についても紹介します
目次
- 研究の概要
- 背景: モデルスケーリングとハイパーパラメータ調整の課題
- μPの理論的基盤と数理解説
- ゼロショット転移 (μTransfer) の実現
- 評価結果と実験的検証
- Unit-Scaled μP (u-μP) の進化
- まとめと今後の展望
- 参考リンク・関連記事
1. 研究の概要
大規模モデルの学習では、従来、各モデルサイズごとに最適な HP を改めて探す必要がありました。
μP (Maximal Update Parametrization) は、ネットワークのパラメータ化を再設計することで、
小規模モデルで調整した HP をそのまま大規模モデルに転移(μTransfer)できるという、画期的なアプローチです。
- 論文例:
- 実装例:
2. 背景: モデルスケーリングとハイパーパラメータ調整の課題
ディープラーニングでは、モデルの幅(ニューロン数)が増加すると、各層の出力や勾配のスケールが変動します。
たとえば、全結合層の初期化では次のような分布がよく用いられます。
ここで
この設定では、モデルサイズの拡大に伴い出力分散が変わるため、最適な学習率
大規模モデルでは個別のHP調整が不可避となり、計算資源と時間が大幅に消費されていました。
3. μPの理論的基盤と数理解説
3.1 μP の基本アイデア
μP の核心は、パラメータの再パラメータ化にあります。
具体的には、重み行列
ここで、
-
\hat{W} -
\mu
この分解により、学習中の更新は次のように表現されます。
これにより、各層の出力や勾配がモデルサイズに依存せず、常に同一スケールを維持できるようになります。
その結果、最適な学習率 $ \eta $ やその他の HP がモデルサイズに関わらずほぼ一定に保たれ、
小規模モデルで得た最適設定を大規模モデルへそのまま転移できるのです。
3.2 理論的背景
μP の設計は、無限幅ニューラルネットワークの振る舞いを解析するTensor Programs理論に基づいています。
この理論は、ネットワークが無限幅に近づくとき、各層の出力や勾配がどのような確率分布に収束するかを厳密に解析し、
従来の経験的アプローチでは捉えきれなかったスケーリング則を導き出しました。
4. ゼロショット転移 (μTransfer) の実現
μP の革新性は、小規模モデルで調整した HP を大規模モデルにそのまま転移できる点にあります。
従来、例えば大規模な GPT-3 や BERT モデルでは、モデルサイズごとに最適な学習率や正則化パラメータを再設定する必要がありました。
しかし、μP を用いることで以下のメリットが得られます。
-
計算コストの大幅削減
小規模モデルでの調整結果をそのまま大規模モデルに適用可能なため、個別の再調整が不要。 -
再現性の向上
モデルサイズに依存しない HP 設定により、同一の設定で複数サイズのモデルを比較可能。
図 1: 標準的なパラメータ設定 vs μP
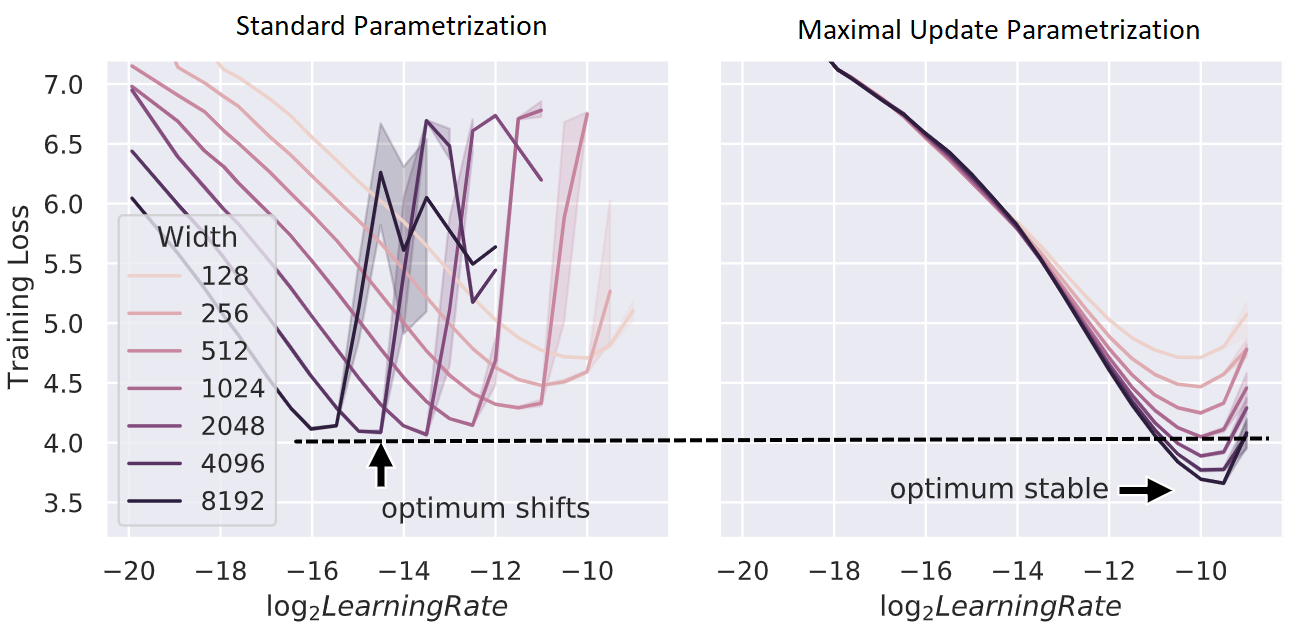
左:従来の設定ではモデルサイズにより最適学習率が変動。右:μPではサイズに依存せず安定。
5. 評価結果と実験的検証
実験結果から、μP の有効性は次のように実証されています。
-
Transformer 系モデル
小型 Transformer で調整した HP を BERT-Large に転移することで、従来の個別チューニングと同等または上回る性能を実現。 -
大規模モデルへの応用
約 40M パラメータの小型モデルで最適化した設定を 6.7B パラメータの大規模モデルに適用し、学習全体の計算コストを大幅に削減(わずか約 7% のコスト)しながら高い精度を達成。 -
広範なスケーリング実験
Transformer の隠れ層幅を 128 から 8192 まで拡大しても、最適学習率 $ \eta $ がほぼ一定に保たれることが確認されています。
これらの結果は、μP による HP 転移が大規模モデルの開発効率と再現性を劇的に向上させることを示しています。
6. Unit-Scaled μP (u-μP) の進化
2024 年に提案された Unit-Scaled μP (u-μP) は、μP の概念をさらに発展させたものです。
u-μP は、全ての重み・活性値・勾配を初期からユニットスケール(すなわち
特に低精度演算(FP16、FP8 など)環境下での学習の安定性を向上させます。
具体的には、各層の重みは次のように初期化されます。
この手法により、初期状態から各パラメータのスケールが統一され、
演算時のオーバーフローやアンダーフローのリスクが低減。
結果として、u-μP は特別な調整を必要とせずに低精度環境下でも安定した学習が可能となります。
- 参考実装:
7. まとめと今後の展望
μP とその発展形である u-μP は、「小規模モデルで得た最適なハイパーパラメータをそのまま大規模モデルに転移できる」
というこれまでのスケーリングの壁を打破する画期的な手法です。
これにより、
- 大規模モデルのチューニングに要する計算リソースが大幅に削減され、
- 安定した再現性の高い学習が実現、
- 低精度計算環境下でも高いパフォーマンスが期待できる
といったメリットがもたらされます。
今後、これらの技術が標準的な機械学習フレームワークに組み込まれ、さらなる発展を遂げることが予想されます。
8. 参考リンク・関連記事
- 関連論文:
- 実装リポジトリ:
- 関連記事:
この分野は急速に進化しており、今回ご紹介した μP と u-μP もその一端に過ぎません。
さらに詳しい理論背景や実装の詳細、そして新たな実験結果については、他の記事でも豊富に取り上げています。
ぜひ、あなたの知識をさらに深めるために、他の関連記事もご覧ください!
次回も最新の研究動向を追いかけ、一緒にディープラーニングの未来を探求していきましょう。
Discussion