「犬と同居している人はiPhone派、猫と同居している人はAndroid派」は本当か？ 統計的検定してみた

ネタバレ: ちゃんと有意差が出ました。

概要

このような記事 犬と暮らす人はiPhoneが多く、猫はAndroidスマホが多い を見かけました。本当かしら。
https://www.itmedia.co.jp/news/articles/2309/15/news068.html
たまたま差があるように見えただけなのか、統計的にも有意差が出せるのかが気になり、統計的検定をしてみました。

ちなみに自分はiPhoneユーザーで猫派ですが、猫は飼っていません。

データの前処理

出典元はモバイル社会研究所のレポートです。こちらに実際の値のcsvが公開されていました。
https://www.moba-ken.jp/project/lifestyle/20230914.html

割合しか載っていない部分もあったので、N数を逆算しました。
公開データが小数点1桁未満を丸めているので実際のN数とは少しズレると思いますが、大勢には影響ないと思います。

性別	年代	犬猫同居無	犬のみ	猫のみ	犬と猫
男	15-39歳	1,081	64	65	17
男	40-59歳	1,063	107	66	18
男	60-79歳	949	93	60	7
女	15-39歳	999	74	82	18
女	40-59歳	1,012	100	90	20
女	60-79歳	1,019	76	82	6
	合計	6,123	514	445	86

[実測値]	犬猫同居無	犬のみ	猫のみ	犬と猫	合計
iPhone＆Android	141	10	11	9	171
iPhoneのみ	2,590	258	181	41	3,070
Androidのみ	2,915	226	230	34	3,405
その他	484	20	24	2	530
合計	6,123	514	445	86	7,168

• 計算に用いたスプレッドシート

統計的検定

「iPhone派かAndroid派か」と「犬と同居するか猫と同居するか」の傾向に関連があるかどうかを検定します。
帰無仮説「両者は独立である（関連がない）」を仮定した上で、カイ二乗統計量を計算します。

そのために、「期待値」テーブルを作ります。これは、「両者に関連がないとしたら人数の分布はこうなっているだろう」という値で、例えば iPhoneのみ×犬猫同居無 の人数の期待値は

$$\begin{align*} &(\mathrm{iPhoneのみの合計人数}) \times (\mathrm{全体の犬猫同居無率})\\ &~=~ (\mathrm{iPhoneのみの合計人数}) \times (\mathrm{犬猫同居無の合計人数} / \mathrm{全体人数}) \\ &~=~ (\mathrm{犬猫同居無の合計人数}) \times (\mathrm{iPhoneのみの合計人数}) \times / \mathrm{全体人数} \end{align*}$$

となります。スプシで計算する際は、期待値テーブル全部を1つの式でスッキリと書くことができます。まだやったことのない方は自分で式を書いてみることをオススメします。

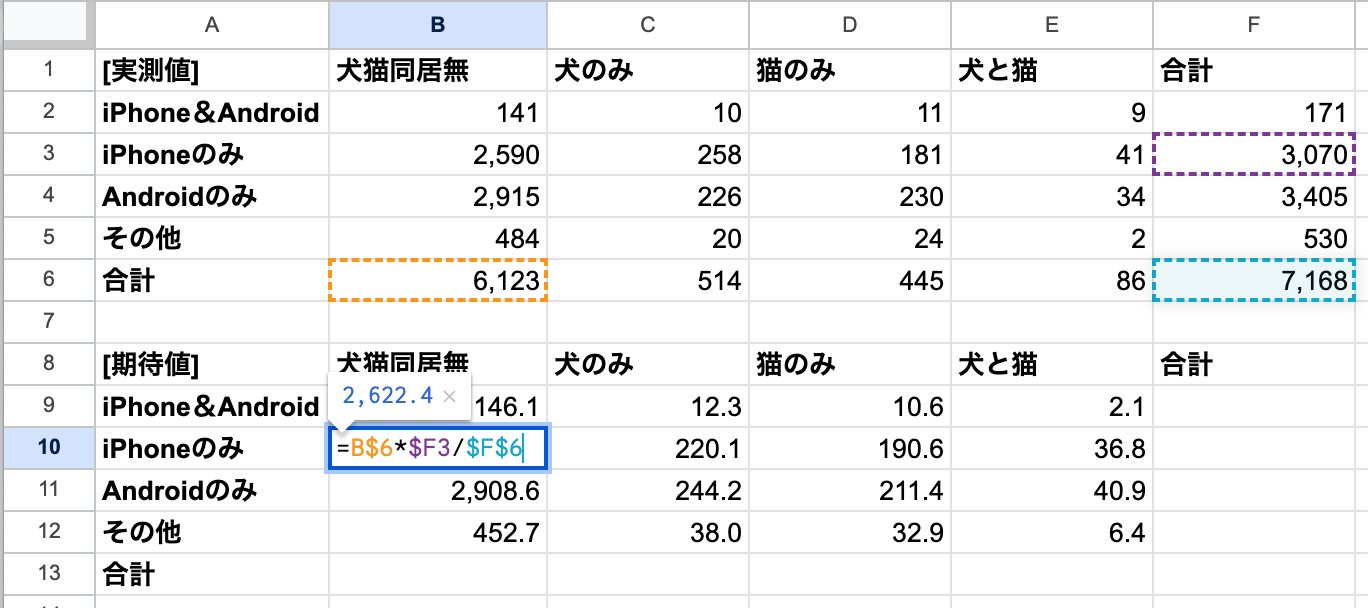
あとはスプシ（or Excel）の関数である CHISQ.TEST を使えばp値が出せます。第1引数が実測値テーブル、第2引数が期待値テーブルです。

この場合の p値 = 0.000000041 だったので、（有意水準5%だろうと1%だろうと）有意差があるといえます。

結論

「iPhone派かAndroid派か」と「犬と同居するか猫と同居するか」の傾向には関連があるといえます。