🌈
そろそろShaderをやるパート58 行列を理解する(拡大縮小編)
そろそろShaderをやります
そろそろShaderをやります。そろそろShaderをやりたいからです。
パート100までダラダラ頑張ります。10年かかってもいいのでやります。
100記事分くらい学べば私レベルの初心者でもまあまあ理解できるかなと思っています。
という感じでやってます。
※初心者がメモレベルで記録するので
技術記事としてはお力になれないかもしれません。
下準備
下記参考
そろそろShaderをやるパート1 Unite 2017の動画を見る(基礎知識~フラグメントシェーダーで色を変える)
デモ
頂点シェーダーを行列の計算式で拡大縮小させています。
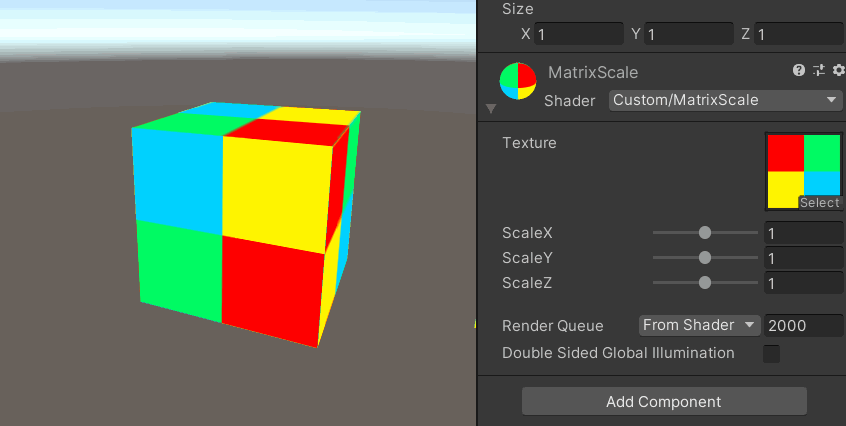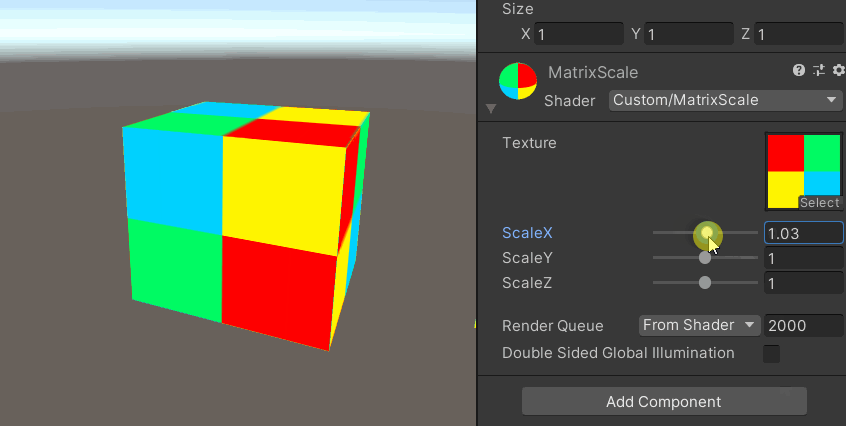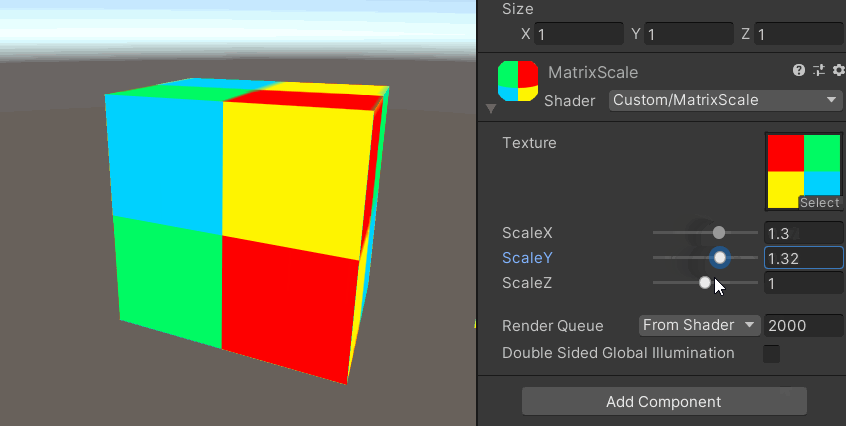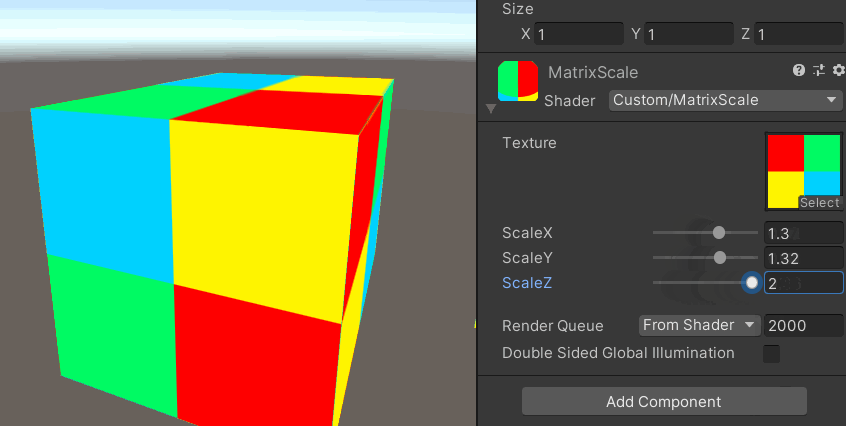
行列の旨味の理解は下記記事でまとめました。
【参考リンク】:そろそろShaderをやるパート56 行列を理解する(平行移動編)
拡大縮小の理屈
まずは2次元座標における拡大縮小の理屈を考えます。
座標P(x,y)をSx倍、Sy倍させ、座標Q(x',y')に移動させることで拡大が実現できます。
縮小は倍率を1以下にすれば成り立ちます。
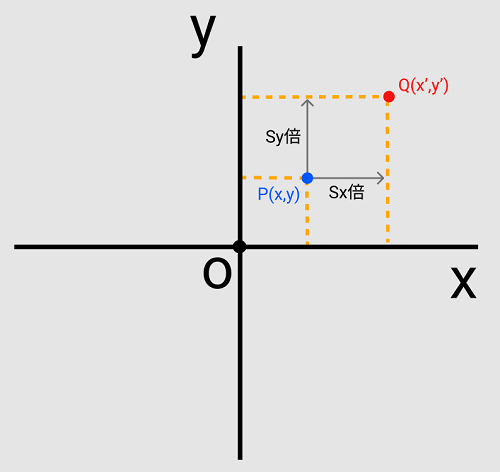
これを連立方程式に表すと下記です。
行列に変換すると以下のようになります。
これも前回記事同様に同時座標系で扱い、
アフィン変換のメリットを受けやすい形へ変換します。
これで完成です。あとはこの変換を三次元で取り扱います。
Shaderサンプル
Shader "Custom/MatrixScale"
{
Properties
{
[NoScaleOffset]_MainTex ("Texture", 2D) = "white" {}
_ScaleX("ScaleX",Range(0,2)) = 1
_ScaleY("ScaleY",Range(0,2)) = 1
_ScaleZ("ScaleZ",Range(0,2)) = 1
}
SubShader
{
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
};
sampler2D _MainTex;
float _ScaleX;
float _ScaleY;
float _ScaleZ;
v2f vert(appdata v)
{
v2f o;
//スケールのための行列を計算
half4x4 scaleMatrix = half4x4(_ScaleX, 0, 0, 0,
0, _ScaleY, 0, 0,
0, 0, _ScaleZ, 0,
0, 0, 0, 1);
v.vertex = mul(scaleMatrix, v.vertex);
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
return o;
}
fixed4 frag(v2f i) : SV_Target
{
//テクスチャーのサンプリング
fixed4 tex_color = tex2D(_MainTex, i.uv);
return tex_color;
}
ENDCG
}
}
}
アフィン変換を1つのShaderに
過去記事で平行移動と回転を学んだので、
今回の記事の拡大縮小と合わせて1つのShaderにまとめてみました。

Shaderサンプル
Shader "Custom/MatrixMix"
{
Properties
{
//メインテクスチャー
[NoScaleOffset]_MainTex ("Texture", 2D) = "white" {}
//キーワードのEnumを定義できる なぜか変数名が大文字でないと変更が反映されなかった
[KeywordEnum(X,Y,Z)] _AXIS("Axis",Int) = 0
_Rotation("Rotation",Range(-6.28,6.28)) = 0
_ScaleX("ScaleX",Range(0,2)) = 1
_ScaleY("ScaleY",Range(0,2)) = 1
_ScaleZ("ScaleZ",Range(0,2)) = 1
_MoveX("MoveX",Range(-0.5,0.5)) = 0
_MoveY("MoveY",Range(-0.5,0.5)) = 0
_MoveZ("MoveZ",Range(-0.5,0.5)) = 0
}
SubShader
{
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
//ここでシェーダーキーワードを定義する
#pragma multi_compile _AXIS_X _AXIS_Y _AXIS_Z
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
};
sampler2D _MainTex;
float _Rotation;
float _MoveX;
float _MoveY;
float _MoveZ;
float _ScaleX;
float _ScaleY;
float _ScaleZ;
v2f vert(appdata v)
{
v2f o;
// 回転行列を作る
half c = cos(_Rotation);
half s = sin(_Rotation);
half4x4 rotateMatrix = half4x4(1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1);
#ifdef _AXIS_X
//X軸中心の回転
rotateMatrix = half4x4(1, 0, 0, 0,
0, c, -s, 0,
0, s, c, 0,
0, 0, 0, 1);
#elif _AXIS_Y
//Y軸中心の回転
rotateMatrix = half4x4(c, 0, s, 0,
0, 1, 0, 0,
-s, 0, c, 0,
0, 0, 0, 1);
#elif _AXIS_Z
//Z軸中心の回転
rotateMatrix = half4x4(c, -s, 0, 0,
s, c, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1);
#endif
//スケールのための行列を計算
half4x4 scaleMatrix = half4x4(_ScaleX, 0, 0, 0,
0, _ScaleY, 0, 0,
0, 0, _ScaleZ, 0,
0, 0, 0, 1);
//移動のための行列を計算
half4x4 moveMatrix = half4x4(1, 0, 0, _MoveX,
0, 1, 0, _MoveY,
0, 0, 1, _MoveZ,
0, 0, 0, 1);
//平行移動、回転、拡大縮小の行列を一気に計算
v.vertex = mul(rotateMatrix, mul(scaleMatrix, mul(moveMatrix, v.vertex)));
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
return o;
}
fixed4 frag(v2f i) : SV_Target
{
//テクスチャーのサンプリング
fixed4 tex_color = tex2D(_MainTex, i.uv);
return tex_color;
}
ENDCG
}
}
}
Discussion