Zenn
🍇

関係データベースにおける集合論

に公開
SQL
DB
RDB
tech

この記事の内容

SQL は集合指向言語。集合論の観点でまとめる。

参考

http://shoeisha.co.jp/book/detail/9784798157825

1. 関係とは集合である

関係の定義（次式）より、関係は、列の定義域の直積の部分集合である。

関係: R , 属性（列）: A_i , その定義域: D_i

R \subseteq D_1 \times D_2 \times D_3 \times \cdots \times D_n

ex.

属性 a_1, a_2, a_3 がそれぞれ次の定義域を取るとする。

d_1 = \{1\}, d_2 = \{'\mathrm{m}', '\mathrm{f}'\}, d_3 = \{'\mathrm{r}', '\mathrm{g}', '\mathrm{b}'\}

このとき、直積は次の通り。

a_1 a_2 a_3
1 m r
1 m g
1 m b
1 f r
1 f g
1 f b

関係（テーブル）は、この部分集合となる。

2. 関係と代数構造

関係（テーブル）は、群であり、環であり、体である。

  • 群: 加法・減法について閉じている
  • 環: 加法・減法・乗法について閉じている
  • 体: 加法・減法・乗法・除法について閉じている

つまり、テーブル同士を足し算、引き算、掛け算、割り算しても、その結果はテーブルである。

ex.

加法、減法、乗法について、次のテーブルに対するクエリを例示する。

A テーブル
id name
1 太郎
2 花子
3 次郎
B テーブル
id name
1 太郎
2 花子
4 三郎

2.1 加法（UNION）

SELECT name FROM A
UNION
SELECT name FROM B;
結果
name
太郎
花子
次郎
三郎

2.2 減法（EXCEPT）

SELECT name FROM A
EXCEPT
SELECT name FROM B;
結果
name
次郎

2.3 乗法（CROSS JOIN）

SELECT
  A.name AS a_name,
  B.name AS b_name
FROM
  A CROSS JOIN B;
結果
a_name b_name
太郎 太郎
太郎 花子
太郎 三郎
花子 太郎
花子 花子
花子 三郎
次郎 太郎
次郎 花子
次郎 三郎

2.4 除法

演算子は定義されていないが、次の 3 通りで表現できる。

  • NOT EXISTS を入れ子にする
  • HAVING 句を使う
  • 減法で表現する

ex.

EmployeeSkill テーブルから、RequiredSkill テーブルの技術すべてに精通した社員を選択する。

RequiredSkill テーブル
skill
Oracle
UNIX
Java
EmployeeSkill テーブル
emp_id skill
1 Oracle
1 UNIX
1 Java
1 C#
2 Oracle
2 UNIX
2 Java
3 UNIX
3 Oracle
3 PHP
3 Perl
3 C++
4 Perl
5 Oracle
結果
emp_id
1
2

2.4.1 NOT EXISTS を入れ子にする

SELECT emp_id
FROM EmployeeSkill ES1
WHERE NOT EXISTS (
    SELECT skill
    FROM RequiredSkill RS
    WHERE NOT EXISTS (
        SELECT 1
        FROM EmployeeSkill ES2
        WHERE ES2.emp_id = ES1.emp_id
          AND ES2.skill = RS.skill
      )
  );

2.4.2 HAVING 句を使う

SELECT emp_id
FROM EmployeeSkill
WHERE skill IN (SELECT skill FROM RequiredSkill)
GROUP BY emp_id
HAVING
  COUNT(DISTINCT skill) = (
      SELECT COUNT(*) FROM RequiredSkill
    );
IN を EXISTS で置き換える
SELECT emp_id
FROM EmployeeSkill ES
WHERE EXISTS (
    SELECT 1
    FROM RequiredSkill RS
    WHERE RS.skill = ES.skill
  )
GROUP BY emp_id
HAVING
  COUNT(DISTINCT ES.skill) = (
      SELECT COUNT(*) FROM RequiredSkill
    );

メリット

  • 結合キーでインデックスを使える可能性がある
  • 全表検索の必要がない（1 行でも条件を満たす行が存在したらそこで検索を打ち切るため）
IN を INNER JOIN で置き換える
SELECT ES.emp_id
FROM
  EmployeeSkill ES
    INNER JOIN RequiredSkill RS
      ON ES.skill = RS.skill
GROUP BY ES.emp_id
HAVING
  COUNT(DISTINCT ES.skill) = (
      SELECT COUNT(*) FROM RequiredSkill
    );

メリット

  • 結合キーでインデックスを使える可能性がある
  • 中間ビューが作られない（サブクエリがなくなるため）

2.4.3 減法で表現する

SELECT DISTINCT emp_id
FROM EmployeeSkill ES
WHERE NOT EXISTS (
    SELECT skill
    FROM RequiredSkill
    EXCEPT
    SELECT skill
    FROM EmployeeSkill ES2
    WHERE ES2.emp_id = ES.emp_id
  );

3. 結合と集合演算

ex.

各結合について、次のテーブル（再掲）に対するクエリを例示する。

A テーブル
id name
1 太郎
2 花子
3 次郎
B テーブル
id name
1 太郎
2 花子
4 三郎

3.1 交差結合（CROSS JOIN）

直積（再掲）

SELECT
  A.name AS a_name,
  B.name AS b_name
FROM
  A CROSS JOIN B;
結果
a_name b_name
太郎 太郎
太郎 花子
太郎 三郎
花子 太郎
花子 花子
花子 三郎
次郎 太郎
次郎 花子
次郎 三郎

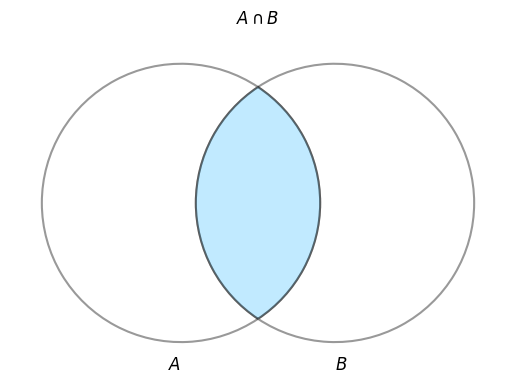
3.2 内部結合（INNER JOIN）

論理積（INTERSECT）

SELECT
  A.name AS a_name,
  B.name AS b_name
FROM
  A INNER JOIN B
    ON A.id = B.id;
結果
a_name b_name
太郎 太郎
花子 花子

3.3.1 完全外部結合（FULL OUTER JOIN）

論理和（UNION）

SELECT
  A.name AS a_name,
  B.name AS b_name
FROM
  A FULL OUTER JOIN B
    ON A.id = B.id;
結果
a_name b_name
太郎 太郎
花子 花子
次郎
三郎

排他的論理和

SELECT
  COALESCE(A.name, B.name) AS name
FROM
  A FULL OUTER JOIN B
    ON A.id = B.id
WHERE
  A.name IS NULL
  OR B.name IS NULL;
結果
name
次郎
三郎

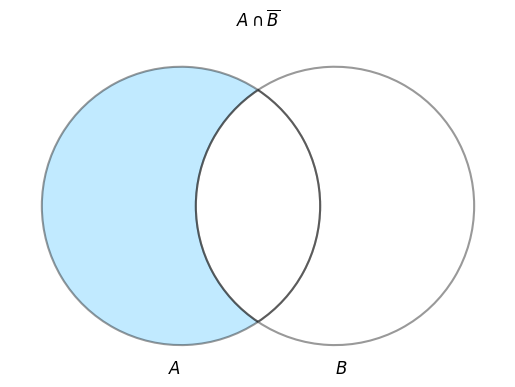
3.3.2 左外部結合（LEFT OUTER JOIN）

A - B 

SELECT
  A.name AS a_name
FROM
  A LEFT OUTER JOIN B
    ON A.id = B.id
WHERE
  B.name IS NULL;
結果
a_name
次郎

3.3.3 右外部結合（RIGHT OUTER JOIN）

B - A 

SELECT
  B.name AS B_name
FROM
  A RIGHT OUTER JOIN B
    ON A.id = B.id
WHERE
  A.name IS NULL;
結果
b_name
三郎

Discussion