📝

Pythonで学ぶデジタル信号処理（2離散時間信号とシステム①）

2023/06/04に公開

Python

信号処理

tech

離散時間信号の表現と性質

離散時間信号は、ディジタル信号処理において非常に重要な役割を果たします。この記事では、離散時間信号の表現と性質について詳しく説明します。

離散時間信号とは

離散時間信号は、時間が離散的な値を取る信号です。つまり、時間が連続的ではなく、一定の時間間隔で値がサンプリングされたものです。離散時間信号は、アナログ信号をディジタル化する際に生成されます。離散時間信号は、離散時間インデックスと信号値のペアの集合として以下のように表現されます。離散時間インデックスはサンプリング周波数で正規化された時間を表します。

..., f[-1], f[0], f[1], ...

離散時間信号の性質

性質①離散時間での周期性

1サンプリング周期あたりに進む位相を正規化各周波数と呼び、 $ω$ で表します。

x[n]=cos{\omega}n

について、 $ω=π/4$ の場合 $とω=2$ の場合について考えると、

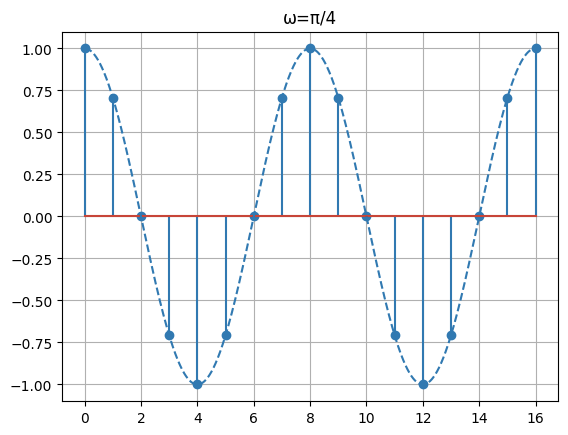
omega_pi/4

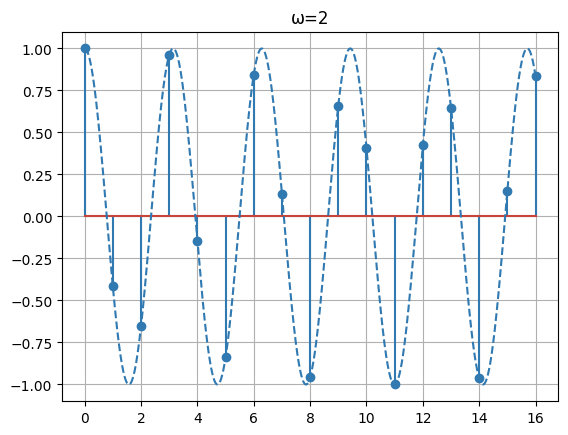
omega_2

本来ならば、周期 $T=2π/ω=2π/2=π$ の周期関数ですが、離散化により周期性がなくなっていることがわかります。

性質②正規化角周波数に2πを足すと、元に戻る

$ω=π/4$ に $2π$ を足すと、

x[n]=cos{\omega}n =cos({\omega+2\pi})n =cos{\omega}n

グラフで表すと、
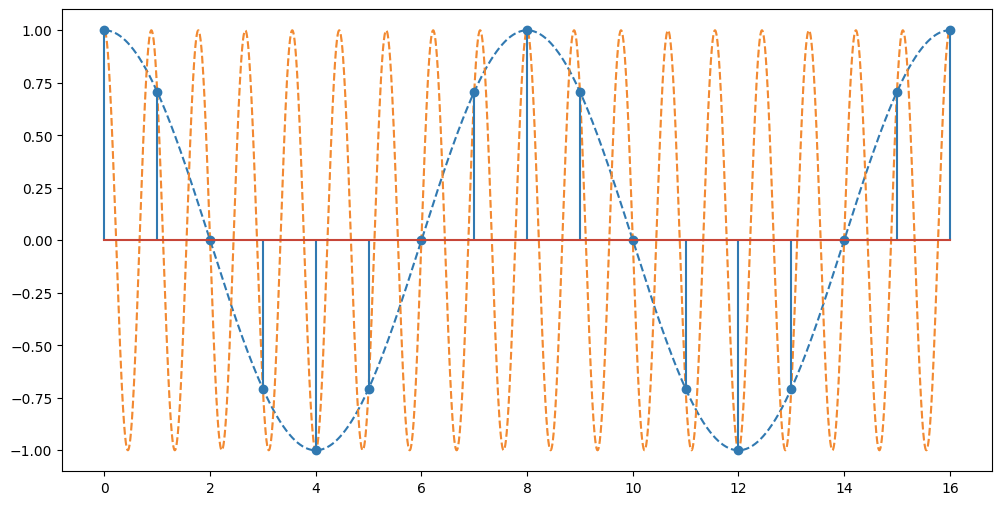
omega_plus_2pi

サンプリング1回の間に1周期増えることで、離散化後は同じ値を取っていることがわかる

使用コード

# ライブラリのインポート

import numpy as np
import matplotlib.pyplot as plt

# 性質①
n = np.arange(0, 17, 1)
omega1 = np.pi / 4
omega2 = 2
x1 = np.cos(omega1 * n)
x2 = np.cos(omega2 * n)

t = np.arange(0, 16.001, 0.001)
y1 = np.cos(omega1 * t)
y2 = np.cos(omega2 * t)

plt.stem(n, x1)
plt.plot(t, y1, linestyle="dashed")
plt.grid()
plt.title("ω=π/4")
plt.show()

plt.stem(n, x2)
plt.plot(t, y2, linestyle="dashed")
plt.grid()
plt.title("ω=2")
plt.show()

# 性質②
omega3 = omega1 + 2*np.pi
y3 = np.cos(omega3*t)
x3 = np.cos(omega3*n)

fig = plt.figure(figsize=(12, 6))
plt.plot(t, y1, ls="--")
plt.plot(t, y3, ls="--")
plt.stem(n, x3)
plt.show()