📊

[解析手法] - 多次元版最小二乗法

2024/02/13に公開

math

はじめに

「最小二乗法」はデータ解析やデータの応用において大変有用です。
しかし、この手法は「x-y平面のグラフに直線を引く」という利用法が多く、他のページで解説されているのもこの直線近似の手法ばかりが目立ちます。
もっと多彩な応用があるのに、直線近似の利用法ばかりが目立つのは大変もったいなく思います。

今回は、この最小二乗法を多次元空間に適用する場合を考えてみます。
つまり、

$(n-1)$ 個の説明変数 ${\bm x}=(x^0, x^1, \cdots, x^{n-1})$ と、その説明変数ベクトル ${\bm x}$ によって決まる値 $z({\bm x})$ が分布する n次元空間において、 $z({\bm x})$ との二乗誤差が最小となるような超平面関数（回帰関数） $f({\bm x})$ を導出する

というような場合です。
３次元空間で直感的に理解するなら、

座標 $(x,y)$ によって表される値 $z(x,y)$ があり、この値 $z$ との二乗誤差を最小にするような起伏を表す平面関数 $f(x,y)$ を導出する

といった感じでしょうか。

3d最小二乗平面イメージ
Fig.1 ３次元空間内のデータ点に対する回帰平面の例

尚、「最小二乗法の意味」として相加平均との関連を以前に記事にしていますので、ご興味のある方はそちらもご一読ください。

導かれる結果

最初に今回の結果だけ示しておこうと思います。
今回の帰結は以下の３つです。

1. 多次元版最小二乗法であっても、帰結は正規方程式 $G^t G \bm{a} = G^t \bm{y}$

多次元版とはいえ最小二乗法なので、結局求めるものは各項の係数です。
どんな多項式の係数なのかはあとに回して、この係数ベクトルを $\bm{a}$ 、従属変数（目的変数）の値ベクトルを $\bm{y}$ とすると、 $\bm{a}$ を求める式は以下となります。

\begin{aligned} & G^{t}G \bm{a} = G^{t} \bm{y} \\ \therefore \quad & \bm{a} = \left( G^{t}G \right)^{-1} G^{t} \bm{y} \end{aligned}

なんてことはない、いつもの正規方程式が帰結になります。

2. $x^d$ - $y$ 平面の関数形を指定する方法を採用する場合の回帰関数

n次元空間全体にわたる超曲面の関数形を考えることを諦め、各 $x^d$ - $y$ 平面の関数の形を指定する方法を採用する場合は、回帰関数を以下の形で与えることができます。

\begin{aligned} f(\bm{x}) = g^1(x^1) g^2(x^2) \cdots g^{n-1}(x^{n-1}) \qquad \left( \bm{x} = (x^1, x^2, \cdots, x^{n-1}) \right) \end{aligned}

ここで右上の添字は次元軸を表すとします。
$g^d(x^d)$ はその $x^d$ - $y$ 平面での関数形を表す任意の既知関数です。

3. 説明変数の座標点が直積集合で表される場合の行列 $G$

説明変数 $\bm{x}_i=(x^1, x^2, \cdots, x^{n-1})_i$ の全体が、各座標軸上の直積集合で表されるとき、

\{ \bm{x}_{i \in N}\} = \{x^1_{i \in N_1}\} \times \{x^2_{i \in N_2}\} \times \cdots \times \{x^{n-1}_{i \in N_{n-1}}\}

正規方程式に出てくる行列 $G$ は以下で与えることができます。

\begin{aligned} G &= \begin{bmatrix} g^1_0(x^1_0) & g^1_1(x^1_0) & \cdots & g^1_{M^1}(x^1_0) \\ g^1_0(x^1_1) & g^1_1(x^1_1) & \cdots & g^1_{M^1}(x^1_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^1_0(x^1_{N_1}) & g^1_1(x^1_{N_1}) & \cdots & g^1_{M^1}(x^1_{N_1}) \end{bmatrix} \otimes \begin{bmatrix} g^2_0(x^2_0) & g^2_1(x^2_0) & \cdots & g^2_{M^2}(x^2_0) \\ g^2_0(x^2_1) & g^2_1(x^2_1) & \cdots & g^2_{M^2}(x^2_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^2_0(x^2_{N_2}) & g^2_1(x^2_{N_2}) & \cdots & g^2_{M^2}(x^2_{N_2}) \end{bmatrix} \otimes \cdots \\ & \cdots \otimes \begin{bmatrix} g^{n-1}_0(x^{n-1}_0) & g^{n-1}_1(x^{n-1}_0) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_0) \\ g^{n-1}_0(x^{n-1}_1) & g^{n-1}_1(x^{n-1}_1) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^{n-1}_0(x^{n-1}_{N_{n-1}}) & g^{n-1}_1(x^{n-1}_{N_{n-1}}) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_{N_{n-1}}) \end{bmatrix} \end{aligned}

$\otimes$ はクロネッカー積（テンソル積）をとる二項演算子です。

1 -> 2 -> 3 と進むにつれて適用範囲が狭くなっていきます（適用可能条件が増えていきます）。
しかし、計算の手間はその分少なくなっていきます。

数学記号ばかり並びますが、帰結は結構簡単です。
最後に R と Python のサンプルコードも載せているので、参考にしてみてください。

それでは以下、これらを順に導出していくことにします。

【1】多変数関数版最小二乗法

多変数関数版の最小二乗法の係数導出がどうなるのかを述べておきます。

最小二乗法の前提

最小二乗法なので、以下の３つの前提が置かれます。

各データ $(x^1, x^2, \cdots, x^{n-1}, y)_i$ は回帰関数 $f(x^1, x^2, \cdots, x^{n-1})$ と正規分布 $N(0, \sigma^2)$ に従う誤差 $\varepsilon$ を用いて以下で表される。

y_i = f(x^1_i, x^2_i, \cdots, x^{n-1}_i) + \varepsilon

回帰関数 $f(x^1, x^2, \cdots, x^{n-1})$ は既知の関数 $g_i(x^1, x^2, \cdots, x^{n-1})$ を用いて、以下の線型結合で表される。

f(\bm{x}) = \sum_{j=0}^{M-1} a_j g_j(\bm{x}) \\ \because \quad \bm{x}=(x^1, x^2, \cdots, x^{n-1})

データ数 $N$ と回帰関数の項数 $M$ の関係は以下である。

M \leq N

この前提をもとに回帰関数 $f(\bm{x})$ の係数を求めていくのが最小二乗法です。

係数導出計算

多次元版であっても行うことはいつもの最小二乗法の計算とまったく同一です。

まず二乗誤差を以下で定義します。

E = \sum_{i=0}^{N-1} (f(\bm{x}_i) - y_i)^2

この $E$ を最小にする係数ベクトル $\bm{a}$ を求めます。
いま「前提２」により、係数ベクトルの要素である各係数の符号は「正」となっています。
したがってこの $E$ は各係数 $a_k$ に関して凸関数となります。
（二次関数的に言えば、下に凸のグラフです）
また、二乗関数であることから「極小値＝最小値」となります。

これより、この $E$ を各係数 $a_k$ で偏微分し 0 とおいた連立方程式の解が求める係数ベクトル $\bm{a}$ となります。

$E$ を各 $a_k$ で微分して整理します。

\begin{aligned} \frac{\partial E}{\partial a_k} &= \frac{\partial}{\partial a_k} \left\{ \sum_{i=0}^{N-1}(f(\bm{x}_i)-y_i)^2 \right\} \\ &= \frac{\partial}{\partial a_k}\left\{\sum_{i=0}^{N-1}\left(\sum_{j=0}^{M-1}a_jg_j(\bm{x}_i)-y_i\right)^2\right\} \\ &= 2\sum_{i=0}^{N-1}\left(\sum_{j=0}^{M-1}a_jg_j(\bm{x}_i)-y_i\right)\frac{\partial}{\partial a_k}\left(\sum_{j=0}^{M-1}a_jg_j(\bm{x}_i)-y_i\right) \\ &= 2\sum_{i=0}^{N-1}\left(\sum_{j=0}^{M-1}a_jg_j(\bm{x}_i)-y_i\right)g_k(\bm{x}_i) \\ &= 2\sum_{i=0}^{N-1}\sum_{j=0}^{M-1}a_jg_j(\bm{x}_i)g_k(\bm{x}_i)-2\sum_{i=0}^{N-1}y_ig_k(\bm{x}_i) \\ &= 0 \\ \\ ∴　&\sum_{i=0}^{N-1}\sum_{j=0}^{M-1}a_jg_j(\bm{x}_i)g_k(\bm{x}_i)=\sum_{i=0}^{N-1}y_ig_k(\bm{x}_i) \end{aligned}

これを行列にして整理すれば、

\scriptsize{ \begin{aligned} \begin{bmatrix} g_0(\bm{x}_0) & g_0(\bm{x}_1) & \cdots & g_0(\bm{x}_{N-1}) \\ g_1(\bm{x}_0) & g_1(\bm{x}_1) & \cdots & g_1(\bm{x}_{N-1}) \\ \vdots & \vdots & \ddots & \vdots \\ g_{M-1}(\bm{x}_0) & g_{M-1}(\bm{x}_1) & \cdots & g_{M-1}(\bm{x}_{N-1}) \\ \end{bmatrix} \begin{bmatrix} g_0(\bm{x}_0) & g_1(\bm{x}_0) & \cdots & g_{M-1}(\bm{x}_0) \\ g_0(\bm{x}_1) & g_1(\bm{x}_1) & \cdots & g_{M-1}(\bm{x}_1) \\ \vdots & \vdots & \ddots & \vdots \\ g_0(\bm{x}_{N-1}) & g_1(\bm{x}_{N-1}) & \cdots & g_{M-1}(\bm{x}_{N-1}) \\ \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{M-1} \end{bmatrix} \\ = \begin{bmatrix} g_0(\bm{x}_0) & g_0(\bm{x}_1) & \cdots & g_0(\bm{x}_{N-1}) \\ g_1(\bm{x}_0) & g_1(\bm{x}_1) & \cdots & g_1(\bm{x}_{N-1}) \\ \vdots & \vdots & \ddots & \vdots \\ g_{M-1}(\bm{x}_0) & g_{M-1}(\bm{x}_1) & \cdots & g_{M-1}(\bm{x}_{N-1}) \\ \end{bmatrix} \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_{N-1} \end{bmatrix} \end{aligned} }

行列とベクトルをそれぞれ $G, \bm{a}, \bm{y}$ で表せば、

G^t G \bm{a} = G^t \bm{y}

いつもの正規方程式となります。
既知関数 $g_j(\bm{x})$ を適切に選べば $G^t G$ は正則行列となるので、係数ベクトルは逆行列を用いて

\bm{a} = (G^t G)^{-1} G^t \bm{y}

と求まります。

これから分かるように、n次元空間上の多変数関数による最小二乗法であっても、既知の多変数関数である

g_j(\bm{x}) = g_j(x^1, x^2, \cdots, x^{n-1}) \qquad j \in \{ 0, 1, \cdots, M-1 \}

を任意に選んで、正規方程式から係数ベクトル $\bm{a}$ を求めればよいことがわかります。

【2】任意多変数関数 $g_j(\bm{x})$ の選択

n次元空間上において多変数関数による最小二乗法を適用する場合においても、任意の多変数関数 $g_j(\bm{x})$ の線型結合を考え、正規方程式によりその多変数関数の係数を求めれば良いことがわかりました。
n次元空間において適用するときには、任意の M[個] の(n-1)変数関数 $g_j(\bm{x})$ を選択して上記計算を実行すれば最小二乗法による回帰超曲面を求めることができます。

多変数関数最小二乗法の話としては、これで以上です。

しかし、実際に実行するときになると悩むことがあります。
それは、

任意の多変数関数 $g_j(\bm{x})$ に何を選んだら良いのか？

です。
例えば、
「３次元空間内に散らばるデータ点を平面で最小二乗近似したいとき、この $g_j(\bm{x})$ に何を選べば平面回帰が可能になるのか?」
など、自分が予想するモデルに合う多変数関数を考える必要があります。

3次元空間内の最小二乗平面回帰

3次元空間内の平面近似
Fig.2 3次元空間内の最小二乗平面近似

実際の例として、Fig.2 に示すデータ点に対し平面で最小二乗近似した平面の方程式は以下になります。

f(x,y) = -44 + 9 x + 4.6 y

この場合、任意の多変数関数は以下です。

g_0(x, y) = 1 \\ g_1(x, y) = x \\ g_2(x, y) = y

この任意多変数関数を導出する方法を簡単に説明すると以下になります。

法線ベクトル $\bm{n}=(a,b,c)$ を持つ平面上にあるベクトル $\bm{u}=(u,v,w)$ は、この法線ベクトル $\bm{n}$ との内積がゼロになります。

\begin{aligned} \bm{n} \cdot \bm{u} &= (a, b, c) \cdot (u, v, w) \\ &= au + bv + cw \\ &= 0 \\\\ \therefore w &= \frac{-a}{c}u + \frac{-b}{c}v \\ \bm{u} &= (u, v, \frac{-a}{c}u + \frac{-b}{c}v) \end{aligned}

この $\bm{u}$ にバイアスベクトル $\bm{b}=(p,q,r)$ を加えたものが平面の位置ベクトルになるので、

\begin{aligned} \bm{x} &= \bm{u} + \bm{b} \\ &= (u+p, v+q, \frac{-a}{c}u + \frac{-b}{c}v + r) \end{aligned}

整理すると、

\begin{aligned} x &= u+p \\ y &= v+q \\ z &= \frac{-a}{c}u + \frac{-b}{c}v + r \\ &= \frac{-a}{c}(x-p) + \frac{-b}{c}(y-q) + r \\ &= \frac{-a}{c}x + \frac{-b}{c}y + (r + \frac{ap}{c} + \frac{bq}{c}) \\ &= Ax + By + C \end{aligned}

$A, B, C$ は係数なので、平面近似をするための任意多変数関数は $1, x, y$ であることがわかります。

関数形がわかっている曲面の利用

上記のように導かなくても、自分が予想している曲面の空間多項方程式があらかじめわかっている場合、そのままそれを利用することができます。
Fig.3 は３次元空間内において放物面で最小二乗法を適用した例です。

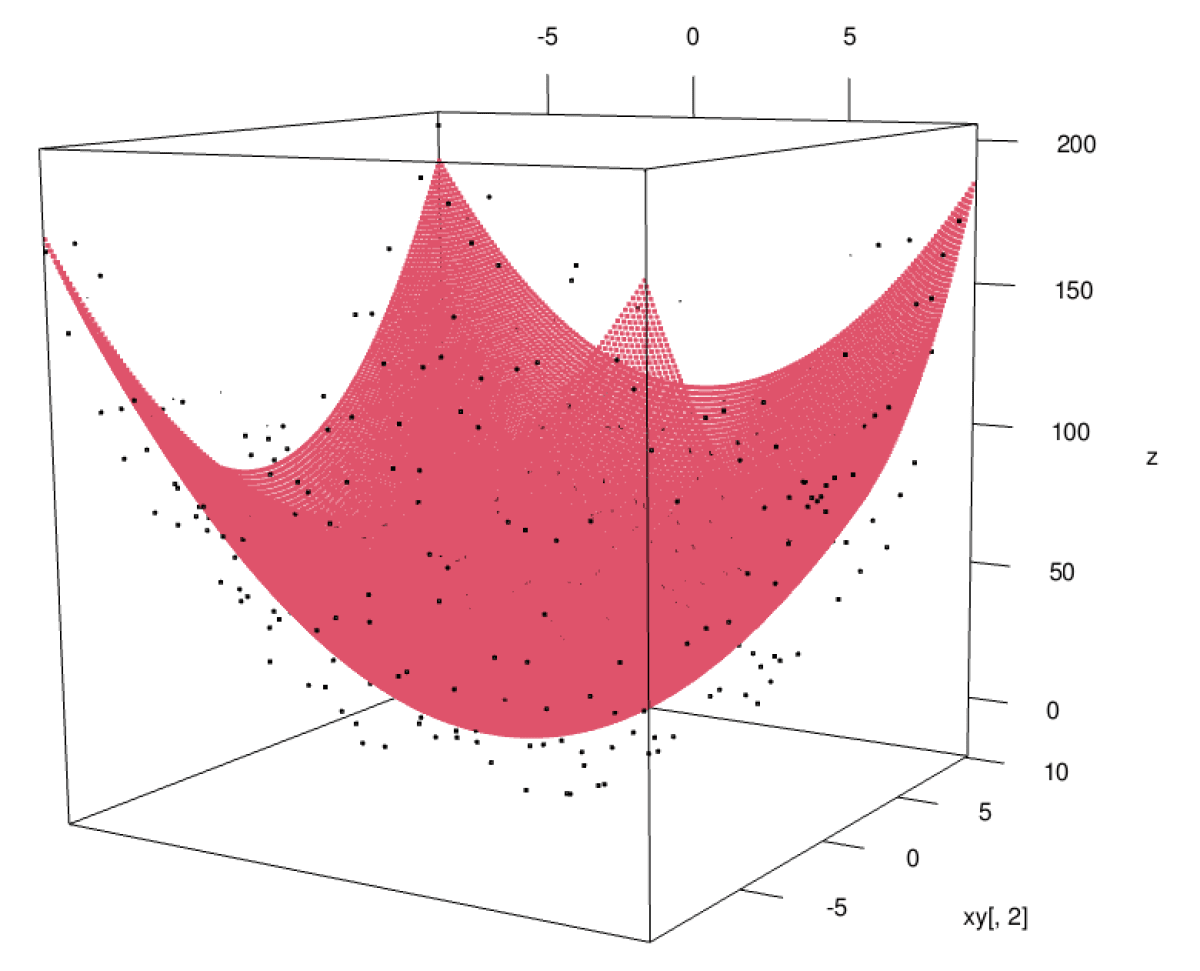
Fig.3 3次元空間内の最小二乗放物面回帰

放物面の方程式は以下なので、

z = A x^2 + B y^2 + C

係数 $A, B, C$ がそれぞれかかっている $x^2, y^2, 1$ が　 $g_i(\bm{x})$ であるとわかります。

このように、自分が予想した曲面にを表す空間多項方程式をあらかじめ把握し、 $g_j(\bm{x})$ に当てはめる必要があります。
しかし、多次元空間内で自分の予想に合う空間多項方程式をあらかじめ把握するのは、なかなか難しいと思います。

座標軸ごとの関数形に着目した $g_j(\bm{x})$ の選択方法

本質的には上記のように、自分が予想する多次元空間多項式を自分で用意するしかありません。

しかし少し条件を緩めて以下のように考えると、任意の多変数関数 $g_j(\bm{x})$ を簡単に用意することができます。

各説明変数軸と目的変数軸とで表される２次元平面グラフの関数形を決める

ある説明変数の座標軸と目的変数の座標軸のグラフを作って、そこの関数の形を指定する、それを全説明変数分行うということです。

また３次元で説明します。
Fig.4 はある3次元空間内のデータに対し最小二乗法で回帰曲面を求めたものです。

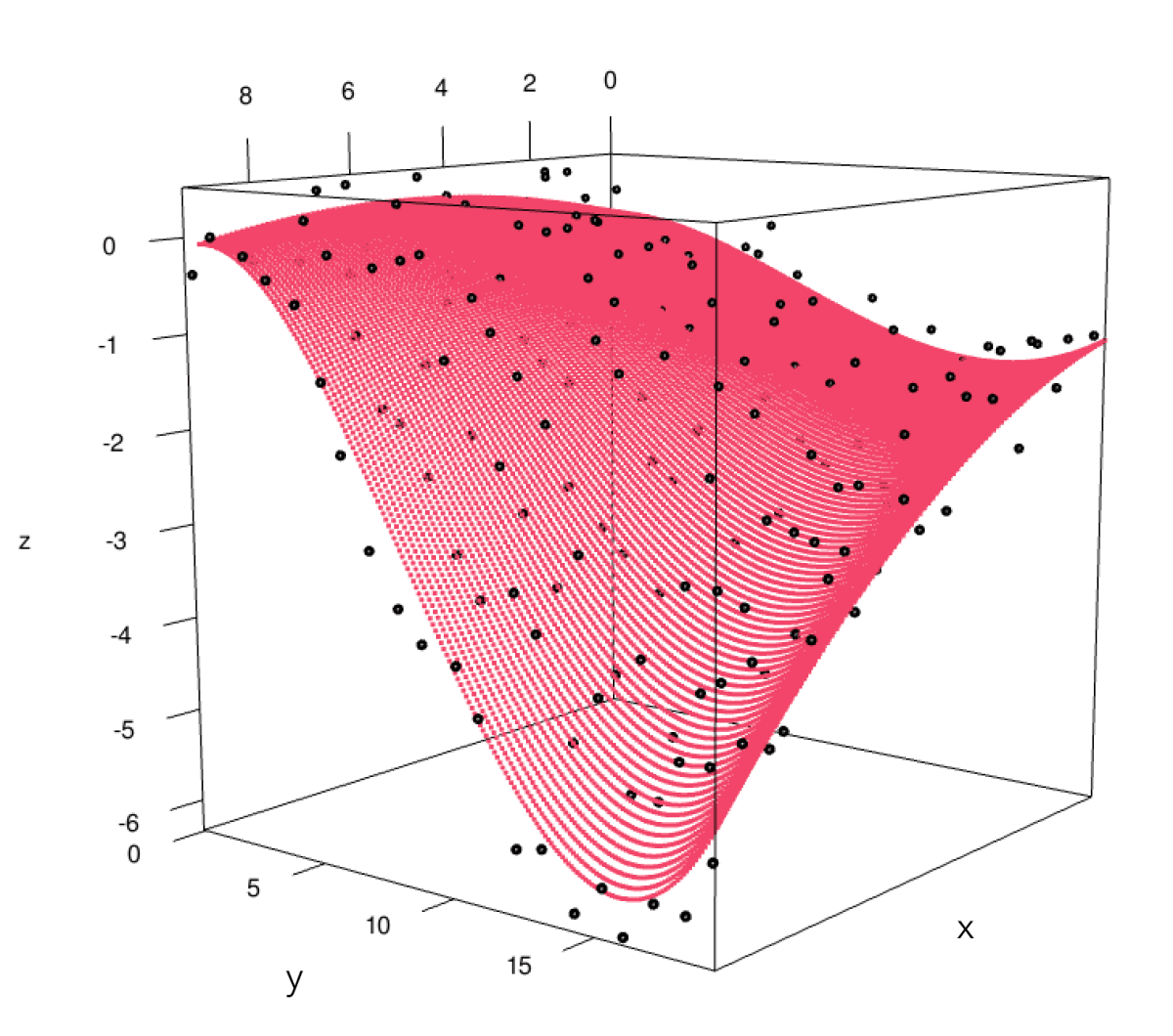
Fig.4 あるデータに対する最小二乗曲面

$x$ - $z$ 平面、 $y$ - $z$ 平面に着目してみてください。
３次元の場合、任意の $y$ 軸の値で切断すれば $x$ - $z$ 平面が、任意の $x$ 軸の値で切断すれば $y$ - $z$ 平面が得られます。

この最小二乗曲面のグラフは、どの $y$ 値の $x$ - $z$ 平面であっても（どの $y$ 値でグラフを切っても）「二次関数」の形をしています。
また、どの $x$ 値の $y$ - $z$ 平面であっても「三次関数」の形をしています。

いまこのグラフでは $x, y$ が説明変数で $z$ が目的変数ですから、

説明変数 $x$ と目的変数 $z$ のグラフは「二次関数」
説明変数 $y$ と目的変数 $z$ のグラフは「三次関数」

と関数形がなるように $g_j(\bm{x})$ を選択してこの回帰曲面求めました。
n次元の場合も、

説明変数 $x^d$ と目的変数 $y$ のグラフは「○○関数」

というように、全ての説明変数と目的変数のペアに対して関数形を決めれば、必要となる多変数関数 $g_j(\bm{x})$ を自動的に用意することができます。

$x^d$ - $y$ 平面の関数形が $g^d(x^d)$ であるような曲面方程式

では、どのようにすれば $x^d$ - $y$ 平面の関数形が任意の関数形になるように変数関数 $g_j(\bm{x})$ を選択できるのか？
答えは単純で、以下のように回帰関数を構成してやれば解決します。

f(\bm{x}) = g^1(x^1) g^2(x^2) \cdots g^{n-1}(x^{n-1})

ここで $g^d(x^d)$ はその $x^d$ 座標軸と目的変数軸との関数形を与える１変数関数です。

実際、任意に $x^d$ を選びそれ以外の説明変数をある値に固定してやると、この式は以下のようになります。

\begin{aligned} f(\bm{x})&|_{x^1=c_1, x^2=c_2, \cdots, x^{d-1}=c_{d-1}, x^{d+1}=c_{d+1}, \cdots, x^{n-1}=c_{n-1}} \\ &= g^1(c_1) g^2(c_2) \cdots g^d(x^d) \cdots g^{n-1}(c_{n-1}) \\ &= (C_1 C_2 \cdots C_{d-1} C_{d+1} \cdots C_{n-1}) \cdot g^d(x^d) \\ &= C \cdot g^d(x^d) \end{aligned}

これは選択した関数 $g^d(x^d)$ の $C$ 倍ですから、意図した通り $x^d$ - $y$ 平面の関数形が $g^d(x^d)$ となっています。
たとえば二次方程式を選択したら二次方程式、三角関数を選択したら三角関数の関数の形となります。

３次元空間での具体例で説明します。
まず回帰曲面として、以下のような条件を選択をしたとします。

$x$ - $z$ 平面での関数の形は２次関数
$y$ - $z$ 平面での関数の形は３次関数

（これは先ほどの例と同じ関数形を選択しています）
このような特徴を持つ曲面の方程式は以下になります。

f(x, y) = (a_0 + a_1 x + a_2 x^2)(b_0 + b_1 y + b_2 y^2 + b_3 y^3)

変数が $x$ の部分は２次関数、変数が $y$ の部分は３次関数で、これらを掛け算で結合している形です。
これであれば、 $x$ がある値に固定されれば $y$ の３次関数、 $y$ がある値に固定されれば $x$ の２次関数になることは容易に理解できます。

\begin{aligned} f(c, y)&=(a_0 + a_1 c + a_2 c^2)(b_0 + b_1 y + b_2 y^2 + b_3 y^3) \\ &= C_x \cdot (b_0 + b_1 y + b_2 y^2 + b_3 y^3) \\ &= C_x b_0 + C_x b_1 y + C_x b_2 y^2 + C_x b_3 y^3 \\ f(x, c)&=(a_0 + a_1 x + a_2 x^2)(b_0 + b_1 c + b_2 c^2 + b_3 c^3) \\ &= (a_0 + a_1 x + a_2 x^2) \cdot C_y \\ &= C_y a_0 + C_y a_1 x + C_y a_2 x^2 \end{aligned}

$x$ がある値 $c$ に固定されるということは $x=c$ である $y$ - $z$ 平面を選択したことになるので、その平面での関数の形は３次関数であることがわかります。
他の場合も同様です。

これは、任意の $x^d$ - $y$ 平面の関数形を $g^d(x^d)$ に定めたことを意味します。

$x^d$ - $y$ 平面の関数形が $g^d(x^d)$ であるような曲面方程式の $g_j(\bm{x})$

ではここから導かれる $g_j(\bm{x})$ はどんな関数でしょうか？

これも簡単で、上で定めた式を展開すれば求まります。
$g^d(x^d)$ は特殊な関数を選ばない限り、0 にならなければ制限は特にないのですが、利用頻度が高いであろう多項式であるとして話を進めます。
すると $g^d(x^d)$ は

g^d(x^d) = \sum_{j} c_j^{d} g_{j}^{d}(x^d)

とで表されるので、上の式に代入し展開すれば、

\begin{aligned} f(\bm{x}) &= g^1(x^1) g^2(x^2) \cdots g^{n-1}(x^{n-1}) \\ &= \left(\sum_{j_1} c_{j_1}^{1} g_{j_1}^{1}(x^1) \right) \left( \sum_{j_2} c_{j_2}^{2} g_{j_2}^{2}(x^2) \right) \cdots \left( \sum_{j_{n-1}} c_{j_{n-1}}^{n-1} g_{j_{n-1}}^{n-1}(x^{n-1}) \right) \\ &= \sum_{j_1} \sum_{j_2} \cdots \sum_{j_{n-1}} c_{j_1}^{1} c_{j_2}^{2} \cdots c_{j_{n-1}}^{n-1} g_{j_{1}}^{1}(x^{1}) g_{j_{2}}^{2}(x^{2}) \cdots g_{j_{n-1}}^{n-1}(x^{n-1}) \end{aligned}

したがって $g_j(\bm{x})$ は

g_j(\bm{x}) = g_{j_{1}}^{1}(x^{1}) g_{j_{2}}^{2}(x^{2}) \cdots g_{j_{n-1}}^{n-1}(x^{n-1})

であることがわかります。

これも先ほどの例に当てはめると、

\begin{aligned} f(x, y) &= (a_0 + a_1 x + a_2 x^2)(b_0 + b_1 y + b_2 y^2 + b_3 y^3) \\ &= a_0 b_0 + a_0 b_1 y + a_0 b_2 y^2 + a_0 b_3 y^3 \\ & \quad + a_1 b_0 x + a_1 b_1 xy + a_1 b_2 xy^2 + a_1 b_3 xy^3 \\ & \quad + a_2 b_0 x^2 + a_2 b_1 x^2y + a_2 b_2 x^2y^2 + a_2 b_3 x^2y^3 \end{aligned}

したがって

\begin{aligned} g_0(x,y) &= 1 \\ g_1(x,y) &= y \\ g_2(x,y) &= y^2 \\ g_3(x,y) &= y^3 \\ g_4(x,y) &= x \\ g_5(x,y) &= xy \\ g_6(x,y) &= xy^2 \\ g_7(x,y) &= xy^3 \\ g_8(x,y) &= x^2 \\ g_9(x,y) &= x^2y \\ g_{10}(x,y) &= x^2y^2 \\ g_{11}(x,y) &= x^2y^3 \end{aligned}

となります。

結局、各 $x^d$ - $y$ 平面の関数形の方程式を掛け算で繋ぎ、全部展開すれば各 $g_i(\bm{x})$ は求められるということになります。
これで $x^d$ - $y$ 平面の関数形を指定する場合の $g_j(\bm{x})$ を求めることができるようになりました。

【3】行列 $G$ の構成法

各 $g_i(\bm{x})$ が求められるようになったので、最小二乗法の正規方程式に出てくる $G$ が構成できるようになりました。
しかし、今回の方法で決めているのは各 $x^d$ - $y$ 平面の関数形 $g^d(x^d)$ 、一方、必要な $g_j(\bm{x})$ は掛け合わせたものを展開しなければ得ることができません。
一般形がわかっているとはいえ、実際に計算を行おうとするとかなり面倒です。
決めた各関数形 $g^d(x^d)$ をそのまま使える、うまい $G$ の構成法はないものでしょうか。

これも以下の条件下であれば良い方法が存在します。

・説明変数の座標点が各説明変数軸での座標点の直積集合で表される場合

\{ \bm{x}_{i \in N}\} = \{x^1_{i \in N_1}\} \times \{x^2_{i \in N_2}\} \times \cdots \times \{x^{n-1}_{i \in N_{n-1}}\}

これは具体的な３変数の場合で示すと、説明変数の座標点が以下のような場合のことになります。

\begin{aligned} \begin{matrix} (x_0, y_0, z_0) & (x_1, y_0, z_0) & \cdots & (x_l, y_0, z_0) \\ (x_0, y_1, z_0) & (x_1, y_1, z_0) & \cdots & (x_l, y_1, z_0) \\ \vdots & \vdots & \ddots & \vdots \\ (x_0, y_m, z_0) & (x_1, y_m, z_0) & \cdots & (x_l, y_m, z_0) \\ \\ (x_0, y_0, z_1) & (x_1, y_0, z_1) & \cdots & (x_l, y_0, z_1) \\ (x_0, y_1, z_1) & (x_1, y_1, z_1) & \cdots & (x_l, y_1, z_1) \\ \vdots & \vdots & \ddots & \vdots \\ (x_0, y_m, z_1) & (x_1, y_m, z_1) & \cdots & (x_l, y_m, z_1) \\ \vdots & \vdots & \ddots & \vdots \\ (x_0, y_0, z_n) & (x_1, y_0, z_n) & \cdots & (x_l, y_0, z_n) \\ (x_0, y_1, z_n) & (x_1, y_1, z_n) & \cdots & (x_l, y_1, z_n) \\ \vdots & \vdots & \ddots & \vdots \\ (x_0, y_m, z_n) & (x_1, y_m, z_n) & \cdots & (x_l, y_m, z_n) \\ \end{matrix} \end{aligned}

全ての座標点が、以下のようにそれぞれの軸での座標点の値の組み合わせで表される場合です。

\{ (x, y, z)_{i}\} = \{x_0, x_1, \cdots, x_l\} \times \{y_0, y_1, \cdots, y_m\} \times \{z_0, z_1, \cdots, z_n\}

これの最も簡単な例は、座標点が格子点である場合 になります。

\begin{aligned} \begin{matrix} (0,0,0) & (1,0,0) & \cdots & (l,0,0) \\ (0,1,0) & (1,1,0) & \cdots & (l,1,0) \\ \vdots & \vdots & \ddots & \vdots \\ (0,m,0) & (1,m,0) & \cdots & (l,m,0) \\ \\ (0,0,1) & (1,0,1) & \cdots & (l, 0, 1) \\ (0, 1, 1) & (1, 1, 1) & \cdots & (l, 1, 1) \\ \vdots & \vdots & \ddots & \vdots \\ (0, m, 1) & (1, m, 1) & \cdots & (l, m, 1) \\ \vdots & \vdots & \ddots & \vdots \\ (0, 0, n) & (1, 0, n) & \cdots & (l, 0, n) \\ (0, 1, n) & (1, 1, n) & \cdots & (l, 1, n) \\ \vdots & \vdots & \ddots & \vdots \\ (0, m, n) & (1, m, n) & \cdots & (l, m, n) \\ \end{matrix} \end{aligned}

3次元空間での $G$ 構成例

これまで用いてきた3次元空間での具体例を使って構成例を考えてみます。

いま $x$ - $z$ 平面、 $y$ - $z$ 平面それぞれの関数形を以下とします。

$x$ - $z$ 平面 : $g^1(x^1)=g^{(x)}(x)=a_0 + a_1 x + a_2 x^2$
$y$ - $z$ 平面 : $g^2(x^2)=g^{(y)}(y)=b_0 + b_1 y + b_2 y^2 + b_3 y^3$

すると、使用する回帰曲面の方程式は以下になります(再掲)。

\begin{aligned} f(x, y) &= g^1(x^1) g^2(x^2) \\ &= g^{(x)}(x) g^{(y)}(y) \\ &= (a_0 + a_1 x + a_2 x^2)(b_0 + b_1 y + b_2 y^2 + b_3 y^3) \\ &= a_0 b_0 + a_0 b_1 y + a_0 b_2 y^2 + a_0 b_3 y^3 \\ & \quad + a_1 b_0 x + a_1 b_1 xy + a_1 b_2 xy^2 + a_1 b_3 xy^3 \\ & \quad + a_2 b_0 x^2 + a_2 b_1 x^2y + a_2 b_2 x^2y^2 + a_2 b_3 x^2y^3 \end{aligned}

ここから $G$ を構成すると以下になります。
尚、ここで説明変数の座標点は $(x, y)_i = (x_i, y_i)$ で、座標点の個数は $N$ [個]とします。

\footnotesize{ \begin{aligned} G &= \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 & x_0 & x_0 y_0 & x_0 {y_0}^2 & x_0 {y_0}^3 & {x_0}^2 & {x_0}^2 y_0 & {x_0}^2 {y_0}^2 & {x_0}^2 {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 & x_1 & x_1 y_1 & x_1 {y_1}^2 & x_1 {y_1}^3 & {x_1}^2 & {x_1}^2 y_1 & {x_1}^2 {y_1}^2 & {x_1}^2 {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & y_N & {y_N}^2 & {y_N}^3 & x_N & x_N y_N & x_N {y_N}^2 & x_N {y_N}^3 & {x_N}^2 & {x_N}^2 y_N & {x_N}^2 {y_N}^2 & {x_N}^2 {y_N}^3 \\ \end{bmatrix} \end{aligned} }

この行列 $G$ は、このままの状態でも２つの行列の積に分解は可能ですが、何も嬉しい効果をもたらしてくれません。
これ以上の変形もできないので、ここで諦めるしかありません。

しかし、先ほどの

説明変数の座標点が各説明変数軸での座標点の直積集合で表される

という条件下であれば、この $G$ をさらに便利な形に変形することができます。
この条件下の場合、説明変数の座標点は $(x_i, y_j)$ というように $x$ と $y$ の添字を別々に書けるので、これを用いて $G$ を書き直すと、

\scriptsize{ \begin{aligned} G &= \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 & x_0 & x_0 y_0 & x_0 {y_0}^2 & x_0 {y_0}^3 & {x_0}^2 & {x_0}^2 y_0 & {x_0}^2 {y_0}^2 & {x_0}^2 {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 & x_0 & x_0 y_1 & x_0 {y_1}^2 & x_0 {y_1}^3 & {x_0}^2 & {x_0}^2 y_1 & {x_0}^2 {y_1}^2 & {x_0}^2 {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 & x_0 & x_0 y_{N_y} & x_0 {y_{N_y}}^2 & x_0 {y_{N_y}}^3 & {x_0}^2 & {x_0}^2 y_{N_y} & {x_0}^2 {y_{N_y}}^2 & {x_0}^2 {y_{N_y}}^3 \\ 1 & y_0 & {y_0}^2 & {y_0}^3 & x_1 & x_1 y_0 & x_1 {y_0}^2 & x_1 {y_0}^3 & {x_1}^2 & {x_1}^2 y_0 & {x_1}^2 {y_0}^2 & {x_1}^2 {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 & x_1 & x_1 y_1 & x_1 {y_1}^2 & x_1 {y_1}^3 & {x_1}^2 & {x_1}^2 y_1 & {x_1}^2 {y_1}^2 & {x_1}^2 {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 & x_1 & x_1 y_{N_y} & x_1 {y_{N_y}}^2 & x_1 {y_{N_y}}^3 & {x_1}^2 & {x_1}^2 y_{N_y} & {x_1}^2 {y_{N_y}}^2 & {x_1}^2 {y_{N_y}}^3 \\ 1 & y_0 & {y_0}^2 & {y_0}^3 & x_2 & x_2 y_0 & x_2 {y_0}^2 & x_2 {y_0}^3 & {x_2}^2 & {x_2}^2 y_0 & {x_2}^2 {y_0}^2 & {x_2}^2 {y_0}^3 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & y_{0} & {y_{0}}^2 & {y_{0}}^3 & x_{N_x} & x_{N_x} y_{0} & x_{N_x} {y_{0}}^2 & x_{N_x} {y_{0}}^3 & {x_{N_x}}^2 & {x_{N_x}}^2 y_{0} & {x_{N_x}}^2 {y_{0}}^2 & {x_{N_x}}^2 {y_{0}}^3 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 & x_{N_x} & x_{N_x} y_{N_y} & x_{N_x} {y_{N_y}}^2 & x_{N_x} {y_{N_y}}^3 & {x_{N_x}}^2 & {x_{N_x}}^2 y_{N_y} & {x_{N_x}}^2 {y_{N_y}}^2 & {x_{N_x}}^2 {y_{N_y}}^3 \\ \end{bmatrix} \end{aligned} }

と書けます。
これをさらに部分行列で書き直すと以下となります。

\scriptsize{ \begin{aligned} G &= \begin{bmatrix} 1 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} & x_0 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} & {x_0}^2 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} \\ 1 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} & x_1 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} & {x_1}^2 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} \\ \vdots & \vdots & \vdots \\ 1 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} & x_{N_x} \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} & {x_{N_x}}^2 \cdot \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} \end{bmatrix} \end{aligned} }

これはちょうど、以下の２つの行列の全ての要素同士を掛け合わせた行列になっていることがわかります。

\begin{aligned} G_1 = \begin{bmatrix} 1 & x_0 & {x_0}^2 \\ 1 & x_1 & {x_1}^2 \\ \vdots & \vdots & \vdots \\ 1 & x_{N_x} & {x_{N_x}}^2 \end{bmatrix} , G_2 = \begin{bmatrix} 1 & y_0 & {y_0}^2 & {y_0}^3 \\ 1 & y_1 & {y_1}^2 & {y_1}^3 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & y_{N_y} & {y_{N_y}}^2 & {y_{N_y}}^3 \end{bmatrix} \end{aligned}

このような、行列 $A$ と $B$ の掛け算で「式の展開」と同じように全ての要素を掛け合わせた結果をもたらす「積算」が存在します。
それは クロネッカー積 です。
クロネッカー積を取る演算記号を $\otimes$ と書くと、上記の $G$ は $G_1$ と $G_2$ を用いて以下のように書けます。

G = G_1 \otimes G_2

$G_1$ は $x$ - $z$ 平面の関数形を決めた２次多項式内に出てくる $x$ の関数に各データ点の $x$ 値を適用して並べたもの
$G_2$ $y$ - $z$ 平面の関数形を決めた３次多項式内に出てくる $y$ の関数に、各データ点の $y$ 値を適用して並べたもの

です。
クロネッカー積を用いることで、掛け算の形で与えられた回帰関数 $f(x,y)$ を展開することなく $G$ を得ることができます。

$n$ 次元空間での $G$ 構成法

3次元での具体的な構成法がわかったので、 $n$ 次元の一般の場合に書き直します。

いま、各 $x^d$ - $y$ 平面の関数形を定め、回帰関数が以下のように表されているとします。

\begin{aligned} f(\bm{x}) &= g^1(x^1) g^2(x^2) \cdots g^{n-1}(x^{n-1})　\\ &= \prod_{d=1}^{n-1} g^d(x^d) \end{aligned}

さらに各 $g^d(x^d)$ は以下のように多項式で表されるとします。

g^d(x^d) = \sum_{j} c_j^{d} g_{j}^{d}(x^d)

これを回帰関数に代入すれば、

\begin{aligned} f(\bm{x}) &= g^1(x^1) g^2(x^2) \cdots g^{n-1}(x^{n-1}) \\ &= \left(\sum_{j_1} c_{j_1}^{1} g_{j_1}^{1}(x^1) \right) \left( \sum_{j_2} c_{j_2}^{2} g_{j_2}^{2}(x^2) \right) \cdots \left( \sum_{j_{n-1}} c_{j_{n-1}}^{n-1} g_{j_{n-1}}^{n-1}(x^{n-1}) \right) \\ &= \sum_{j_1} \sum_{j_2} \cdots \sum_{j_{n-1}} c_{j_1}^{1} c_{j_2}^{2} \cdots c_{j_{n-1}}^{n-1} g_{j_{1}}^{1}(x^{1}) g_{j_{2}}^{2}(x^{2}) \cdots g_{j_{n-1}}^{n-1}(x^{n-1}) \end{aligned}

よって、正規方程式 $G$ は各項の

g_j(\bm{x}) = g_{j_{1}}^{1}(x^{1}) g_{j_{2}}^{2}(x^{2}) \cdots g_{j_{n-1}}^{n-1}(x^{n-1})

を利用して構成されます。

\begin{aligned} G= \begin{bmatrix} g_0(\bm{x}_0) & g_1(\bm{x}_0) & \cdots & g_{M}(\bm{x}_0) \\ g_0(\bm{x}_1) & g_1(\bm{x}_1) & \cdots & g_{M}(\bm{x}_1) \\ \vdots & \vdots & \ddots & \vdots \\ g_0(\bm{x}_{N}) & g_1(\bm{x}_{N}) & \cdots & g_{M}(\bm{x}_{N}) \\ \end{bmatrix} \end{aligned}

さらに、説明変数の座標点 $\{\bm{x}\}$ が各説明変数の座標値 $\{x^d\}$ の直積

\{ \bm{x}_{i \in N}\} = \{x^1_{i \in N_1}\} \times \{x^2_{i \in N_2}\} \times \cdots \times \{x^{n-1}_{i \in N_{n-1}}\}

で表される場合、 $G$ はクロネッカー積を用いて以下で表すことができます。。

\begin{aligned} G &= \begin{bmatrix} g^1_0(x^1_0) & g^1_1(x^1_0) & \cdots & g^1_{M^1}(x^1_0) \\ g^1_0(x^1_1) & g^1_1(x^1_1) & \cdots & g^1_{M^1}(x^1_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^1_0(x^1_{N_1}) & g^1_1(x^1_{N_1}) & \cdots & g^1_{M^1}(x^1_{N_1}) \end{bmatrix} \otimes \begin{bmatrix} g^2_0(x^2_0) & g^2_1(x^2_0) & \cdots & g^2_{M^2}(x^2_0) \\ g^2_0(x^2_1) & g^2_1(x^2_1) & \cdots & g^2_{M^2}(x^2_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^2_0(x^2_{N_2}) & g^2_1(x^2_{N_2}) & \cdots & g^2_{M^2}(x^2_{N_2}) \end{bmatrix} \otimes \cdots \\ & \cdots \otimes \begin{bmatrix} g^{n-1}_0(x^{n-1}_0) & g^{n-1}_1(x^{n-1}_0) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_0) \\ g^{n-1}_0(x^{n-1}_1) & g^{n-1}_1(x^{n-1}_1) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^{n-1}_0(x^{n-1}_{N_{n-1}}) & g^{n-1}_1(x^{n-1}_{N_{n-1}}) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_{N_{n-1}}) \end{bmatrix} \end{aligned}

以上より、正規方程式を構成することが出来、回帰関数の係数を求めることができます。

\begin{aligned} G^t G \bm{a} &= G^t \bm{y} \end{aligned}

３次元空間でのサンプルコード

いろいろ記号を多く書いてきましたがが、言っていることはそんなに難しくはありません。

しかし、「数学記号の式よりコードの方がわかりやすい！」という方もいるかと思います。
そこで上記で３次元の具体例として出していた回帰曲面

f(x, y) = (a_0 + a_1 x + a_2 x^2)(b_0 + b_1 y + b_2 y^2 + b_3 y^3)

を例にしたサンプルコードを置いておきます。
R と Python のコードです。
どちらも同じ内容のコードとなります。

プログラムコードの書き方の良し悪しに関してはご容赦ください。

簡単なコードの解説

先にコードの中身を解説しておこうと思います。

正解曲面関数

データを生成するにあたり、正解となるモデル曲面関数を定義しています。
この曲面関数の値にノイズを加えたものを、推定元のデータとしています。
いろいろ変更してみてください。

データ用意

$x$ , $y$ の説明変数の値と、正解曲面関数から作成される目的変数 $z$ を生成しています。
$x$ , $y$ にもノイズを加えていますが、 $(x,y)$ データ点となったときの座標はちゃんと直積集合で表されるようにしています。

関数形の設定

$x$ - $z$ 平面、 $y$ - $z$ 平面それぞれの関数形をここで決めています。
$g^d_0(x^d), g^d_1(x^d), \cdots$ を並べてベクトル型で返しています。
行列 $G_d$ を作る時に使用します。

ここに並べる関数 $g^d_i(x^d)$ をいろいろ変えて、回帰結果がどうなるか確かめてみてください。

最小二乗法係数計算

クロネッカー積を用いた方法で正規方程式を解いています。
係数ベクトル $\bm{a}$ が求めた最小二乗法の結果です。

推定曲面計算

最小二乗法で求めた係数ベクトルの値を用いて、推定（回帰）された曲面の値を計算しています。
元の $x, y$ の値より細かい座標点となるようにしています。

表示用データ用意

この後のグラフ化をするために必要なデータを作成しています。

検算

推定した結果が正しいか検算をしています。
正規方程式を変形すると、

\begin{aligned} G^t G \bm{a} &= G^t \bm{y} \\ G^t G \bm{a} - G^t \bm{y} &= \bm{o} \\ G^t (G \bm{a} - \bm{y}) &= \bm{o} \end{aligned}

となり、 $G \bm{a} - \bm{y}$ はゼロ因子でなければなりません。
さらに回帰関数に定数項を用いている場合、このベクトルは全ての要素を足し合わせると 0 にならなければならないことがわかります。
くわしくは

をご一読ください。

ここでは推定結果があっているかどうか、 $G \bm{a} - \bm{y}$ の要素を足し合わせてゼロになるかどうかで確かめています。
（実際には丸め誤差などの影響で完全なゼロにならないので、他の値と比べて十分に小さいことを確認してください）

表示

結果を三次元空間にプロットしています。

R のサンプルコード

library(rgl)

#正解曲面関数
Correct_func <- function(xy){
  f1 <- 0.3 + 0.013 * xy[,1] + 0.008 * (xy[,1])^2
  f2 <- 0.03 + 0.005 * (xy[,2]) - 0.07 * (xy[,2])^2 + 0.003 * (xy[,2])^3
  
  return(f1 * f2)
}

#データ用意
x <- seq(0, 9, by=1) + runif(10, -0.2, 0.2)
y <- seq(0, 19, by=1) + runif(10, -0.2, 0.2)

xy <- cbind(
  rep(x, each=length(y)),
  rep(y, length(x))
)

z <- Correct_func(xy) + runif(length(xy[,1]), -0.5, 0.5)

#関数形の設定
## x軸の関数
g1 <- function(x){
  return(c(x^0, x^1, x^2))
}

## y軸の関数
g2 <- function(y){
  return(c(y^0, y^1, y^2, y^3))
}

#最小二乗法係数計算
G1 <- t(sapply(x, g1))
G2 <- t(sapply(y, g2))

G <- G1 %x% G2
GG <- t(G) %*% G

a <- solve(GG, tol = 10^(-100)) %*% t(G) %*% z

#-------------------

#推定曲面計算
u <- seq(0,  9, by=0.1)
v <- seq(0, 19, by=0.1)

uv <- cbind(
  rep(u, each=length(v)),
  rep(v, length(u))
)

H1 <- t(sapply(u, g1))
H2 <- t(sapply(v, g2))
H <- H1 %x% H2


f <- H %*% a

#---------------------

#表示用データ用意
xyz <- cbind(xy, z)
uvw <- cbind(uv, f)

#検算
vrf <- G %*% a
sum(vrf - z)

#表示
plot3d(xyz, xlim=c(min(x), max(x)), ylim=c(min(y), max(y)))
spheres3d(xyz, radius = 0.1)
points3d(uvw, col=2)

Python のサンプルコード

import numpy as np
import random
import matplotlib.pyplot as plt

# 正解曲面関数
def Correct_func(xy):
    f1 = 0.3 + 0.013 * xy[0] + 0.008 * (xy[0])**2
    f2 = 0.03 + 0.005 * (xy[1]) - 0.07 * (xy[1])**2 + 0.003 * (xy[1])**3

    return f1 * f2

# データ用意
x = np.round( np.arange(0, 9.1, 1), 1) + [random.uniform(-0.2, 0.2) for i in range(0, 10)]
y = np.round( np.arange(0, 19.1, 1), 1) + [random.uniform(-0.2, 0.2) for i in range(0, 20)]

xx = np.repeat(x, len(y))
yy = np.tile(y, len(x))

xy = np.stack((xx, yy), axis=1)
del(xx, yy)

z = np.empty(0)
for i in range(0, len(xy[:,0])):
    z = np.append(z, Correct_func(xy[i,:]) + random.uniform(-0.5, 0.5))
del(i)

# 関数形の設定
# x軸の関数
def g1(x):
    return np.array([x**0, x**1, x**2])

# y軸の関数
def g2(y):
    return np.array([y**0, y**1, y**2, y**3])

#最小二乗法係数計算
G1 = g1(x[0])
for i in range(1, len(x)):
    G1 = np.vstack((G1, g1(x[i])))
del(i)

G2 = g2(y[0])
for i in range(1, len(y)):
    G2 = np.vstack((G2, g2(y[i])))
del(i)

G = np.kron(G1, G2)
GG = G.T @ G

a = np.linalg.inv(GG) @ G.T @ z

#------------------
#推定曲面計算
u = np.round( np.arange(0, 9.1, 0.1), 1)
v = np.round( np.arange(0, 19.1, 0.1), 1)

uu = np.repeat(u, len(v))
vv = np.tile(v, len(u))

uv = np.stack((uu, vv), axis=1)
del(uu, vv)

H1 = g1(u[0])
for i in range(1, len(u)):
    H1 = np.vstack((H1, g1(u[i])))
del(i)

H2 = g2(v[0])
for i in range(1, len(v)):
    H2 = np.vstack((H2, g2(v[i])))
del(i)

H = np.kron(H1, H2)

f = H @ a

#------------------
#表示用データ用意
xyz = np.hstack((xy, z.reshape(len(z), 1)))

U = uv[:,0].reshape([len(u), len(v)])
V = uv[:,1].reshape([len(u), len(v)])
W = f.reshape([len(u), len(v)])

#検算
vrf = G @ a
print(sum(vrf - z))

#表示
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(xyz[:,0], xyz[:,1], xyz[:,2], marker=".")
ax.plot_wireframe(U, V, W, color='blue',linewidth=0.3)
plt.show()

まとめ

最後、内容を再度簡単にまとめておきます。

多次元版最小二乗法

既知の多変数関数 $g_i(\bm{x})$ の線形結合として回帰関数を定め、その係数を正規方程式により求める。

f(\bm{x}) = \sum_{j=0}^{M} a_j g_j(\bm{x})

\begin{aligned} G= \begin{bmatrix} g_0(\bm{x}_0) & g_1(\bm{x}_0) & \cdots & g_{M}(\bm{x}_0) \\ g_0(\bm{x}_1) & g_1(\bm{x}_1) & \cdots & g_{M}(\bm{x}_1) \\ \vdots & \vdots & \ddots & \vdots \\ g_0(\bm{x}_{N}) & g_1(\bm{x}_{N}) & \cdots & g_{M}(\bm{x}_{N}) \\ \end{bmatrix} \end{aligned}

G^t G \bm{a} = G^t \bm{y}

$x^d$ - $y$ 平面の関数形を定めて回帰関数を指定する場合

回帰関数は、 $x^d$ - $y$ 平面の関数形 $g^d(x^d)$ を使って以下で表される。

\begin{aligned} f(\bm{x}) = g^1(x^1) g^2(x^2) \cdots g^{n-1}(x^{n-1}) \qquad \left( \bm{x} = (x^1, x^2, \cdots, x^{n-1}) \right) \end{aligned}

説明変数の座標点が各説明変数値の直積で表される場合

上記に加えて、説明変数の座標点が以下のように各説明変数の直積で表される場合、

\{ \bm{x}_{i \in N}\} = \{x^1_{i \in N_1}\} \times \{x^2_{i \in N_2}\} \times \cdots \times \{x^{n-1}_{i \in N_{n-1}}\}

正規方程式に出てくる $G$ は以下のようにクロネッカー積を用いて表すことができる。

\begin{aligned} G &= \begin{bmatrix} g^1_0(x^1_0) & g^1_1(x^1_0) & \cdots & g^1_{M^1}(x^1_0) \\ g^1_0(x^1_1) & g^1_1(x^1_1) & \cdots & g^1_{M^1}(x^1_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^1_0(x^1_{N_1}) & g^1_1(x^1_{N_1}) & \cdots & g^1_{M^1}(x^1_{N_1}) \end{bmatrix} \otimes \begin{bmatrix} g^2_0(x^2_0) & g^2_1(x^2_0) & \cdots & g^2_{M^2}(x^2_0) \\ g^2_0(x^2_1) & g^2_1(x^2_1) & \cdots & g^2_{M^2}(x^2_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^2_0(x^2_{N_2}) & g^2_1(x^2_{N_2}) & \cdots & g^2_{M^2}(x^2_{N_2}) \end{bmatrix} \otimes \cdots \\ & \cdots \otimes \begin{bmatrix} g^{n-1}_0(x^{n-1}_0) & g^{n-1}_1(x^{n-1}_0) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_0) \\ g^{n-1}_0(x^{n-1}_1) & g^{n-1}_1(x^{n-1}_1) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_1) \\ \vdots & \vdots & \ddots & \vdots \\ g^{n-1}_0(x^{n-1}_{N_{n-1}}) & g^{n-1}_1(x^{n-1}_{N_{n-1}}) & \cdots & g^{n-1}_{M^{n-1}}(x^{n-1}_{N_{n-1}}) \end{bmatrix} \end{aligned}

今回の内容は以上です。

最後に

多次元版の最小二乗法について書いてみました。
画像データのRGB値にそれぞれある目的でスムージングをかけたいと思った時がありまして、空間の情報を利用するフィルターが必要にになりました。
単純に最小二乗法を利用すればよいと思ったのですが、３次元以上の場合の最小二乗法が書かれたページがほぼなく、あっても「平面」回帰の情報ばかりだったので、自分で考えてプログラムした時のメモを記事にしてみました。
どなたかの役に立てば幸いです。

間違い、ご感想などありましたらコメント頂けると幸いです。

お読みくださりありがとうございました。