0. そうだ、言語を作ろう

JavaScriptにトランスパイルできて、安全な操作と危険な操作が分離されてて、型が不整合を起こさないような言語を作りたいなあと思った。
ので、作る。

で、型システムを構築してたら色々考えることが多くて試行錯誤して多少まとまってきた部分があるので残しておこうと思う。

1. ジェネリクスのない型システム

最終的にジェネリクスは組み込むつもりだけど、とりあえずそこはおいといてジェネリクスのない型について考える。
JavaScriptへのトランスパイルを考えているので、TypeScriptと同じように number とか string とかそういうやつを扱うことにする。なお any は入れない。もちろん 1 とか 'a' などのリテラル型も扱う。

ジェネリクスを考えない場合、型は集合と同じようなものとして扱うことができる。そのため、以下は集合論の記号を使って型を表現する。

1-1. スーパータイプとサブタイプ

型 A と型 B について、すべての型 A を満たす値が型 B も満たすとき、 A は B のサブタイプである。このことを A \subseteq B と表記する。
また、この時 B は A のスーパータイプであり、 B \supseteq A とも表記できる。つまり、 A \subseteq B \iff B \supseteq A である。

A \subseteq B \land A \supseteq B が成り立つとき、 A = B である。
TypeScriptの世界だとこれが成り立たないケースがあるのだが、少なくとも私の作る言語に関してはこれが成り立つように注意して実装する。

A \subseteq B \land A \ne B であるとき、 A は B の真サブタイプであると言い^[1]、A \subset B と表記する。
同様に、 A \supseteq B \land A \ne B であるとき、 A は B の真スーパータイプであると言い、 A \supset B と表記する。

脚注

1. 真部分集合のようなノリでこう言っているが一般的にそう言うのかどうかは知らない。この文章のなかではそういうことにする。 ↩︎

1-2. 共用型と交差型

A を満たすまたは B を満たす値全体の型を A と B の共用型と言い、 A \cup B と表記する^[1]。
A を満たしかつBを満たす値全体の型を A と B の交差型と言い、 A \cap B と表記する^[2]。

全ての A を満たす値は A \cup B を満たすので、サブタイプの定義から A \subseteq A \cup B である。
また、 A \cap B を満たす値は A を満たすので、同様に A \cap B \subseteq A である。
A を B に置き換えても同様なので、

A \cap B \subseteq A \subseteq A \cup B \\ A \cap B \subseteq B \subseteq A \cup B

が常に成り立つ。

また、 A \ne B のとき、

A \cap B \subset A \subset A \cup B \\ A \cap B \subset B \subset A \cup B

である。

以下が成り立つ（交換法則・結合法則・分配法則）。

A \cup B = B \cup A \\ A \cap B = B \cap A \\ (A \cup B) \cup C = A \cup (B \cup C) \\ (A \cap B) \cap C = A \cap (B \cap C) \\ (A \cup B) \cap C = (A \cap C) \cup (B \cap C) \\ (A \cap B) \cup C = (A \cup C) \cap (B \cup C)

脚注

1. TypeScriptでは A | B と表記される。 ↩︎

2. TypeScriptでは A & B と表記される。 ↩︎

1-3. トップ型とボトム型

\forall X: T \supseteq X となる型 T について考える。
これは存在しうる全ての型 T_1, T_2, .T_3, ... についての共用型 T_1 \cup T_2 \cup T_3 \cup ... のようなものと考えることができる。
このような型をトップ型と言い、 \top と表記する^[1]。

同様に、 \forall X: U \subseteq X となる型 U について考える。
これは存在しうる全ての型 U_1, U_2, .U_3, ... についての交差型 U_1 \cap U_2 \cap U_3 \cap ... のようなものと考えることができる。
このような型をボトム型と言い、 \bot と表記する^[2]。

任意の値はトップ型の値である。
一方、ボトム型の値は全ての型の制約を満たすことになるが、そのような値は存在しない（number でありかつ string である型は存在しないことを考えれば分かるだろう）。そのため、ボトム型は値を持たない型である。

以下が成り立つ。

\top \cup A = \top \\ \top \cap A = A \\ \bot \cup A = A \\ \bot \cap A = \bot

脚注

1. TypeScriptでは unknown がこれに該当する。 ↩︎

2. TypeScriptでは never がこれに該当する。 ↩︎

1-4. 否定型、差分型

任意の型 A について、 A を満たさない値全体を表す型を \lnot A と表記する。
(A \cup B) \cap C のような複合型に対しても、 \lnot \{(A \cup B) \cap C\} と表記する。
なお、型を一文字で表記する時に限り、 \bar A という表記も導入する。 \bar A = \lnot A である。

A から A \cap B の部分を除いた型を差分型と言い、 A \setminus B と表記する。 このとき、 A \setminus B = A \cap \bar B である。

以下が成り立つ。

A \setminus A = A \cap \bar A = \bot \\ \bar A = \top \setminus A \\ A \cup \bar A = \top \\ \bar \bot = \top \\ \bar \top = \bot

また、ド・モルガンの法則が成立する。

\lnot (A \cup B) = \bar A \cap \bar B \\ \lnot (A \cap B) = \bar A \cup \bar B

1-5. 型の広さ

1 のような型と number のような型では、表すことができる範囲が異なる。
1 型の値は 1 しか存在しないが、 1, 2, 42, 3.14, ... など多くの値が number 型になる。
このとき、 1 型より number 型の方が広いと言うことができる。

以下が成立する。

A \supset B のとき、 A は B より広い。

と、これだけであれば、スーパータイプとサブタイプの関係性で済む話なので、わざわざ新たに広さという概念を持ち出したのは意味がある。
スーパータイプとサブタイプの関係性が成り立つのは一部の限定された型だけである。そのため、例えば string と number の広さを比較することはできない。

JavaScriptの number は64bit浮動小数点数のため、表現できる値の種類は NaN を厳密に区別しても 2^64 で、文字列より確実に少ないではないか、と思うかもしれないが、仮にリソースに制限がなかったとしたら有理数と文字列は1対1に対応させることが可能なのでどちらも可算無限という話になり、まあここらへんを突き詰めていくと極限順序数がどうの無限の濃度がどうのという話になるのだがここではそちらに踏み込む必要はないので置いておく。

ここでは、厳密な広さではなく広さレベルとでも言うべきものを導入して考える。number と string はどちらも広さレベル1をとし、\bot は広さレベル0とする。
型 A の広さレベルを \mathrm{ext}(A) と表現しよう。

有限個の広さレベル0または1の型の共用型

\bigcup_{i=1}^n{T_i} = T_1 \cup T_2 \cup ... \cup T_n

を考える。
トップ型は存在しうる全ての型の共用型と捉えることが可能だが、有限個の広さレベル0または1の型で共用体を作ってもトップ型を表現することはできない。

\bigcup_{i=1}^n{T_i} \ne \top (ただし \mathrm{ext}(T_i) = 0, 1)

一方、 \mathrm{ext}(A) = 1 のとき、 A \cup \bar A = \top であるので、 \bar A は広さレベル1ではない。この時の\bar Aの広さレベルを2とする。また、 \top の広さレベルは3とする。

以下が成立する。

\mathrm{ext}(A) = 1 \iff \mathrm{ext}(\bar A) = 2 \\ A = \bot \iff \mathrm{ext}(A) = 0 \\ A = \top \iff \mathrm{ext}(A) = 3

1-6. 型同士の二項関係

既にスーパータイプとサブタイプの関係性に触れたが、それ以外を含めた型同士の関係を定式化できるように拡張したい。

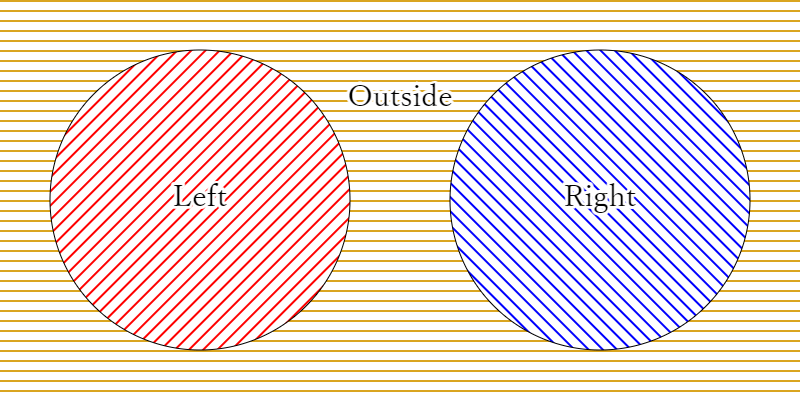
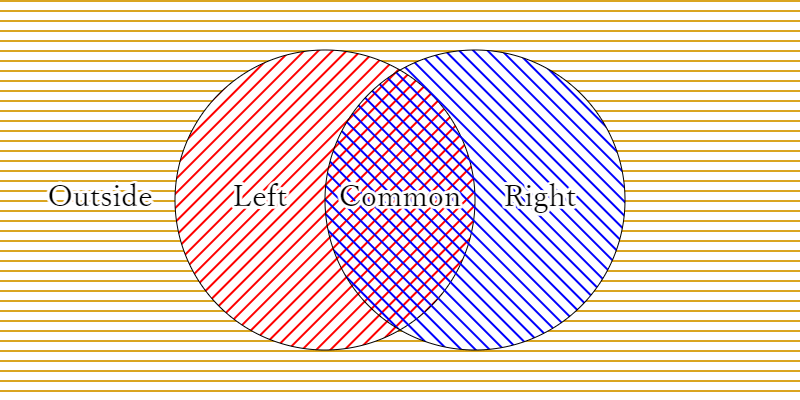
一般に、型 A と型 B があるとき、

A \cap \bar B \\ \bar A \cap B \\ A \cap B \\ \bar A \cap \bar B

の4つの型に分けて考えることができる。

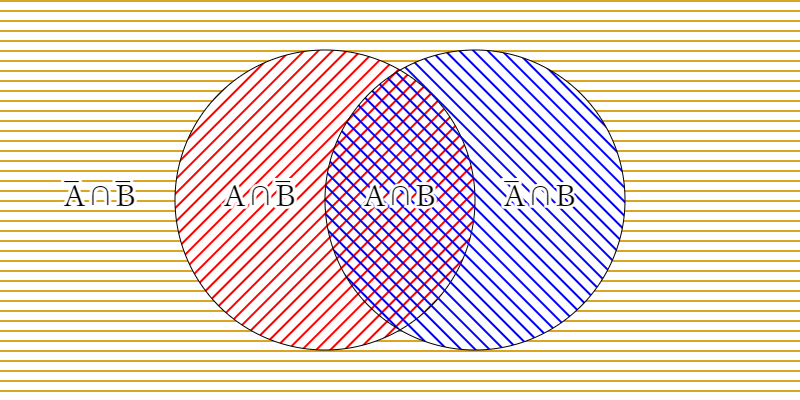
上図においては全ての型が存在するように描いているが、実際は各型は \bot となる可能性がある。
ただし、各型の共用型が \top となるため、全ての型が \bot となることはない。また、いずれか1つの型は広さレベルが2以上となる。

以下、

\begin{aligned} Left = A \cap \bar B \\ Right = \bar A \cap B \\ Common = A \cap B \\ Outside = \bar A \cap \bar B \end{aligned}

とする。また、

\mathrm{exist}(A) = \left\{ \begin{array}{ll} \mathrm{false} & (A = \bot) \\ \mathrm{true} & (A \ne \bot) \end{array} \right.

とすると、 (\mathrm{exist}(Left), \mathrm{exist}(Right), \mathrm{exist}(Common), \mathrm{exist}(Outside)) の状態によって、15通りが考えられる^[1]。

以下、

\begin{aligned} \mathrm{rel}(A, B) &= (\mathrm{exist}(Left), \mathrm{exist}(Right), \mathrm{exist}(Common), \mathrm{exist}(Outside)) \\ &=(l, r, c, o) \end{aligned}

とする。

以下、15通りを列挙するが長くなるので折りたたむ。

1. \mathrm{rel}(A, B) = (\mathrm{false}, \mathrm{false}, \mathrm{false}, \mathrm{true}) の場合。 A = \bot \land B = \bot である。
   
2. \mathrm{rel}(A, B) = (\mathrm{false}, \mathrm{false}, \mathrm{true}, \mathrm{false}) の場合。 A = \top \land B = \top である。
   
3. \mathrm{rel}(A, B) = (\mathrm{false}, \mathrm{false}, \mathrm{true}, \mathrm{true}) の場合。 A = B である。
   
4. \mathrm{rel}(A, B) = (\mathrm{false}, \mathrm{true}, \mathrm{false}, \mathrm{false}) の場合。 A = \bot \land B = \top である。
   
5. \mathrm{rel}(A, B) = (\mathrm{false}, \mathrm{true}, \mathrm{false}, \mathrm{true}) の場合。 A = \bot である。
   
6. \mathrm{rel}(A, B) = (\mathrm{false}, \mathrm{true}, \mathrm{true}, \mathrm{false}) の場合。 B = \top である。
   
7. \mathrm{rel}(A, B) = (\mathrm{false}, \mathrm{true}, \mathrm{true}, \mathrm{true}) の場合。 A \sub B である。
   
8. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{false}, \mathrm{false}, \mathrm{false}) の場合。 A = \top \land B = \bot である。
   
9. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{false}, \mathrm{false}, \mathrm{true}) の場合。 B = \bot である。
   
10. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{false}, \mathrm{true}, \mathrm{false}) の場合。 A = \top である。
    
11. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{false}, \mathrm{true}, \mathrm{true}) の場合。 A \supset B である。
    
12. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{true}, \mathrm{false}, \mathrm{false}) の場合。A = \bar B である。
    
13. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{true}, \mathrm{false}, \mathrm{true}) の場合。 A \cap B = \bot である。
    
14. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{true}, \mathrm{true}, \mathrm{false}) の場合。 A \cup B = \top である。
    
15. \mathrm{rel}(A, B) = (\mathrm{true}, \mathrm{true}, \mathrm{true}, \mathrm{true}) の場合。
    

脚注

1. （ (\mathrm{false}, \mathrm{false}, \mathrm{false}, \mathrm{false}) にはなりえないため 2^4 = 16 より1通り少ない） ↩︎

1-7. 否定型の二項関係

明らかに、

\mathrm{rel}(B, A) = (r, l, c, o)

である。また、

\begin{aligned} \mathrm{rel}(A, \bar B) &= (\mathrm{exist}(A \cap B), \mathrm{exist}(\bar A \cap \bar B), \mathrm{exist}(A \cap \bar B), \mathrm{exist}(\bar A \cap B)) \\ &= (c, o, l, r) \\ \mathrm{rel}(\bar A, B) &= (\mathrm{exist}(\bar A \cap \bar B), \mathrm{exist}(A \cap B), \mathrm{exist}(\bar A \cap B), \mathrm{exist}(A \cap \bar B)) \\ &= (o, c, r, l) \\ \mathrm{rel}(\bar A, \bar B) &= (\mathrm{exist}(\bar A \cap B), \mathrm{exist}(A \cap \bar B), \mathrm{exist}(\bar A \cap \bar B), \mathrm{exist}(A \cap B)) \\ &= (r, l, o, c) \\ \end{aligned}

となる。すなわち、 \mathrm{rel}(A, B) が求まれば \mathrm{rel}(A, \bar B), \mathrm{rel}(\bar A, B), \mathrm{rel}(\bar A, \bar B), \mathrm{rel}(B, A), \mathrm{rel}(B, \bar A), \mathrm{rel}(\bar B, A), \mathrm{rel}(\bar B, \bar A) が求まるということである。

1-8. スーパータイプ・サブタイプの関係から二項関係の構築

以下が成り立つ。

l = \mathrm{false} \iff A \subseteq B \\ r = \mathrm{false} \iff A \supseteq B

したがって、 c および o が求まれば、 \mathrm{rel}(A, B) が求まることになる。
ここで、

\mathrm{ext}(A) \le 1 \land \mathrm{ext}(B) \le 1

のとき、

A \cup B \ne \top

であることから、

\begin{aligned} Outside &= \bar A \cap \bar B \\ &= \lnot(A \cup B) \\ &\ne \bot \\ o &= \mathrm{true} \end{aligned}

が成立する。

また、

\bar A \supseteq B

のとき、

B \setminus \bar A = B \cap \lnot \bar A = B \cap A = \bot

なので、

c = \mathrm{false}

が成立する。

よって、 \mathrm{ext}(A) \le 1 \land \mathrm{ext}(B) \le 1 のとき、

\mathrm{rel}(A, B) = (!(A \subseteq B), !(A \supseteq B), !(\bar A \supseteq B), \mathrm{true})

で求めることができる。

\mathrm{ext}(A) \ge 2 \lor \mathrm{ext}(B) \ge 2 のときは、 \mathrm{rel}(\bar A, B), \mathrm{rel}(A, \bar B), \mathrm{rel}(\bar A, \bar B) のいずれかを求めてから1-7で求めたように項の入れ替えを行えば良い。