流動性供給プールの自動リバランスにおいてポーション価値が増大する条件

はじめに

この記事は仮想通貨などの運用として、流動性プールに供給したポーションがAMMの自動リバランスによって価値が増える場合と減る場合の条件に付いて、数字に弱い筆者が考えをまとめるために数式を伴って書いた記事です。知っている人にとっては当たり前のことが書いてあると思います。

インパーマネントロス

流動性供給プールに通貨をペアで預け入れた際によく言及されるのがインパーマネントロスです。これは、通貨のレートの変動によって、預け入れなかった場合であれば被ることのなかった損失が発生することを指します。要するに機会損失を生むというわけです。

しかし、筆者のような弱小トレーダーにとっては通貨をずっと持っていたところで交換するタイミングを掴めず、考えなしのガチホ戦略を行い、損失するところの機会なんてそもそも持っていなかったりします。

そこで再考するのが流動性プールにおけるリバランスです。
流動性プールは価格変動が起こった際、アルゴリズムによって自動的に売買を行い、その通貨ペアの供給バランスを1:1に保とうとします。価格に変動が起これば、高い方の通貨の割合が減って、安い通貨を買い増します。

このような売買戦略は、「予め割合を決めておき、それより高くなれば利確し、またそれより低くなれば損切し、リバランスする」という分散投資としては基本的な買い方です。

なので、トレーディングをこの売買アルゴリズムに任せる + スワップ利率を得るという戦略は、トレーディング初心者にとっては有効なのではないかと考えたわけです。

しかしその場合、利益がでるのはどういう条件なのでしょうか？
筆者はよくわからなかったので数式を用いて考えてみることにします。

資産の方程式

まず、リキッドプールの流動性$N$は、通貨ペアのそれぞれの保有量を$A,B$としたとき、このような数で表されます。

$$\tag{1} A \times B = N (一定)$$

例えばETHを10、DAIを1000持っていた場合、$N=10000となるわけです。$

また、この時それぞれのトークンの価値の合計は1:1です。ドル建てでも円建てでもいいですが、その時のトークンAのレートを$R_a$、トークンBのレートを$R_b$とすると、こうですね。

$$\tag{2} A R_a = B R_b$$

主にこれらの特徴から性質を導いていきます。
さて今回僕が気になっているのが、トークンの価値が変動したあと、自分が供給した分の資産はどういう条件で増え、どういう条件で減るのかという話です。なので、変動後の資産を$S_1$、最初の資産を$S_0$とすると下記のようになります。変動後のトークン量と変動後のレートをそれぞれダッシュをつけて表しています。

$$S_0 = A R_a + B R_b$$

$$S_1 = A^\prime R^\prime_a + B^\prime R^\prime_b$$

したがいまして増分$S_d$はこうですね

$$S_d = S_1 - S_0$$

この$S_d$を詳しく見ていきましょう。まず、増加後のトークン量と元のトークン量の比を$k_a$,$k_b$とすると

$$\begin{aligned} A' = k_aA \\ B' = k_bB \end{aligned}$$

と表せます。また、(1)式より、

$$\begin{aligned} N &= A \times B \\ &= A' \times B' \\ &= k_aA \times k_b B \end{aligned}$$

であるので、

$$\tag{3} \begin{aligned} A \times B &= k_aA \times k_b B \\ 1 &= k_a k_b \\ k_b &= \frac{1}{k_a} \end{aligned}$$

ですね。この$k_a$を今後は$k$と書くことにします。すなわち、$k_a = k, k_b = \frac{1}{k}$です。

次にレートの変動についてみていきましょう。変動後のレートと最初のレートの比をjで表します。

$$R'_a = j_a R_a \\ R'_b = j_b R_b$$

すると、(2)より

$$\begin{aligned} A'R'_a &= B'R'_b \\ kAj_aR_a &= \frac{1}{k}Bj_b R_b \\ k &= \sqrt{\frac{Bj_bR_b}{Aj_aR_a}} \\ \end{aligned}$$

ここで、(2)を適用して約分すると

$$\begin{aligned} \tag{4} k &= \sqrt{\frac{j_b}{j_a}} \end{aligned}$$

となりますね。

$$\begin{aligned} S_d &= S_1 - S_0 \\ &= A'R'_a + B'R'_b - A R_a - B R_b \\ &= 2 kA j_aR_a - 2 A R_a \\ &= 2AR_a(kj_a - 1) \end{aligned}$$

ということで、$kj_a - 1$が正かどうかで資産が増大しそうです。$F=kj_a - 1$とおいて、この関数を調べましょう。(4)式を活用すると、下記のようになります。

$$\begin{aligned} F(j_a, j_b) &= k j_a -1 \\ &= \sqrt{j_a j_b}-1 \\ \end{aligned}$$

だんだん紐解かれてきた感じがします。
$j_a$と$j_b$はレートが何倍になったかを表す数字だったので、それらの相乗平均が1より大きければ資産は増大するということですね。

仮にステイプル通貨などで片方のレートが固定されていたとすると、

$$F(x) = \sqrt{x} - 1$$

となり、このグラフは

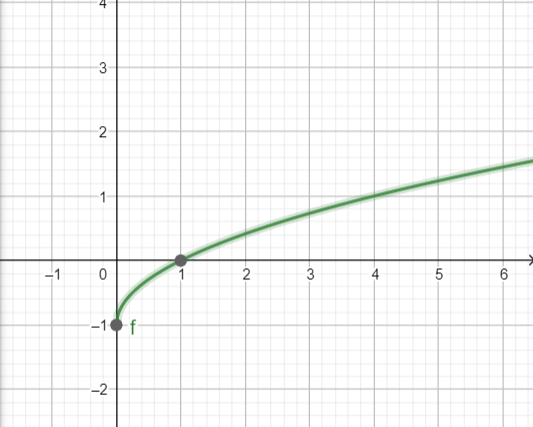
となります。レートの変動比が1より大きければ増大するということですね（当たり前だろ）

終わりに

結論としては、通貨ペアのそれぞれの価格変動の比の相乗平均が1より大きければ資産は増大する、というとても普通の結論でした。当たり前のことに気づけなかった......。
相乗平均が普段の生活でそんなに出てこないので気づけなかったのかもしれません。こんなんで仮想通貨に手を出していいのか！？

ここまで読んでくれてありがとうございます。
間違っているところとか分かりにくいところがあればコメントしてください。