LSTMとLightGBMを用いた時系列分析
概要
今回は、時系列データにおける異常検知を目的としLSTMとLightGBMの動作確認を行います。どちらも時系列データの分析に使われる手法ですが、それぞれの特徴や動作の違いを実感しながら進めていきます。
前提条件
まず、LSTMとLightGBMを実行する環境をMac M1に用意しました。tensorflowとlightgbmのバージョンは以下の通りです。
import tensorflow as tf; print(tf.__version__)
2.12.0
import lightgbm as lgb; print(lgb.__version__)
4.5.0
使用するデータはTensorFlow公式ページの時系列データセットをローカルにダウンロードしたものです。
LSTM
準備
まずはLSTMモデルを使った時系列データの解析を行います。LSTM(Long Short-Term Memory)は、長期間の依存関係を学習するために特化したRNN(リカレントニューラルネットワーク)であり、特に時系列データの予測に有効です。
必要なライブラリをインポートします。
import pandas as pd
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense, Dropout
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
データの前処理
データセットを読み込んだ後、今回は計算の負荷を軽減するため、温度と湿度の2つの特徴量に絞って正規化します。今回は動作確認を目的としているため、実際の用途では必ずしもこのような圧縮が有効とは限りません。しかしながら、高次の周波数はノイズに類するものもあり、MAやEMAで除去したほうが精度が上がる場合もあります。FFTなどで確認して除去することもあるかと思います。
# データの読み込みと前処理
data = pd.read_csv('jena_climate_2009_2016.csv') # DLしたファイル名
n_rows = len(data)
data = data[:n_rows // 3] # データセットが大きいので最初の1/3の期間を選択
# 使う特徴量を指定
features = ['T (degC)', 'rh (%)'] # 2つのコラムに絞る
data = data[features]
# データの正規化
scaler = MinMaxScaler()
data_scaled = scaler.fit_transform(data)
データが次のようにスケーリングされました。
data_scaled,data_scaled.shape
----
(array([[0.25876057, 0.92303274],
[0.25202831, 0.9241815 ],
[0.25030209, 0.92992533],
...,
[0.64854134, 0.60011488],
[0.65648196, 0.59368179],
[0.66839289, 0.56680069]]),
(140183, 2))
時系列データのウィンドウ化と分割
次に、データをウィンドウ化して、トレーニング、検証、テスト用に分割します。
# 時系列データのウィンドウ化
def create_dataset(data, time_step=5):
X, y = [], []
for i in range(len(data) - time_step):
X.append(data[i:(i + time_step), :])
y.append(data[i + time_step, 0]) # 例えば気温('T (degC)')を予測する
return np.array(X), np.array(y)
time_step = 12 # 12ステップで予測
X, y = create_dataset(data_scaled, time_step)
# データの形状確認
print(X.shape) # (サンプル数, タイムステップ数, 特徴量数)
# データの分割(同じ)
train_size = int(len(X) * 0.7)
val_size = int(len(X) * 0.2)
X_train, X_val, X_test = X[:train_size], X[train_size:train_size + val_size], X[train_size + val_size:]
y_train, y_val, y_test = y[:train_size], y[train_size:train_size + val_size], y[train_size + val_size:]
----
(140171, 12, 2)
モデルの構築
LSTM層を使用して、モデルを構築します。
各層についての構成について補足します。この構成は経験則によるもので、必ずこれが正解というものはありませんが、一般的には複数の層がある方が事象を深く捉えるとされており、1層目のLSTMが各タイムステップの情報を捉え、次の層にそれを渡すと、2層目のLSTMは前の層で得た出力をもとに、さらに詳細な時系列依存関係を学習します。深くすれば計算コストも増加しますし、重みが定まらず局所解に陥る可能性も上がってしまうため、必ずしも層を多くすれば良い結果が得られるというものでもありません。
1. LSTM(50, return_sequences=True)
最初のLSTM層は、ユニット数が50で、return_sequences=Trueとなっています。これにより、各タイムステップの隠れ状態の出力が次の層に渡されます。この設定は、複数のLSTM層を積み重ねる際に必要です。LSTM層がもう1つ続くため、すべてのタイムステップの出力を次のLSTM層に入力するためにreturn_sequences=Trueが指定されています。ユニット数50は、計算コストを考えこの程度としています。
2. Dropout(0.2)
次に配置されているドロップアウト層は、過学習を防ぐために20%のユニットを無作為に無効化します。LSTMは非常に多くのパラメータを持つため、過学習しやすいモデルです。そのため、ドロップアウト層を用いることで汎化性能を高めます。
3. LSTM(50, return_sequences=False)
2つ目のLSTM層も1層目と同様に50ユニットを持っていますが、return_sequences=Falseとなっています。これにより、この層では最後のタイムステップの出力のみを次の層に渡します。最終的には1つの予測値(次のステップの気温)を出力するため、ここではタイムステップごとの出力が不要になるためです。
4. Dropout(0.2)
再度、ドロップアウト層が挿入されています。こちらも同様に過学習を抑えるためで、モデル全体の汎化性能を向上させる目的です。
5. Dense(25)
この全結合層(Dense層)は、次の出力層に渡すために、さらに抽象的な表現を学習させます。25ユニットを持つこの層は、LSTMの隠れ状態からの出力を受け取り、次の層へと情報を凝縮して渡します。
6. Dense(1)
最後の全結合層は、1つの値(次のタイムステップの気温)を出力します。このモデルでは1ステップ先の気温を予測するため、この1つのユニットが最終的な予測結果となります。
公式のリファレンスはこのあたりを確認することになります。
コンパイルの最適化オプションにadam、ロスの評価としてMSEを選択しています。 Adam(Adaptive Moment Estimation) は、学習率を自動調整し、勾配の変動に強く、安定した学習を高速に行えるため、MSE(Mean Squared Error、平均二乗誤差) は、大きな誤差に対してペナルティを強くし、連続値を正確に予測することが求められる時系列予測問題において、モデルの性能を最大限に引き出すために合理的な組み合わせです。
# モデルの構築
model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(X_train.shape[1], X_train.shape[2])))
model.add(Dropout(0.2))
model.add(LSTM(50, return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(25))
model.add(Dense(1))
model.summary()
# モデルのコンパイル
model.compile(optimizer='adam', loss='mean_squared_error')
----
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, 12, 50) 10600
dropout (Dropout) (None, 12, 50) 0
lstm_1 (LSTM) (None, 50) 20200
dropout_1 (Dropout) (None, 50) 0
dense (Dense) (None, 25) 1275
dense_1 (Dense) (None, 1) 26
=================================================================
Total params: 32,101
Trainable params: 32,101
Non-trainable params: 0
トレーニング
今回はバッチサイズ64、エポック数10でモデルをトレーニングします。
# モデルのトレーニング
history = model.fit(X_train, y_train, validation_data=(X_val, y_val), epochs=10, batch_size=64, verbose=1)
model.save('./jena_climate_T.h5')
----
Epoch 1/10
1534/1534 [==============================] - 39s 23ms/step - loss: 0.0020 - val_loss: 1.0995e-04
Epoch 2/10
1534/1534 [==============================] - 27s 17ms/step - loss: 1.3797e-04 - val_loss: 7.1949e-05
Epoch 3/10
1534/1534 [==============================] - 27s 17ms/step - loss: 9.9945e-05 - val_loss: 9.6458e-05
Epoch 4/10
1534/1534 [==============================] - 29s 19ms/step - loss: 8.0154e-05 - val_loss: 4.3426e-05
Epoch 5/10
1534/1534 [==============================] - 29s 19ms/step - loss: 6.2440e-05 - val_loss: 4.9105e-05
Epoch 6/10
1534/1534 [==============================] - 31s 20ms/step - loss: 5.3762e-05 - val_loss: 1.1244e-04
Epoch 7/10
1534/1534 [==============================] - 27s 18ms/step - loss: 4.4778e-05 - val_loss: 2.6847e-05
Epoch 8/10
1534/1534 [==============================] - 28s 18ms/step - loss: 3.6424e-05 - val_loss: 2.3503e-05
Epoch 9/10
1534/1534 [==============================] - 28s 18ms/step - loss: 3.3309e-05 - val_loss: 6.1341e-05
Epoch 10/10
1534/1534 [==============================] - 29s 19ms/step - loss: 3.1598e-05 - val_loss: 3.2214e-05
モデルの評価
次に、トレーニング、検証、テストデータに対してモデルの評価を行います。
# モデルの評価
train_predict = model.predict(X_train)
val_predict = model.predict(X_val)
test_predict = model.predict(X_test)
----
3067/3067 [==============================] - 17s 5ms/step
877/877 [==============================] - 4s 5ms/step
439/439 [==============================] - 2s 4ms/step
----
test_predict.shape,val_predict.shape,train_predict.shape
----
((14018, 1), (28034, 1), (98119, 1))
データを元のスケールに戻して予測値を評価します。
# データを元のスケールに戻す
train_predict = scaler.inverse_transform(np.concatenate([train_predict, np.zeros((train_predict.shape[0], data.shape[1] - 1))], axis=1))[:,0]
val_predict = scaler.inverse_transform(np.concatenate([val_predict, np.zeros((val_predict.shape[0], data.shape[1] - 1))], axis=1))[:,0]
test_predict = scaler.inverse_transform(np.concatenate([test_predict, np.zeros((test_predict.shape[0], data.shape[1] - 1))], axis=1))[:,0]
y_train_inv = scaler.inverse_transform(np.concatenate([y_train.reshape(-1, 1), np.zeros((y_train.shape[0], data.shape[1] - 1))], axis=1))[:,0]
y_val_inv = scaler.inverse_transform(np.concatenate([y_val.reshape(-1, 1), np.zeros((y_val.shape[0], data.shape[1] - 1))], axis=1))[:,0]
y_test_inv = scaler.inverse_transform(np.concatenate([y_test.reshape(-1, 1), np.zeros((y_test.shape[0], data.shape[1] - 1))], axis=1))[:,0]
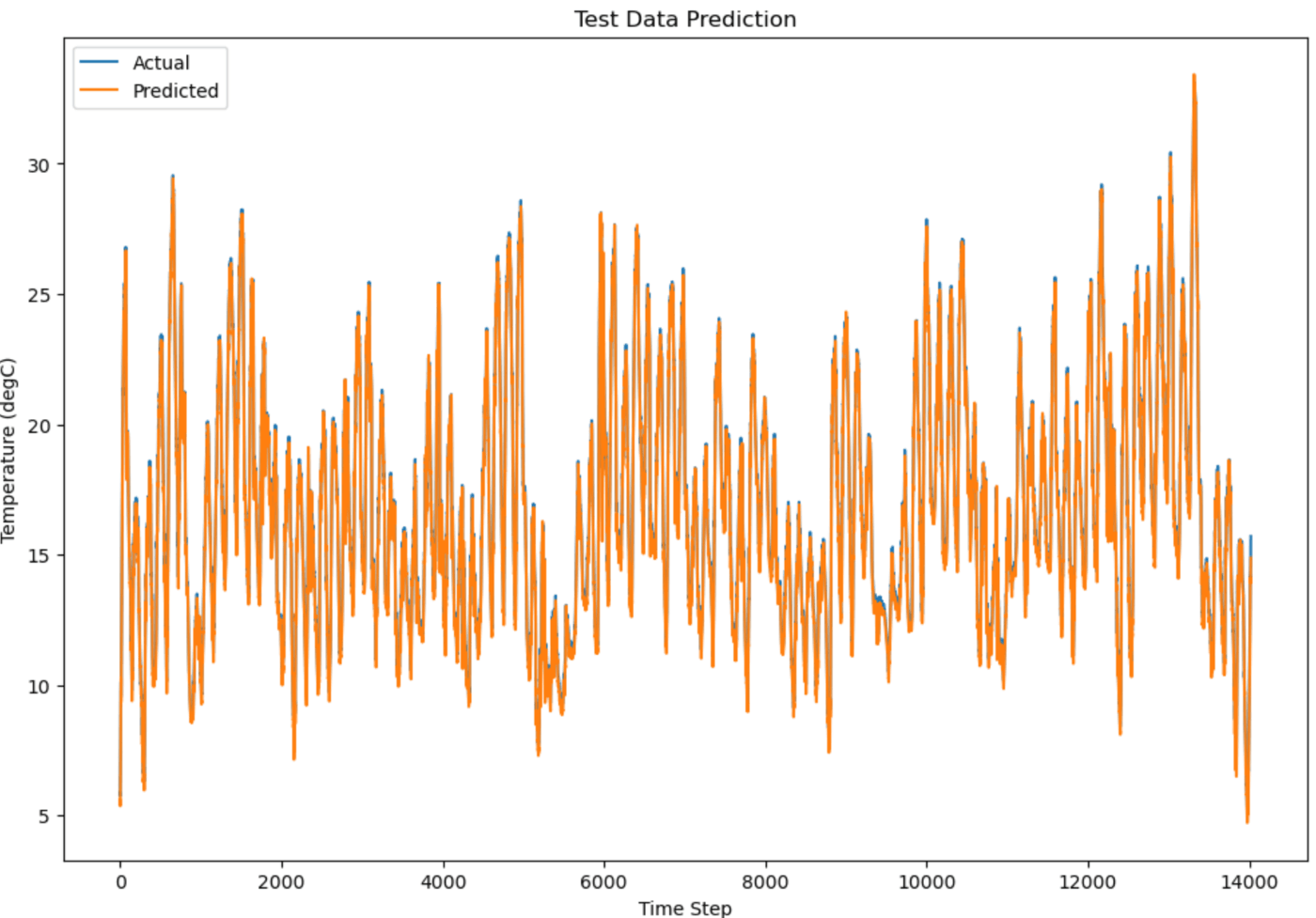
LSTMの結果としては、テストデータに対してのRMSEは0.376となりました。ロスの履歴と、testデータを用いた予測を表示します。
RMSE(Root Mean Squared Error) は、モデルの予測誤差を評価する指標です。誤差を二乗して平均し、その平方根を取るため、大きな誤差に敏感です。値が小さいほど、モデルの予測が実際の値に近く、精度が高いことを意味します。
# エラープロット
plt.figure(figsize=(12,8))
plt.plot(y_test_inv, label='Actual')
plt.plot(test_predict, label='Predicted')
plt.title('Test Data Prediction')
plt.xlabel('Time Step')
plt.ylabel('Temperature (degC)')
plt.legend()
plt.show()
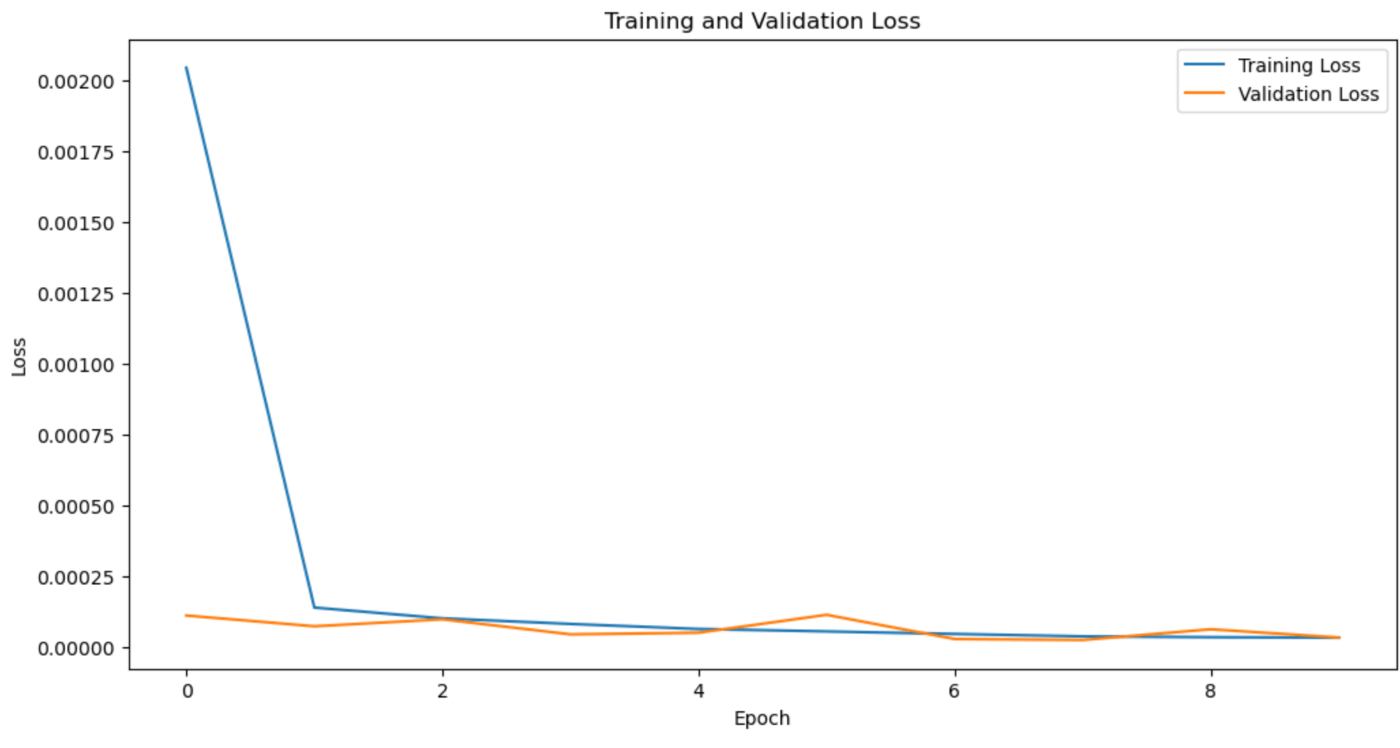
# 損失のプロット
plt.figure(figsize=(12,6))
plt.plot(history.history['loss'], label='Training Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.show()
# RMSEの計算
from sklearn.metrics import mean_squared_error
import math
train_rmse = math.sqrt(mean_squared_error(y_train_inv, train_predict))
val_rmse = math.sqrt(mean_squared_error(y_val_inv, val_predict))
test_rmse = math.sqrt(mean_squared_error(y_test_inv, test_predict))
print(f'Training RMSE: {train_rmse}')
print(f'Validation RMSE: {val_rmse}')
print(f'Test RMSE: {test_rmse}')
----
Training RMSE: 0.3484714066792065
Validation RMSE: 0.32879634823804754
Test RMSE: 0.3762445000460043
グラフィカルには、わりと良い予測結果が得られているように思えます。
EPOCの2サイクル目以降については、本モデル構成においては精度がそれほど上がらないように見えます。数倍のEPOCにして長期の学習遷移については確認しておりません。
LightGBM
LSTMは、時系列データの特徴を捉えるのに適していますが、計算コストが高く、学習に時間がかかるため、特にリアルタイムのアプリケーションには向かない場合があります。そこで、マイクロソフトが公開する軽量高速なモデルであるLightGBM(Light Gradient Boosting Machine)を用いて同じ時系列データに対する予測を行い、LSTMと比較してみます。
LightGBMは、勾配ブースティングアルゴリズムに基づく決定木ベースの学習手法で、複数の決定木を段階的に組み合わせて予測精度を高めます。高速な学習と予測性能の高さが特徴で、大規模データや高次元データに対しても有効です。
使用ライブラリの読み込みとデータの準備
まず、必要なライブラリを読み込み、LSTMと同様にデータを前処理します。LightGBMは必ずしもデータの正規化を必要としませんが、LSTMとの比較を行うため、同じ正規化を行います。
import pandas as pd
import numpy as np
import lightgbm as lgb
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# データの読み込みと前処理 (LSTMの準備部分と同じ)
features = ['T (degC)', 'rh (%)'] # 2つのコラムに絞る
data = data[features]
# データの正規化(LightGBMは必ずしも正規化を必要としませんが、一貫性のためにLSTMと同様に行います)
scaler = MinMaxScaler()
data_scaled = scaler.fit_transform(data)
時系列データのウィンドウ化
次に、LSTMと同様に、データをウィンドウ化し、ステップに分割してモデルの入力データを作成します。LightGBMでは2次元の入力データが必要なため、LSTMで使用した3次元データを2次元に変換します。
# 時系列データのウィンドウ化(LSTMと同様に行います)
def create_dataset(data, time_step=5):
X, y = [], []
for i in range(len(data) - time_step):
X.append(data[i:(i + time_step), :])
y.append(data[i + time_step, 0]) # 気温('T (degC)')を予測する
return np.array(X), np.array(y)
time_step = 12 # 12ステップで予測
X, y = create_dataset(data_scaled, time_step)
# 2Dに変形(LightGBMは2次元データを扱うので、特徴量を1つの次元にまとめます)
X = X.reshape(X.shape[0], -1)
# データの分割
train_size = int(len(X) * 0.7)
val_size = int(len(X) * 0.2)
X_train, X_val, X_test = X[:train_size], X[train_size:train_size + val_size], X[train_size + val_size:]
y_train, y_val, y_test = y[:train_size], y[train_size:train_size + val_size], y[train_size + val_size:]
LSTMでは、時系列データを3次元の形状(サンプル数、タイムステップ数、特徴量数)で処理しますが、LightGBMでは2次元の入力データ(サンプル数、全特徴量)に変換して処理します。ここでは、12ステップのデータを次のステップの気温を予測するために使用しています。
モデルの構築とトレーニング
LightGBMのモデルを構築し、学習を行います。LightGBMのトレーニングは、非常に高速であるため、大規模データやリアルタイム処理に向いています。また、トレーニング時にはearly_stoppingを使用して、一定期間改善が見られなかった場合にトレーニングを自動的に終了させます。
Datasetの内容はこちらにリファレンスがあります。
学習パラメータのリファレンスはこちらにありますが、非常にたくさんのパラメータがありますので目的に合わせて選定が必要です。今回は、大凡をデフォルトで設定しています。
objective: モデルの目的を指定します。今回は回帰問題を解決するために'regression'を指定しています。
metric: モデルの性能を評価するための指標を指定します。ここでは'rmse'(Root Mean Squared Error)を指定しています。学習中にモデルの性能が評価され、早期終了やパラメータ調整に利用されます。
boosting_type: ブースティングの手法を指定します。ここでは一般的な決定木ブースティングである'gbdt'を指定しています。ブースティングの種類により、学習の効率や精度、過学習のリスクが異なります。他にも'dart'や'goss'などの選択肢があります。
learning_rate: 学習率は、各ステップでモデルの重みを更新する際の調整幅を示します。ここでは0.01に設定されています。 小さな値を選ぶことで、モデルはより慎重に学習し、過学習のリスクを低減できますが、学習に時間がかかる可能性もあります。
num_leaves: 決定木の葉の数を指定します。ここでは31に設定しています。多すぎると過学習を引き起こすリスクがありますが、少なすぎるとモデルの表現力が不足し、アンダーフィッティングを引き起こす可能性があります。一般的に、2の冪数を選ぶことが推奨されます。
verbose : ログ出力の詳細度を指定します。1以上を指定することで詳細なログを取得することが可能となります。今回設定している-1は出力を抑制することを意味します。
# LightGBM用のデータセット
train_data = lgb.Dataset(X_train, label=y_train)
val_data = lgb.Dataset(X_val, label=y_val, reference=train_data)
# パラメータ設定
params = {
'objective': 'regression',
'metric': 'rmse',
'boosting_type': 'gbdt',
'learning_rate': 0.01,
'num_leaves': 31,
'verbose': -1
}
# モデルのトレーニング
model_lgb = lgb.train(params, train_data, valid_sets=[train_data, val_data], num_boost_round=1000,# 最大学習サイクル数
callbacks=[lgb.early_stopping(100)],
#verbose_eval=100
)
----
Training until validation scores don't improve for 100 rounds
Did not meet early stopping. Best iteration is:
[999] training's rmse: 0.0041982 valid_1's rmse: 0.00398879
ここでは、objectiveとして回帰問題を設定し、評価指標としてRMSEを使用しています。また、num_boost_roundを1000に設定していますが、early_stoppingにより改善が見られなければ100回目で停止する設定です。
モデルの評価
学習したモデルを用いてテストデータに対する予測を行い、LSTMと同様にRMSEを用いて精度を評価します。
# 予測
train_predict_lgb = model_lgb.predict(X_train, num_iteration=model_lgb.best_iteration)
val_predict_lgb = model_lgb.predict(X_val, num_iteration=model_lgb.best_iteration)
test_predict_lgb = model_lgb.predict(X_test, num_iteration=model_lgb.best_iteration)
# スケーリングを元に戻す
train_predict_lgb = scaler.inverse_transform(np.concatenate([train_predict_lgb.reshape(-1, 1), np.zeros((train_predict_lgb.shape[0], data.shape[1] - 1))], axis=1))[:, 0]
val_predict_lgb = scaler.inverse_transform(np.concatenate([val_predict_lgb.reshape(-1, 1), np.zeros((val_predict_lgb.shape[0], data.shape[1] - 1))], axis=1))[:, 0]
test_predict_lgb = scaler.inverse_transform(np.concatenate([test_predict_lgb.reshape(-1, 1), np.zeros((test_predict_lgb.shape[0], data.shape[1] - 1))], axis=1))[:, 0]
y_train_inv = scaler.inverse_transform(np.concatenate([y_train.reshape(-1, 1), np.zeros((y_train.shape[0], data.shape[1] - 1))], axis=1))[:, 0]
y_val_inv = scaler.inverse_transform(np.concatenate([y_val.reshape(-1, 1), np.zeros((y_val.shape[0], data.shape[1] - 1))], axis=1))[:, 0]
y_test_inv = scaler.inverse_transform(np.concatenate([y_test.reshape(-1, 1), np.zeros((y_test.shape[0], data.shape[1] - 1))], axis=1))[:, 0]
# 評価指標 (RMSE) の計算
train_rmse_lgb = np.sqrt(mean_squared_error(y_train_inv, train_predict_lgb))
val_rmse_lgb = np.sqrt(mean_squared_error(y_val_inv, val_predict_lgb))
test_rmse_lgb = np.sqrt(mean_squared_error(y_test_inv, test_predict_lgb))
print(f'LightGBM Training RMSE: {train_rmse_lgb}')
print(f'LightGBM Validation RMSE: {val_rmse_lgb}')
print(f'LightGBM Test RMSE: {test_rmse_lgb}')
-----
LightGBM Training RMSE: 0.2432015388606122
LightGBM Validation RMSE: 0.23107063356473306
LightGBM Test RMSE: 0.27658140877143433
ここでは、LSTMと同様に RMSE(Root Mean Squared Error) を計算し、予測結果と実際のデータとの差を評価します。RMSEが小さいほど予測の精度が高いことを示しています。
結果の可視化
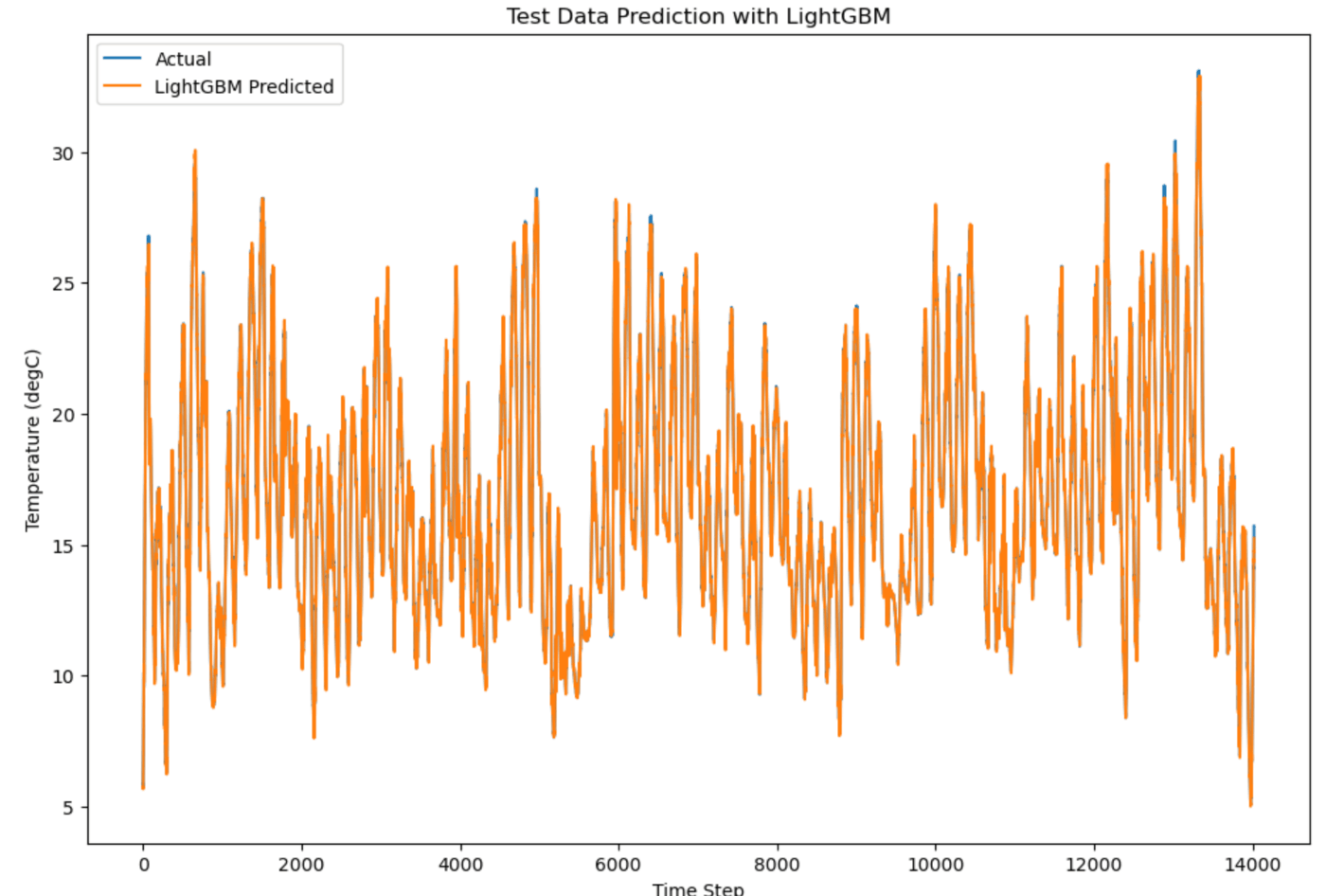
最後に、テストデータに対する実際の値とLightGBMの予測結果を比較し、プロットで視覚的に確認します。
#結果のプロット
plt.figure(figsize=(12,8))
plt.plot(y_test_inv, label='Actual')
plt.plot(test_predict_lgb, label='LightGBM Predicted')
plt.title('Test Data Prediction with LightGBM')
plt.xlabel('Time Step')
plt.ylabel('Temperature (degC)')
plt.legend()
plt.show()
まとめ
今回の結果では、LSTMよりもLightGBMの方が良い性能を示しました。LightGBMはテストデータに対してより低いRMSEを達成していますが、必ずしもどちらかが優れる精度が得られるというわけではなくケースにより使い分けが必要です。LSTMは長期の依存関係を扱える強力なモデルですが、トレーニングに時間がかかり、計算リソースを多く必要とします。一方で、LightGBMは軽量かつ高速であり、リアルタイム処理に適しています。
Discussion