🗂

Vector Search:４つのベクトル検索アルゴリズム：コサイン類似度、ユークリッド距離、マンハッタン距離、負の内部積（スカラー積）

2024/05/16に公開

前回の記事ではVector Searchはコサイン類似度、ユークリッド距離の検索に対応していると記載しました。
https://zenn.dev/kameping
PingCAPの方の記事を見ているともう２つ、マンハッタン距離、負の内部積（スカラー積）にも対応していることがわかりましたので、（無謀にも！？）まとめたいと思います。

前回のおさらい

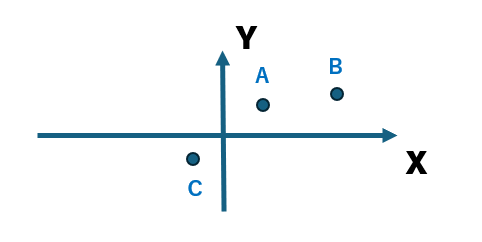
こちらの図を参考に、ユークリッド距離ではAとCが近く、コサイン類似度ではAとBが近しいと解説を行いました。

コサイン類似度

SELECT embedding, vec_cosine_distance(embedding, '[1,1]') AS d FROM vector_table ORDER BY d;
+-----------+--------------------+
| embedding | d                  |
+-----------+--------------------+
| [4,1]     | 0.1425070742874559 |
| [-1,-1]   |                  2 |
+-----------+--------------------+
2 rows in set (0.26 sec)

ユークリッド距離

SELECT embedding, vec_l2_distance(embedding, '[1,1]') AS d FROM vector_table ORDER BY d;
+-----------+--------------------+
| embedding | d                  |
+-----------+--------------------+
| [-1,-1]   | 2.8284271247461903 |
| [4,1]     |                  3 |
+-----------+--------------------+
2 rows in set (0.25 sec)

マンハッタン距離

マンハッタン距離はユークリッド距離と似ていますが、直線上の距離ではなく以下のような計算を行います。

マンハッタン距離

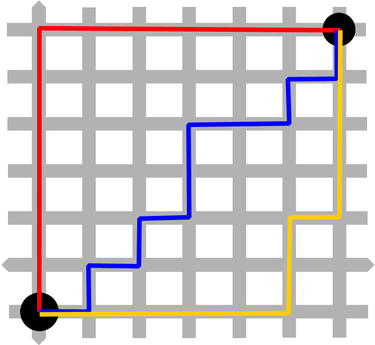
SELECT embedding, vec_l1_distance(embedding, '[1,1]') AS d FROM vector_table ORDER BY d;
+-----------+------+
| embedding | d    |
+-----------+------+
| [4,1]     |    3 |
| [-1,-1]   |    4 |
+-----------+------+
2 rows in set (0.25 sec)

RAGで用いる場合、複数の概念が交差するケースで高い精度を出すようです。例えばとあるコンセプトが別のコンセプトの中でどう取り扱われているか？等です。ある検索結果をさらに次の検索に用いるなどもそれに相当します。

負の内部積（負のスカラー積）

まず、スカラー積から。
スカラー積は二つのベクトルの掛け算です。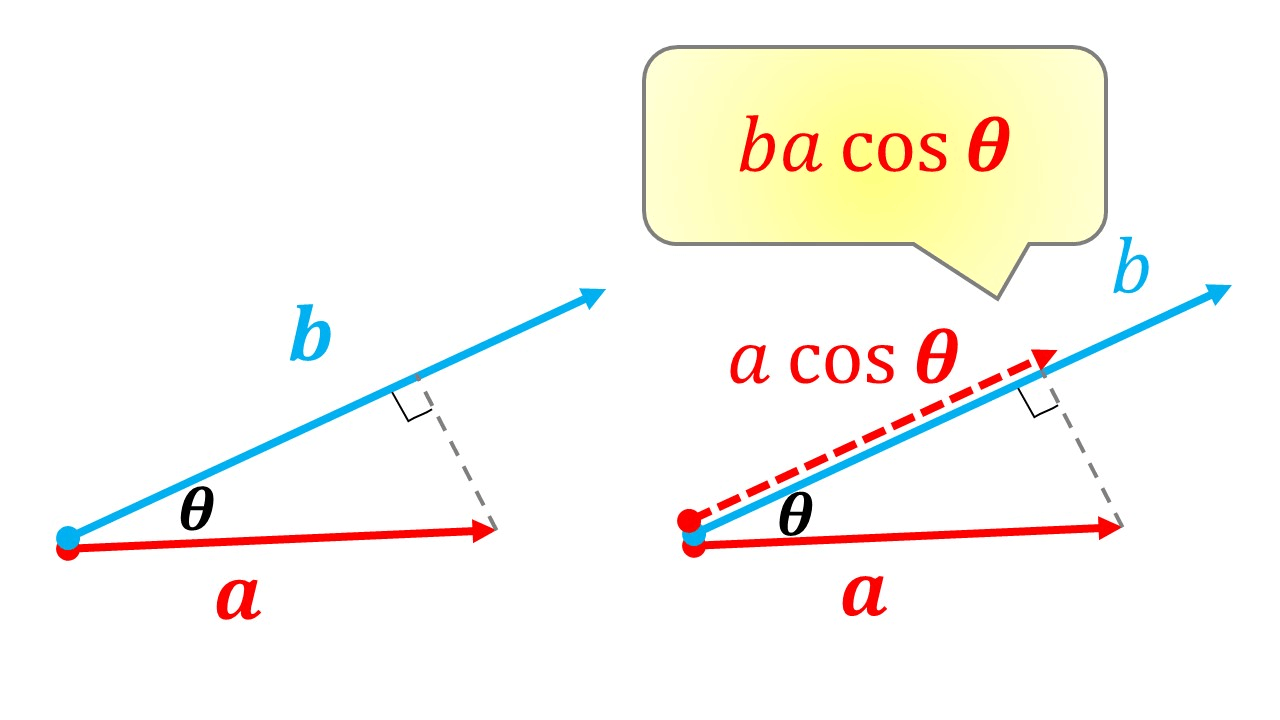

aの長さをbと揃えるとacosΘになります。acosΘ*bがスカラー積です。
例えばシンプルな以下の図の場合

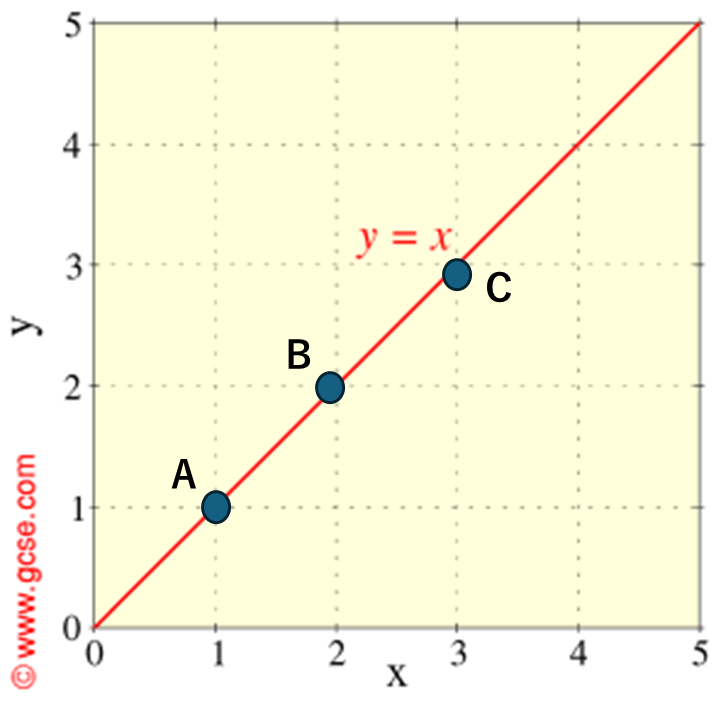
AからするとBとCのコサイン類似度は同じです。同じ直線上にあります。一方スカラー積ではAC＞ABです。つまりACの方がより強くその傾向を示すとも言えます。例えばレコメンドエンジンの場合、ACの方がより強く趣味の傾向を表す行動をとりやすいユーザーと言えます。
この逆が負のスカラー積です。例えばニュースについての分析を行う場合、多様な視点からの情報を取り込む場合などに有益です。QAなども同様に複数の過去の問い合わせ結果を多面的に取り込むことでより質の高い回答が可能となります。

負の内部積

SELECT embedding, vec_negative_inner_product(embedding, '[1,1]') AS d FROM vector_table ORDER BY d;
+-----------+------+
| embedding | d    |
+-----------+------+
| [4,1]     |   -5 |
| [-1,-1]   |    2 |
+-----------+------+
2 rows in set (0.25 sec)

とはいえ

４つご紹介しましたが、とはいえ何が役に立つかわかりません。Vector Searchを用いた場合簡単にアルゴリズムを変更できるので、結局のところ４つとも試すことをお勧めします。

前回のおさらい

マンハッタン距離

負の内部積（負のスカラー積）

とはいえ

Discussion