📝

現在最強のText-to-3Dモデル"ProlificDreamer"をちゃんと理解する

2023/05/29に公開

Text-to-3Dがアツい

最近かなりText-to-3Dモデルがアツくなってきました。昨年9月末に発表されたDreamFusionから急速に発展し、11月にはMagic3DやLatent-NeRF, 12月にはSJCやDream3D, 今年に入って3月にはFantasia3DやText2Room, 今月5月にはOpenAIのShap-E, Text2NeRFが発表されるなど、ちょうど1年ほど前のText-to-Imageモデルの盛り上がり方を彷彿とさせます。
※この記事は2023/5/29に執筆したものです

その中で、5/25に発表された ProlificDreamerが強すぎるというのがあります。
まずこれを見てください。一番右がProlificDreamerで生成された3Dモデルです。左３つの既存手法はどこかもっさりとしているのに対し、ProlificDreamerはまるでどの視点からみてもDalle-2で生成されたかのよう。DreamFusionから半年強でここまで進化してしまったことに驚嘆の念を抱きます。

他の生成結果を見てみても、どれもこれまででは考えられないほど高精細な3Dモデルが生成されています。右下の馬に乗った宇宙飛行士など、まさにDalle-2で生成される2D画像と同じくらい高いクオリティになっています。
ProlificDreamerのプロジェクトページには、より多くの生成された3Dモデルを動画で見ることができるので、ぜひ覗いてみてください。

このProlificDreamerは、これまでのText-to-3Dモデル使用していたSDSという手法を拡張し、 VSD (Variational Score Distillation) という手法を提案しています。これはかなりしっかりとした理論的背景に基づいており、今後のText-to-3Dモデルの新しい潮流となる可能性が高いため、今回は 「ProlificDreamerをちゃんと理解する」 という趣旨で記事を書いていきます。

拡散モデル再訪

拡散モデルも一応言葉の定義をメインに触れて行きます。
拡散モデルは統計力学に端を発する生成モデルであり、ランダムノイズから徐々に自然なデータになるように徐々にデノイズしていく生成モデルです。

Denoising Diffusion Probabilistic Modelsより引用
拡散モデルは二つのプロセスから成ります。まずforward process $\{q_t\}_{t\in [0,1]}$ ではデータセットのデータ $x_0 \sim q_0(x_0)$ に徐々にノイズを加えていく過程で、その逆のreverse process $\{p_t\}_{t\in [0,1]}$ は徐々にノイズを除去してデータを生成する過程です。forward processは $q_t(x_t | x_0) = \mathcal{N}(\alpha_t x_0, \sigma_t^2 I)$ で定義され、 $q_t(x_t) = \int q_t(x_t | x_0)q_0(x_0)dx_0$ です。また、reverse process は $x_t$ にかけられたノイズを推定するモデル $\epsilon_\phi (x_t, t)$ で構成され、これが真のノイズ $\epsilon$ を正しく推定するように学習します。正しく学習されると、この推定ノイズは次のようにスコア関数に近似できるようになります。

\nabla_{x_t}\log q_t(x_t) \approx \nabla_{x_t}\log p_t(x_t) \approx -\epsilon_\phi (x_t,t) / \sigma_t

これまでのText-to-3D

DreamFusionから始まる、これまでの2D画像の拡散モデルを用いたText-to-3Dモデルの大きな潮流の手法は、SDS (Score Distillation Sampling) という手法を用いていました。これは簡単に言うと、さまざまなカメラ視点でNeRFから画像をレンダリングし、それが入力テキストのcondition $y$ に沿ったものになるように、NeRFなどの3D表現のパラメタ $\theta$ を最適化していくものです。
↓こちらの動画で詳しく解説していますので、先にこちらをご覧になっていただくと理解が進むと思います
https://youtu.be/pJg4qY3hOzA

DreamFusionの論文より引用

まず前提として、学習済みのText-to-Imageモデル $p_t(x_t | y)$ が与えられており、ノイズ推定モデル $\epsilon_{\mathrm{pretrain}}(x_t, t, y)$ で定義されているとします。これを用いてNeRFを入力テキストに合わせて最適化していくのですが、あるカメラ視点 $c$ からのレンダリング画像を $g(\theta, c)$ とし、それにforward processでノイズ $\epsilon \sim \mathcal{N}(0,1)$ をかけてノイズ画像 $x_t=\alpha_t g(\theta, c) + \sigma_t \epsilon$ を作ります。その分布を $q_t^\theta(x_t | c)$ として、SDSでは以下の目的関数に沿って $\theta$ を最適化します。

この損失関数の勾配は以下のように計算できます（DreamFusionのappendix参照）

このロス勾配に沿って $\theta$ を最適化していくことで、text condition $y$ に沿った3D表現を獲得することができます。以下は実際にDreamFusionで生成された3Dモデルです。この時点でも多様な3Dモデルを生成できていることがわかります。

DreamFusionの論文より引用

しかし、SDSにはいくつかの問題があります。DreamFusionでは、 $\epsilon_{\mathrm{pretrain}}(x_t, t, y)$ を推定する際の、classifier free guidanceのscaleを100程度のかなり大きい値にしています。これは、各視点画像が入力テキスト $y$ に対して最も"典型的な"ものになるようにして、3次元的な一貫性を担保しやすくするためです。その反面、少しぼやけた3Dモデルになってしまったり、同じ入力テキストに対する多様性が失われるという問題があります。この問題を解決するためにSDSを理論的に拡張しようというのが、本論文で提案されているVSD (Variational Score Distillation) です。

VSD (Variational Score Distillation)

VSDの基本的な発想は、入力テキスト $y$ が与えられたとき、それに対応する3D表現の分布を考える必要があるのではないか、というものです。つまり、 $y$ に対する3D表現のパラメタ $\theta$ の分布 $\mu(\theta | y)$ を考えていきます。このとき、 $q_0^\mu(x_0 | y)$ をレンダリング画像の分布とし、 $p_0(x_0 | y)$ をText-to-Imageモデルの出力画像の分布とします。VSDの目的は、これら2つの分布のKL divergenceを最小化するパラメタ分布 $\mu$ を見つけることになります。

\min_\mu D_{KL}(q_0^\mu(x_0 | y) || p_0(x_0 | y))

これを直接最適化することは

p_0

があまりに複雑なので不可能ですが、拡散モデルの目的関数の導出の式展開に沿って考えれば、以下のように変形することができます。

このあたりの式変形はUnderstanding Diffusion Models: A Unified Perspectiveの論文が非常にわかりやすいので、興味があれば参照してみてください。

SDSは一つの $\theta$ のみを最適化しますが、VSDではその分布を最適化する形になります。また、このKL divergenceを最小化することが、 $q_0^\mu(x_0 | y)$ を学習済みText-to-Imageモデルで与えられる真の分布に近づけることと同値であるということがTheorem 1で述べられています。

Theorem 1 VSDの大域最適性
それぞれの $t>0$ に対して、

D_{KL} (q_t^\mu(x_t|y) || p_t(x_t|y)) = 0 \iff q_0^\mu(x_0|y)=p_0(x_0|y)

証明は以下

図中の式(13)は拡散モデルのforward process, これを用いて $q_t^\mu$ と $q_0^\mu$ の特性関数を式(14)で出している。式(14)は特性関数の性質と正規分布の特性関数を利用。式(15)も同様。最後に式(16)で特性関数の一意性を使って証明できる。

VSDの更新方法

概要を理解したい方向け

先に手法の全体図を見た方がわかりやすいと思います

行っていることは以下です。

$\{\theta^{(i)}\}_{i=1}^n$ を用意して、それを確率分布 $\mu(\theta | y)$ からサンプリングされた3D表現のパラメタと見なすことで、間接的に $\mu$ を表現（Figure 2のparticles of NeRF/Meshに対応）
学習時には $\{\theta^{(i)}\}_{i=1}^n$ からランダムに一つ選び、それを用いてランダムなカメラ視点でレンダリング（Algorithm 1の4行目）
レンダリング画像にノイズを付与し、それを学習済みText-to-Imageモデルに入れて推定ノイズ $\epsilon_{\mathrm{pretrain}}(x_t,t,y)$ を得る。また、LoRAでカメラパラメタ $c$ も条件として入力可能にしたText-to-Imageモデルで $\epsilon_\phi(x_t,t,c,y)$ を得る。これらを用いて $\theta$ を更新（Algorithm 1の5行目）
実際に加えたノイズ $\epsilon$ と $\epsilon_\phi(x_t,t,c,y)$ を見比べて、Text-to-ImageモデルをLoRA finetune （Algorithm 1の6行目）
これを繰り返して3D表現を学習

理論的にもある程度ちゃんと理解したい方向け

まず、最適な $\mu^*$ を求めるために、何かしらの生成モデルを別に用意して $\mu$ をそこからサンプリング可能な分布として定義することが考えられますが、計算コストがかなり増えるので現実的ではありません。

そこで本論文では、Particle-based variational inference (ParVI) という手法を用いて $\mu(\theta | y)$ を推定しています。ParVIはベイズ推論の近似手法の一つであり、複雑な分布をその代表となるパーティクル（粒子）を用いて近似し、そのパーティクルを変分推論によって更新していくことで、推論対象の分布を表現する手法です。
VSDでは最も単純に、パーティクルとして $\{\theta^{(i)}\}_{i=1}^n$ を用意し、現在の $\mu$ からサンプリングされる代表点を表すとします。目的は、各 $\theta^{(i)}$ が最終的に、理想的な分布 $\mu^*$ からサンプリングされたものになるように $\theta^{(i)}$ を更新していくことです。それを実現する方法が、Wasserstein gradient flowです。
その詳しい内容はAppendix Cに書かれているので、それを要約していきます。

まず、目的関数は前章で説明した通り、次の $\mathcal{E}[\mu]$ です。

ここで $\mathbb{W}_2(\Theta)$ は2-Wasserstein空間で、確率変数集合 $\Theta$ 上の確率分布の空間のうち、2-Wasserstein距離を計量として持つ空間ですが、本筋から逸れるのでここでは深く触れません。

これを最適化するために、Wasserstein gradient flowでは以下の更新式で時刻 $\tau$ に沿って $\mu_\tau$ を更新すれば良いことが知られています(Variational Wasserstein gradient flowなどより)

\frac{\partial \mu_\tau}{\partial \tau} = -\nabla_{\mathbb{W}_2} \mathcal{E}[\mu] = \nabla_\theta \cdot \left(\mu_\tau \nabla_\theta \frac{\delta \mathcal{E}[\mu_\tau]}{\delta\mu_\tau} \right)

また、この式はFokker-Planck方程式の一種と見なすことができ、これに対応するパーティクル $\theta$ の発展方程式は以下になります。

\frac{d \theta_\tau}{d \tau} = - \nabla_\theta \frac{\delta \mathcal{E}[\mu_\tau]}{\delta\mu_\tau}

Fokker-Planck方程式とLangevin方程式の関係

Langevin方程式

dx = A(x,t)dt + B(x,t)dW_t

と、Fokker-Planck方程式

\frac{\partial p(x,t)}{\partial t} = -\frac{\partial}{\partial x}(A(x,t)p(x,t)) + \frac{1}{2}\frac{\partial^2}{\partial x^2}(B(x,t)^2 p(x,t))

は等価であることが知られています。（FOKKER-PLANCK- AND LANGEVIN EQUATIONなどより）
今回の場合は $t=\tau$ , $x=\theta_\tau$ , $p(x,t)=\mu_\tau(\theta)$ に対応しており、 $B(x,t)=0$ の決定的な過程で、 $A(x,t)=-\nabla_\theta \frac{\delta \mathcal{E}[\mu_\tau]}{\delta\mu_\tau}$ とみなせます。
この辺の話は多分この資料とかがわかりやすいと思います（ごめんなさいちゃんと読んでないです）

これにより、 $\frac{\delta \mathcal{E}[\mu_\tau]}{\delta\mu_\tau}$ を地道に計算していけば良いことになりますが、結論から述べると次のようになります。

ここの式変形を地道に追ってみる

なかなか大変です

まずLemma 1, これはいいでしょう
Lemma 2.
- 式(20)の最初のイコールは $q_t^\mu(x_t | c,y)$ の定義から、次のイコールは $c$ が与えられているとき $q_0^\mu(x_0 | c,y)$ は $\mu(\theta | y)$ からサンプリングした $\theta$ に対して決定的に決まるためです。
Lemma 3.
- 式(23)はchain-ruleで展開。 $q_t^\mu$ は連続変数 $x_t$ に対する確率密度なので $x_t$ で積分する必要があることに注意
- 式(24)はLemma 1とLemma 2から
- 式(25)はそのまま, 式(26)は $q_{t_0}(x_t | x_0)$ のランダムな変数が $\epsilon$ であることから

ここまできたら本題の証明は次のようにできます

ここで、 $-\sigma_t \nabla_{x_t}\log p(x_t | y)$ は学習済みのText-to-Imageモデルによる推定ノイズ $\epsilon_{\mathrm{pretrain}}(x_t, t, y)$ で近似できます。また、 $-\sigma_t \nabla_{x_t}\log q_t^{\mu_\tau}(x_t |c, y)$ はカメラパラメタ $c$ を条件に含んでいることから、新しい別のノイズ推定モデル $\epsilon_\phi(x_t, t, c,y)$ から推定する必要があります。それをこの論文では、学習済みのText-to-ImageモデルにLoRAを適用したものが良かったと報告されています。LoRAのパラメタ $\phi$ は、通常の拡散モデルの損失関数を使ってNeRFの学習と同時に学習されます。

\phi \leftarrow \phi - \eta \nabla_\phi \mathbb{E}_{t,\epsilon} ||\epsilon_\phi(x_t,t,c,y) - \epsilon||_2^2

ちなみにカメラパラメタ $c$ は、2層MLPを通してU-Netのtimestep embeddingに加算されて入力されるそうです。

ここまでを踏まえると、VSDのアルゴリズムが完全に理解できると思います。

VSDとSDSの比較

SDSはVSDの特殊系になります。その理由は、VSDで $\mu(\theta | y) \approx \delta(\theta-\theta^{(1)})$ として、 $\theta^{(1)}$ のみの決定的な分布とすると、 $q_t^\mu (x_t|c,y) \approx \mathcal{N}(x_t | \alpha_t g(\theta^{(1)},c), \sigma_t^2 I)$ となり、 $-\sigma_t \nabla_{x_t} \log q_t^\mu (x_t |c,y) \approx (x_t-\alpha_t g(\theta^{(1)},c)) / \sigma_t = \epsilon$ になり、SDSと同じアルゴリズムになります。このことからも、SDSは $\theta$ の点推定をしているのに対し、VSDは $\theta$ の分布を推定していると言うことができます。
またこれにより、VSDはclassifier free guidanceのscaleを7.5という、通常のText-to-Imageモデルと同程度の小さな値で3D生成を可能にしています。これによりSDSが100程度の大きな値が必要で、多様性が失われていた問題を解決しています。
これはSDSは $\epsilon_{\mathrm{pretrain}}(x_t, t, y)$ のみを使うため、 $\epsilon_{\mathrm{pretrain}}(x_t, t, y)$ が十分"sharp"である必要がありましたが、VSDでは $\epsilon_{\mathrm{pretrain}}(x_t, t, y) - \epsilon_\phi(x_t,t,c,y)$ を使うため、この差分が"sharp"であればよく、そのため7.5程度の小さなCFG scaleでも十分になると説明されています。

実験

ProlificDreamerではMagic3Dと同様に、NeRFで学習→DMTetでmeshの学習の2-stageの学習方法を採用しています。NeRF表現としてはInstant NGPを採用し、最初から512x512の高解像度で学習を行います。また、学習初期ではノイズをかける時刻 $t$ を $\mathcal{U(0.02, 0.98)}$ からサンプリングするのに対し、その後は $t \sim \mathcal{U(0.02, 0.50)}$ にして狭めるannealingをしています。これは小さい $t$ の方が自然画像に近く、学習後期の最適化に適しているためです。

定性的なAblation study

このようにして生成された3Dモデルは以下のように超高精細で、各視点画像がStableDiffusionなどで生成した一枚絵に迫るほど綺麗なものになっています。

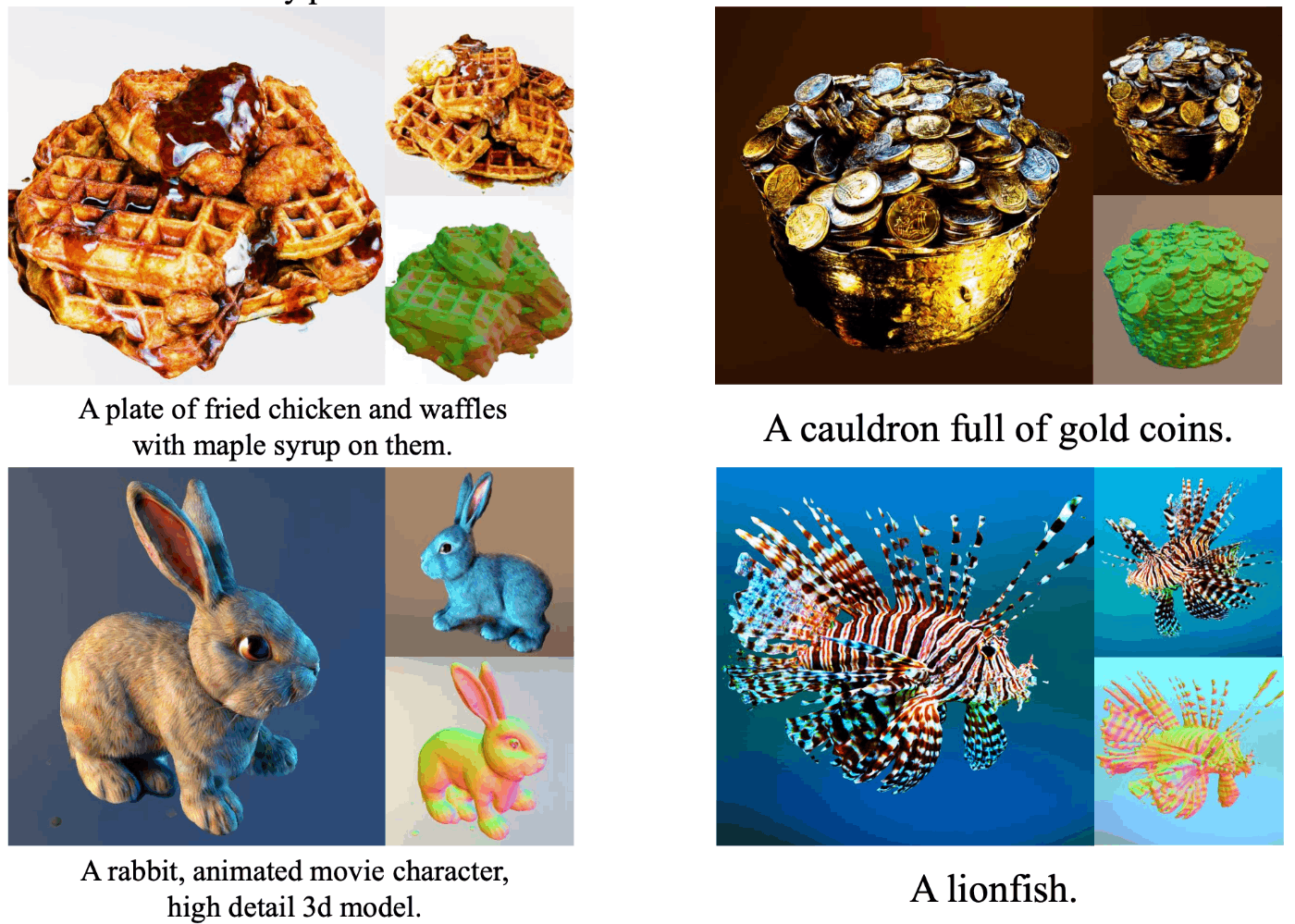
また、一つの入力テキストから多様な3Dモデルが生成され、SDS系の3D生成モデルの欠点を解決していることがわかります。

また論文中ではVSDやSDSを用いて2D画像の生成を行った場合の結果も掲載されています。下図の(a)と(b)はSDSで2D画像を最適化したもの、(c)はDPM-solverで通常通りStableDiffusionから生成した画像、(d)はVSDを使って最適化した2D画像です。VSDではDPM-Solverと同じかそれよりも綺麗な画像が出来上がっていることが驚きです。今後例えばStableDiffusionから生成した画像にVSDを適用してよりクオリティの高い画像にしたり、画像を修正するなどの応用も考えられるかもしれません。

DreamFusionやFantasia3Dとの比較もより詳細に記載されており、格段に高クオリティな3Dモデルが生成できることが見て取れます。

ちょうど同時期（5/19)に発表されたText2NeRFの生成結果を見てみても、（手法が全く異なるので単純な比較はできませんが）Text2NeRFが正面方向の視点や360度視点の生成にフォーカスしており、2D画像を貼り付けていったような3Dシーンが生成されるのに対して、ProlificDreamerはより3次元的に一貫性の取れた生成ができているのではないかと思います。

Text2NeRFの生成結果

ProlificDreamerの生成結果

定量評価としてはUser studyを行っています。既存手法よりも良い結果が得られています。
User studyの他に定量評価として、DreamFusionで行われているようなCLIP R-Precisionの計測があるとより良いと思いますが、定性評価やUser studyをもってProlificDreamerが既存手法よりも良いことは明白と言えると思います。

まとめ

今回はProlificDreamerとその理論的背景のVSDを解説してきました。VSDはこれまで広く使われていたSDSをより一般化し、SDSが抱えていた様々な問題を解決するもので、今後のText-to-3Dモデルの主流になっていく可能性が高いと感じています。とはいえ、この分野は発展が異常なほど早く、明日にはまたさらに良い手法が出てくる可能性があるため確定的なことは言えませんが、少なくともこの手法はこれまでのText-to-3Dの問題を多く解決し、生成クオリティを飛躍的に向上させ、理論的背景を強固なものにしたという点で、貢献度は大きいと思います。すでにthreestudioでは試験的な実装がなされ、公式のgithubでも今後実装が公開されるようなので、今後の発展が期待されます。

参考文献

https://dreamfusion3d.github.io/

https://arxiv.org/abs/2211.07600

https://bluestyle97.github.io/dream3d/
https://fantasia3d.github.io/

https://arxiv.org/abs/2305.02463

https://arxiv.org/abs/2305.16213

https://arxiv.org/abs/2006.11239
https://arxiv.org/abs/2208.11970
https://arxiv.org/abs/2303.17015

https://arxiv.org/abs/2106.09685
https://arxiv.org/abs/2206.00927

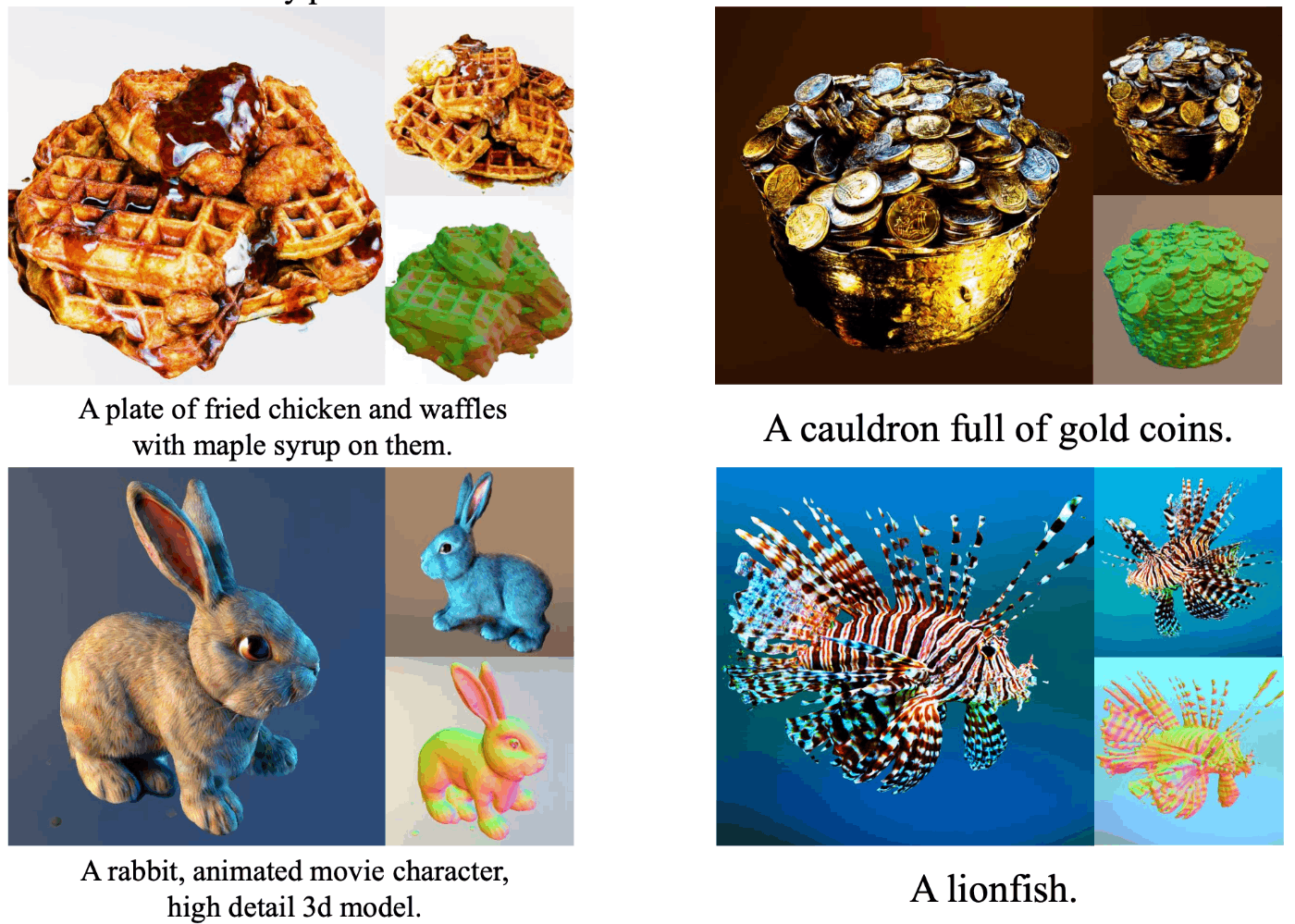
Discussion

ログインするとコメントできます